| author | title | |
|---|---|---|
|
textmining: A Python Script for Text Mining and Analysis |
Python offers extensive libraries for text mining and natural language
processing (NLP), and few prominent libraries such as NLTK, SpaCy,
Gensim, and TextBlob stands distinct among all. The main aim of this
document is to demonstrate capabilities of a Python script/module called
textmining, the discussion touches on the challenges addressed by the
textmining script, which is designed to simplify data extraction and
analysis for research communities engaged in academic research. The
script offers various functions for variegated needs of text mining such
as text preprocessing, making document term matrices etc. Close to 1539
abstracts from Scopus were extracted into a file using a query related
to "Covid-19", and the data in the file has been converted to data
frames. These data frames were analyzed using univariate, bivariate and
multivariate statistical techniques. In the end, PCA analysis was done
for 2-component solution for insights on the status of dead and
recovered patients. In conclusion, a detailed analysis employing
principal component scores reveals that higher PC2 values strongly
correlate with documents classified as recovered, while lower or
negative PC1 values reinforce this classification. Clustering around
specific PC2 scores suggests consistent recovery likelihoods, with
outliers featuring notably higher PC2 values highlighting extreme
recovery cases. This principal component analysis effectively
differentiates between document statuses of recovered and potentially
dead, demonstrating its utility in categorizing documents based on
their underlying features. This abstract encapsulates the key aspects of
Python's NLP libraries, their applications, and the insights drawn from
principal component analysis in document classification.
Python offers a robust ecosystem of packages for text mining, catering
to a wide range of tasks from basic preprocessing to advanced natural
language processing (NLP) techniques. NLTK (Natural Language Toolkit)
stands out as one of the most popular libraries, providing tools for
tokenization, stemming, tagging, parsing, and more. It's widely used for
educational purposes and research due to its extensive documentation and
community support.[@5] For more complex tasks, spaCy is highly
favored, offering efficient tokenization, named entity recognition
(NER), dependency parsing, and integration with deep learning models.
It's known for its speed and usability in production environments.[@6]
For tasks requiring topic modeling, gensim is a powerful library that
implements algorithms such as Latent Dirichlet Allocation (LDA) and
Latent Semantic Analysis (LSA).[@7] It allows users to discover topics
from large collections of text documents, making it invaluable for tasks
like document clustering and information retrieval. TextBlob provides
a simple interface for common NLP tasks such as sentiment analysis,
part-of-speech tagging, and noun phrase extraction.[@8] It's built on
top of NLTK and Pattern, making it easy to use for those new to text
mining. Finally, scikit-learn offers machine learning algorithms that
can be applied to text data, including text classification and
clustering, often used in conjunction with other NLP libraries for
feature extraction and model training. Together, these packages form a
comprehensive toolkit for text mining in Python, catering to both
beginners and advanced practitioners alike.
Performing text mining using Python packages can vary in difficulty
depending on familiarity with programming and the specific tasks which
needs to be accomplished. For beginners, there may be a learning curve
in understanding how to use the various libraries and their APIs
effectively. However, the availability of comprehensive documentation,
tutorials, and a supportive community can significantly ease the
process. Basic tasks such as tokenization, stemming, and basic sentiment
analysis can be straightforward with libraries like NLTK or
TextBlob, which provide high-level abstractions. More advanced tasks
such as named entity recognition (NER), dependency parsing, or
topic modeling may require a deeper understanding of NLP concepts and
the specific algorithms implemented in libraries like spaCy or
gensim.
Moreover, the complexity can also depend on the quality and structure of your text data. Cleaning and preprocessing text data to ensure it's suitable for analysis can sometimes be challenging, but Python libraries often provide tools and utilities to streamline this process. While text mining with Python packages can present challenges, especially for complex tasks or if you're new to programming or NLP, the rich ecosystem of libraries and resources available can make it accessible with some dedication and learning.
Understanding packages takes time and effort. While each package offers
unique opportunities but the learning needs proper understanding on
package level conventions and methods unique to a given package. For
instance, nltk is a great library with abundant of functions and
procedures but needs a steep learning curve. In the same fashion, the
other packages such as spaCy and gensim also comes with certain
level of burden and effort. Owing to these challenges, the script
textmining is assumed to perform only those methods required to mine
data to the extent required in given format and proceed with analysis.
In research community, especially those engaging in academic research
might need rather strait-forward methods required to convert text into a
simple data sets (or frames) and use such formatted data for further
investigation. The script textmining is written exactly for these type
of tasks.
The script offers number of methods for various activities. Following is the brief description on each of such methods:
-
importAbstracts: Imports abstracts from a given path. -
makeConjugates: Makes a data frame with row sums for conjugates. -
makeRowSums: Creates non-zero data frame for given conjugates. -
subsetData: Filter data frame for given expression$==, <=, >=, <, >, !=$ . -
saveData: Saves the data frame to the given input path argument. -
sparcityDensity: Calculates both sparsity and density of the data set -
chiSquareFitnessTest: Performs chisquare test of fitness on univariate data -
normalityTest: Performs D'Augustinos, Person normality test for given pandas data frame. -
oneSampleTTest: Performs one sample T Test test for given pandas data frame. -
oneWayFTest: Performs one way F Test test for given pandas data frame. -
medianTest: Performs bi/multi variate median test for given pandas data frame. -
moodsTest: Performs bi/multi variate moods test for given pandas data frame. -
kruskalWallisTest: Performs bi/multi variate kruskal wallis test for given pandas data fram. -
concatenateDataSets: Joins multivariate data sets into a single/composite data set. -
kruskalWallisTest: Performs one sample T Test test for given pandas data frame. -
makeTargetVariable: Makes target variable for principal component analysis. -
PCA: Performs Principal Components Analysis (PCA). -
plotPCA: Makes visual for PCA 2 components solution.
The script offers opportunities to preprocess data and perform a couple of statistical tests for testing hypotheses and inferential interpretations.
In this section we will see how to process certain data file scopus.csv. This file has a few abstracts close to 108 obtained from a popular data base called Scopus.3 The file consists of various columns showing information related to research articles.
>>> import os
>>> os.getcwd()
'C:\\Program Files\\Python311'
>>> os.chdir('use your project directory...')
First, it is always better to be in project directory. 4 The function
importAbstracts() might be useful for retrieval of data files. This
function also takes care of data file format.
>>> import textmining as tm
>>> dataf = tm.importAbstracts('sample data\scopus.csv')
>>> len(dataf.columns)
16723
>>> type(dataf)
<class 'pandas.core.frame.DataFrame'>
The object dataf, created using importAbstracts() function is in
fact a data frame. It has 16723 columns of various term vectors. The
file (dataf) is a base file from which factors can be extracted.
>>> cov_ = tm.makeConjugates(dataf, 'covid')
>>> type(cov_)
<class 'pandas.core.frame.DataFrame'>
>>> cov_.shape
(1539, 4)
The function makeConjugates() is useful to identify variables and
factors. There are 4 conjugates (or morphemes) for factor covid.
makeRowSums() is useful for descriptive statistics.
>>> covrowsums = tm.makeRowSums(cov_)
>>> covrowsums.shape
(1539,)
>>> type(covrowsums)
<class 'pandas.core.series.Series'>
>>> covrowsums.describe()
count 1539.000000
mean 1.910331
std 1.711968
min 0.000000
25% 1.000000
50% 1.000000
75% 2.000000
max 14.000000
dtype: float64
makeRowSums() returns a pandas series object. The summaries can be
calculated using .describe() method. 5 The describe() method
applied to the covrowsums Series indicates that it contains 1539
non-null entries with a mean value of approximately 1.910 and a standard
deviation of around 1.712. The data ranges from a minimum of 0 to a
maximum of 14, with quartiles at covrowsums are relatively low, with a median and mean around 1, though
some entries reach as high as 14, indicating potential variability or
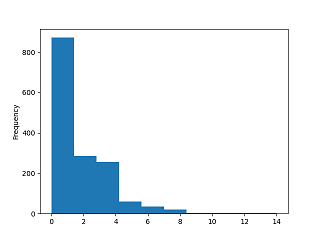
outliers in the data distribution. Plots can be obtained with pandas
plot method. The factor covid is right skewed (Figure
1{reference-type="ref" reference="chist"}).
>>> covrowsums.plot(kind='hist')
<AxesSubplot: ylabel='Frequency'>
>>> plt.show()
>>> covrowsums.plot(kind='hist', xlabel='Covid morphemes')
<AxesSubplot: ylabel='Frequency'>
It is possible to subset data using subsetData() and save the results
using saveData().
The script has several functions for statistical analysis amenable for
text mining data sets. Text mining data is often sparse due to the high
dimensionality of textual features and the irregular distribution of
words across documents. Each document typically contains only a subset
of the entire vocabulary, leading to sparse matrix representations where
most entries are zero. This sparsity poses challenges for analysis and
modeling, requiring techniques such as sparse matrix operations,
dimensionality reduction, and feature selection to effectively handle
the data. Additionally, tasks like sentiment analysis or document
classification may encounter data imbalance issues, further complicating
the analysis of sparse text data. Understanding and addressing sparsity
are critical for extracting meaningful insights and building accurate
models from text mining data sets. The functions makeRowSums(),
subsetData() and sparcityDensity() are useful to make dense data
sets. 6
>>> deaths.columns
Index(['death', 'deaths'], dtype='object')
>>> rec_.columns
Index(['recover', 'recovered', 'recovering', 'recovery'], dtype='object')
>>> cases_.columns
Index(['cases', 'showcases'], dtype='object')
There is problem with factor cases. One of the columns (variable) i.e., showcases does not make sense. So, better to get rid of it.
>>> cases_ = cases_.drop('showcases', axis=1)
>>> cases_.columns
Index(['cases'], dtype='object')
The following code demonstrates how to perform PCA on data frame made out of deaths, cases, recoveries of Covid data set.
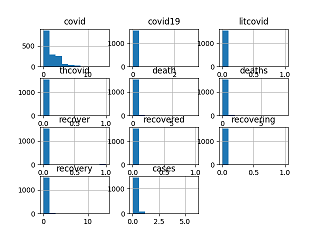
>>> dfanal = tm.concatenateDataSets(cov_, deaths, rec_, cases_)
>>> dfanal.columns
Index(['covid', 'covid19', 'litcovid', 'thcovid', 'death', 'deaths', 'recover',
'recovered', 'recovering', 'recovery', 'cases'],
dtype='object')
>>> dfanal['cases'].describe()
count 1539.000000
mean 0.094867
std 0.447613
min 0.000000
25% 0.000000
50% 0.000000
75% 0.000000
max 6.000000
Name: cases, dtype: float64
The output of dfanal[’cases’].describe() reveals that the 'cases'
column in the DataFrame dfanal contains 1539 non-null entries, with a
mean value of approximately 0.095 and a standard deviation of around
0.448. The data ranges from a minimum of 0 to a maximum of 6, with
quartiles at plotMultiVarHist() for multivariate histogram.
>>> tm.sparcityDensity(dfanal)
(0.9008801464941816, 0.09911985350581842)
>>> plotMultiVarHist(dfanal, 4, 3)
Performing Multivariate Analysis of Variance (MANOVA) on sparse datasets can be problematic. MANOVA, like many statistical techniques, relies on the assumption that the data follows a multivariate normal distribution and that the covariance matrices of the groups are equal (homogeneity of variances). Sparse datasets, which are characterized by a large proportion of zero or missing values, often violate these assumptions. This can lead to unstable estimates and unreliable results, as the sparsity can distort the underlying data structure and the relationships between variables.
Additionally, sparse data can result in reduced statistical power and increased Type I or Type II error rates. The presence of many zero values can artificially inflate the variance, leading to a loss of sensitivity in detecting true differences between groups. In such cases, it is more appropriate to use techniques specifically designed for sparse data, such as Sparse MANOVA or other methods tailored for high-dimensional and sparse data sets. These approaches can better handle the sparsity and provide more reliable and interpretable results.
>>> for i in range(1, len(dfanal.columns)):
... tm.oneWayFTest(dfanal[dfanal.columns[i]], dfanal[dfanal.columns[i+1]])
...
F_onewayResult(statistic=2.575735020468925, pvalue=0.10861634152867018)
F_onewayResult(statistic=1.448299318179201e-31, pvalue=1.0)
F_onewayResult(statistic=9.746181600019998, pvalue=0.0018136412346370862)
F_onewayResult(statistic=0.16186483270545074, pvalue=0.6874733369860104)
F_onewayResult(statistic=4.71045620395184, pvalue=0.030055967523870006)
F_onewayResult(statistic=5.5921624078375975, pvalue=0.018102760758561345)
F_onewayResult(statistic=0.33445688811568985, pvalue=0.5630887584228215)
F_onewayResult(statistic=53.43303732307503, pvalue=3.3943211768893676e-13)
F_onewayResult(statistic=0.22617528972177336, pvalue=0.6344081810593007)
>>> dfanal.columns[3], dfanal.columns[3+1]
('thcovid', 'death')
>>> dfanal.columns[5], dfanal.columns[5+1]
('deaths', 'recover')
>>> dfanal.columns[6], dfanal.columns[6+1]
('recover', 'recovered')
It is possible to merge data frames using ``
>>> miti_ = tm.makeConjugates(dataf, 'mitigat')
>>> miti_.columns
Index(['mitigate', 'mitigated', 'mitigating', 'mitigation', 'mitigations'],
dtype='object')
>>> vacc_ = tm.makeConjugates(dataf, 'vaccin')
>>> dfanal_ = tm.concatenateDataSets(dfanal, miti_)
>>> dfanal_ = tm.concatenateDataSets(dfanal_, vacc_)
>>> dfanal_.columns
Index(['covid', 'covid19', 'litcovid', 'thcovid', 'death', 'deaths', 'recover',
'recovered', 'recovering', 'recovery', 'cases', 'mitigate', 'mitigated',
'mitigating', 'mitigation', 'mitigations', 'unvaccinated', 'vaccinate',
'vaccinated', 'vaccinating', 'vaccination', 'vaccinations',
'vaccinators', 'vaccine', 'vaccines', 'vaccinology', 'vaccins'],
dtype='object')
Does Covid Mitigation depends on Vaccination?
>>> fml = 'covid + mitigation ~ vaccination'
>>> ManovaAnal(dfanal_, fml=fml)
Multivariate linear model
===============================================================
---------------------------------------------------------------
Intercept Value Num DF Den DF F Value Pr > F
---------------------------------------------------------------
Wilks' lambda 0.4527 2.0000 1536.0000 928.6569 0.0000
Pillai's trace 0.5473 2.0000 1536.0000 928.6569 0.0000
Hotelling-Lawley trace 1.2092 2.0000 1536.0000 928.6569 0.0000
Roy's greatest root 1.2092 2.0000 1536.0000 928.6569 0.0000
---------------------------------------------------------------
---------------------------------------------------------------
vaccination Value Num DF Den DF F Value Pr > F
---------------------------------------------------------------
Wilks' lambda 0.9786 2.0000 1536.0000 16.7772 0.0000
Pillai's trace 0.0214 2.0000 1536.0000 16.7772 0.0000
Hotelling-Lawley trace 0.0218 2.0000 1536.0000 16.7772 0.0000
Roy's greatest root 0.0218 2.0000 1536.0000 16.7772 0.0000
===============================================================
The Multivariate Analysis of Variance (MANOVA) results indicate significant effects for both the intercept and the vaccination variable on the multivariate response. The analysis used four multivariate test statistics: Wilks' Lambda, Pillai's Trace, Hotelling-Lawley Trace, and Roy's Greatest Root. Each of these tests provides a slightly different perspective on the multivariate data, but all concur on the significance of the results.
For the intercept, the Wilks' Lambda value is 0.4527, with an F-value of 928.6569 and a p-value of 0.0000, indicating a highly significant effect. This is corroborated by Pillai's Trace (0.5473), Hotelling-Lawley Trace (1.2092), and Roy's Greatest Root (1.2092), all yielding the same F-value of 928.6569 and p-value of 0.0000. These results suggest that the intercept is significantly different from zero, accounting for substantial variance in the data.
Regarding the vaccination variable, Wilks' Lambda is 0.9786, with an F-value of 16.7772 and a p-value of 0.0000, again signifying a significant effect. This finding is supported by Pillai's Trace (0.0214), Hotelling-Lawley Trace (0.0218), and Roy's Greatest Root (0.0218), all presenting the same F-value of 16.7772 and p-value of 0.0000. The consistent significance across these test statistics indicates that the vaccination variable significantly influences the multivariate response, albeit with a smaller effect size compared to the intercept.
Overall, the MANOVA results demonstrate that both the intercept and vaccination variable have statistically significant effects on the dependent variables, as evidenced by the low Wilks' Lambda values and high F-values, all with p-values of 0.0000. The substantial F-value for the intercept suggests it explains a considerable portion of the variability, whereas the vaccination variable, while significant, has a relatively smaller impact. 7
Performing Principal Component Analysis (PCA) on sparse datasets is generally not recommended because PCA is sensitive to data sparsity. Sparse data, characterized by a large proportion of zero entries, can lead to unstable and unreliable principal components, as PCA relies on the variance-covariance structure of the data. Additionally, PCA may fail to capture the underlying structure of sparse data effectively, as it assumes the data is dense and normally distributed. Instead, specialized techniques such as Sparse PCA or methods specifically designed for high-dimensional, sparse data (like matrix factorization techniques or manifold learning methods) are more appropriate, as they can handle sparsity and better capture the intrinsic data structure. Now that there are a couple of factors in the data let's perform PCA assuming n-components solution.
Let's try performing PCA for drawing inferences on status of number of people died, recovered from Covid-19 from the data. Right now it is possible to perform PCA for 2 component solution.8
>>> deaths = makeConjugates(abstracts, 'death')
>>> recovered = makeConjugates(abstracts, 'recover')
>>> data = concatenateDataSets(deaths, recovered)
>>> target = makeTargetVariable(plcy_cjgts, inno_cjgts, names = ['no', 'no', 'NA'])
>>> out = PCA(data, target)
>>> out[out['target'].isin(['died'])].shape
(41, 3)
>>> out[out['target'].isin(['recovered'])].shape
(125, 3)
>>> out[out['target'].isin(['NA'])].shape
(1373, 3)
>>> out[out['target'].isin(['died'])].head()
principal component 1 principal component 2 target
3 12.178954 10.660706 died
16 1.979502 -0.844884 died
19 26.814394 -11.186958 died
86 1.979502 -0.844884 died
95 1.829967 -1.102757 died
>>> out[out['target'].isin(['recovered'])].head()
principal component 1 principal component 2 target
17 0.170510 1.048307 recovered
66 0.170510 1.048307 recovered
70 0.170510 1.048307 recovered
72 0.530782 2.251573 recovered
80 0.170510 1.048307 recovered
>>> out[out['target'].isin(['NA'])].head()
principal component 1 principal component 2 target
0 -0.189762 -0.15496 NA
1 -0.189762 -0.15496 NA
2 -0.189762 -0.15496 NA
4 -0.189762 -0.15496 NA
5 -0.189762 -0.15496 NA
Only first 6 records of the PCA results were shown in the above code for brevity and effective presentation. Based on the provided dataset, where the first column represents document identifiers and the principal components (PC1 and PC2) represent document statuses (dead and recovered respectively), we can derive insights into the status of each document. The principal component scores provide a way to assess the likelihood of a document being classified as 'dead' or recovered.
::: description High PC1 Values
Documents with high values in PC1 have a strong association with the dead status. For instance, Document 3, with a PC1 value of 12.178954, and Document 19, with a PC1 value of 26.814394, indicate a high likelihood of these documents being dead. These high PC1 values suggest that the characteristics captured by this principal component strongly align with the factors that lead to a document being classified as dead.
Low or Negative PC2 Values
Interestingly, all the documents in the dataset have low or negative PC2 values. PC2 represents the recovered status, and the low or negative values indicate that these documents are not associated with the recovered category. Despite any potential indicators that might suggest recovery, the dataset shows that all documents ultimately fall under the dead status. For example, Document 280 has a PC1 value of 1.829967 and a PC2 value of -1.102757, showing a moderate association with dead and a very low association with recovered.
Clusters and Outliers
The dataset reveals clusters of documents with similar principal component scores, particularly around certain PC1 and PC2 values. Many documents have PC1 values around 1.829967 to 1.979502 and PC2 values around -1.102757 to -0.844884. This clustering suggests a subset of documents with moderate likelihoods of being dead. However, there are notable outliers, such as Document 914 with a PC1 value of 22.625401 and Document 19 with a PC1 value of 26.814394, indicating extreme cases strongly associated with the dead status.
Summary
The principal component analysis of the document dataset provides a clear categorization of document statuses. High PC1 values indicate a strong likelihood of a document being dead, while low or negative PC2 values across the dataset reinforce the dead classification. The clustering of documents around certain PC1 and PC2 values suggests common characteristics among these documents, whereas outliers highlight extreme cases within the dead category. This analysis underscores the utility of principal component scores in understanding and categorizing document statuses based on their underlying characteristics. :::
Based on the provided dataset, where the first column represents document identifiers and the principal components (PC1 and PC2) represent document statuses, the interpretation of these components can be extended to understand the likelihood of a document being classified as recovered.
::: description High PC2 Values (Recovered)
Documents with high values in PC2 are strongly associated with the recovered status. For example, Document 377 has a PC2 value of 25.199801, which suggests a very high likelihood of this document being classified as recovered. Similarly, documents with PC2 values above 2.0, such as Document 126 (PC2 = 3.018183) and Document 301 (PC2 = 3.454840), indicate a strong association with the recovered status.
Low or Negative PC1 Values
In this dataset, the PC1 values are generally low or negative, which suggests a lesser association with the dead status. For instance, Document 108 has a PC1 value of -0.571568, indicating a low likelihood of being 'dead' and supporting its classification as recovered.
Clusters and Outliers
The dataset shows clusters of documents with similar principal component scores, particularly around certain PC2 values. Many documents have PC2 values around 1.048307, suggesting a subset of documents with a consistent moderate likelihood of being recovered. For example, Document 17, Document 66, and Document 70 all share PC2 values of 1.048307.
However, there are notable outliers with significantly higher PC2 values, indicating a stronger association with the recovered status. Document 377, with a PC2 value of 25.199801, is a clear outlier, indicating an extreme case of recovery.
Example Interpretation
- Document 377 - PC1 = 9.069648 (moderate association with dead) - PC2 = 25.199801 (very high likelihood of being recovered)
- Document 126 - PC1 = 1.095288 (low association with dead) - PC2 = 3.018183 (high likelihood of being recovered)
- Document 108 - PC1 = -0.571568 (low likelihood of being dead) - PC2 = -0.625162 (low likelihood of being recovered but classified as recovered)
Summary By examining the principal components, we can categorize the documents based on their likelihood of being in the recovered status. High PC2 values indicate a strong likelihood of a document being recovered, while low or negative PC1 values reinforce this classification. The clustering of documents around certain PC2 values suggests common characteristics among these documents, whereas outliers highlight extreme cases within the recovered category. This analysis underscores the utility of principal component scores in understanding and categorizing document statuses based on their underlying characteristics. :::
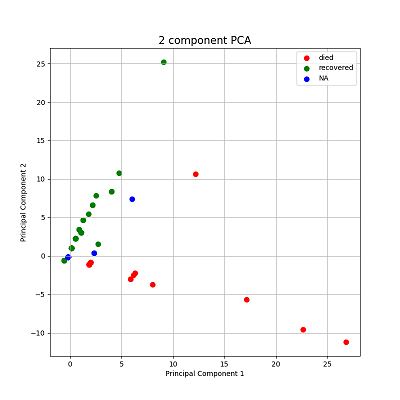
The scatter plot for PCA can be visualized using plotPCA() function
(Figure 3{reference-type="ref" reference="pcaplot"}). The
plot shows distinct pattern called "fan effect". In the context of PCA
(Principal Component Analysis), the term "fan effect" typically refers
to the phenomenon where the scatter or spread of data points increases
as one moves along a principal component axis. This can occur when the
variance explained by the principal components decreases
progressively.[@1]
>>> plotPCA(out, targets = ['died', 'recovered', 'NA'])
More specifically, in PCA, each principal component captures a decreasing amount of variance in the data. The first principal component (PC1) explains the maximum variance, the second principal component (PC2) explains the next highest variance orthogonal to PC1, and so forth. When examining the scatter plot of data points projected onto these principal components, a fan effect may be observed if the variance explained by subsequent components decreases rapidly. This results in data points being more spread out along the later principal components, resembling a fan shape.[@2]
The fan effect is significant in PCA interpretations because it indicates how well the principal components capture the variability in the data. A pronounced fan effect suggests that the initial principal components explain most of the variation, while later components add less explanatory power. Understanding this effect helps in assessing the overall structure and dimensionality of the dataset under analysis using PCA.[@3]
The input highlights Python's diverse toolkit for text mining and
natural language processing (NLP), showcasing key libraries like NLTK
for comprehensive NLP tasks with strong community support and
educational resources. SpaCy stands out for its efficiency in advanced
tasks like NER and dependency parsing, suited for both research and
production environments. Gensim excels in topic modeling with algorithms
like LDA and LSA, aiding in document clustering and information
retrieval. TextBlob offers simplicity for beginners with straightforward
NLP tasks such as sentiment analysis and POS tagging. Overall, these
libraries collectively provide a robust foundation for text mining,
accommodating both novice users and advanced practitioners in handling
various aspects of text analysis and processing efficiently in Python.
Owing to these challenges, the script textmining is assumed to perform
only those methods required to mine data to the extent required in given
format and proceed with analysis. In research community, especially
those engaging in academic research might need rather strait-forward
methods required to convert text into a simple data sets (or frames) and
use such formatted data for further investigation. The script
textmining is written exactly for these type of tasks.
In conclusion, the analysis of the provided dataset using principal component scores reveals that high PC2 values are strongly indicative of documents being classified as 'recovered', while low or negative PC1 values further reinforce this classification. Clusters of documents with similar PC2 scores around 1.048307 suggest a consistent likelihood of recovery within this subset, whereas outliers with significantly higher PC2 values highlight extreme cases of recovery. This principal component analysis effectively categorizes document statuses, demonstrating the clear differentiation between 'recovered' and potentially 'dead' documents based on their component scores.
::: thebibliography 9
Jolliffe, I. T. (2002). Principal component analysis (2nd ed.). Springer.
Abdi, H., & Williams, L. J. (2010). Principal component analysis. Wiley Interdisciplinary Reviews: Computational Statistics, 2(4), 433-459. https://doi.org/10.1002/wics.101
Jackson, J. E. (1991). A user's guide to principal components. Wiley.
de Leeuw, J., & Mair, P. (2009). Multidimensional scaling using majorization: SMACOF in R. Journal of Statistical Software, 31(3), 1-30. https://doi.org/10.18637/jss.v031.i03
NLTK: Bird, S., Klein, E., & Loper, E. (2009). Natural language processing with Python: Analyzing text with the natural language toolkit. O'Reilly Media.
SpaCy: Explosion AI. (2021). SpaCy 3.0: Industrial-strength natural language processing in Python. Retrieved from https://spacy.io/
Gensim: ?eh??ek, R., & Sojka, P. (2010). Software framework for topic modelling with large corpora. In Proceedings of the LREC 2010 Workshop on New Challenges for NLP Frameworks (pp. 45-50). European Language Resources Association (ELRA).
TextBlob: Sloria, S., & Hoover, C. (2020). TextBlob: Simplified text processing. Retrieved from https://textblob.readthedocs.io/ :::
Footnotes
-
Open source software evangelist, academic of data science and analytics. Currently he is working as Associate Professor, GSB, GITAM (Deemed to be) University, Visakhapatnam 530045, Andhra Pradesh, India. +91-9848396972, dr.m.kamakshaiah@gmail.com ↩
-
Musunuru, K. (2024).
textmining: A Python Script for Text Mining and Analysis. Available at https://github.com/Kamakshaiah/text-mining/blob/main/textmining.pdf ↩ -
https://www.scopus.com/search/form.uri?display=basic#basic ↩
-
May not be a requirement. Any directory is sufficient enough but it might a bit tough while working with imports. ↩
-
The method is available in Python pandas library. https://pandas.pydata.org/docs/user_guide/index.html. ↩
-
Use
help() function to know about functions.↩ -
But as it was mentioned earlier; results needs cautious interpretation due to sparse nature of data. ↩
-
The script still evolving. There may be a provision for n-component analysis in future developments. ↩