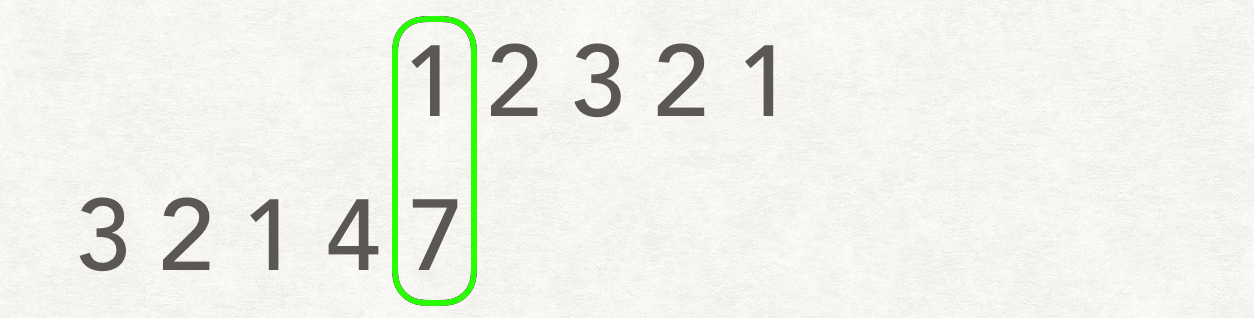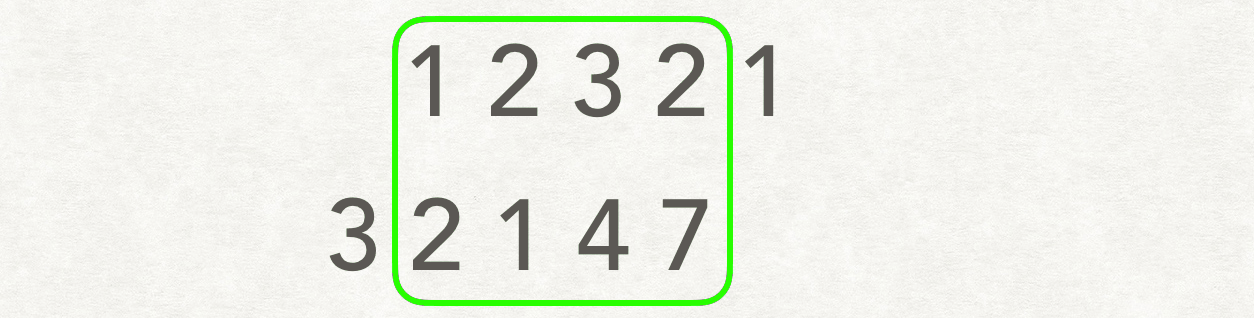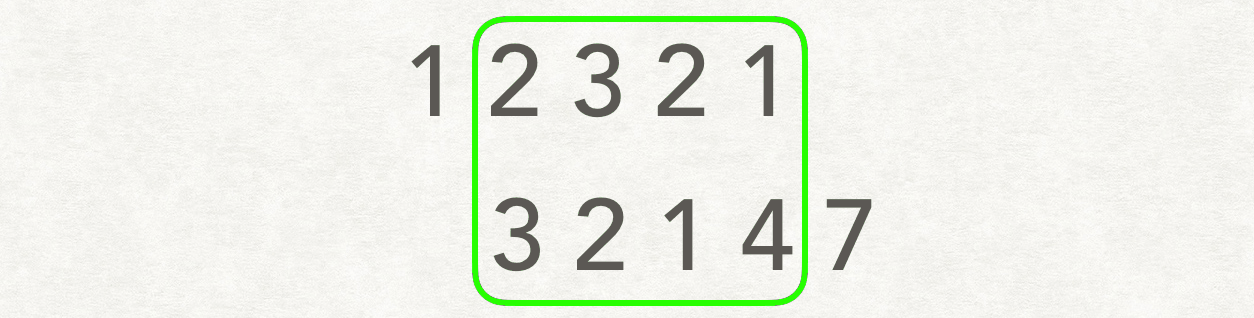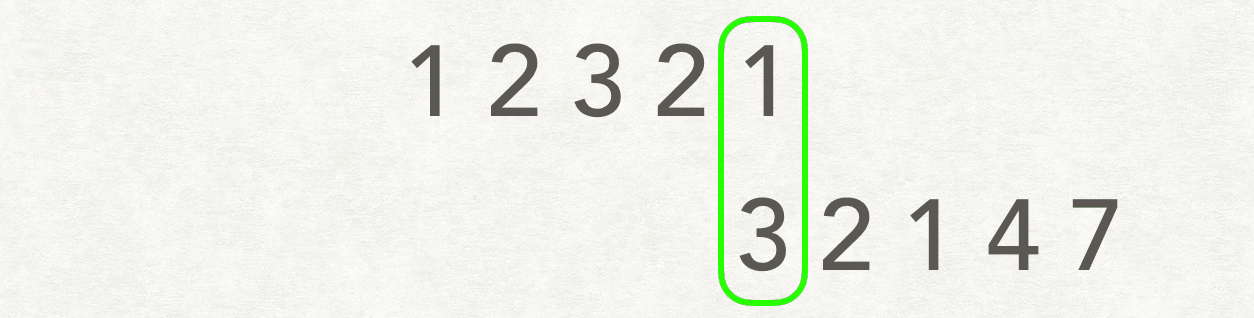001-两数之和/167. 两数之和 II - 输入有序数组
一者遍历,一者通过hash表(字典数据),hash表所花时间反而更长?
# 28ms
class Solution(object):
def twoSum(self, nums, target):
dic = dict()
for i, num in enumerate(nums):
if target - num in dic:
return [dic[target - num], i]
dic[nums[i]] = i
return [] 给定一个已按照 升序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ,所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例 1:
输入:numbers = [2,7,11,15], target = 9 输出:[1,2] 解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
L, R = 0, len(numbers)-1
while L < R:
if numbers[L] + numbers[R] == target:
return [L+1, R+1]
elif numbers[L] + numbers[R] > target:
R -= 1
else:
L += 1给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和。
提示:
num1 和num2 的长度都小于 5100 num1 和num2 都只包含数字 0-9 num1 和num2 都不包含任何前导零 你不能使用任何內建 BigInteger 库, 也不能直接将输入的字符串转换为整数形式
大数相加:
class Solution(object):
def addStrings(self, num1, num2):
"""
:type num1: str
:type num2: str
:rtype: str
"""
# 返回值,是否有进位,从个位数开始计算
res, carry, i, j = '', 0, len(num1)-1, len(num2)-1
while 0<=i or 0<=j:
n1 = int(num1[i]) if 0<=i else 0
n2 = int(num2[j]) if 0<=j else 0
res = str((n1+n2+carry)%10) + res # 计算相加后个位值
carry = (n1+n2+carry)//10 # 判断是否有进位
i -= 1 # 两指针依次移动
j -= 1
return '1'+res if carry else res给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:

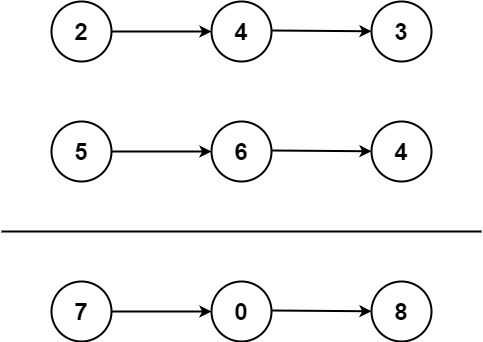
输入:l1 = [2,4,3], l2 = [5,6,4] 输出:[7,0,8] 解释:342 + 465 = 807.
与上一题一样:
class Solution(object):
def addTwoNumbers(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
res, carry = ListNode(), 0
tmp = res
while l1 or l2:
n1 = l1.val if l1 else 0
n2 = l2.val if l2 else 0
tmp.next = ListNode((n1+n2+carry)%10)
carry = (n1+n2+carry)//10
tmp = tmp.next
if l1: l1 = l1.next
if l2: l2 = l2.next
if carry: tmp.next = ListNode(carry)
return res.next假设链表中每一个节点的值都在 0 - 9 之间,那么链表整体就可以代表一个整数。
给定两个这种链表,请生成代表两个整数相加值的结果链表。
例如:链表 1 为 9->3->7,链表 2 为 6->3,最后生成新的结果链表为 1->0->0->0。
输入:
[9,3,7],[6,3]返回值:
{1,0,0,0}
与上一题一样,只是正向表示数值,用列表存储数值,后正常计算,再反向输出:
class Solution:
def addInList(self , head1 , head2 ):
# write code here
l1, l2, carry, res, ans = [], [], 0, [], ListNode(0)
while head1:
l1.append(head1.val)
head1 = head1.next
while head2:
l2.append(head2.val)
head2 = head2.next
while l1 or l2:
n1 = l1.pop() if l1 else 0
n2 = l2.pop() if l2 else 0
res.append((n1+n2+carry)%10)
carry = (n1+n2+carry)//10
if carry: res.append(carry)
tmp = ans
while res:
tmp.next = ListNode(res.pop())
tmp = tmp.next
return ans.next给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
示例 1:
输入: num1 = "2", num2 = "3" 输出: "6" 示例 2:
输入: num1 = "123", num2 = "456" 输出: "56088" 说明:
- num1 和 num2 的长度小于110。
- num1 和 num2 只包含数字 0-9。
- num1 和 num2 均不以零开头,除非是数字 0 本身。
- 不能使用任何标准库的大数类型(比如 BigInteger)或直接将输入转换为整数来处理。
'''
num1的第i位(高位从0开始)和num2的第j位相乘的结果在乘积中的位置是[i+j, i+j+1]
例: 123 * 45, 123的第1位 2 和45的第0位 4 乘积 08 存放在结果的第[1, 2]位中
index: 0 1 2 3 4
1 2 3
* 4 5
---------
1 5
1 0
0 5
---------
0 6 1 5
1 2
0 8
0 4
---------
0 5 5 3 5
这样我们就可以单独都对每一位进行相乘计算把结果存入相应的index中
'''
class Solution(object):
def multiply(self, num1, num2):
res = 0
for i in range(1,len(num1)+1):
for j in range(1, len(num2)+1):
res += int(num1[-i]) * int(num2[-j]) *10**(i+j-2)
return str(res)
class Solution(object):
def multiply(self, num1, num2):
num1_len = len(num1)
num2_len = len(num2)
res = [0] * (num1_len + num2_len)
for i in range(num1_len-1, -1, -1):
for j in range(num2_len-1, -1, -1):
tmp = int(num1[i]) * int(num2[j]) + int(res[i+j+1])
res[i+j+1] = tmp%10 # 余数作为当前位
res[i+j] = res[i+j] + tmp//10 # 前一位加上,进位(商作为进位)
res = list(map(str, res))
for i in range(num1_len+num2_len):
if res[i]!='0': # 找到第一个非0数字,后面就是结果
return ''.join(res[i:])
return '0'对于非负整数 X 而言,X 的数组形式是每位数字按从左到右的顺序形成的数组。例如,如果 X = 1231,那么其数组形式为 [1,2,3,1]。
给定非负整数 X 的数组形式 A,返回整数 X+K 的数组形式。
示例 1:
输入:A = [1,2,0,0], K = 34 输出:[1,2,3,4] 解释:1200 + 34 = 1234
class Solution(object):
def addToArrayForm(self, num, k):
"""
:type num: List[int]
:type k: int
:rtype: List[int]
"""
res= 0
for it in num:
res = 10*res+it
res += k
return [int(it) for it in str(res)]
class Solution:
def addToArrayForm(self, A, K):
return list(map(int, str(int(''.join(map(str, A)))+K)))给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
示例 1:
输入:nums = [2,0,2,1,1,0] 输出:[0,0,1,1,2,2]
# 最简单为sort
class Solution(object):
def sortColors(self, nums):
return nums.sort()双指针:
class Solution(object):
def sortColors(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
start, end, i = 0, len(nums)-1, 0
while i <= end:
if nums[i] == 0: # 为0时,与前端交换
nums[i], nums[start] = nums[start], 0
start += 1
elif nums[i] == 2: # 为2时,与末端交换
nums[i], nums[end] = nums[end], 2
end -= 1
i -= 1
i += 1
return nums输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
示例:
输入:nums = [1,2,3,4] 输出:[1,3,2,4] 注:[3,1,2,4] 也是正确的答案之一。
class Solution:
def exchange(self, nums: List[int]) -> List[int]:
start, end, i = 0, len(nums)-1, 0
while i <= end:
if nums[i]%2 == 1: # 为0时,与前端交换
nums[i], nums[start] = nums[start], nums[i]
start += 1
elif nums[i]%2 == 0: # 为2时,与末端交换
nums[i], nums[end] = nums[end], nums[i]
end -= 1
i -= 1
i += 1
return nums给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12] 输出: [1,3,12,0,0] 说明:
必须在原数组上操作,不能拷贝额外的数组。 尽量减少操作次数。
如上题:
class Solution:
def moveZeroes(self, nums):
"""
Do not return anything, modify nums in-place instead.
"""
end, i = len(nums)-1, 0
while i <= end:
if nums[i] == 0:
nums.pop(i)
nums.append(0)
end -= 1
i -= 1
i += 1
return nums给定一个整数数组和一个整数 k,你需要找到该数组中和为 k 的连续的子数组的个数。
示例 1 :
输入:nums = [1,1,1], k = 2 输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。
前缀和**:求数列的和时,Sn = a1+a2+a3+...an; 此时Sn就是数列的前n项和。例S5 = a1 + a2 + a3 + a4 + a5; S2 = a1 + a2,即可以通过 S5-S2 得到 a3+a4+a5 的值。
# 字典数存储,并优化
class Solution(object):
def subarraySum(self, nums, k):
Sum, res, cul = 0, 0, {}
cul[0] = 1
for i in range(len(nums)):
Sum += nums[i]
if Sum - k in cul: # 查找k的倍数,如果存在,加1,
res += cul[Sum-k]
if Sum not in cul: # 保存前缀和
cul[Sum] = 0
cul[Sum] += 1
return res 为什么我们只要查看是否含有 presum - k ,并获取到presum - k 出现的次数就行呢?见下图,所以我们完全可以通过 presum - k的个数获得 k 的个数
给定一个数组 nums 和一个目标值 k,找到和等于 k 的最长子数组长度。如果不存在任意一个符合要求的子数组,则返回 0。
示例 1: 输入: nums = [1, -1, 5, -2, 3], k = 3 输出: 4
在上一题的基础上,存储索引即可。
class Solution(object):
def maxSubArrayLen(self, nums, k):
Sum, cul, res = 0, {}, 0
cul[0] = -1 # 余数为0时,索引为-1,以免第一次遇见可整除时,满足条件
for i in range(len(nums)):
Sum += nums[i]
if Sum - k in cul: # 查找k的倍数,如果存在,加1,
res = max(res, i - cul[Sum-k])
if Sum not in cul: # 保存前缀和
cul[Sum] = i # 存储索引
return res给定一个整数数组 A,返回其中元素之和可被 K 整除的(连续、非空)子数组的数目。
示例:
输入:A = [4,5,0,-2,-3,1], K = 5 输出:7 解释: 有 7 个子数组满足其元素之和可被 K = 5 整除: [4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
(presum[j+1] - presum[i] ) % k是满足条件,可变为presum[j +1] % k = presum[i] % k,余数相同则计算。
class Solution(object):
def subarraysDivByK(self, nums, k):
Sum, res, cul = 0, 0, {}
cul[0] = 1
for i in range(len(nums)):
Sum += nums[i] # 前缀和
key = (Sum % k + k) % k # 获得整除的余数,加k的目的是,当被除数为负数时取模结果为负数,需要纠正
if key in cul: # 如果存在,加1
res += cul[key]
else:
cul[key] = 0
cul[key] += 1
return res 给你一个整数数组 nums 和一个整数 k ,编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组:
子数组大小 至少为 2 ,且 子数组元素总和为 k 的倍数。 如果存在,返回 true ;否则,返回 false 。
如果存在一个整数 n ,令整数 x 符合 x = n * k ,则称 x 是 k 的一个倍数。0 始终视为 k 的一个倍数。
示例 1:
输入:nums = [23,2,4,6,7], k = 6 输出:true 解释:[2,4] 是一个大小为 2 的子数组,并且和为 6 。
在上一题的基础上,需要对记录余数的索引,通过索引相减,以满足条件。
class Solution(object):
def checkSubarraySum(self, nums, k):
Sum, cul = 0, {}
cul[0] = -1 # 余数为0时,索引为-1,以免第一次遇见可整除时,满足条件
for i in range(len(nums)):
Sum += nums[i]
key = (Sum % k + k) % k
if key in cul: # 查找k的倍数,如果存在,加1,
if (i - cul[key]) > 1:
return True
else:
continue # 仅仅保存最小的索引,其他的跳过
else:
cul[key] = i
return False给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
仍然需要运用上面的前缀和,同时需要运用双指针,前后移动。时间复杂度O(n)。
class Solution(object):
def minSubArrayLen(self, target, nums):
if target > sum(nums):
return 0
# 返回长度,头指针,尾指针,列表长度
res, head, tail, Sum, n = len(nums), 0, 0, 0, len(nums)
while tail < n:
# 先递增尾指针,直到值大于target
while Sum < target and tail < n:
Sum += nums[tail]
tail += 1
# 再递增头指针,以找到最短长度
while Sum >= target and head >= 0:
res = min(res, tail - head)
Sum -= nums[head]
head += 1
return res二分法,O(nlog(n))。
class Solution(object):
def minSubArrayLen(self, target, nums):
"""
:type target: int
:type nums: List[int]
:rtype: int
"""
left, right, res = 0, len(nums), 0
def helper(size):
sum_size = 0
for i in range(len(nums)):
sum_size += nums[i]
if i >= size:
sum_size -= nums[i-size]
if sum_size >= target:
return True
return False
while left<=right:
mid = (left+right)//2 # 滑动窗口大小
if helper(mid): # 如果这个大小的窗口可以那么就缩小
res = mid
right = mid-1
else: # 否则就增大窗口
left = mid+1
return res返回 A 的最短的非空连续子数组的长度,该子数组的和至少为 K 。
如果没有和至少为 K 的非空子数组,返回 -1 。
示例 1:
输入:A = [1], K = 1 输出:1 示例 2:
输入:A = [1,2], K = 4 输出:-1 示例 3:
输入:A = [2,-1,2], K = 3 输出:3
由于存在负数,上一题方法不可用。
class Solution:
def shortestSubarray(self, nums: List[int], target: int) -> int:
n = len(nums)
sum = [0]*(n+1)
for i in range(n):
sum[i+1] = sum[i] + nums[i] # 前缀和
res, L = deque(), n+1
for i in range(n+1):
# #若栈顶sum[res[-1]]比sum[i]大,那它一定不如sum[i]优,因为i作为起点比res[-1]更短,子数组和更有可能>=K.
while res and sum[res[-1]] > sum[i]:
res.pop()
#此时i作为终点,由res中sum单调递增,左边的sum更有可能使子数组和>=k,但起点越右子数组越短,所以从左往右找符合条件的最右起点,由于后面符合条件的终点(如y-res[0])不可能比i-res[0]更短,所以符合条件的起点用完就pop,不符合条件的起点保留看看后面有没有机会。
while res and (sum[i] - sum[res[0]])>=target:
L = min(L, i-res.popleft())
res.append(i)
return -1 if L==(n+1) else L假设你是一位顺风车司机,车上最初有 capacity 个空座位可以用来载客。由于道路的限制,车只能向一个方向行驶(也就是说,不允许掉头或改变方向,你可以将其想象为一个向量)。
这儿有一份乘客行程计划表 trips[][],其中 trips[i] = [num_passengers, start_location, end_location] 包含了第 i 组乘客的行程信息:
必须接送的乘客数量; 乘客的上车地点; 以及乘客的下车地点。 这些给出的地点位置是从你的 初始 出发位置向前行驶到这些地点所需的距离(它们一定在你的行驶方向上)。
请你根据给出的行程计划表和车子的座位数,来判断你的车是否可以顺利完成接送所有乘客的任务(当且仅当你可以在所有给定的行程中接送所有乘客时,返回 true,否则请返回 false)。
示例 1:
输入:trips = [[2,1,5],[3,3,7]], capacity = 4 输出:false 示例 2:
输入:trips = [[2,1,5],[3,3,7]], capacity = 5 输出:true
模拟法 [2, 1, 5]表示位置1处上车2人, 位置5处下车2人;
由此可见, 我们只要按实际情况去模拟,计算每次有人上车时是否会超载即可.
将[2, 1, 5]转换为[1, 2], [5, -2]。其中负数表示有人下车。
按位置由近到远排序, 位置相同的时候遵循先下后上的原则,即负数排在整数前。
class Solution(object):
def carPooling(self, trips, capacity):
"""
:type trips: List[List[int]]
:type capacity: int
:rtype: bool
"""
move = []
for it in trips:
move.append((it[1], it[0]))
move.append((it[2], -it[0]))
move.sort()
target = 0
for it in move:
target += it[1]
if target > capacity:
return False
return True采用累加,相减的方式.
class Solution(object):
def carPooling(self, trips, capacity):
"""
:type trips: List[List[int]]
:type capacity: int
:rtype: bool
"""
cap = [0] * 1001
for num, start, end in trips:
cap[end] -= num
cap[start] += num
res = capacity
for i in cap:
res -= i
if res < 0 :
return False
return True某城市有N个出租车站点,为了方便计算,假设这些站点程圆形部署,相邻两个站点之间的行车时间固定为5,每个站点内的出租车数量足够多。每辆车均在圆形线路上运行,方向可以顺时针,也可以逆时针,选择最短的路线运行,如果起始点、终点相同,则为无效订单,不处理。
现在有N个乘客使用APP下发订单,包含使用出租车的时间,上车的站点、下车的站点,请算整个运作周期最多有多少辆出租车同时运营。下车时间点的车辆不计算在运行车辆中。
输入描述: 第一行输入N和,x代表站点的数量,K代表乘客的数目 2<=N<=100,0 <=K<=10000之后行,分别输入使用车辆的起始时间,上车的站点工D,下车的站点ID,0<=起始时间<=1000
'''
# 输入
50 3
0 0 15
10 10 11
15 20 40
# 输出2
'''
N, K = list(map(int, input().strip().split()))
m = []
while True:
try:
time, startID, endID = list(map(int, input().strip().split()))
m.append([time, startID, endID])
except EOFError:
break
res, K = 0, len(m)
# 对上车时间进行遍历, 对同属于一个时间段的车进行统计
for i in range(1000):
tmp=0
# 对每个上车样本遍历
for j in range(K):
start, end = m[j][1], m[j][2]
diff = abs(start - end)
num = min(diff, N-diff) # 坐车站数
if m[j][0] <=i and i < m[j][0]+num*5: # 根据start和坐车站数,得出坐车样本所持续的时间段
tmp += 1
res = max(res, tmp)
print(res)给你一个长度为 n 的整数数组 nums,其中 n > 1,返回输出数组 output ,其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。
示例:
输入: [1,2,3,4] 输出: [24,12,8,6]
遇到数组问题,感到无处下手时,大家一般的方法是枚举几个数组,把过程手动算一遍,然后看规律。
还有一种办法是把数组泛化:
假设nums = [a0, a1, a2, ..., a[i-1], a[i], a[i+1], ... an]
看一下泛化结果下一般值的组成规律:
Mi-1 = a0 * a1 * ... a[i-2] * ai * a[i+1] * a[i+2] * ... an
Mi = a0 * a1 * ... a[i-1] * a[i+1] * ... * an
Mi+1 = a0 * a1 * ... * a[i] * a[i+2] * a[i+3] * ... * an现在假设:
Ti = a0 * a1 * ... * ai-1
Ri = a[i+1] * a[i+2] * ... * an把上面的公式替换成:
Mi-1 = Ti-1 * Ri-1
Mi = Ti * Ri
Mi+1 = Ti+1 * Ri+1现在的问题就转化成怎么求两个数Ti 和Ri。观察到:
T0 = a0
T1 = a0 * a1 = T0 * a1
T2 = a0 * a1 * a2 = T1 * a2并且:
Rn-1 = a[n-1]
Rn-2 = a[n-1] * a[n-2] = Rn-1 * a[n-2]
Rn-3 = a[n-1] * a[n-2] * a[n-3] = Rn-2 * a[n-3]所以求Ti和Ri的过程拆分成了两个遍历过程,一次从左到右扫,一次从右到左扫。扫到 a[k]时, Tk = Tk-1 * a[k], Rk = Rk+1 * a[k]
class Solution(object):
def productExceptSelf(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
n, left, right, res = len(nums), 1, 1, [1]*len(nums)
for i in range(n):
# 左乘
res[i] *= left
left *=nums[i]
# 右乘
res[n-1-i] *= right
right *= nums[n-1-i]
return res给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
- 左右找出最高点
- 分别从两边往最高点遍历:如果下一个数比当前数小,说明可以接到水
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
n, left, right, res = len(height), [0]*len(height), [0]*len(height), 0
for i in range(1, n):
# 从左边往最高点遍历
left[i] = max(left[i-1], height[i-1])
# 从右边往最高点遍历
right[n-1-i] = max(right[n-i], height[n-i])
for i in range(n):
# 从左右中取最小值,才能装雨水
level = min(left[i], right[i])
res += max(0, level - height[i]) # 每个雨水的值
return res给你一个 m x n 的矩阵,其中的值均为非负整数,代表二维高度图每个单元的高度,请计算图中形状最多能接多少体积的雨水。
示例:
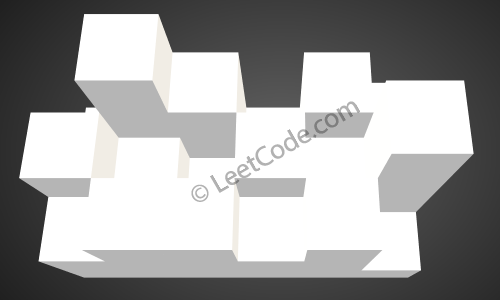
给出如下 3x6 的高度图: [ [1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1] ]
返回 4 。

如上图所示,这是下雨前的高度图
[[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]的状态。
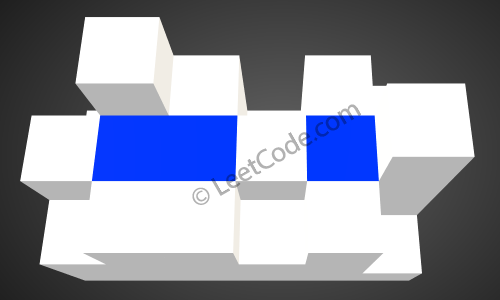
下雨后,雨水将会被存储在这些方块中。总的接雨水量是4。
这个视频很清晰 https://www.youtube.com/watch?v=cJayBq38VYw
from heapq import *
class Solution:
def trapRainWater(self, heightMap):
"""
水从高处往低处流,某个位置储水量取决于四周最低高度,从最外层向里层包抄,用小顶堆动态找到未访问位置最小的高度
"""
if not heightMap:return 0
imax = float('-inf')
ans = 0
heap = []
visited = set()
m = len(heightMap)
n = len(heightMap[0])
# 将最外层放入小顶堆
# 第一行和最后一行
for j in range(n):
# 将该位置的高度、横纵坐标插入堆
heappush(heap, [heightMap[0][j], 0, j])
heappush(heap, [heightMap[m - 1][j], m - 1, j])
visited.add((0, j))
visited.add((m - 1, j))
# 第一列和最后一列
for i in range(m):
heappush(heap, [heightMap[i][0], i, 0])
heappush(heap, [heightMap[i][n - 1], i, n - 1])
visited.add((i, 0))
visited.add((i, n - 1))
while heap:
h, i, j = heappop(heap)
# 之前最低高度的四周已经探索过了,所以要更新为次低高度开始探索
imax = max(imax, h)
# 从堆顶元素出发,探索四周储水位置
for x, y in [[0, 1], [1, 0], [0, -1], [-1, 0]]:
tmp_x = x + i
tmp_y = y + j
# 是否到达边界
if not (0<= tmp_x< m) or not (0<= tmp_y< n) or (tmp_x, tmp_y) in visited:
continue
visited.add((tmp_x, tmp_y))
if heightMap[tmp_x][tmp_y] < imax:
ans += imax - heightMap[tmp_x][tmp_y]
heappush(heap, [heightMap[tmp_x][tmp_y], tmp_x, tmp_y])
return ans给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
因而考虑排序+双指针:
- 特判,对于数组长度 n,如果数组为 null 或者数组长度小于 3,返回 [][]。
- 对数组进行排序。
- 遍历排序后数组:
- 若 nums[i]>0:因为已经排序好,所以后面不可能有三个数加和等于 0,直接返回结果。
- 对于重复元素:跳过,避免出现重复解
- 令左指针 L=i+1,右指针 R=n-1,当 L<R 时,执行循环:
- 当 nums[i]+nums[L]+nums[R]==0,执行循环,判断左界和右界是否和下一位置重复(指针位置不断变化,直到未出现重复元素),去除重复解。并同时将 L,R 移到下一位置,寻找新的解。
- 若和大于 0,说明 nums[R]太大,R左移
- 若和小于 0,说明 nums[L]太小,L右移
class Solution(object):
def threeSum(self, nums):
n = len(nums)
if n<3: return []
# 先排序,关键!
nums.sort()
result = []
for i in range(n):
if nums[i]>0:
return result
if i > 0 and nums[i-1]==nums[i]: # 重复元素跳过
continue
# 两指针
L = i + 1
R = n - 1
while (L < R):
if (nums[i] + nums[L] + nums[R])==0: # 满足条件
result.append([nums[i], nums[L], nums[R]])
while (L < R and nums[L] == nums[L + 1]): # 不断移动指针,直到不再重复
L +=1
while (L < R and nums[R] == nums[R - 1]): # 不断移动指针,直到不再重复
R -=1
# 移动指针
L +=1
R -=1
elif (nums[i] + nums[L] + nums[R])>0:
R -=1
else:
L +=1
return result
nums = [-2,0,3,-1,4,0,3,4,1,1,1,-3,-5,4,0]
s = Solution()
print(s.threeSum(nums)) 给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
动态规划:
因为是乘积的关系,nums[i] 数值的正负,与前面的状态值是有联系的,具体如下:
- 当 nums[i] > 0 时:
- 与最大值的乘积依然是最大值
- 与最小值的乘积依然是最小值
- 当 nums[i] < 0 时:
- 与最大值的乘积变为最小值
- 与最小值的乘积变为最大值
- 当 nums[i] = 0 时,这里无论最大最小值,最终结果都是 0,这里其实可以合并在上面任意一种情况。
class Solution(object):
def maxProduct(self, nums):
mi = ma = res = nums[0]
for i in range(1, len(nums)):
if nums[i] < 0: # 元素值小于0,最大、最小值互换,因为与正数相乘后,最小变最大,最大变最小
mi, ma = ma, mi
ma = max(ma * nums[i], nums[i]) # 最大值更新
mi = min(mi * nums[i], nums[i])
res = max(res, ma)
return res给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。
输入:nums = [3,30,34,5,9] 输出:"9534330"
自定义一种排序方式 比较 s1 + s2 和 s2 + s1
# 冒泡排序
class Solution(object):
def largestNumber(self, nums):
n = len(nums)
for i in range(n):
for j in range(i+1, n):
# 对比前后组成的数,以大小交换顺序
if int(str(nums[i])+str(nums[j])) < int(str(nums[j])+str(nums[i])):
nums[i], nums[j] = nums[j], nums[i]
res = ''.join(str(item) for item in nums)
return str(int(res))
# 希尔排序
class Solution(object):
def largestNumber(self, nums):
n = len(nums)
step = int(n/2)
while step > 0:
for i in range(step, n):
while i >= step and int(str(nums[i-step])+str(nums[i])) < int(str(nums[i])+str(nums[i-step])):
nums[i], nums[i-step] = nums[i-step], nums[i]
i -=step
step=int(step/2)
res = ''.join(str(item) for item in nums)
return str(int(res))
# 采用cmp_to_key 函数,可以接受两个参数,将两个参数做处理,比如做和做差,转换成一个参数,就可以应用于key关键字
class Solution(object):
def largestNumber(self, nums):
from functools import cmp_to_key
return str(int(''.join(sorted(map(str, nums), key=cmp_to_key(lambda x,y:int(y+x)-int(x+y))))))
# cmp_to_key的例子
from functools import cmp_to_key
L=[9,2,23,1,2]
sorted(L,key=cmp_to_key(lambda x,y:y-x))
输出:
[23, 9, 2, 2, 1]给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组,并输出它的长度。
示例 1:
输入:nums = [2,6,4,8,10,9,15] 输出:5 解释:你只需要对 [6, 4, 8, 10, 9] 进行升序排序,那么整个表都会变为升序排序。
从左到右循环,记录最大值为 max,若 nums[i] < max,则表明位置 i 需要调整, 循环结束,记录需要调整的最大位置 i 为 high;同理,从右到左循环,记录最小值为 min,若 nums[i] > min,则表明位置 i 需要调整,循环结束,记录需要调整的最小位置 i 为 low.
class Solution(object):
def findUnsortedSubarray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if not nums: return 0
max_, min_, high, low = nums[0], nums[-1], 0, len(nums)-1
for i in range(len(nums)):
max_ = max(nums[i], max_)
min_ = min(min_, nums[len(nums)-1-i])
if nums[i] < max_:
high = i
if nums[len(nums)-1-i] > min_:
low = len(nums)-1-i
return high - low +1 if high > low else 0给定一个包含 n + 1 个整数的数组 nums ,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,找出 这个重复的数 。
你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2] 输出:2
提示:
- 1 <= n <= 105
- nums.length == n + 1
- 1 <= nums[i] <= n
- nums 中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
先排序,然后看相邻元素是否有相同的,有直接return
class Solution(object):
def findDuplicate(self, nums):
n = len(nums)
nums.sort()
pre = nums[0]
for i in range(1,n):
if pre == nums[i]:
return pre
pre = nums[i]
# 集合法
class Solution(object):
def findDuplicate(self, nums):
s = set()
for num in nums:
if num in s:
return num
else:
s.add(num)给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1] 输出: 1
异或的规律:Y = A’ · B + A · B’
- 交换律:a ^ b ^ c=a ^ c ^ b
- 恒等律:任何数于0异或为任何数 0 ^ n=n
- (归零律)相同的数异或为0: n ^ n= 0
class Solution(object):
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
res = 0
for it in nums:
res ^= it
return res给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
示例 1:
输入:nums = [2,2,3,2] 输出:3 示例 2:
输入:nums = [0,1,0,1,0,1,99] 输出:99
在两个数相同的情况下,加上第三个
- x & ~x = 0
- x & ~0 = x
class Solution(object):
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
a = b = 0
for it in nums:
a = (a^it) & ~b
b = (b^it) & ~a
return a给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
进阶:你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现?
示例 1:
输入:nums = [1,2,1,3,2,5] 输出:[3,5] 解释:[5, 3] 也是有效的答案。 示例 2:
输入:nums = [-1,0] 输出:[-1,0]
采用字典数据进行计算,上面均可用此法:
class Solution(object):
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
m, res = {}, []
for it in nums:
if it not in m:
m[it] = 0
m[it] += 1
for it in m.keys():
if m[it] == 1:
res.append(it)
return res给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
进阶:
你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?
示例 1:
输入:nums = [3,0,1] 输出:2 解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
- 恒等律:任何数于0异或为任何数 0 ^ n=n
- (归零律)相同的数异或为0: n ^ n= 0
位运算:
class Solution(object):
def missingNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
n = res = len(nums)
for i in range(n):
res ^= nums[i]^i
return res求和:
class Solution(object):
def missingNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
n = len(nums)
return int(n*(n+1)/2) - sum(nums)给定两个字符串 s 和 t,它们只包含小写字母。
字符串 t 由字符串 s 随机重排,然后在随机位置添加一个字母。
请找出在 t 中被添加的字母。
示例 1:
输入:s = "abcd", t = "abcde" 输出:"e" 解释:'e' 是那个被添加的字母。
字典法统计个数:
class Solution(object):
def findTheDifference(self, s, t):
"""
:type s: str
:type t: str
:rtype: str
"""
if len(s)==0: return t
dic = {}
# 统计s中的元素个数
for it in s:
if it not in dic:
dic[it] = 0
dic[it] += 1
# 统计t中的个数
for it in t:
if it not in dic: return it
dic[it] -= 1
# 再判断个数小于0的
for it in dic.keys():
if dic[it] <0: return it
# 转变成ASCII码,相加,异或
class Solution(object):
def findTheDifference(self, s, t):
'''
1.每一个字符都对应一个 ASCII 数字,那么那个不同的数字的 ASCII 码就等于 t 的所有字符码之和 - s 的
2.ord 函数将单个字符转换为 ASCII 码, chr相反
'''
return chr(sum(map(ord, t)) - sum(map(ord, s)))
# 逐元素比较
class Solution(object):
def findTheDifference(self, s, t):
s = sorted(s)
t = sorted(t)
for i in range(len(s)):
if s[i] != t[i]:
return t[i]
return t[-1]集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数字重复 。
给定一个数组 nums 代表了集合 S 发生错误后的结果。
请你找出重复出现的整数,再找到丢失的整数,将它们以数组的形式返回。
示例 1:
输入:nums = [1,2,2,4] 输出:[2,3] 示例 2:
输入:nums = [1,1] 输出:[1,2]
class Solution(object):
def findErrorNums(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
nums.sort()
dic, res = {}, []
for it in nums:
if it not in dic: dic[it] = 0
dic[it] += 1
for it in dic.keys():
if dic[it] == 2: res.append(it)
for i in range(1, len(nums)+1):
if i not in dic.keys(): res.append(i)
return res
# 采用集合
class Solution(object):
def findErrorNums(self, nums):
n1 = sum(nums)-sum(set(nums))
n2 = sum(range(len(nums)+1))-sum(set(nums))
return [n1,n2]给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0] 输出:3 示例 2:
输入:nums = [3,4,-1,1] 输出:2 示例 3:
输入:nums = [7,8,9,11,12] 输出:1
- 先排序,时间复杂度超过了!!!
- 切掉非正数
- 再判断剩余的整数
- 如果最小数大于1,return 1
- 如果不是,两元素逐一对比,差值大于1,nums[i-1] + 1
- 否则返回,nums[-1]+1
class Solution(object):
def firstMissingPositive(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
nums.sort()
idx = -1
for i in range(len(nums)):
if nums[i]>0:
idx = i
break
if idx == -1:
return 1
else:
nums=nums[idx:]
if nums[0]>1:
return 1
else:
for i in range(1, len(nums)):
if nums[i] - nums[i-1] > 1:
return nums[i-1] + 1
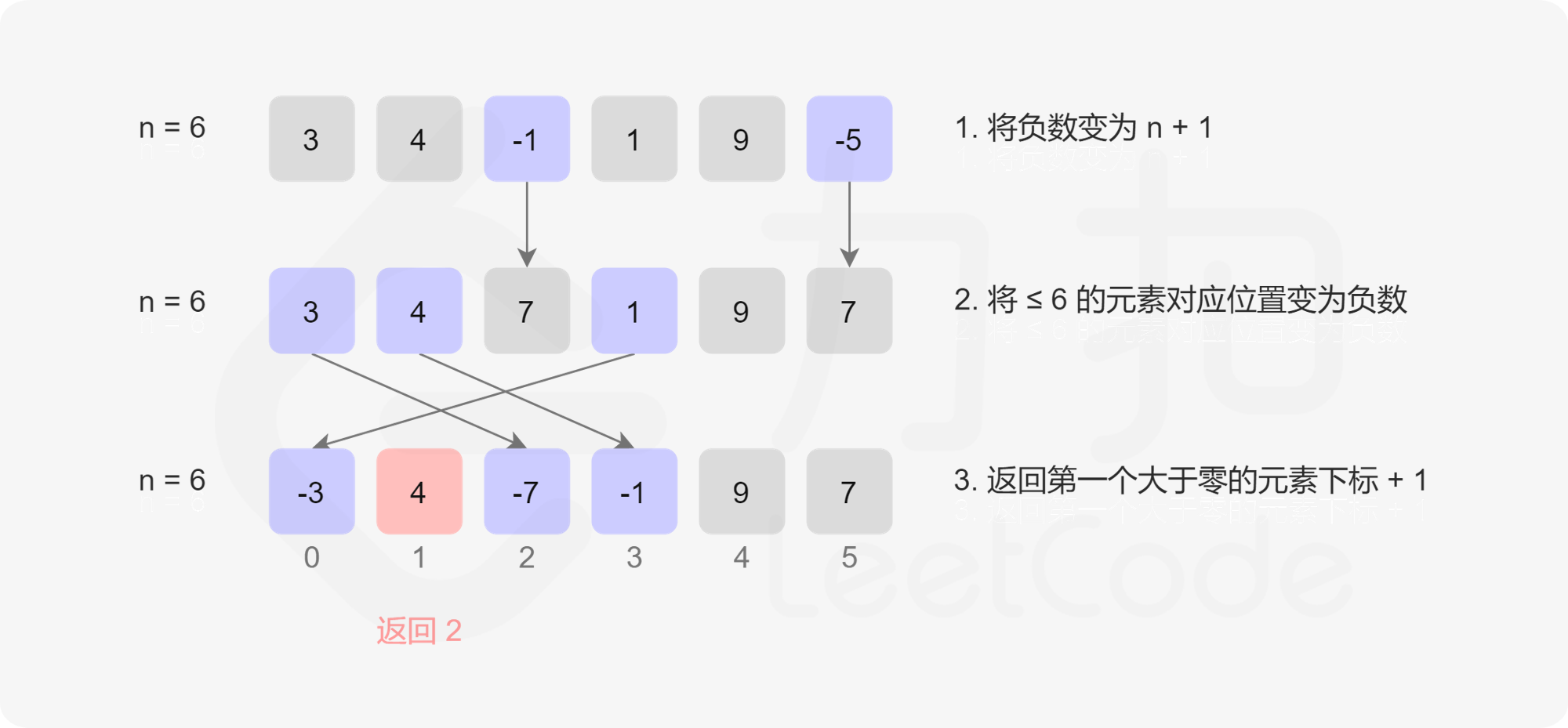
return nums[-1]+1实际上,对于一个长度为 NN 的数组,其中没有出现的最小正整数只能在 [1, N+1][1,N+1] 中。这是因为如果 [1, N][1,N] 都出现了,那么答案是 N+1,否则答案是 [1, N][1,N] 中没有出现的最小正整数。这样一来,我们将所有在 [1, N][1,N] 范围内的数放入哈希表,也可以得到最终的答案。而给定的数组恰好长度为 N,这让我们有了一种将数组设计成哈希表的思路:
我们对数组进行遍历,对于遍历到的数 x,如果它在 [1, N][1,N] 的范围内,那么就将数组中的第 x-1 个位置(注意:数组下标从 0 开始)打上「标记」。在遍历结束之后,如果所有的位置都被打上了标记,那么答案是 N+1,否则答案是最小的没有打上标记的位置加 1。
class Solution(object):
def firstMissingPositive(self, nums):
n = len(nums)
for i in range(n):
if nums[i] <= 0:
nums[i] = n + 1
for i in range(n):
num = abs(nums[i])
if num <= n:
nums[num - 1] = -abs(nums[num - 1])
for i in range(n):
if nums[i] > 0:
return i + 1
return n + 1写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
示例:
输入: a = 1, b = 1 输出: 2
A+B可以先转化为A^B和A&B两个值,由于A&B是进位值,因此需要整体向前移动一位才算进位,如此一来就得到加法的第一步转化公式:
A+B=A^B+(A&B)<<1;
01+01=00+10;(二进制表示)
class Solution(object):
def add(self, a, b):
"""
:type a: int
:type b: int
:rtype: int
"""
# (n & 0xffffffff)进行这种变换的原因是,如果存在负数则需要转换成补码的形式,正数补码是他本身
a &= 0xffffffff#
b &= 0xffffffff
while b != 0:
carry = ((a & b) << 1) & 0xffffffff#如果是负数,转换成补码形式
a ^= b
b = carry
if a < 0x80000000:#如果是正数的话直接返回
return a
else:
return ~(a^0xffffffff)#是负数的话,转化成其原码给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入:x = 123 输出:321 示例 2:
输入:x = -123 输出:-321 示例 3:
输入:x = 120 输出:21 示例 4:
输入:x = 0 输出:0
class Solution:
def reverse(self, x: int) -> int:
if x >= 0:
ans = int(str(x)[::-1])
else:
ans =- int(str(-x)[::-1])
if -2**31 <= ans <= 2**31-1:
return ans
else:
return 0给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:[3,2,3] 输出:3 示例 2:
输入:[2,2,1,1,1,2,2] 输出:2
class Solution:
def majorityElement(self, nums: List[int]) -> int:
if len(nums) < 2: return nums[0]
dic, n = {}, len(nums)
for i in nums:
if i not in dic:
dic[i] = 1
else:
dic[i] += 1
if dic[i] > n//2:
return iN 对情侣坐在连续排列的 2N 个座位上,想要牵到对方的手。 计算最少交换座位的次数,以便每对情侣可以并肩坐在一起。 一次交换可选择任意两人,让他们站起来交换座位。
人和座位用 0 到 2N-1 的整数表示,情侣们按顺序编号,第一对是 (0, 1),第二对是 (2, 3),以此类推,最后一对是 (2N-2, 2N-1)。
这些情侣的初始座位 row[i] 是由最初始坐在第 i 个座位上的人决定的。
示例 1:
输入: row = [0, 2, 1, 3] 输出: 1 解释: 我们只需要交换row[1]和row[2]的位置即可。 示例 2:
输入: row = [3, 2, 0, 1] 输出: 0 解释: 无需交换座位,所有的情侣都已经可以手牵手了。
class Solution(object):
def minSwapsCouples(self, row):
"""
每两个座位成一对,假定左边的人都是合法的不变,如果TA右边的人与TA匹配则
跳过,不匹配则找到TA的匹配对象的与TA右边的人交换。
"""
def find_another(n):
if n % 2 == 0:
return n + 1
else:
return n - 1
c = 0
for i in range(0, len(row), 2):
p1 = row[i]
p2 = find_another(p1)
if row[i+1] != p2:
j = row.index(p2)
row[i+1], row[j] = row[j], row[i+1]
c += 1
return c给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
双指针(滑框)
class Solution(object):
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
L = len(s)
if L<2: # 长度小于2,直接返回
return L
dp = 1 # 最长长度
head = 0 # 第一个指针
tail = 1 # 第二个指针
while tail < L:
if s[tail] not in s[head:tail]: # 如果末端元素不在已有的序列中,将指针指向下一个
tail +=1
else: # 如果已在序列中,获得已有的元素位置,并从此处重新开始计算
head += s[head:tail].index(s[tail])+1
dp = max(dp, tail-head) # 更新已有的最大值
return dp给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。 如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC" 示例 2:
输入:s = "a", t = "a" 输出:"a" 示例 3:
输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中, 因此没有符合条件的子字符串,返回空字符串。
滑动窗口适合求'连续'问题
left,right,如果窗口里面不符合条件,right+1, 如果符合,收缩左边的窗口,left+1
class Solution:
def minWindow(self, s: str, t: str) -> str:
# requires: T 的字典
# windows:窗口的字典
def is_valid(requires, windows):
for key, value in requires.items():
if windows.get(key,0) < value:
return False
return True
if not s or not t: return ''
N = len(s)
requires = {}
for item in t:
requires[item] = requires.get(item, 0) + 1
# 滑动窗口
windows = {s[0]:1}
left = right = 0
ret_len, ret = N, ''
while right < N:
if is_valid(requires, windows):
if right-left+1 <= ret_len:
ret_len = right-left+1
ret = s[left: right+1]
windows[s[left]] -= 1
left += 1
else:
right += 1
if right < N: # !!!!
windows[s[right]] = windows.get(s[right], 0) + 1
return ret给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
通过 "双端队列" ,也就是两边都能进能出的队列。
首先就是入队列,每次滑动窗口都把最大值左边小的数踢掉,也就是出队,后面再滑动窗口进行维护,这样相当于就是每一个数走过场。时间复杂度就是O(N*1)
遍历数组,当前元素为 num,索引为 i
- 当队列非空,左边界出界时(滑动窗口向右移导致的),更新左边界
- 当队列非空,将队列中索引对应的元素值比 num 小的移除
- 更新队列
- 当索引 i 大于 k-1,更新输出结果
class Solution(object):
def maxSlidingWindow(self, nums, k):
window, res = [], []
for i, num in enumerate(nums):
# 窗口滑动时的规律, 即滑动的位置超出了windows范围
if window and window[0] <= i-k:
window.pop(0)
# 把最大值左边的数小的清除,即判断新的数据Num,其与windows中值的比较:从最右端开始,Windows中的数据小于Num则弹出,否则停止,说明Windows中存的是从左到右,数值降低的序列。新的数据,需要与原有的序列进行判断
while window and nums[window[-1]] <= num:
window.pop()
window.append(i) # # 队首一定是滑动窗口的最大值的索引
if i >= k-1:
res.append(nums[window[0]])
return res
class Solution:
def maxSlidingWindow(self, nums, k):
deque = collections.deque()
ans = []
for i, num in enumerate(nums):
if deque and deque[0] <= i-k: # 窗口滑动时的规律, 即滑动的位置超出了windows范围
deque.popleft()
while deque and nums[deque[-1]] < num:
deque.pop()
deque.append(i)
if i >= k-1:
ans.append(nums[deque[0]])
return ans请根据每日 气温 列表 temperatures ,请计算在每一天需要等几天才会有更高的温度。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73] 输出: [1,1,4,2,1,1,0,0] 示例 2:
输入: temperatures = [30,40,50,60] 输出: [1,1,1,0] 示例 3:
输入: temperatures = [30,60,90] 输出: [1,1,0]
如上题一样维护递减栈,后入栈的元素总比栈顶元素小,递减序列的。
- 比对当前元素与栈顶元素的大小
- 若当前元素 < 栈顶元素:入栈
- 若当前元素 > 栈顶元素:弹出栈顶元素,记录两者下标差值即为所求天数
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
if not temperatures: return None
else: n = len(temperatures)
res, stack = [0]*n, []
for idx, t in enumerate(temperatures):
while stack and temperatures[stack[-1]] < t: # 当前值大于栈中最小值,右侧出栈
res[stack[-1]] = idx - stack[-1]
stack.pop()
stack.append(idx)
return res给你两个 没有重复元素 的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。
请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2]. 输出: [-1,3,-1] 解释: 对于 num1 中的数字 4 ,你无法在第二个数组中找到下一个更大的数字,因此输出 -1 。 对于 num1 中的数字 1 ,第二个数组中数字1右边的下一个较大数字是 3 。 对于 num1 中的数字 2 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
示例 2:
输入: nums1 = [2,4], nums2 = [1,2,3,4]. 输出: [3,-1] 解释: 对于 num1 中的数字 2 ,第二个数组中的下一个较大数字是 3 。 对于 num1 中的数字 4 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
class Solution:
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
stack, hash = [], {}
for n in nums2:
while stack and stack[-1] < n:
hash[stack.pop()] = n
stack.append(n)
return [hash.get(x, -1) for x in nums1]给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
输入: [1,2,1] 输出: [2,-1,2] 解释: 第一个 1 的下一个更大的数是 2; 数字 2 找不到下一个更大的数; 第二个 1 的下一个最大的数需要循环搜索,结果也是 2。 注意: 输入数组的长度不会超过 10000。
如温度题,将下标值改为元素值,循环的话,加上一倍即可。
class Solution:
def nextGreaterElements(self, nums: List[int]) -> List[int]:
if not nums: return None
else: n = len(nums)
res, stack = [-1]*n, []
tmp = nums+nums[:-1]
for idx, t in enumerate(tmp):
while stack and tmp[stack[-1]] < t:
res[stack[-1]] = t
stack.pop()
if idx < n: stack.append(idx) # 只保存一个数组的
return res给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1] 输出:true 解释:我们可以按以下顺序执行: push(1), push(2), push(3), push(4), pop() -> 4, push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1 示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2] 输出:false 解释:1 不能在 2 之前弹出。
提示:
1 <= pushed.length <= 1000 0 <= pushed[i] <= 1000 pushed 的所有元素 互不相同 popped.length == pushed.length popped 是 pushed 的一个排列
class Solution:
def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:
stack = []
i = 0
for it in pushed:
stack.append(it)
while stack and stack[-1] == popped[i]:
stack.pop()
i += 1
return len(stack)==0现有9发子弹,依次编号为1,2,3..9。子弹必须按照编号顺序依次压入弹夹,但是弹丈可以在不满的情况下就装入枪中射击,然后再次装了弹 例斑现有5发子弹需要装入弹夫,可以按照如下操作: (1)依次装入子弹:1、2、3、4、5,那么子弹时出的顺序为5、4、3、2、1 (2)先装两发子弹:1、2,然后射出1发了弹:2:再继续装入子弹:3、4、5,最终再全部射出。那么这五颗了3弹射出的顺序为2、5、4、3、1 输入描述: 待装入子弹的最大编号子弹射出的顺序 输出描述; 如果子弹射出的顺序是可能的,返回1,否则返回0
输入
6
213654
输出
1
6发子弹待装入弹夹 先装入子弹:1、2,然后射出两颗子弹:2、i再装入子弹:3,射出子弹:3 最后装入子弹:4、5、6,射出子弹:6、5、4最终子弹顺序为213654
同上
N = int(input().strip())
popped = list(map(int, list(str(input().strip()))))
pushed = list(range(1, N+1))
stack = []
i = 0
for it in pushed:
stack.append(it)
while stack and stack[-1] == popped[i]:
stack.pop()
i += 1
if len(stack)==0:
print(1)
else:
print(0)给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:A: [1,2,3,2,1],B: [3,2,1,4,7] 输出:3
解释:长度最长的公共子数组是 [3, 2, 1] 。
以类似卷积的方式进行:
class Solution:
def findLength(self, nums1, nums2):
self.res = 0
n1, n2 = len(nums1), len(nums2)
def getLength(i, j): # 找对齐部分最长
cur = 0
while i < n1 and j < n2:
if nums1[i] == nums2[j]: # 如果相等,则对齐长度增加,否则置0
cur += 1
self.res = max(self.res, cur)
else:
cur = 0
i, j = i + 1, j + 1
# 两个数组分别以自己的头怼另外一个数组一遍
for j in range(n2): getLength(0, j)
for i in range(n1): getLength(i, 0)
return self.res指针型:
class Solution(object):
def findLength(self, nums1, nums2):
res = dp = 0
if nums1 and nums2:
# chr为ASCII码转换,没懂
a, b, n = ''.join(map(chr, nums1)), ''.join(map(chr, nums2)), len(nums1)
while dp + res <n:
if a[dp:dp+res+1] in b:
res +=1
else:
dp +=1
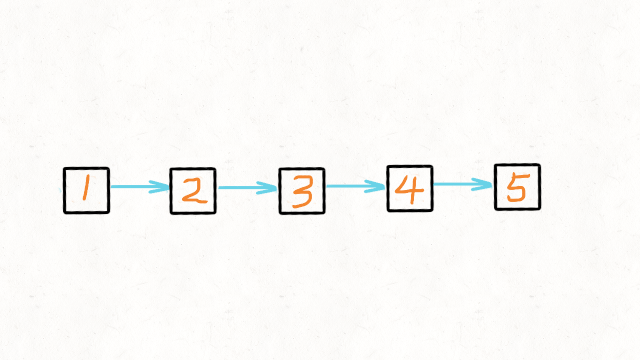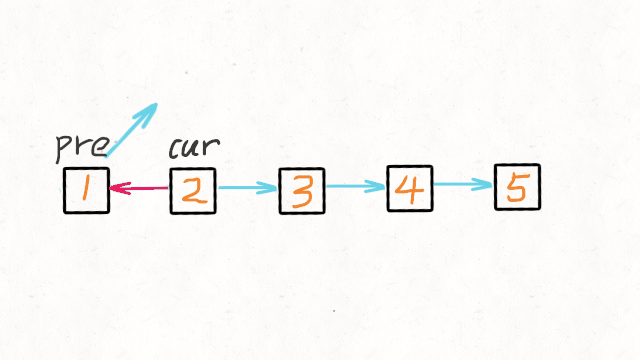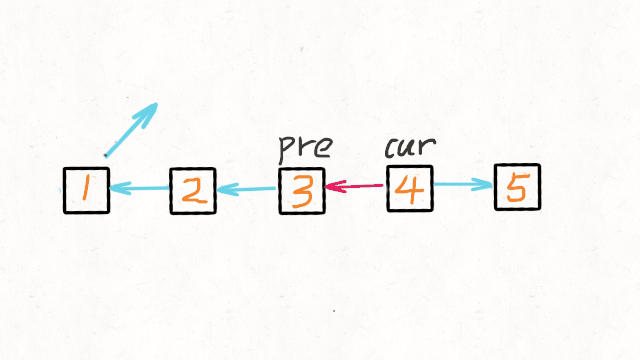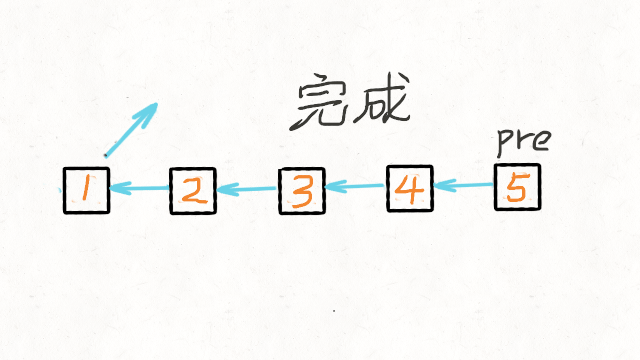
return res双指针迭代 我们可以申请两个指针:
- 第一个指针叫 pre,最初是指向 null 的。
- 第二个指针 cur 指向 head,然后不断遍历 cur。
- 每次迭代到 cur,都将 cur 的 next 指向 pre,然后 pre 和 cur 前进一位。
- 都迭代完了(cur 变成 null 了),pre 就是最后一个节点了。
动画演示如下:
class Solution(object):
def reverseList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
pre = None # 空值
current = head # 当前所在值
while current: # 当当前所在值不为空,也即未运行至链表末尾
temp = current.next # 将next值保存为中间变量
current.next = pre # 将next指向前一个
pre = current # 移动前一个为当下的值
current = temp # 当前值指向之前保存的next值,其实类似于对角线
# 以上可简化为一行,利用赋值即可
# current.next, pre, current = pre, current, current.next
return pre给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例 1:

输入:head = [1,2,3,4,5], left = 2, right = 4
头插法:
根据上面的图示,这里说下其中涉及的参数,以及其中反转过程中的步骤:
其中涉及的参数:
- dummy_node:哑节点,减少判断;
- pre:指向left 的前一个节点,反转过程中不变;
- cur:初始指向需要反转区域的第一个节点,也就是left的位置;
- next:指向cur 的下一个节点,跟随cur 变化。
其中反转过程中的步骤:
- 将cur 的下一个节点指向next 的下一个节点;
- 将 next 的下一个节点指向pre 的下一个节点;
- 将 pre 的下一个节点指向next。
循环上面三个步骤,直至反转结束。
class Solution(object):
def reverseBetween(self, head, left, right):
"""
:type head: ListNode
:type left: int
:type right: int
:rtype: ListNode
"""
dummy = ListNode()
dummy.next, pre = head, dummy
# 令 pre 指向 left 位置的前一个节点
for _ in range(left-1):
pre = pre.next
cur = pre.next
# 通过头插法,实现反转
for _ in range(left, right):
nxt = cur.next
cur.next = nxt.next
nxt.next = pre.next
pre.next = nxt
return dummy.next输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
给定一个链表: 1->2->3->4->5, 和 k = 2. 返回链表 4->5.
快慢指针,快的先走k步,然后再一起同步走。
class Solution(object):
def getKthFromEnd(self, head, k):
fast, slow = head, head
for _ in range(k): # 快指针先走k步
if fast:
fast = fast.next
else:
return None
while fast:
slow, fast = slow.next, fast.next
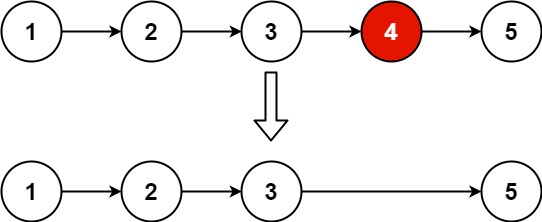
return slow给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
进阶:你能尝试使用一趟扫描实现吗?
示例 1:

输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
与上一题一样,快慢指针。
class Solution(object):
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
dummy = ListNode(0)
dummy.next, fast, slow = head, head, dummy
for _ in range(n):
if fast:
fast = fast.next
else:
return None
while fast:
slow, fast = slow.next, fast.next
slow.next = slow.next.next
return dummy.next或者
class Solution(object):
def removeNthFromEnd(self, head, n):
fast, slow = head, head
for _ in range(n):
if fast.next:
fast = fast.next
else:
return head.next # 由于提前了一位, 正常为None
while fast.next:
slow, fast = slow.next, fast.next
slow.next = slow.next.next
return head
# 以下报错
class Solution(object):
def removeNthFromEnd(self, head, n):
fast, slow = head, head
for _ in range(n):
if fast:
fast = fast.next
else:
return None
while fast: # 此时到达倒数第n个
slow, fast = slow.next, fast.next
# 此条件,第n个未删除,删除的是第n+1个,故如上采用fast.next,提前一个
slow.next = slow.next.next
return head存在一个按升序排列的链表,给你这个链表的头节点
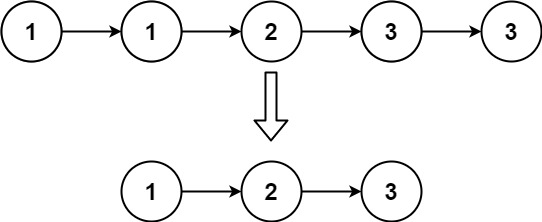
head,请你删除所有重复的元素,使每个元素 只出现一次 。返回同样按升序排列的结果链表。
示例 2:

输入:head = [1,1,2,3,3] 输出:[1,2,3]
class Solution:
def deleteDuplicates(self, head: ListNode) -> ListNode:
if not head: return None
dummy = ListNode(0)
dummy.next = head
while head and head.next:
if head.val == head.next.val: # 删除第二个重复的元素
head.next = head.next.next
else:
head = head.next
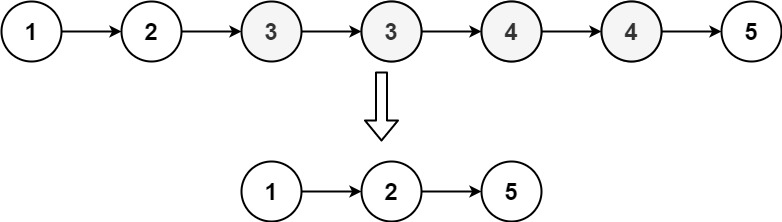
return dummy.next存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除链表中所有存在数字重复情况的节点,只保留原始链表中 没有重复出现 的数字。
返回同样按升序排列的结果链表。
示例 1:

输入:head = [1,2,3,3,4,4,5] 输出:[1,2,5]
class Solution:
def deleteDuplicates(self, head: ListNode) -> ListNode:
if not head: return None
tmp = ListNode(0, head)
dummy = tmp
# 需要采用tmp, 第一个元素可能就重复
while tmp.next and tmp.next.next:
if tmp.next.val == tmp.next.next.val:
x = tmp.next.val
while tmp.next and tmp.next.val==x: # 可能存在多个重复的
tmp.next = tmp.next.next
else:
tmp = tmp.next
return dummy.next给定一个单链表 L:L0→L1→…→Ln-1→Ln , 将其重新排列后变为: L0→Ln→L1→Ln-1→L2→Ln-2→…
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
给定链表 1->2->3->4->5, 重新排列为 1->5->2->4->3.
思路:重排列表,可以视为正反序列表,岔开插入,而插入长度为列表长度的一半。
class ListNode(object):
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution(object):
def reorderList(self, head):
if not head or not head.next: # 列表为空,或者只有一个元素
return None
# 快慢指针,用于确定链表的中间
slow = head
fast = head # 行进速度为2step
while fast.next and fast.next.next: # 确保前进有值
fast = fast.next.next
slow = slow.next
second = slow.next # 后半段链表head
node = slow.next.next # 下一个值
slow.next = None
second.next = None
while node: # 反转后半段链表
tmp = node.next
node.next = second
second = node
node = tmp
first = head # 前半段链表
while second:
tmp = first.next # 保存前半段链表的下一个值
first.next = second # 插入后半段链表的值
tmp2 = second.next # 保存后半段链表的下一个值
second.next = tmp # 传递前半段链表的下一个值
first = tmp # 移动至前半段链表的下一个值
second = tmp2 # 移动至后半段链表的下一个值
return first
L = ListNode(1)
L.next = ListNode(2)
L.next.next = ListNode(3)
L.next.next.next = ListNode(4)
L.next.next.next.next = ListNode(5)
s = Solution()
print(s.reorderList(L))
# 简化版
class Solution(object):
def reorderList(self, head):
if not head or not head.next:
return None
slow = fast = first = head
while fast.next and fast.next.next:
fast, slow = fast.next.next, slow.next
second, node, slow.next, second.next = slow.next, slow.next.next, None, None
while node:
node.next, second, node = second, node, node.next
while second:
first.next, second.next, first, second = second, first.next, first.next, second.next
return first将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
class Solution(object):
def mergeTwoLists(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
if not (l1 and l2): # 判断l1或l2中,存在一个为None
return l1 if l1 else l2
if l1.val < l2.val: # 如果l1的当前值小于l2,后面的值接在l1后面,并递归追溯
l1.next = self.mergeTwoLists(l1.next, l2)
return l1
else: # 相反情况
l2.next = self.mergeTwoLists(l1, l2.next)
return l2给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组如下: [ 1->4->5, 1->3->4, 2->6 ] 将它们合并到一个有序链表中得到。 1->1->2->3->4->4->5->6
思路:合并k个,则可以分解为若干个子问题,链表两两合并,如上一题。即为分治**。
class Solution(object):
def mergeKLists(self, lists):
"""
:type lists: List[ListNode]
:rtype: ListNode
"""
n = len(lists)
if n==0: return None
if n==1: return lists[0]
mid = n//2 # 分治,成为两部分链表
return self.mergeTwo(self.mergeKLists(lists[:mid]), self.mergeKLists(lists[mid:]))
def mergeTwo(self, l1, l2):
if not (l1 and l2):
return l1 if l1 else l2
if l1.val < l2.val:
l1.next = self.mergeTwo(l1.next, l2)
return l1
else:
l2.next = self.mergeTwo(l1, l2.next)
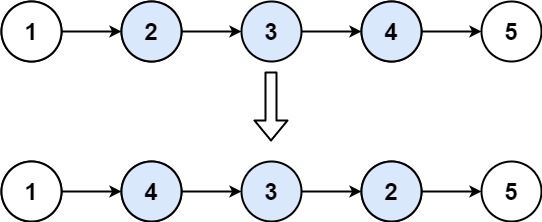
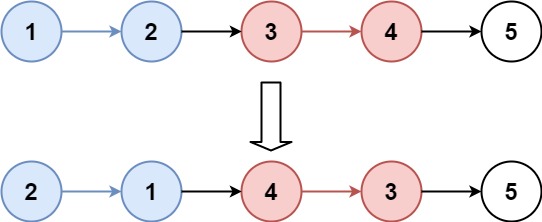
return l225-K 个一组翻转链表(有点难)
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
进阶:
你可以设计一个只使用常数额外空间的算法来解决此问题吗? 你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
输入:head = [1,2,3,4,5], k = 2 输出:[2,1,4,3,5]
尾插法。
直接举个例子:k = 3。
pre
tail head
dummy 1 2 3 4 5
# 我们用tail 移到要翻转的部分最后一个元素
pre head tail
dummy 1 2 3 4 5
cur
# 我们尾插法的意思就是,依次把cur移到tail后面
pre tail head
dummy 2 3 1 4 5
cur
# 依次类推
pre tail head
dummy 3 2 1 4 5
cur
....class Solution(object):
def reverseKGroup(self, head, k):
"""
:type head: ListNode
:type k: int
:rtype: ListNode
"""
dummy = ListNode()
dummy.next, pre, tail = head, dummy, dummy # 进行复制变量名
while True:
count = k
while count and tail: # 移动k个
count -= 1
tail = tail.next
if not tail: break # 如果是末尾,直接跳出
head = pre.next # 重新复制变量名 [0,1,2,3,4,5]
while pre.next != tail:
cur = pre.next # 获取下一个元素 cur=[1,2,3,4,5], cur.val=1 | pre:[0,2,3,4,5], cur:[2,3,4,5],cur.val=2
# pre与cur.next连接起来,此时cur(孤单)掉了出来
pre.next = cur.next # pre:[0,2,3,4,5] | pre:[0,3,4,5]
cur.next = tail.next # 和剩余的链表连接起来, tail:[3,4,5], cur:[1,4,5] | tail:[3,1,4,5], cur:[2,1,4,5]
tail.next = cur #插在tail后面, tai:[3,1,4,5] | tai:[3,2,1,4,5]
# 改变 pre tail 的值
pre = head #[1,4,5]
tail = head
return dummy.next递归整体想法
- 如果长度l小于k那直接返回;否则, 记链表由长度为k和$l_1 $的两个链表组成,$l=k+l_1$
- 翻转结果=【直接翻转前段长度为k的链表】 + 【k个一组翻转第二段长度为$l_1 $的链表】
- 前者迭代翻转(记得保留翻转前的头节点) 后者递归调用函数
class Solution(object):
def reverseKGroup(self, head, k):
# 如果长度>k, 找第k+1个节点; 如果长度小于k, 中途返回head
h, i = head, 1
for i in range(k):
if not h: return head
h = h.next # 走k个节点
# 翻转前k个节点组成的链表 保留头节点 以便连接后面的翻转链表
tail_reverse = head
pre, cur = None, head
# 反转链表子程序
while cur!=h:
temp=cur.next
cur.next=pre
pre, cur=cur, temp
# 换成一行: cur.next, pre, cur = pre, cur, cur.next
head_reverse=pre
# 连接两端
tail_reverse.next = self.reverseKGroup(h, k)
return head_reverse或者:
class Solution:
def reverseKGroup(self, head, k):
cur = head
count = 0
while cur and count!= k:
cur = cur.next
count += 1
if count == k:
cur = self.reverseKGroup(cur, k)
while count:
head.next, cur, head= cur, head, head.next
count -= 1
head = cur
return head给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
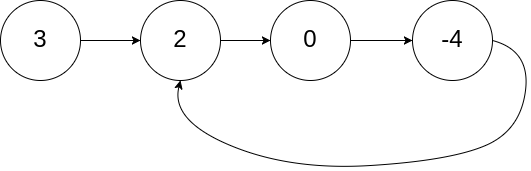
本题核心思路:走 a+nb 步一定处于环的入口位置
假设链表环前有 a个节点,环内有 b个节点
- 利用快慢指针 fast 和 slow,fast 一次走两步,slow 一次走一步
- 当两个指针第一次相遇时,假设 slow 走了 s步,下面计算 fast 走过的步数
- fast 比 slow多走了 n个环:f = s + nb
- fast 比 slow多走一倍的步数:f = 2s--> 跟上式联立可得 s = nb
- 综上计算得,f = 2nb,s = nb
class Solution(object):
def hasCycle(self, head):
slow = fast = head
while True:
if not fast or not fast.next:
return False
slow = slow.next
fast = fast.next.next
if slow == fast:
break
return True给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
说明:不允许修改给定的链表。
进阶:你是否可以使用 O(1) 空间解决此题?
示例 1:

输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
本题核心思路:走 a+nb 步一定处于环的入口位置
假设链表环前有 a个节点,环内有 b个节点
- 利用快慢指针 fast 和 slow,fast 一次走两步,slow 一次走一步
- 当两个指针第一次相遇时,假设 slow 走了 s步,下面计算 fast 走过的步数
- fast 比 slow多走了 n个环:f = s + nb
- fast 比 slow多走一倍的步数:f = 2s--> 跟上式联立可得 s = nb
- 综上计算得,f = 2nb,s = nb
- 也就是两个指针第一次相遇时,都走过了环的倍数,那么再走 a步就可以到达环的入口
- 让 fast从头再走,slow留在原地,fast和 slow均一次走一步,当两个指针第二次相遇时,fast走了 a步,slow走了 a+nb步
此时 slow就在环的入口处,返回 slow
class Solution(object):
def detectCycle(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
slow = fast = head
while True: # 先判断是否有环
if not fast or not fast.next:
return None
slow = slow.next
fast = fast.next.next
if slow == fast:
break
fast = head
while slow != fast: # 找到入口
fast = fast.next
slow = slow.next
return slow给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
示例 1:

输入:head = [1,2,2,1] 输出:true 示例 2:

输入:head = [1,2] 输出:false
先用快慢指针找到中点位置,在逐个左右两侧值比较。中点两侧比较,存在两种情况:
- 列表长度为奇数个,中间所在值为分界点,两侧值逐一比较
- 列表长度为偶数个,如示例1,两侧比较
class Solution:
def isPalindrome(self, head):
if not head or not head.next: return True
slow = fast = head
stack = []
# 找到中间点
while fast and fast.next:
stack.append(slow.val) # 保存左半部分值
slow = slow.next
fast = fast.next.next
while slow:
if slow.val == stack[-1]: # 长度为偶数,或奇数的两侧对称情况
slow = slow.next
stack.pop()
elif slow.next and slow.next.val == stack[-1]: # 奇数长度,下一个值才对称
slow = slow.next
else: # 无对称
break
return False if stack else True给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。例如,121 是回文,而 123 不是。
示例 1:
输入:x = 121 输出:true 示例 2:
输入:x = -121 输出:false 解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
如上,转化为字符串,按照奇偶长度分别处理:
class Solution:
def isPalindrome(self, x):
x_list = list(str(x))
n = len(x_list)
if n==1: return True
mid = n//2
stack = x_list[:mid]
res = x_list[mid:]
if n%2==1: res.pop(0)
for it in res:
if it == stack[-1]:
stack.pop()
else: break
return False if stack else True给定一个包含 n + 1 个整数的数组 nums ,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,找出 这个重复的数 。
你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2] 输出:2
提示:
- 1 <= n <= 105
- nums.length == n + 1
- 1 <= nums[i] <= n
- nums 中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
数组有重复元素时候, 通过索引号移动会有环出现
比如: nums = [ 1, 3, 4, 2, 3]
class Solution:
def findDuplicate(self, nums):
slow = nums[0]
fast = nums[nums[0]]
while slow != fast:
slow = nums[slow]
fast = nums[nums[fast]]
slow = 0
while slow != fast:
slow = nums[slow]
fast = nums[fast]
return slow给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
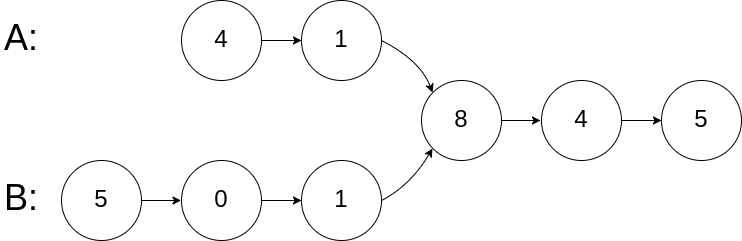
图示两个链表在节点 c1 开始相交:
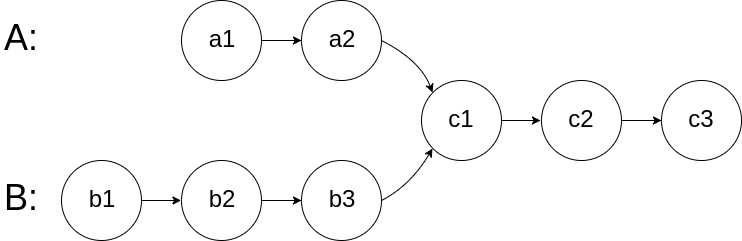
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
示例 1:

输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3 输出:Intersected at '8' 解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。 在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
if not headA or not headB: return None
pA, pB = headA, headB
while pA != pB:
pA = pA.next if pA else headB
pB = pB.next if pB else headA
return pA给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
进阶:
你可以在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
示例 1:

输入:head = [4,2,1,3] 输出:[1,2,3,4]
class Solution(object):
def sortList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if not head or not head.next: return head
slow, fast = head, head.next
while fast and fast.next:
slow = slow.next
fast = fast.next.next
mid = slow.next
slow.next = None # 断开链表
left, right = self.sortList(head), self.sortList(mid)
return self.merge(left, right)
def merge(self, left, right):
if not (left and right): return left if left else right
if left.val < right.val:
left.next = self.merge(left.next, right)
return left
else:
right.next = self.merge(left, right.next)
return right对链表进行插入排序。
插入排序的动画演示如上。从第一个元素开始,该链表可以被认为已经部分排序(用黑色表示)。 每次迭代时,从输入数据中移除一个元素(用红色表示),并原地将其插入到已排好序的链表中。
插入排序算法:
- 插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
- 每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
- 重复直到所有输入数据插入完为止。
示例 1:
输入: 4->2->1->3 输出: 1->2->3->4
class Solution(object):
def insertionSortList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
dummy = ListNode(0, head)
# 初始化两个节点,tail代表的是前面排过序的链表的尾节点,
# current代表的是尾节点之后的那个节点,也就是未排序部分的第一个节点
tail, cur = head, head.next
while cur:
# 比较尾节点与current节点的值,如果current节点的值更大,
# 那么不需要进行额外的插入操作,只需要更新尾节点到current节点所在的位置
if tail.val <= cur.val:
tail = tail.next
# 如果current节点比排序后的那部分的链表的尾节点小,那就要从头部遍历已经排序过的链表部分
else:
tmp = dummy
# 注意下面比较值大小时,我们实际上是从temp.next(也就是头节点)开始比较的
# 当下面的while循环停止时,我们久找到了第一个比current的值大的节点,
# 也就是temp.next这个节点所在的位置
while tmp.next.val <= cur.val:
tmp = tmp.next
# 上面的while循环找到了current应该插入的位置,开始插入操作
# 首先让tail指向current的下一个节点,这样current就可以放心的插入到前面排序过的链表的对应位置
tail.next = cur.next
# 让current.next指向第一个比它的值大的节点,也就是temp.next这个节点
current.next = temp.next
# 让后让temp节点(也就是temp.next这个节点的前一个节点)指向current这个节点
temp.next = current
# current这个指针从head.next位置,遍历了整个链表
current = tail.next
return dummy.next给你两个单词
word1和word2,请你计算出将word1转换成word2所使用的最少操作数 。
最直观的方法是暴力检查所有可能的编辑方法,取最短的一个。所有可能的编辑方法达到指数级,但我们不需要进行这么多计算,因为我们只需要找到距离最短的序列而不是所有可能的序列。
思路和算法
我们可以对任意一个单词进行三种操作:
-
插入一个字符;
-
删除一个字符;
-
替换一个字符。
题目给定了两个单词,设为 A 和 B,这样我们就能够六种操作方法。
但我们可以发现,如果我们有单词 A 和单词 B:
-
对单词 A 删除一个字符和对单词 B 插入一个字符是等价的。例如当单词 A 为 doge,单词 B 为 dog 时,我们既可以删除单词 A 的最后一个字符e,得到相同的 dog,也可以在单词 B 末尾添加一个字符 e,得到相同的 doge;
-
同理,对单词 B 删除一个字符和对单词 A 插入一个字符也是等价的;
-
对单词 A 替换一个字符和对单词 B 替换一个字符是等价的。例如当单词 A 为 bat,单词 B 为 cat 时,我们修改单词 A 的第一个字母 b -> c,和修改单词 B 的第一个字母 c -> b 是等价的。
这样以来,本质不同的操作实际上只有三种:
-
在单词 A 中插入一个字符;
-
在单词 B 中插入一个字符;
-
修改单词 A 的一个字符。
这样以来,我们就可以把原问题转化为规模较小的子问题。我们用 A = horse,B = ros 作为例子,来看一看是如何把这个问题转化为规模较小的若干子问题的。
-
在单词 A 中插入一个字符:如果我们知道 horse 到 ro 的编辑距离为 a,那么显然 horse 到 ros 的编辑距离不会超过 a + 1。这是因为我们可以在 a 次操作后将 horse 和 ro 变为相同的字符串,只需要额外的 1 次操作,在单词 A 的末尾添加字符 s,就能在 a + 1 次操作后将 horse 和 ro 变为相同的字符串;
-
在单词 B 中插入一个字符:如果我们知道 hors 到 ros 的编辑距离为 b,那么显然 horse 到 ros 的编辑距离不会超过 b + 1,原因同上;
-
修改单词 A 的一个字符:如果我们知道 hors 到 ro 的编辑距离为 c,那么显然 horse 到 ros 的编辑距离不会超过 c + 1,原因同上。
那么从 horse 变成 ros 的编辑距离应该为 min(a + 1, b + 1, c + 1)。
**注意:**为什么我们总是在单词 A 和 B 的末尾插入或者修改字符,能不能在其它的地方进行操作呢?答案是可以的,但是我们知道,操作的顺序是不影响最终的结果的。例如对于单词 cat,我们希望在 c 和 a 之间添加字符 d 并且将字符 t 修改为字符 b,那么这两个操作无论为什么顺序,都会得到最终的结果 cdab。
你可能觉得 horse 到 ro 这个问题也很难解决。但是没关系,我们可以继续用上面的方法拆分这个问题,对于这个问题拆分出来的所有子问题,我们也可以继续拆分,直到:
-
字符串 A 为空,如从 转换到 ro,显然编辑距离为字符串 B 的长度,这里是 2;
-
字符串 B 为空,如从 horse 转换到 ,显然编辑距离为字符串 A 的长度,这里是 5。
因此,我们就可以使用动态规划来解决这个问题了。我们用 D[i][j] 表示 A 的前 i 个字母和 B 的前 j 个字母之间的编辑距离。
如上所述,当我们获得 D[i][j-1],D[i-1][j] 和 D[i-1][j-1] 的值之后就可以计算出 D[i][j]。
-
D[i][j-1] 为 A 的前 i 个字符和 B 的前 j - 1 个字符编辑距离的子问题。即对于 B 的第 j 个字符,我们在 A 的末尾添加了一个相同的字符,那么 D[i][j] 最小可以为 D[i][j-1] + 1;
-
D[i-1][j] 为 A 的前 i - 1 个字符和 B 的前 j 个字符编辑距离的子问题。即对于 A 的第 i 个字符,我们在 B 的末尾添加了一个相同的字符,那么 D[i][j] 最小可以为 D[i-1][j] + 1;
-
D[i-1][j-1] 为 A 前 i - 1 个字符和 B 的前 j - 1 个字符编辑距离的子问题。即对于 B 的第 j 个字符,我们修改 A 的第 i 个字符使它们相同,那么 D[i][j] 最小可以为 D[i-1][j-1] + 1。特别地,如果 A 的第 i 个字符和 B 的第 j 个字符原本就相同,那么我们实际上不需要进行修改操作。在这种情况下,D[i][j] 最小可以为 D[i-1][j-1]。
那么我们可以写出如下的状态转移方程:
若 A 和 B 的最后一个字母相同: $$ \begin{aligned}
D[i][j] &= \min(D[i][j - 1] + 1, D[i - 1][j]+1, D[i - 1][j - 1])\ &= 1 + \min(D[i][j - 1], D[i - 1][j], D[i - 1][j - 1] - 1)
\end{aligned} $$
若 A 和 B 的最后一个字母不同:
所以每一步结果都将基于上一步的计算结果,示意如下:
对于边界情况,一个空串和一个非空串的编辑距离为 D[i][0] = i 和 D[0][j] = j,D[i][0] 相当于对 word1 执行 i 次删除操作,D[0][j] 相当于对 word1执行 j 次插入操作。
总结:
dp[i][j] 代表 word1 到 i 位置转换成 word2 到 j 位置需要最少步数
所以,
-
当 word1[i] == word2[j],dp[i][j] = dp[i-1][j-1];
-
当 word1[i] != word2[j],dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
其中,dp[i-1][j-1] 表示替换操作,dp[i-1][j] 表示删除操作,dp[i][j-1] 表示插入操作。
class Solution(object):
def minDistance(self, word1, word2):
"""
:type word1: str
:type word2: str
:rtype: int
"""
n1, n2 = len(word1), len(word2)
# 有一个字符串为空串
if n1 * n2 == 0:
return n1 + n2
# DP 数组
dp = [[0] * (n2 + 1) for _ in xrange(n1 + 1)]
# 边界状态初始化
for i in xrange(1, n1 + 1):
dp[i][0] = i
for j in xrange(1, n2 + 1):
dp[0][j] = j
# 计算所有 DP 值
for i in xrange(1, n1 + 1):
for j in xrange(1, n2 + 1):
if word1[i - 1] == word2[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
else:
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1
return dp[n1][n2]
# 内存优化
class Solution(object):
def minDistance(self, word1, word2):
"""
:type word1: str
:type word2: str
:rtype: int
"""
n1, n2 = len(word1), len(word2)
dp = [0] * (n2 + 1) #保留一行
dp[0] = 0
for j in xrange(1, n2 + 1):
dp[j] = j
for i in xrange(1, n1 + 1):
old_dp_j = dp[0]
dp[0] = i
for j in xrange(1, n2 + 1):
old_dp_j_1, old_dp_j = old_dp_j, dp[j]
if word1[i - 1] == word2[j - 1]:
dp[j] = old_dp_j_1
else:
dp[j] = min(dp[j], dp[j - 1], old_dp_j_1) + 1
return dp[n2]给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
此题跟上一题类似:
状态定义:
- dp[i][j] 表示text1[0~i-1]和text2[0~j-1]的最长公共子序列长度
- dp[0][0]等于0,等于dp数组总体往后挪了一个,免去了判断出界
转移方程:
- text1[i-1] == text2[j-1] 当前位置匹配上了: dp[i][j] = dp[i-1][j-1]+1
- text1[i-1] != text2[j-1] 当前位置没匹配上了 :dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
- base case: 任何一个字符串为0时都是零,初始化时候就完成了base case是赋值
class Solution(object):
def longestCommonSubsequence(self, text1, text2):
n1, n2 = len(text1), len(text2)
dp = [[0] * (n2 + 1) for _ in range(n1 + 1)]
for i in range(1, n1+1):
for j in range(1, n2+1):
if text1[i-1] == text2[j-1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[n1][n2]给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:A: [1,2,3,2,1],B: [3,2,1,4,7] 输出:3
解释:长度最长的公共子数组是 [3, 2, 1] 。
此题跟上一题类似,但不同的是,需要连续的数组,要考虑连续性。
状态定义:
- dp[i][j] 表示text1[0~i-1]和text2[0~j-1]的最长公共子序列长度
- dp[0][0]等于0,等于dp数组总体往后挪了一个,免去了判断出界
转移方程:
- text1[i-1] == text2[j-1] 当前位置匹配上了: dp[i][j] = dp[i-1][j-1]+1
- text1[i-1] != text2[j-1] 当前位置没匹配上了 :dp[i][j] = 0(这部分与上面不同,因为一旦不同,需要重新置0)
- base case: 任何一个字符串为0时都是零,初始化时候就完成了base case是赋值
class Solution(object):
def findLength(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: int
"""
n1, n2 = len(nums1), len(nums2)
dp = [[0]*(n2+1) for _ in range(n1+1)]
for i in range(1, n1+1):
for j in range(1, n2+1):
if nums1[i-1]==nums2[j-1]:
dp[i][j] = dp[i-1][j-1]+1
return max(max(item) for item in dp)
# 例如dp输出
3 2 1 4 7
1 0 0 1 0 0
2 0 1 0 0 0
3 1 0 0 0 0
2 0 2 0 0 0
1 0 0 3 0 0给你一个整数数组
nums,找到其中最长严格递增子序列的长度。
思路与算法
定义dp[i] 为考虑前 i 个元素,以第 i个数字结尾的最长上升子序列的长度,注意nums[i] 必须被选取。
我们从小到大计算dp 数组的值,在计算dp[i] 之前,我们已经计算出dp[0,…,i−1] 的值,则状态转移方程为:
即考虑往dp[0,…,i−1] 中最长的上升子序列后面再加一个 nums[i]。由于 dp[j] 代表nums[0,…,j] 中以nums[j] 结尾的最长上升子序列,所以如果能从 dp[j] 这个状态转移过来,那么nums[i] 必然要大于nums[j],才能将nums[i] 放在 nums[j] 后面以形成更长的上升子序列。
最后,整个数组的最长上升子序列即所有dp[i] 中的最大值。 $$ \text{LIS}_{\textit{length}}= \max(\textit{dp}[i]), \text{其中} , 0\leq i < n $$
# 时间复杂度:O(N^2)
class Solution:
def lengthOfLIS(self, nums):
if not nums:
return 0
dp = []
for i in range(len(nums)):
dp.append(1)
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
# 二分查找:O(NlogN),没太懂
class Solution(object):
def lengthOfLIS(self, nums):
# 定义新的列表
tails = [0] * len(nums)
# 定义已经插入的序列的长度
size = 0
for x in nums:
# 此处用二分查找,因为是排好序的序列,所以每次只与中间值比较
i, j = 0, size
while i != j:
m = (i + j) / 2
if tails[m] < x:
i = m + 1
else:
j = m
tails[i] = x
size = max(i + 1, size)
return size
# 输出序列,也没太懂
def lis(arr):
n = len(arr)
# m用来存储个数
m = [0]*n
# 序列从右到左,逐一比较
for x in range(n-2,-1,-1):
for y in range(n-1,x,-1):
if arr[x] < arr[y] and m[x] <= m[y]:
m[x] += 1
max_value = max(m)
result = []
for i in range(n):
if m[i] == max_value:
result.append(arr[i])
max_value -= 1
return result
arr = [0,1,0,3,2,3]
print(lis(arr))给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2] 输出:4 解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。 示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1] 输出:9
- 用哈希表存储每个端点值对应连续区间的长度
- 若数已在哈希表中:跳过不做处理
- 若是新数加入:
- 取出其左右相邻数已有的连续区间长度 left 和 right
- 计算当前数的区间长度为:cur_length = left + right + 1
- 根据 cur_length 更新最大长度 max_length 的值
- 更新区间两端点的长度值
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
hash_dict = dict()
max_length = 0
for num in nums:
if num not in hash_dict:
left = hash_dict.get(num - 1, 0)
right = hash_dict.get(num + 1, 0)
cur_length = 1 + left + right
if cur_length > max_length:
max_length = cur_length
hash_dict[num] = cur_length
hash_dict[num - left] = cur_length
hash_dict[num + right] = cur_length
return max_length给定一个整数数组
nums,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
此题与上一题思路一致:
在计算子序和dp[i] 之前,我们已经计算出前i-1个num的子序和dp[i−1] 值,那么对于第i个数num[i],要考虑原子序和dp[i−1]的值:
- 当dp[i−1]<=0时,不管num[i]为何值(>0,<0,=0),都要丢弃原来的计算值,重新计算,将dp[i]=num[i]时,当前i处为最大
- 当dp[i−1]>0时,当num[i]<0时,则dp[i]=num[i]+dp[i−1]导致dp[i]<dp[i−1],但是否小于0,未知,放入i+1时考虑;当num[i]>=0时,dp[i]=num[i]+dp[i−1]。综合起来,dp[i]=num[i]+dp[i−1]。
- 两种情况,综合为dp[i] = num[i] + max(dp[i−1], 0)
最后max(dp)
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if len(nums)==1:
return nums[0]
dp = []
dp.append(nums[0])
for i in range(1, len(nums), 1):
dp.append(nums[i] + max(dp[i-1],0))
return max(dp)
nums=[-2,1,-3,4,-1,2,1,-5,4]
s = Solution()
print(s.maxSubArray(nums))
# 优化为
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if len(nums)==1:
return nums[0]
for i in range(1, len(nums), 1):
nums[i] = nums[i] + max(dp[i-1],0)
return max(nums)给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
对于乘法,负数乘以负数,会变成正数,所以解题时需要维护两个变量,当前的最大值,以及最小值,最小值可能为负数,但没准下一步乘以一个负数,当前的最大值就变成最小值,而最小值则变成最大值了。
动态方程: $$ dp_{min}[i]=\min(dp_{max}[i-1] \times nums[i], nums[i], dp_{min}[i-1] \times nums[i]) \ dp_{max}[i]=\max(dp_{max}[i-1] \times nums[i], nums[i], dp_{min}[i-1] \times nums[i]) $$ 返回值max(dp_max)
class Solution(object):
def maxProduct(self, nums):
if len(nums)==1:
return nums[0]
dp_min = []
dp_max = []
dp_min.append(nums[0])
dp_max.append(nums[0])
for i in range(1, len(nums), 1):
dp_min.append(min(dp_min[i-1]*nums[i], dp_max[i-1]*nums[i], nums[i]))
dp_max.append(max(dp_min[i-1]*nums[i], dp_max[i-1]*nums[i], nums[i]))
return max(dp_max)你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
dp[i] = max(dp[i-2]+nums[i], dp[i-1]),只能隔一个抢
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums: return 0
dp, n = [0]*len(nums), len(nums)
dp[0] = nums[0]
for i in range(1, n):
dp[i] = max(dp[i-2]+nums[i], dp[i-1])
return dp[-1]你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2] 输出:3 解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
把环拆成两个队列,一个是从0到n-1,另一个是从1到n,然后返回两个结果最大的。
如上一题:
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums: return 0
n = len(nums)
if n <2: return nums[-1]
dp1, dp2 = [0]*(n-1), [0]*n
dp1[0] = nums[0]
dp2[1] = nums[1]
for i in range(1, n-1):
dp1[i] = max(dp1[i-2]+nums[i], dp1[i-1])
for i in range(2, n):
dp2[i] = max(dp2[i-2]+nums[i], dp2[i-1])
return max(dp1[-1], dp2[-1])在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
示例 1:
输入: [3,2,3,null,3,null,1]
3 / \ 2 3 \ \ 3 1输出: 7 解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: TreeNode) -> int:
res = self.dfs(root)
return max(res)
def dfs(self, root):
if not root: return [0, 0] # [偷当前节点金额,不偷当前节点金额]
left = self.dfs(root.left)
right = self.dfs(root.right)
val1 = root.val + left[1] + right[1] # 偷当前节点,不能偷子节点
val2 = max(left) + max(right) # 不偷当前节点,可偷可不偷子节点
return [val1, val2]给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11 输出:3 解释:11 = 5 + 5 + 1
背包的动态规划,就是取与不取的问题,
dp[i]表示金额为i需要最少的金额多少,
dp(n) = min(dp(n - c1), dp(n - c2), ... dp(n - cn)) + 1其中 c1 ~ cn 为硬币的所有面额。
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf') for _ in range(amount + 1)]
dp[0] = 0 # 当总金额为0时,最少硬币个数为0
for i in range(1, amount + 1):
for c in coins:
if i - c >= 0:
dp[i] = min(dp[i], dp[i - c] + 1)
# 当最小硬币个数为初始值时,代表不存在硬币组合能构成此金额
if dp[amount] == float('inf'):
return -1
else:
return dp[amount]给定数组 nums 由正整数组成,找到三个互不重叠的子数组的最大和。
每个子数组的长度为k,我们要使这3*k个项的和最大化。
返回每个区间起始索引的列表(索引从 0 开始)。如果有多个结果,返回字典序最小的一个。
示例:
输入: [1,2,1,2,6,7,5,1], 2 输出: [0, 3, 5] 解释: 子数组 [1, 2], [2, 6], [7, 5] 对应的起始索引为 [0, 3, 5]。 我们也可以取 [2, 1], 但是结果 [1, 3, 5] 在字典序上更大。
分两步解决这个问题
- 第一步:
- 1)计算出以 i 开头的 连续k个元素的和sum(nums[i:i+k]) 的和,用一个数组存起来sum_start_with=[]*len(nums) 存起来
- 2) 这个问题就变成了打家劫舍问题,相邻k个房子只能偷一家,最多只能偷三次,sum_start_with就是每个房子能偷的钱,看看最多能偷多少钱
- 第二步:反向找到偷了哪几家人的钱
class Solution:
def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:
#第一步
m = len(nums)
sum_start_with=[0]*m
sum_start_with[0]=sum(nums[:k])
for i in range(1,m-k+1):
sum_start_with[i]=sum_start_with[i-1]+nums[i+k-1]-nums[i-1]
# 初始化条件
dp = [[0]*4 for _ in range(m)]
dp[0][2]=sum_start_with[0]
#开始dp
for i in range(1,k):
dp[i][2] = max(dp[i-1][2],dp[i-1][3]+sum_start_with[i])
for i in range(k,m):
for j in range(2,-1,-1):
dp[i][j] = max(dp[i-1][j],dp[i-k][j+1]+sum_start_with[i])
# 第二步
ans = [0,0,0]
j=0
i = m-2
while i>=0:
if dp[i+1][j] != dp[i][j] :
ans[j]=i+1
j+=1
i-=k-1
i-=1
return ans[::-1]给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
思路:动态规划
- 记录【今天之前买入的最小值】
- 计算【今天之前最小值买入,今天卖出的获利】,也即【今天卖出的最大获利】
- 比较【每天的最大获利】,取最大值即可
前$i$天的最大收益 = max(前$i-1$天的最大收益,当前价格-前$i-1$天的最低价)
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if len(prices)<1:
return 0
get_max = 0
min_p = prices[0]
for p in prices[1:]:
min_p = min(p, min_p)
get_max = max(get_max, p - min_p)
return get_max给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [7,1,5,3,6,4] 输出: 7 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
要盈利,就要prices[i] - prices[i-1]>0,找出所有大于0的即可。
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
ans = []
for i in range(1, len(prices)):
if prices[i] - prices[i-1]>0:
ans.append(prices[i] - prices[i-1])
return sum(ans) if ans else 0给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。 随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
标准的三维DP动态规划,三个维度,第一维表示天,第二维表示交易了几次,第三维表示是否持有股票。与下面188题买卖股票4一样的代码,把交易k次定义为2次。当然也可以把内层的for循环拆出来,分别列出交易0次、1次、2次的状态转移方程即可.
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if not prices: return 0
n = len(prices)
dp = [[[0]*2 for _ in range(3)] for _ in range(n)]
for i in range(3):
# 第0天,不持有股票,持有股票
dp[0][i][0], dp[0][i][1] = 0, -prices[0]
# dp[i][j][0]表示第i天交易了j次时不持有股票, dp[i][j][1]表示第i天交易了j次时持有股票
for i in range(1, n):
for j in range(3):
if not j : # 不进行操作
dp[i][j][0] = dp[i-1][j][0]
else: # 进行买卖,最终不持有股票,可能是i-1天就不持有,可能是卖掉了
dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j-1][1]+prices[i])
# 进行买卖,最终持有股票,可能是i-1天就持有,可能是买了
dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j][0]-prices[i])
return max(dp[n-1][0][0], dp[n-1][1][0], dp[n-1][2][0])给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
class Solution(object):
def maxProfit(self, k, prices):
"""
:type k: int
:type prices: List[int]
:rtype: int
"""
if not prices: return 0
n = len(prices)
dp = [[[0]*2 for _ in range(k+1)] for _ in range(n)]
for i in range(k+1):
# 第0天,不持有股票,持有股票
dp[0][i][0], dp[0][i][1] = 0, -prices[0]
# dp[i][j][0]表示第i天交易了j次时不持有股票, dp[i][j][1]表示第i天交易了j次时持有股票
for i in range(1, n):
for j in range(k+1):
if not j : # 不进行操作
dp[i][j][0] = dp[i-1][j][0]
else: # 进行买卖,最终不持有股票,可能是i-1天就不持有,可能是卖掉了
dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j-1][1]+prices[i])
# 进行买卖,最终持有股票,可能是i-1天就持有,可能是买了
dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j][0]-prices[i])
return max([dp[n-1][i][0] for i in range(k+1)])老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。 评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果。 那么这样下来,老师至少需要准备多少颗糖果呢?
示例 1:
输入:[1,0,2] 输出:5 解释:你可以分别给这三个孩子分发 2、1、2 颗糖果。 示例 2:
输入:[1,2,2] 输出:4 解释:你可以分别给这三个孩子分发 1、2、1 颗糖果。 第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
局部最优可以推出全局最优。
正向:如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个,所以贪心:candy[i] = candy[i - 1] + 1。反向:candy[i-1] = max(candy[i] + 1, candy[i-1])。
class Solution(object):
def candy(self, ratings):
"""
:type ratings: List[int]
:rtype: int
"""
if not ratings: return 0
n = len(ratings)
candy = [1]*n
for i in range(1, n):
if ratings[i] > ratings[i-1]:
candy[i] = candy[i-1] + 1
for i in range(n-1, 0, -1):
if ratings[i] < ratings[i-1]:
candy[i-1] = max(candy[i] + 1, candy[i-1])
return sum(candy)给你一个字符串 s,找到 s 中最长的回文子串。
思路:双指针+动态规划
- 布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
- 子串跨越长度: L
判断情况:
- 如果长度L=1,一定为回文,则dp[i][j]=True
- 如果长度L=2,并且s[i]==s[j],也是回文,则dp[i][j]=True
- 如果长度L>2,则需要判断首首尾是否相同s[i]==s[j],且中间子串也是回文dp[i+1][j-1]=True,则dp[i][j]=True
class Solution(object):
def longestPalindrome(self, s):
n = len(s)
if n<2:
return s
dp =[[False]*n for _ in range(n)] # 变量dp
start, max_L = 0, 1 # 起始位与长度
for right in range(n):
for left in range(0, right+1):
L = right - left + 1
if L == 1: # 情况1
dp[left][right] = True
elif L ==2: # 情况2
dp[left][right] = s[left]==s[right]
else: # 情况3
dp[left][right] = dp[left+1][right-1] and s[left]==s[right]
if dp[left][right]: # 更新最大长度及起始位
if L > max_L:
max_L = L
start = left
return s[start:start+max_L]思路:双指针+中心点扩散
确定回文串,即找中心往两边扩散看是不是对称,而中心点有两种情况:一个元素,或两个元素。
class Solution(object):
def longestPalindrome(self, s):
def extend(i,j):
while 0<=i and j< len(s) and s[i]==s[j]: # 扩散的条件
i, j = i-1, j+1
return i,j
result = ''
for i in range(len(s)):
m, n = extend(i, i) # 一个元素扩散
result = s[m+1:n] if n-m-1 > len(result) else result
m, n = extend(i, i+1) # 两个元素扩散(如果两者相同)
result = s[m+1:n] if n-m-1 > len(result) else result
return result斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给你 n ,请计算 F(n) 。
# 递归是暴力搜索,也即会出现重复搜索即fib(n-1)在下一轮中即为fib(n-2),出现重复
class Solution(object):
def fib(self, n):
if n == 0 or n==1:
return n
else:
return self.fib(n-1) + self.fib(n-2)
# 动态规划
class Solution(object):
def fib(self, n):
if n == 0 or n==1:
return n
dp = [0 for _ in range(n+1)]
dp[0], dp[1] = 0, 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
输入:n = 4 输出:4 解释: T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4
动态规划,同上:
class Solution(object):
def tribonacci(self, n):
if n < 3:
return n if n<2 else 1
dp = [0 for _ in range(n+1)]
dp[0], dp[1], dp[2] = 0, 1, 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
return dp[n]假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
分析:
- 如果第一次爬的是1个台阶,那么剩下n-1个台阶,爬法是f(n-1)
- 如果第一次爬的是2个台阶,那么剩下n-2个台阶,爬法是f(n-2)
- 可以得出总爬法为: f(n) = f(n-1) + f(n-2)
- 只有一个台阶时f(1) = 1,只有两个台阶的时候 f(2) = 2
即为变相的斐波那契数。
class Solution(object):
def climbStairs(self, n):
if n < 2:
return n
dp = [0 for _ in range(n+1)]
dp[1], dp[2] = 1, 2
for i in range(3, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。
每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
示例 1:
输入:cost = [10, 15, 20] 输出:15 解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。
如上分析,只是增加了cost:
- 如果第一次爬的是1个台阶,那么剩下n-1个台阶,爬法是f(n-1)
- 如果第一次爬的是2个台阶,那么剩下n-2个台阶,爬法是f(n-2)
- 加上损失,爬法为: f(n) = min(cost(n-1)+f(n-1),cost(n-2) + f(n-2))
- 没有台阶时,自然为0,只有一个台阶时,不动f(1) = 0
class Solution(object):
def minCostClimbingStairs(self, cost):
n = len(cost)
if n<3:
return min(cost)
dp = [0 for _ in range(n+1)]
for i in range(2, n+1):
dp[i] = min(cost[i-1]+dp[i-1], cost[i-2]+dp[i-2])
return dp[n]一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

输入:m = 3, n = 7 输出:28
机器人一定会走m+n-2步,即从m+n-2中挑出m-1步向下走,即C((m+n-2),(m-1))。
class Solution(object):
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
dp = [[0]*(n) for _ in range(m)]
for i in range(0, m):
for j in range(0, n):
if i == 0 or j == 0:
dp[i][j] = 1
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?

网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出:2 解释: 3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
有障碍时,dp[i][j]=0
class Solution:
def uniquePathsWithObstacles(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
dp = [[0]*(n) for _ in range(m)]
for i in range(0, m):
for j in range(0, n):
if grid[i][j]==1: #
dp[i][j] = 0
else:
if i == 0 and j == 0:
dp[i][j] = 1
elif i==0:
dp[i][j]=dp[i][j-1]
elif j == 0:
dp[i][j]=dp[i-1][j]
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:

输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。
动态规划:dp[i][j] 代表[0, 0]位置到[i, j]位置的最小值
class Solution(object):
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
m, n = len(grid), len(grid[0])
dp = [[0]*(n) for _ in range(m)]
dp[0][0] = grid[0][0]
for i in range(1, m):
dp[i][0] = dp[i-1][0] + grid[i][0]
for j in range(1, n):
dp[0][j] = dp[0][j-1] + grid[0][j]
for i in range(1, m):
for j in range(1, n):
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
return dp[-1][-1]输出一条路径:
class Solution(object):
def minPathSum(self, grid):
m, n = len(grid), len(grid[0])
dp = [[0]*(n) for _ in range(m)]
dp[0][0] = grid[0][0]
for i in range(1, m):
dp[i][0] = dp[i-1][0] + grid[i][0]
for j in range(1, n):
dp[0][j] = dp[0][j-1] + grid[0][j]
for i in range(1, m):
for j in range(1, n):
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
res = []
res.append([m-1, n-1])
i, j = m-1, n-1
while not (i==0 and j==0):
if dp[i-1][j] < dp[i][j-1]:
i -= 1
else:
j -= 1
res.append([i,j])
return res[::-1]
ma = [[1,3,4,2,7],
[2,4,1,3,2],
[1,2,5,2,3],
[3,4,1,2,4],
[4,2,3,1,5]]
s = Solution()
print(s.minPathSum(ma))输出多条路径:
class Solution(object):
def minPathSum(self, grid):
m, n = len(grid), len(grid[0])
dp = [[0]*(n) for _ in range(m)]
dp[0][0] = grid[0][0]
for i in range(1, m):
dp[i][0] = dp[i-1][0] + grid[i][0]
for j in range(1, n):
dp[0][j] = dp[0][j-1] + grid[0][j]
for i in range(1, m):
for j in range(1, n):
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
'''
res: 最后的输出路径列表
tmp: 保存当前的一个路径
que: 存储当前存在的其他路径
tmp_ids: 存储当前路径在tmp的ids处开始出现分支
'''
res, tmp, que, tmp_ids = [], [], [], []
tmp.append([m-1, n-1])
i, j = m-1, n-1
while not (i==0 and j==0) or que:
if dp[i-1][j] == dp[i][j-1]:
que.append([i, j-1]) # 保存另一条路径
i = i-1
tmp_ids.append(len(tmp))# 保存分支点
elif dp[i-1][j] > dp[i][j-1]:
j = j-1
elif dp[i-1][j] < dp[i][j-1]:
i= i-1
tmp.append([i, j])
if i==0 and j==0:
res.append(tmp[::-1]) # 一条路径查找完成
if que:
tmp_id_list = tmp[:tmp_ids.pop()] # 取出已有路径的共同部分
tmp=tmp_id_list # 另一条分支的共同部分
i, j = que.pop() # 重新查找另一条路径
tmp.append([i, j])
return res
ma = [[1,1,2,2,8],
[1,4,1,3,8],
[2,1,5,2,8],
[3,4,1,2,1],
[8,8,8,1,2]]
s = Solution()
print(s.minPathSum(ma))一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
例如,考虑到如下布局的地下城,如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下,则骑士的初始健康点数至少为 7。
-2 (K) -3 3 -5 -10 1 10 30 -5 (P)
说明:
骑士的健康点数没有上限。
任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
最小耗费的生命值 表示骑士救完公主刚刚好死了所需要用的生命值,那么在终点时,已有的健康数-消耗的健康数=0,不死时,最少为1。如果我们要得到起始点的最小的耗费的生命值:
从其实起始点的右边、起始点的下边,两者之中选择一个耗费生命较小的,也就是二者之中的最优选择,然后算上本身这个格子所需要的血量,就是最小的耗费生命值了。
初始思路也是正序dp,此时dp[i][j]代表(0,0)到(i,j)的最低血量;但是实际递推时发现无法处理正健康值的网格,比如下一个网格是正健康值,则从起点到下一个网格的最低初始血量不变,但健康值发生了改变,dp数组无法记录与反映这一变化。
考虑倒序dp,此时dp[i][j]代表(i,j)到终点的最低血量,此时根据: 后一节点到达终点所需的最低血量(已知)、与当前节点的健康值(已知)倒推当前节点到达终点的最低血量(至少等于1):
即可改写为:
class Solution(object):
def calculateMinimumHP(self, dungeon):
"""
:type dungeon: List[List[int]]
:rtype: int
"""
m, n = len(dungeon), len(dungeon[0])
dp = [[0]*n for _ in range(m)]
# 终点初始条件
dp[-1][-1] = -dungeon[-1][-1]+1 if dungeon[-1][-1]<=0 else 1
# 初始化边界条件
for i in range(m-2, -1, -1):
dp[i][-1] = max(1, dp[i+1][-1] - dungeon[i][-1]) # 边界上,如果小于0,取1;大于0,取正值最大
for j in range(n-2, -1, -1):
dp[-1][j] = max(1, dp[-1][j+1] - dungeon[-1][j])
for i in range(m-2, -1, -1):
for j in range(n-2, -1, -1):
dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j]) # 转态转移公式
return dp[0][0]一个N x N的网格(grid) 代表了一块樱桃地,每个格子由以下三种数字的一种来表示:
0 表示这个格子是空的,所以你可以穿过它。 1 表示这个格子里装着一个樱桃,你可以摘到樱桃然后穿过它。 -1 表示这个格子里有荆棘,挡着你的路。 你的任务是在遵守下列规则的情况下,尽可能的摘到最多樱桃:
从位置 (0, 0) 出发,最后到达 (N-1, N-1) ,只能向下或向右走,并且只能穿越有效的格子(即只可以穿过值为0或者1的格子); 当到达 (N-1, N-1) 后,你要继续走,直到返回到 (0, 0) ,只能向上或向左走,并且只能穿越有效的格子; 当你经过一个格子且这个格子包含一个樱桃时,你将摘到樱桃并且这个格子会变成空的(值变为0); 如果在 (0, 0) 和 (N-1, N-1) 之间不存在一条可经过的路径,则没有任何一个樱桃能被摘到。 示例 1:
输入: grid = [[0, 1, -1], [1, 0, -1], [1, 1, 1]] 输出: 5 解释: 玩家从(0,0)点出发,经过了向下走,向下走,向右走,向右走,到达了点(2, 2)。 在这趟单程中,总共摘到了4颗樱桃,矩阵变成了[[0,1,-1],[0,0,-1],[0,0,0]]。 接着,这名玩家向左走,向上走,向上走,向左走,返回了起始点,又摘到了1颗樱桃。 在旅程中,总共摘到了5颗樱桃,这是可以摘到的最大值了。
思路的转换
- 这里要避免使用贪心法,比如保证单次路径最多的樱桃采摘,这样子对于两次结果反而不好的情况
- 既然一次不行,那么问题就变成按照两条路径一起找最优就可以
动态规划
-
定义
- 这里要考虑降维,对于两条路径同时走,假设现在是 x1,y1 和 x2,y2, 当前步数是s,俺么满足 x1+y1=x2+y2=s,这里表示我们可以对于 x1,y1,x2,y2只要至少
- 其中三个就可以退出另外一个
- d[x1][y1][x2] 表示对于目前起点到最后 [N-1,N-1]的最多的樱桃数量
-
初始化
- 因为我们计算是取最大值,默认可以把他们都设置为最小值 INT_MIN
-
计算 这里要考虑多种情况
- 如何避免重复计算,通过判断是否是初始值 INT_MIN 可以直接返回d的结果
- 如何返回无法找到的路径,可以设置一个 负数表示无效,如 -1,而我们数值最小是0,那么结果就是0
- 如果当前就是 N-1,N-1, 直接返回 grid[N-1][N-1] 的数值就是樱桃数量
- 其他情况,我们会有四个选择(每条路径两种走法,所以是2*2=4),然后取最大结果
- 选择1:路径1向右, 路径2向右
- 选择2:路径1向右,路径2向下
- 选择3:路径1向下, 路径2向右
- 选择4:路径1向下,路径2向下
- 计算下一格的数值需要判断去重,避免下一跳一样但是重复计算grid数值
- 计算从顶到底的计算方式
-
结果
- max(0, d[0][0][0]): 这里就是考虑可能找不到路径的情况 返回0
class Solution:
def cherryPickup(self, grid):
n = len(grid)
dp = [[[None for _ in range(n)] for _ in range(n)] for _ in range(n)]
def dfs(r1, c1, c2) -> int:
r2 = r1 + c1 - c2 #八皇后问题 左斜线 的特点 rc_sum为同一个值
if r1 == n or r2 == n or c1 == n or c2 == n or grid[r1][c1] == -1 or grid[r2][c2] == -1: #超范围了 或者是荆棘
return float('-inf')
elif r1 == c1 == n-1: #到右下的终点了
return grid[r1][c1]
elif dp[r1][c1][c2] is not None: #访问过了 计算过了 就不用再算了 直接返回
return dp[r1][c1][c2]
else:
res = grid[r1][c1]
if c1 != c2:
res += grid[r2][c2]
res += max(dfs(r1, c1+1, c2+1), dfs(r1, c1+1, c2), dfs(r1+1, c1, c2), dfs(r1+1, c1, c2+1)) #右右 右下 下下 下右
dp[r1][c1][c2] = res
return res
return max(0, dfs(0, 0, 0))在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:

输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出:4
dp[i][j]表示以第i行第j列为右下角所能构成的最大正方形边长。当我们判断以某个点为正方形右下角时最大的正方形时,那它的上方,左方和左上方三个点也一定是某个正方形的右下角,否则该点为右下角的正方形最大就是它自己了,则递推式为,相邻三个矩形边长的最小值+1:
class Solution(object):
def maximalSquare(self, matrix):
"""
:type matrix: List[List[str]]
:rtype: int
"""
if not matrix: return 0
m, n = len(matrix), len(matrix[0])
dp = [[0]*n for _ in range(m)]
for i in range(m):
for j in range(n):
if matrix[i][j] == "1":
dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])
return max(max(it) for it in dp)**2在一个大小在 (0, 0) 到 (N-1, N-1) 的2D网格 grid 中,除了在 mines 中给出的单元为 0,其他每个单元都是 1。网格中包含 1 的最大的轴对齐加号标志是多少阶?返回加号标志的阶数。如果未找到加号标志,则返回 0。
一个 k" 阶由 1 组成的“轴对称”加号标志具有中心网格 grid[x][y] = 1 ,以及4个从中心向上、向下、向左、向右延伸,长度为 k-1,由 1 组成的臂。下面给出 k" 阶“轴对称”加号标志的示例。注意,只有加号标志的所有网格要求为 1,别的网格可能为 0 也可能为 1。
k 阶轴对称加号标志示例: 阶 1: 000 010 000 阶 2: 00000 00100 01110 00100 00000 阶 3: 0000000 0001000 0001000 0111110 0001000 0001000 0000000 示例 1: 输入: N = 5, mines = [[4, 2]] 输出: 2 解释: 11111 11111 11111 11111 11011 在上面的网格中,最大加号标志的阶只能是2。一个标志已在图中标出。
因为判断是否形成加法标志需要上、下、左、右四个臂的长度,所以不能单一的变量表示不了这个状态;所以考虑用四个变量表示状态,分别为上、下、左、右的连续臂展长度;
- 上、左状态变量在正序遍历数组的时候确定,下、右状态变量用逆序遍历数组的时候确定;
- 状态转移方程为 dp[i+1][j+1][0]=dp[i][j+1][0]+1 (上状态);
- 最后加法的阶数为四个状态中最下的那个确定;
class Solution:
def orderOfLargestPlusSign(self, N, mines):
matrix=[[1]*N for _ in range(N)]
for i in mines:
matrix[i[0]][i[1]]=0
dp = [[[0,0,0,0] for _ in range(N+2)] for _ in range(N+2)]
for i in range(N): #先正向遍历
for j in range(N):
if matrix[i][j]==1:
dp[i+1][j+1][0]=dp[i][j+1][0]+1 # 上
dp[i+1][j+1][1]=dp[i+1][j][1]+1 # 左
for i in range(N-1,-1,-1):
for j in range(N-1,-1,-1): #逆向遍历
if matrix[i][j]==1:
dp[i + 1][j + 1][2] = dp[i+2][j + 1][2]+1 # 下
dp[i + 1][j + 1][3] = dp[i + 1][j+2][3]+1 # 右
m=max([max([min(i) for i in it]) for it in dp])
return m给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出:6
思路:
- 遍历矩阵中的每一个元素,计算“以该点为右下角顶点的矩形的最大面积”;
- 为了方便理解,这里使用最直接的方式计算矩形面积:使用状态数组维护高度(height),遍历所有有效的宽度(width)。
代码:
- height数组保存matrix[i][j]位置的高度
- 遍历矩阵中的每一个元素,将该点视为右下角顶点
- 通过height数组获得高度、不断遍历有效的宽度以计算面积
解代码状态转移方程:
可以看到,每一个元素的值,仅与上一行元素有关,故做出以下优化:
height数组降维,仅保存当前行的元素的高度- 取消初始化步骤,在使用前进行初始化
class Solution:
def maxmalRectangle(self , matrix):
m, n = len(matrix), len(matrix[0])
maxarea = 0
dp = [[0]*n for _ in range(m)]
for i in range(m): # 遍历每一行
for j in range(n): # 遍历每一列
if matrix[i][j] == 0:
continue
# j=0时,是初始列,其他列递归
height = dp[i][j] = dp[i][j-1] + 1 if j else 1
for k in range(i,-1,-1): # 倒序遍历每一行
height = min(height , dp[k][j]) # 最小高度(同一列 上下几行的最小【最大高度】)
maxarea = max(maxarea , height*(i - k + 1)) # 同一列上下几行的最小【最大高度】*行数=当前行最大面积
return maxarea我们把玻璃杯摆成金字塔的形状,其中第一层有1个玻璃杯,第二层有2个,依次类推到第100层,每个玻璃杯(250ml)将盛有香槟。
从顶层的第一个玻璃杯开始倾倒一些香槟,当顶层的杯子满了,任何溢出的香槟都会立刻等流量的流向左右两侧的玻璃杯。当左右两边的杯子也满了,就会等流量的流向它们左右两边的杯子,依次类推。(当最底层的玻璃杯满了,香槟会流到地板上)
例如,在倾倒一杯香槟后,最顶层的玻璃杯满了。倾倒了两杯香槟后,第二层的两个玻璃杯各自盛放一半的香槟。在倒三杯香槟后,第二层的香槟满了 - 此时总共有三个满的玻璃杯。在倒第四杯后,第三层中间的玻璃杯盛放了一半的香槟,他两边的玻璃杯各自盛放了四分之一的香槟,如下图所示。

现在当倾倒了非负整数杯香槟后,返回第 i 行 j 个玻璃杯所盛放的香槟占玻璃杯容积的比例(i 和 j都从0开始)。
示例 1: 输入: poured(倾倒香槟总杯数) = 1, query_glass(杯子的位置数) = 1, query_row(行数) = 1 输出: 0.0 解释: 我们在顶层(下标是(0,0))倒了一杯香槟后,没有溢出,因此所有在顶层以下的玻璃杯都是空的。
示例 2: 输入: poured(倾倒香槟总杯数) = 2, query_glass(杯子的位置数) = 1, query_row(行数) = 1 输出: 0.5 解释: 我们在顶层(下标是(0,0)倒了两杯香槟后,有一杯量的香槟将从顶层溢出,位于(1,0)的玻璃杯和(1,1)的玻璃杯平分了这一杯香槟,所以每个玻璃杯有一半的香槟。
模拟过程:
class Solution:
def champagneTower(self, poured, query_row, query_glass):
n=query_row
dp=[[0]*(n+1) for _ in range(n+1)]
dp[0][0]=poured
for i in range(n):
for j in range(n+1):
if dp[i][j]>1:
dp[i+1][j]+=(dp[i][j]-1)/2
dp[i+1][j+1]+=(dp[i][j]-1)/2
dp[i][j]=1
# 不要忘记和1取min
return min(1,dp[query_row][query_glass])给定一个正整数政组,最大为100个成员,从第一个成员开始,去到政组最后一个成品最少的步囊政,第一步必须从第一元素开始,1<=步长<len/2,第二步开始以所在成员的数字走相应的步数,如果目标不可达返回-1,只绘出最少的步获敌量 编入描述: 由正整数组成的基组,以空格分隔,数组长度小于100,请自行解析数据数量。 输出描述: 正整数,表示最少的步数,如果不存在输出-1 示例1 输入
7 5 9 4 2 6 8 3 5 4 3 9
输出
2
num_list = list(map(int, input().strip().split(' ')))
N = len(num_list)
step = 1
res = N
Flag = False
while step < (N/2):
idx = 0
tmp_step = step
cnt = 0
while (idx + tmp_step) < N:
idx +=tmp_step
if idx == (N-1):
Flag = True
tmp_step = num_list[idx]
cnt += 1
if Flag:
res = min(res, cnt)
step += 1
if Flag:
print(res)
else:
print(-1)目标是找到矩阵中 “岛屿的数量” ,上下左右相连的 1 都被认为是连续岛屿。
深度优先dfs方法: 设目前指针指向一个岛屿中的某一点 (i, j),寻找包括此点的岛屿边界。
- 从 (i, j) 向此点的上下左右 (i+1,j),(i-1,j),(i,j+1),(i,j-1) 做深度搜索。
- 终止条件:
- (i, j) 越过矩阵边界;
- grid[i][j] == 0,代表此分支已越过岛屿边界。
- 搜索岛屿的同时,执行 grid[i][j] = '0',即将岛屿所有节点删除,以免之后重复搜索相同岛屿。
主循环:
- 遍历整个矩阵,当遇到 grid[i][j] == '1' 时,从此点开始做深度优先搜索 dfs,岛屿数 count + 1 且在深度优先搜索中删除此岛屿。
- 最终返回岛屿数 count 即可。
class Solution(object):
def numIslands(self, grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
count=0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j]=='1': # 当有陆地时,深度搜索,直到满足边界,搜取完全后加1
self.dfs(grid, i, j)
count +=1
return count
def dfs(self, grid, i, j):
# 边界条件
if not (0<=i<len(grid)) or not (0<=j<len(grid[0])) or grid[i][j]=='0': return
# 将搜素过的标记为'0'
grid[i][j]='0'
# 向其他四个方向搜索
self.dfs(grid, i-1, j)
self.dfs(grid, i+1, j)
self.dfs(grid, i, j-1)
self.dfs(grid, i, j+1)
grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
s = Solution()
print(s.numIslands(grid))广度优先遍历 BFS
主循环和思路一类似,不同点是在于搜索某岛屿边界的方法不同。
bfs 方法:
- 借用一个队列 queue,判断队列首部节点 (i, j) 是否未越界且为 1:
- 若是则置零(删除岛屿节点),并将此节点上下左右节点 (i+1,j),(i-1,j),(i,j+1),(i,j-1) 加入队列;
- 若不是则跳过此节点;
- 循环 pop 队列首节点,直到整个队列为空,此时已经遍历完此岛屿。
class Solution:
def numIslands(self, grid):
def bfs(grid, i, j):
queue = [[i, j]]
while queue:
[i, j] = queue.pop(0) # 弹出第一个
# 判断是否满足加入队列的条件
if 0 <= i < len(grid) and 0 <= j < len(grid[0]) and grid[i][j] == '1':
grid[i][j] = '0'
queue += [[i + 1, j], [i - 1, j], [i, j - 1], [i, j + 1]] # 增加周边搜索
count = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == '1':
bfs(grid, i, j)
count += 1
return count
grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
s = Solution()
print(s.numIslands(grid))给定一个非空01二维数组表示的网格,一个岛屿由四连通(上、下、左、右四个方向)的 1 组成,你可以认为网格的四周被海水包围。
请你计算这个网格**有多少个形状不同的岛屿。 两个岛屿被认为是相同的,当且仅当一个岛屿可以通过平移变换(不可以旋转、翻转)和另一个岛屿重合。
样例 1: 11000 11000 00011 00011 给定上图,返回结果 1。 样例 2: 11011 10000 00001 11011 给定上图,返回结果 3。 注意: 11 1 和 1 11 是不同的岛屿,因为我们不考虑旋转、翻转操作。 注释 : 二维数组每维的大小都不会超过50。
考虑去重,一般都会考虑集合set(),那么只需要在原来的基础上,保留相对路径即可,最后再用set()去重,输出集合元素的个数即可。
class Solution(object):
def numDistinctIslands(self, grid):
shape = set()
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j]==1:
self.start = [i,j] # 岛屿的起始点
self.path = [] # 保存岛屿的路径
self.dfs(grid, i, j)
shape.add(tuple(self.path)) # 将路径加入集合中
return len(shape)
def dfs(self, grid, i, j):
if not (0<=i<len(grid)) or not (0<=j<len(grid[0])) or grid[i][j]==0: return
grid[i][j]=0
self.path.append((i -self.start[0], j-self.start[1])) # 保存相对路径
self.dfs(grid, i-1, j)
self.dfs(grid, i+1, j)
self.dfs(grid, i, j-1)
self.dfs(grid, i, j+1)
grid = [
[1, 1, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 1],
[0, 1, 0, 1, 1, 1]
]
s = Solution()
print(s.numDistinctIslands(grid)) 给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
在岛屿问题的基础上,添加计数功能。
class Solution(object):
def maxAreaOfIsland(self, grid):
max_num=0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j]==1: # 当有陆地时,深度搜索,直到满足边界,搜取完全后加1
max_num = max(self.dfs(grid, i, j), max_num)
return max_num
def dfs(self, grid, i, j):
# 边界条件
if not (0<=i<len(grid)) or not (0<=j<len(grid[0])) or grid[i][j]==0: return 0
# 将搜素过的标记为'0'
grid[i][j]=0
count = 1
# 向其他四个方向搜索
count += self.dfs(grid, i-1, j)
count += self.dfs(grid, i+1, j)
count += self.dfs(grid, i, j-1)
count += self.dfs(grid, i, j+1)
return count在给定的二维二进制数组 A 中,存在两座岛。(岛是由四面相连的 1 形成的一个最大组。)
现在,我们可以将 0 变为 1,以使两座岛连接起来,变成一座岛。
返回必须翻转的 0 的最小数目。(可以保证答案至少是 1 。)
示例 1:
输入:A = [[0,1],[1,0]] 输出:1 示例 2:
输入:A = [[0,1,0],[0,0,0],[0,0,1]] 输出:2 示例 3:
输入:A = [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]] 输出:1
提示:
2 <= A.length == A[0].length <= 100A[i][j] == 0或A[i][j] == 1
- 遍历数组找到第一个为1的数
- 以当前为1的坐标为起点进行深度优先搜索,找到第一个岛屿的全部范围,注意,每找到一个点要标记一下,将搜索过的点的值改为-1,以免重复寻找
- 以第一个岛屿的所有坐标为起点,进行广度优先搜索,找到不属于该岛的第一个1,返回到达该点所搜索的次数,就为最短的桥,注意,找过的点也要标记一下,以免重复寻找
class Solution(object):
def shortestBridge(self, A):
"""
:type A: List[List[int]]
:rtype: int
"""
n, queue = len(A), []
# 深度优先搜索
def dfs(x,y):
A[x][y] = -1
queue.append((x,y))
for i, j in [(x+1, y), (x-1, y), (x, y+1), (x, y-1)]:
if 0<=i<n and 0<=j<n and A[i][j] == 1:
dfs(i, j)
def find_first_island():
for i in range(n):
for j in range(n):
if A[i][j] == 1:
dfs(i,j)
return
find_first_island()
count = 0
# 广度优先搜索
while queue:
t = []
for x, y in queue:
for i, j in [(x+1, y), (x-1, y), (x, y+1), (x, y-1)]:
if 0<=i<n and 0<=j<n:
if A[i][j]==1:
return count
elif A[i][j]==0:
A[i][j] = -1
t.append((i, j))
count += 1
queue = t
return count在一张大小为row*col的方格区域地图上,处处暗藏杀机,地图上每一个格子上均有一个倒计时装置,当时间变为0时会触发机关,使得该格子区域变为一处死地,该区域无法通过,英雄每移动一个格子消耗1s。英雄可以向上下左右四个方向移动,请你设置一条最佳线路,让英雄以最快的速度从起点[0,0]逃到出口[row-1, col-1]离开。注意:英雄在出生点和出口时,该区域不能为死地。
输入描述:
- 首行输入以单个空格分割的两个正整数row和col, row代表地图行数(0<rowK<= 15), col代表地图列数(0< col <=15);
- 接下来row行,每一行包含col个以单个空格分割的数字,代表对应格子区域倒置时装置设定时间time(单位为s)(0<= tirme<= 100)。
输出描述:
接下来row行,每一行包含col个以单个空格分割的数字,代表对应格子区域倒置时装置设定时间time(单位为s)(0<= tirme<= 100)。
例如:
matrix = [ [3,5,4,2,3], [4,2,3,4,3], [4,3,4,3,2], [2,5,3,2,3], [5,3,4,3,3]]
输出:-1
最短路径,宽度优先搜索:
m, n = list(map(int, input().strip().split()))
matrix = []
while True:
try:
tmp = list(map(int, input().strip().split()))
matrix.append(tmp)
except EOFError:
break
m, n = len(matrix), len(matrix[0])
if matrix[-1][-1] < m or matrix[-1][-1] < n:
print(-1)
queue = set() # 保存扩展方向、路径
queue.add((0, 0))
count = 0
Flag = False
matrix = [list(map(lambda x: x+1, it)) for it in matrix]
while queue and (not Flag):
t = set()
count += 1
matrix = [list(map(lambda x: x-1 if x>=1 else 0, it)) for it in matrix] # 定时装置,元素值更新
if matrix[-1][-1] == 0: # 终点已无时间,退出
break
for x, y in queue: # 每个点,各方向扩展路径
for i, j in [(x+1, y), (x-1, y), (x, y+1), (x, y-1)]:
if 0<=i<m and 0<=j<n: # 扩展路径的约束
if matrix[i][j] > 0:
if i == (m-1) and j ==(n-1) : # 达到终点
Flag = True
break
else:
t.add((i, j)) # 未达到终点,扩展路径
queue = t
if not queue or matrix[-1][-1] == 0: # 提前退出
print(-1)
if Flag: # 输出步数
print(count)树的递归模板:
- 终止条件:什么时候递归到头了?此题自然是root为空的时候,空树当然是平衡的。
- 思考返回值,每一级递归应该向上返回什么信息?
- 单步操作应该怎么写?因为递归就是大量的调用自身的重复操作,因此从宏观上考虑,只用想想单步怎么写就行了,左树和右树应该看成一个整体,即此时树一共三个节点:root,root.left,root.right。
给定一个二叉树,返回其节点值的锯齿形层序遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
首先需实现二叉树的层序遍历,后对层序遍历时的层数进行判断:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def zigzagLevelOrder(self, root):
def helper(node, level):
if not node:
return
else:
if level%2==1:
sol[level-1].append(node.val) # 类似于堆栈,从右侧推入
else:
sol[level-1].insert(0, node.val) # 类似于堆栈,从左侧推入
if len(sol) == level: # 遍历到新层时,只有最左边的结点使得等式成立
sol.append([])
helper(node.left, level+1)
helper(node.right, level+1)
sol = [[]]
helper(root, 1)
return sol[:-1]
if __name__ == '__main__':
tree = TreeNode(0)
tree.left = TreeNode(1)
tree.right = TreeNode(2)
tree.left.left = TreeNode(3)
tree.left.right = TreeNode(4)
tree.right.left = TreeNode(5)
tree.right.right = TreeNode(6)
s = Solution()
print(s.levelOrder(tree)) class Solution(object):
def levelOrder(self, root):
def helper(node, level):
if not node:
return
else:
result[level-1].append(node.val)
if len(result)==level:
result.append([])
helper(node.left, level+1)
helper(node.right, level+1)
result=[[]]
helper(root, 1)
return result[:-1]199-二叉树的右视图(左右上下视图)
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
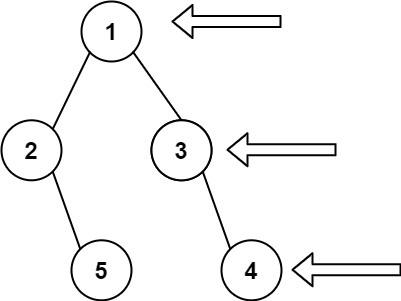
输入: [1,2,3,null,5,null,4] 输出: [1,3,4] 示例 2:
输入: [1,null,3] 输出: [1,3]
即是层序遍历的最后一个节点值,按照层序遍历即可。
import pprint
class Solution(object):
def rightSideView(self, root):
def helper(node, level):
if not node:
return
else:
result[level-1].append(node.val)
if len(result)==level:
result.append([])
helper(node.left, level+1)
helper(node.right, level+1)
result=[[]]
helper(root, 1)
return [it[-1] for it in result[:-1]]同理左视图即为每一层的第一个值。
import pprint
class Solution(object):
def rightSideView(self, root):
def helper(node, level):
if not node:
return
else:
result[level-1].append(node.val)
if len(result)==level:
result.append([])
helper(node.left, level+1)
helper(node.right, level+1)
result=[[]]
helper(root, 1)
return [it[0] for it in result[:-1]]俯视图:
以root节点,建立坐标,左侧宽度wide递减,右侧宽度wide递增,向下深度deep递增,每一个值,均有一个宽度和深度坐标。那么俯视图,则是同一宽度值下,深度最前的那个。
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def zigzagLevelOrder(self, root):
def helper(node, deep, wide):
if not node: return
if wide not in dic.keys(): # 保存节点值
dic[wide] = [node.val, deep]
elif dic[wide][1]>deep: # 如果当前宽度值更小,则更新
dic[wide] = [node.val, deep]
helper(node.left, deep+1, wide-1)
helper(node.right, deep+1, wide+1)
dic = {} # 字典保存数据及坐标,key为宽度,因为最后按宽度从小到大输出
helper(root, 0, 0)
# 按宽度从小到大输出节点值
return [dic[it][0] for it in sorted(dic.keys())]
if __name__ == '__main__':
tree = TreeNode(2)
tree.left = TreeNode(7)
tree.right = TreeNode(5)
tree.left.left = TreeNode(2)
tree.left.right = TreeNode(6)
tree.left.right.left = TreeNode(5)
tree.left.right.right = TreeNode(11)
tree.right.right = TreeNode(9)
tree.right.right.left = TreeNode(4)
s = Solution()
print(s.zigzagLevelOrder(tree)) 那么仰视图,则相反,输出宽度值下的,深度最大的那个节点值。
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def zigzagLevelOrder(self, root):
def helper(node, deep, wide):
if not node: return
if wide not in dic.keys():
dic[wide] = [node.val, deep]
elif dic[wide][1]<=deep: # 深度值更新
dic[wide] = [node.val, deep]
helper(node.left, deep+1, wide-1)
helper(node.right, deep+1, wide+1)
dic = {}
helper(root, 0, 0)
return [dic[it][0] for it in sorted(dic.keys())]
if __name__ == '__main__':
tree = TreeNode(2)
tree.left = TreeNode(7)
tree.right = TreeNode(5)
tree.left.left = TreeNode(2)
tree.left.right = TreeNode(6)
tree.left.right.left = TreeNode(5)
tree.left.right.right = TreeNode(11)
tree.right.right = TreeNode(9)
tree.right.right.left = TreeNode(4)
s = Solution()
print(s.zigzagLevelOrder(tree)) 较为简单。
class Solution(object):
def inorderTraversal(self, root):
if not root:
return []
return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。 节点的右子树只包含 大于 当前节点的数。 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

输入:root = [2,1,3] 输出:true 示例 2:
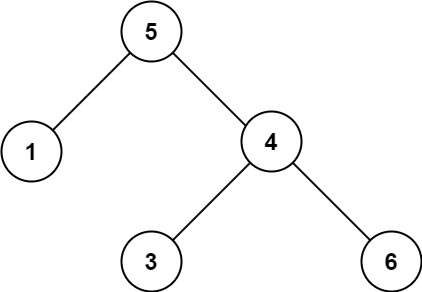
输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
res = []
def dfs(root):
if not root: return
dfs(root.left)
res.append(root.val)
dfs(root.right)
dfs(root)
return res == sorted(res) and len(set(res)) == len(res) #检查list里的数有没有重复元素,以及是否按从小到大排列给定一个 N 叉树,返回其节点值的 后序遍历 。
N 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
进阶:
递归法很简单,你可以使用迭代法完成此题吗?
示例 1:

输入:root = [1,null,3,2,4,null,5,6] 输出:[5,6,3,2,4,1]
"""
# Definition for a Node.
class Node(object):
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution(object):
def postorder(self, root):
"""
:type root: Node
:rtype: List[int]
"""
ans = []
def dfs(root):
if not root: return None
for it in root.children:
dfs(it)
ans.append(root.val)
dfs(root)
return ans给定一个 N 叉树,返回其节点值的 前序遍历 。
N 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
进阶:
递归法很简单,你可以使用迭代法完成此题吗?
示例 1:

输入:root = [1,null,3,2,4,null,5,6] 输出:[1,3,5,6,2,4]
"""
# Definition for a Node.
class Node(object):
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution(object):
def preorder(self, root):
"""
:type root: Node
:rtype: List[int]
"""
ans = []
def dfs(root):
if not root: return None
ans.append(root.val)
for it in root.children:
dfs(it)
dfs(root)
return ans给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:

输入:root = [1,null,3,2,4,null,5,6] 输出:[[1],[3,2,4],[5,6]]
"""
# Definition for a Node.
class Node(object):
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution(object):
def levelOrder(self, root):
"""
:type root: Node
:rtype: List[List[int]]
"""
ans = [[]]
def dfs(root, level):
if not root: return None
ans[level-1].append(root.val)
if len(ans)==level: ans.append([])
for it in root.children:
dfs(it, level+1)
dfs(root, 1)
return ans[:-1]翻转一棵二叉树。
示例:
输入:
4 / \ 2 7 / \ / \ 1 3 6 9输出:
4 / \ 7 2 / \ / \9 6 3 1
# 前序遍历
class Solution(object):
def invertTree(self, root):
if root is None: return
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
class Solution(object):
def invertTree(self, root):
if root is None: return
stack = [root]
while stack:
cur = stack.pop()
cur.left, cur.right = cur.right, cur.left
if cur.right:
stack.append(cur.right)
if cur.left:
stack.append(cur.left)
return root
# 中序遍历
class Solution(object):
def invertTree(self, root):
if root is None: return
self.invertTree(root.left)
root.left, root.right = root.right, root.left
self.invertTree(root.left)
return root
class Solution(object):
def invertTree(self, root):
if root is None: return
stack, cur = [], root
while stack or cur:
if cur:
stack.append(cur)
cur = cur.left
else:
tmp = stack.pop()
tmp.left, tmp.right = tmp.right, tmp.left
cur = tmp.left
return root
# 后序遍历
class Solution(object):
def invertTree(self, root):
if root is None: return
self.invertTree(root.left)
self.invertTree(root.right)
root.left, root.right = root.right, root.left
return root
class Solution(object):
def invertTree(self, root):
if root is None: return
stack, mark_node, cur = [], None, root
while stack or cur:
if cur:
stack.append(cur)
cur = cur.left
elif stack[-1].right != mark_node:
cur = stack[-1].right
mark_node = None
else:
mark_node = stack.pop()
mark_node.left, mark_node.right = mark_node.right, mark_node.left
return root
# 层序遍历
class Solution(object):
def invertTree(self, root):
def helper(node, level):
if not node:
return
else:
sol[level-1].append(node.val)
node.left, node.right = node.right, node.left
if len(sol) == level:
sol.append([])
helper(node.left, level+1)
helper(node.right, level+1)
sol = [[]]
helper(root, 1)
return root
class Solution(object):
def invertTree(self, root):
if root is None: return
curr, queue = root, [root]
while queue:
curr = queue.pop(0) #弹出根节点
curr.left, curr.right = curr.right, curr.left
if curr.left: # 将左右节点加入队列中
queue.append(curr.left)
if curr.right:
queue.append(curr.right)
return root给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
- 输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
- 输出:3
- 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
两个节点 p,q 分为两种情况:
- p 和 q 在相同子树中
- p 和 q 在不同子树中
从根节点遍历,递归向左右子树查询节点信息
递归终止条件:如果当前节点为空或等于 p 或 q,则返回当前节点
- 递归遍历左右子树,如果左右子树查到节点都不为空,则表明 p 和 q 分别在左右子树中,因此,当前节点即为最近公共祖先;
- 如果左右子树其中一个不为空,则返回非空节点。
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
if root==p or root==q or not root: return root
left = self.lowestCommonAncestor(root.left, p, q) #遍历左子树
right = self.lowestCommonAncestor(root.right, p, q) #遍历右子树
if left and right: return root # 左右不空,返回当前节点
return right if right else left # 代替如下几行
# if not left and right:
# return right
# elif not right and left:
# return left
# else:
# return None根据一棵树的前序遍历与中序遍历构造二叉树。
注意:你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7]返回如下的二叉树:
3 / \ 9 20 / \ 15 7
前序遍历:根节点->左子树->右子树**(根->左->右)**,即(root.val)[左子树的结点的数值们,长度为left_len] [右子树的结点的数值们,长度为right_len]
中序遍历:左子树->根节点->右子树**(左->根->右)**,即[左子树的结点的数值们,长度为left_len] (root.val)[右子树的结点的数值们,长度为right_len]
进一步分析:
- 前序中左起第一位
1肯定是根结点,我们可以据此找到中序中根结点的位置rootin; - 中序中根结点左边就是左子树结点,右边就是右子树结点,即
[左子树结点,根结点,右子树结点],我们就可以得出左子树结点个数为int left = rootin - leftin;; - 前序中结点分布应该是:
[根结点,左子树结点,右子树结点]; - 根据前一步确定的左子树个数,可以确定前序中左子树结点和右子树结点的范围;
- 如果我们要前序遍历生成二叉树的话,下一层递归应该是:
- 左子树:
root.left = pre_order(前序左子树范围,中序左子树范围); - 右子树:
root.right = pre_order(前序右子树范围,中序右子树范围);。
- 左子树:
- 每一层递归都要返回当前根结点
root;
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution(object):
def buildTree(self, preorder, inorder):
if not inorder:
return None
root = TreeNode(preorder[0]) # 根节点
mid = inorder.index(preorder[0]) # 中序中的节点位置
root.left = self.buildTree(preorder[1:mid+1], inorder[:mid]) # 递归左子树
root.right = self.buildTree(preorder[mid+1:], inorder[mid+1:]) # 递归右子树
return root根据一棵树的中序遍历与后序遍历构造二叉树。
注意:你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3]返回如下的二叉树:
3 / \ 9 20 / \ 15 7
中序遍历:左子树->根节点->右子树**(左->根->右)**,即[左子树的结点的数值们,长度为left_len] (root.val)[右子树的结点的数值们,长度为right_len]
后序遍历:左子树->右子树->根节点**(左->右->根)**,即[左子树的结点的数值们,长度为left_len] [右子树的结点的数值们,长度为right_len](root.val)
进一步分析(类似上一题思路):
- 后序中左起最后一位肯定是根结点,我们可以据此找到中序中根结点的位置
rootin; - 中序中根结点左边就是左子树结点,右边就是右子树结点,即
[左子树结点,根结点,右子树结点],我们就可以得出左子树结点个数为int left = rootin - leftin;; - 后序中结点分布应该是:
[左子树结点,右子树结点,根结点]; - 根据前一步确定的左子树个数,可以确定后序中左子树结点和右子树结点的范围;
- 如果我们要后序遍历生成二叉树的话,下一层递归应该是:
- 左子树:
root.left = post_order(中序左子树范围, 后序左子树范围); - 右子树:
root.right = post_order(中序右子树范围, 后序右子树范围);。
- 左子树:
- 每一层递归都要返回当前根结点
root;
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution(object):
def buildTree(self, inorder, postorder):
if not postorder:
return None
root = TreeNode(postorder[-1])
mid = inorder.index(postorder[-1])
root.left = self.buildTree(inorder[:mid], postorder[:mid]) # mid是否加1,可以根据例子而得
root.right = self.buildTree(inorder[mid+1:], postorder[mid:-1])
return root给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树 [3,9,20,null,null,15,7],
3 / \ 9 20 / \ 15 7返回它的最大深度 3 。
按照递归的模板写即可:
class Solution(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0 # 到达根节点,返回0
# 左右子树,取最大深度
return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1由于递归中,存在重复计算,故采用标记法(旗鼓相当?)。
class Solution(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0
self.depth = 0
self.dfs(root, 0)
return self.depth
# 深度优先搜索,逐层标记
def dfs(self, root, level):
if not root: return
if self.depth < level + 1:
self.depth = level + 1
self.dfs(root.left, level+1)
self.dfs(root.right, level+1)给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:

输入:root = [3,9,20,null,null,15,7] 输出:2 示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root: return 0
left, right = self.minDepth(root.left), self.minDepth(root.right)
if left and right:
return 1 + min(left, right)
elif left:
return 1 + left
elif right:
return 1 + right
else:
return 1给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
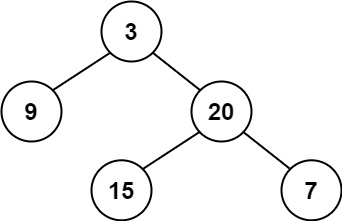
输入:root = [3,9,20,null,null,15,7] 输出:true
上一题的升级版···
前序遍历
root子树平衡 = root的左右深度差不超过1 且 left子树平衡 且 right子树平衡
class Solution(object):
def isBalanced(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root: return True
def depth(root):
if not root: return 0
return max(depth(root.left), depth(root.right))+1
if abs(depth(root.left) - depth(root.right)) >1:
return False
if not self.isBalanced(root.left) or not self.isBalanced(root.right):
return False
return True由于每一次都存在递归,存在重复,所以比较耗时。
后序遍历:
注意到在求根节点深度的过程中其实已经把每一个子节点的深度都求过了,因此我们可以采用后序遍历,先求左右子树的深度,一边计算深度,一边判断是否平衡。
定义helper(root)的含义为:当root为根节点的子树平衡时,helper(root)等于其深度,否则helper(root)=False
# 后序递归,深度优先搜索
class Solution(object):
def isBalanced(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root: return True
def helper(root):
if not root: return 0
left=helper(root.left)
right=helper(root.right)
# 左子树不平衡或者右子树不平衡
if left is False or right is False: return False
# 左右子树都平衡 此时left和right为左右子树的深度 判断root为根节点的子树是否平衡
if abs(left-right)>1: return False
# 左右子树 和root为根节点的当前树 都平衡 返回root为根的树深度
return max(left, right)+1
return True if helper(root) else False给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 : 给定二叉树
1 / \ 2 3 / \ 4 5返回 3, 它的长度是路径 [4->2->1->3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
将二叉树的直径转换为:二叉树的每个节点的左右子树的高度和的最大值。主要还是递归、分治的**。
class Solution(object):
def diameterOfBinaryTree(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0
self.max = 0
self.deep(root)
return self.max
def deep(self, root):
if not root: return 0
left, right = self.deep(root.left), self.deep(root.right) # 获取当前节点的左右分支的高度
if left + right > self.max: # 如果和(左右分支可构成通路)大于当前值,替换
self.max = left + right
return max(left, right) + 1 # 返回当前节点的最大高度
class Solution(object):
def diameterOfBinaryTree(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0
left, right = self.deep(root.left), self.deep(root.right)
return max(max(self.diameterOfBinaryTree(root.left), self.diameterOfBinaryTree(root.right)), left+right)
def deep(self, root):
if not root: return 0
left, right = self.deep(root.left), self.deep(root.right)
return max(left, right) + 1路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:

输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6 示例 2:
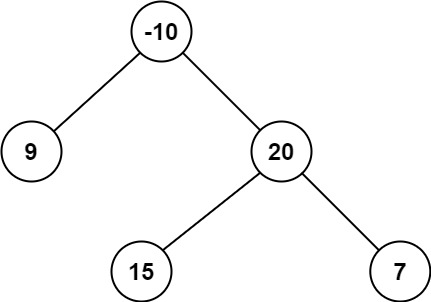
输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
此题是上一题的变种,需要计算当前值。
class Solution(object):
def maxPathSum(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0
self.max = float("-inf")
self.sum(root)
return self.max
def sum(self, root):
if not root: return 0 # 叶子节点的左右支路为0
left = max(0, self.sum(root.left)) # 如果左右分支,小于0,则丢弃
right = max(0, self.sum(root.right))
self.max = max(self.max, left+root.val+right) # 更新最大值
return max(left, right) + root.val # 返回当前节点的所计算的值给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
注意:两个节点之间的路径长度由它们之间的边数表示。
示例 1:
输入:
5 / \ 4 5 / \ \ 1 1 5输出: 2 示例 2:
输入:
1 / \ 4 5 / \ \ 4 4 5输出: 2
同样与上两题类似,但是增加约束条件是值相等,同时表示为边数,而不是长度。
class Solution(object):
def longestUnivaluePath(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0
self.max = 0
self.value(root)
return self.max
def value(self, root):
if not root.left and not root.right: return 0 # 没有左右分支
left = self.value(root.left)+1 if root.left else 0 # 有左分支
right = self.value(root.right)+1 if root.right else 0 # 有右分支
if left != 0 and root.left.val != root.val: # 判断是否值相等,否则为0
left = 0
if right !=0 and root.right.val != root.val:
right = 0
self.max = max(self.max, left + right) # 左右相加,为边数
return max(left, right)class Solution(object):
def longestUnivaluePath(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0
self.max = 0
self.value(root)
return self.max
def value(self, root):
if not root: return 0
left = self.value(root.left)
right = self.value(root.right)
L = R = 0
if root.left and root.left.val == root.val:
L = left + 1
if root.right and root.right.val == root.val:
R = right + 1
self.max = max(self.max, L + R)
return max(L, R) 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 2:
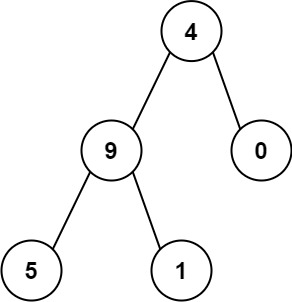
输入:root = [4,9,0,5,1] 输出:1026 解释: 从根到叶子节点路径 4->9->5 代表数字 495 从根到叶子节点路径 4->9->1 代表数字 491 从根到叶子节点路径 4->0 代表数字 40 因此,数字总和 = 495 + 491 + 40 = 1026
主要是深度优先搜索,采用前向搜索:
class Solution(object):
def sumNumbers(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0
self.res = 0
self.dfs(root, 0)
return self.res
def dfs(self, root, tmp):
if not root: return
tmp = 10*tmp + root.val # tmp用于保存到当前的值
if not root.left and not root.right:
self.res += tmp
return
self.dfs(root.left, tmp)
self.dfs(root.right, tmp)给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true
与上一题类似:
class Solution(object):
def hasPathSum(self, root, targetSum):
"""
:type root: TreeNode
:type targetSum: int
:rtype: bool
"""
if not root: return False
self.flag = False
def dfs(root, tmp):
if not root: return
tmp += root.val
if not root.left and not root.right:
if tmp == targetSum:
self.flag = True
return
dfs(root.left, tmp)
dfs(root.right, tmp)
dfs(root, 0)
return self.flag给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
保存所有路径:
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:
if not root: return []
ans = []
def dfs(root, tmp):
if not root: return
if not root.left and not root.right:
tmp += [root.val]
if sum(tmp) == targetSum:
ans.append(tmp)
dfs(root.left, tmp+[root.val])
dfs(root.right, tmp+[root.val])
dfs(root, [])
return ans给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1 /
2 3
5输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
深度优先搜索:
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
if not root: return None
ans = []
def dfs(root, tmp):
tmp += str(root.val)
if not root.left and not root.right:
ans.append(tmp)
return
if root.left: dfs(root.left, tmp+"->")
if root.right: dfs(root.right, tmp+"->")
dfs(root, "")
return ans给定一个二叉搜索树 root 和一个目标结果 k,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
示例 1:

输入: root = [5,3,6,2,4,null,7], k = 9 输出: true
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findTarget(self, root: TreeNode, k: int) -> bool:
dic = dict()
self.flag = False
def dfs(root):
if not root: return
if k - root.val in dic:
self.flag = True
dic[root.val] = 0
dfs(root.left)
dfs(root.right)
dfs(root)
return self.flag给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:

输入:n = 3 输出:5 示例 2:
输入:n = 1 输出:1
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/unique-binary-search-trees 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
假设n个节点存在二叉排序树的个数是G(n),令f(i)为以i为根的二叉搜索树的个数
即有:G(n) = f(1) + f(2) + f(3) + f(4) + ... + f(n)
n为根节点,当i为根节点时,其左子树节点个数为[1, 2, 3,..., i-1],右子树节点个数为[i+1, i+2, ...n],所以当i为根节点时,其左子树节点个数为i-1个,右子树节点为n-i,即f(i) = G(i-1)*G(n-i),
上面两式可得:G(n) = G(0)*G(n-1)+G(1)*(n-2)+...+G(n-1)*G(0)
class Solution:
def numTrees(self, n: int) -> int:
dp = [0] * (n+1)
dp[0] = 1
dp[1] = 1
for i in range(2,n+1):
for j in range(1,i+1):
dp[i] += dp[j-1] * dp[i-j]
return dp[n]给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
示例 1:

输入:n = 3 输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]] 示例 2:
输入:n = 1 输出:[[1]]
class Solution:
def generateTrees(self, n: int) -> List[TreeNode]:
def generate(start, end):
if start > end:
return [None]
tmp = []
for i in range(start, end+1):
left = generate(start, i-1)
right = generate(i+1, end)
for itemleft in left:
for itemright in right:
node = TreeNode(i)
node.left = itemleft
node.right = itemright
tmp.append(node)
return tmp
return generate(1, n)给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
示例 1:
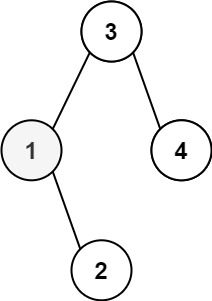
输入:root = [3,1,4,null,2], k = 1 输出:1
示例 2:
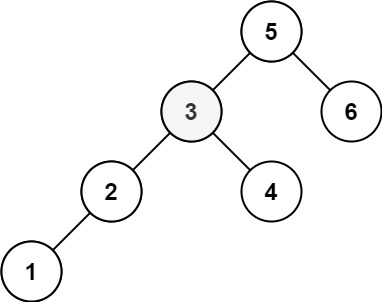
输入:root = [5,3,6,2,4,null,null,1], k = 3 输出:3
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
l = []
def midsearch(root):
if root:
midsearch(root.left)
l.append(root.val)
midsearch(root.right)
midsearch(root)
return l[k - 1]
# 非递归
class Solution:
def kthSmallest(self, root, k):
stack = []
cur = root
while stack or cur:
while cur:
stack.append(cur) # 这里注意一定是append当前遍历的节点,不是left节点
cur = cur.left
cur = stack.pop()
k -= 1
if k == 0:
return cur.val
cur = cur.right给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:

输入:root = [1,2,3,4,5,6] 输出:6
class Solution:
def countNodes(self, root: TreeNode) -> int:
self.cnt = 0
def dfs(node):
if not node: return
self.cnt += 1
dfs(node.left)
dfs(node.right)
dfs(root)
return self.cnt给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1 / \ 2 2 / \ / \ 3 4 4 3但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1 / \ 2 2 \ \ 3 3进阶:
你可以运用递归和迭代两种方法解决这个问题吗?
如果所给根节点,为空,那么是对称。如果不为空的话,当左子树与右子树对称时,则对称。如何判断左右子树对称?如果左树的左孩子与右树的右孩子对称,左树的右孩子与右树的左孩子对称,那么这个左树和右树就对称。
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
def check(node1, node2):
if not node1 and not node2:
return True
elif not node1 or not node2:
return False
if node1.val != node2.val:
return False
return check(node1.left, node2.right) and check(node1.right, node2.left)
return check(root, root)迭代就是层序遍历,然后检查每一层是不是回文数组
class Solution(object):
def isSymmetric(self, root):
queue = [root]
while(queue):
next_queue = list()
layer = list()
for node in queue:
if not node:
layer.append(None)
continue
next_queue.append(node.left)
next_queue.append(node.right)
layer.append(node.val)
if layer != layer[::-1]:
return False
queue = next_queue
return True实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
二分法:
class Solution(object):
def mySqrt(self, x):
"""
:type x: int
:rtype: int
"""
if x==1:
return x
left = 0
right = x
while (right - left) > 1:
middle = int((left+right)/2)
if x/middle < middle:
right = middle
else:
left = middle
return left牛顿迭代法: $$ x_{i+1}=\frac{x_i+\frac{C}{x_i}}{2} $$
class Solution(object):
def mySqrt(self, x):
num = x
while abs(x - num * num) > 0.01:
num = (num + x/num) / 2.0
return int(num)给定一个 正整数 num ,编写一个函数,如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
进阶:不要 使用任何内置的库函数,如 sqrt 。
示例 1:
输入:num = 16 输出:true
与上一题类似:
class Solution(object):
def isPerfectSquare(self, num):
"""
:type num: int
:rtype: bool
"""
if num==1: return True
L, R = 0, num
while (R-L)>1:
mid = (R+L)//2
if num/mid < mid:
R = mid
else:
L = mid
return num==L*L给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a2 + b2 = c 。
示例 1:
输入:c = 5 输出:true 解释:1 * 1 + 2 * 2 = 5
双指针
- i 从 0 开始
- j 从可取的最大数 int(math.sqrt(c)) 开始
- total = i * i + j * j
- total > c: j = j - 1,将 total 值减小
- total < c: i = i + 1,将 total 值增大
- total == c:返回 True
import math
class Solution(object):
def judgeSquareSum(self, c):
"""
:type c: int
:rtype: bool
"""
j = int(math.sqrt(c))
i = 0
while i <= j:
total = i * i + j * j
if total > c:
j = j - 1
elif total < c:
i = i + 1
else:
return True
return False实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。
示例 1:
输入:x = 2.00000, n = 10 输出:1024.00000 示例 2:
输入:x = 2.10000, n = 3 输出:9.26100 示例 3:
输入:x = 2.00000, n = -2 输出:0.25000 解释:2-2 = 1/22 = 1/4 = 0.25
采用递归:
class Solution(object):
def myPow(self, x, n):
"""
:type x: float
:type n: int
:rtype: float
"""
def dfs(x, n):
if n==0: return 1
tmp = dfs(x, n//2)
if n%2==1:
return tmp*tmp*x
else:
return tmp*tmp
if n<0:
x, n = 1.0/x, -n
return dfs(x, n)快速幂:通过对数进行移位操作实现
class Solution(object):
def myPow(self, x, n):
"""
:type x: float
:type n: int
:rtype: float
"""
res = 1
# 小于0时,转变为正数情况
if n < 0: x, n = 1 / x, -n
while n:
# 将n的二进制第一位与1相与,为1,说明是奇数,需要多一步相乘
if n & 1: res *= x
# 偶数,为x的平方
x *= x
n >>= 1 # 右移,减半
return res你的任务是计算 ab 对 1337 取模,a 是一个正整数,b 是一个非常大的正整数且会以数组形式给出。
示例 1:
输入:a = 2, b = [3] 输出:8 示例 2:
输入:a = 2, b = [1,0] 输出:1024 示例 3:
输入:a = 1, b = [4,3,3,8,5,2] 输出:1 示例 4:
#模运算公式
(a + b) % p = (a % p + b % p) % p
(a - b) % p = (a % p - b % p) % p
(a * b) % p = (a % p * b % p) % p
a ^ b % p = ((a % p)^b) % p
# 基于两个重要的性质
a*b % mod = a%mod * b %mod
a^123 % mod = 【a^3 % mod 】* 【(a^12)^10 % mod】
# 逐元素处理class Solution(object):
def superPow(self, a, b):
"""
:type a: int
:type b: List[int]
:rtype: int
"""
ans, base = 1, a%1337
def powf(x, n): # 快速幂
res = 1
while n:
if n & 1: res =res*x%1337
x = (x*x)%1337
n >>= 1
return res
for i in range(len(b)-1, -1, -1): # 从幂的个位开始
ans = ans*powf(base, b[i])%1337 # 分步计算
base = powf(base, 10) # base变化
return ans
# 简化:
class Solution(object):
def superPow(self, a, b):
ans, base = 1, a%1337
while b:
ans = (ans* ((base**b.pop())%1337))%1337
base = (base**10)%1337
return ans已有方法 rand7 可生成 1 到 7 范围内的均匀随机整数,试写一个方法 rand10 生成 1 到 10 范围内的均匀随机整数。
不要使用系统的 Math.random() 方法。
示例 1:
输入: 1 输出: [7] 示例 2:
输入: 2 输出: [8,4] 示例 3:
输入: 3 输出: [8,1,10]
rand7()能等概率生成17; rand7() - 1能等概率生成06; (rand7() - 1) * 7能等概率生成{0, 7, 14, 21, 28, 35, 42}; (rand7() - 1) * 7 + rand7()能等概率生成1~49。
class Solution:
def rand10(self):
"""
:rtype: int
"""
while True:
res = (rand7()-1)*7 + rand7()#构造1~49的均匀分布
if res <= 40:#剔除大于40的值,1-40等概率出现。
break
return res%10+1#构造1-10的均匀分布在无限的整数序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...中找到第 n 位数字。
注意:n 是正数且在 32 位整数范围内(n < 231)。
示例 1:
输入:3 输出:3 示例 2:
输入:11 输出:0 解释:第 11 位数字在序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... 里是 0 ,它是 10 的一部分。
主要分为两部分,首先计算前缀部分,再计算尾部。
- 小于10,直接返回。(step 1)
- 否则,计算前缀部分,全部被占用部分总共有多少位即
length。(step 2) - 计算尾部,其一、计算第一个数字即
pow(10, i-1)。其二、推理出最后一个出现的多位数字即num,并计算出位于第几位即index。(step 3)
'''
1 - [1,9] 9个
2 - [10,99] 90个
3 - [100,999] 900个
4 - [1000,9999] 9000个
.........2^31-1 = 2147483647
'''
class Solution:
def findNthDigit(self, n: int) -> int:
if n < 10: return n
L, N, idx = 0, 9, 1
while L < n:
L += N * idx
N *= 10 # 基数9
idx += 1 # 第几层
N, idx = N//10, idx-1 # 满足条件后跳出,会溢出
L -= N * idx
num = pow(10, idx-1) + (n-L-1)//idx # 计算到达哪个数
index = (n-L-1)%idx # 这个数的第几位
return int(str(num)[index])在自然数1-n之间,任意取两个数x和y,如果x%y=k,则为成功的一对,计算在1-n之间,有多少对满足x%y=k。
例子:n=5,k=2,有4对:(2,3), (2,4),(2,5),(5,3)
此类题不能采用暴力搜索,逐个判断,而是采用生成法,逐个生成。
利用x%y=k,那么x = i*y+k <=n,逐个生成,计算可生成多少个。
nums = [[5,2],[7,3]]
def fun(n, k):
if k > n: return 0
res, y = 0, 1
while y <= n:
i = 0
while True:
if k < y and ( i*y + k <=n):
res +=1 # res.append([i*y + k, y]) 假如输出对
i += 1
else: break
y += 1
return res
for n, k in nums:
print(fun(n,k))给定一个不含重复数字的数组
nums,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
DFS方法:
class Solution:
def permute(self, nums):
ret = []
path = []
def dfs(li):
if len(li) == len(path):
ret.append(path[:])
for i in li:
if i not in path:
path.append(i)
dfs(li)
path.pop()
dfs(nums)
return ret回溯法的三个基本要素:
- 路径:已经做出的选择;
- 选择列表:当前可以做出的选择;
- 结束条件:结束一次回溯算法的条件,即遍历到决策树的叶节点;
回溯法解决问题的通用框架为:
# 回溯算法,复杂度较高,因为回溯算法就是暴力穷举,遍历整颗决策树是不可避免的
结果 = []
def backtrack(路径, 选择列表):
if 满足结束条件:
结果.append(路径)
return
for 选择 in 选择列表: # 核心代码段
做出选择
递归执行backtrack
撤销选择注意:对于回溯算法,不管怎么优化,回溯算法的时间复杂度都不可能低于O(N!),因为回溯算法本质上是穷举,穷举整颗决策树是不可避免的,这也是回溯算法的缺点,复杂度很高。
主要的过程如下图:
class Solution:
def permute(self, nums):
ret = []
path = []
def backtrace(li):
if not li: # 如果li为[],说明没有元素了,则返回保存的所有path,将其加入结果中
return ret.append(path[:])
for i, item in enumerate(li):
path.append(item) # 加入当前的
backtrace(li[:i]+li[i+1:]) # 递归添加列表中除item之外的元素
path.pop() # 撤销加入的item,因为与顺序有关,后面还得加入
backtrace(nums)
return ret给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2], [1,2,1], [2,1,1]]
在上一题的基础上,去掉重复的。
class Solution(object):
def permuteUnique(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
ans, path = [], []
def dfs(num):
if not num and path not in ans:
ans.append(path[:])
for i,it in enumerate(num):
path.append(it)
dfs(num[:i]+num[i+1:])
path.pop()
dfs(nums)
return ans采用集合结构去重,可提升效率.
class Solution(object):
def permuteUnique(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
ans, path = [], []
def dfs(num):
if not num:
ans.append(path[:])
tmp = set()
for i,it in enumerate(num):
if it in tmp: # 集合元素去重
continue
tmp.add(it)
path.append(it)
dfs(num[:i]+num[i+1:])
path.pop()
dfs(nums)
return ans实现获取 下一个排列 的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3] 输出:[1,3,2]
从数组倒着查找,找到nums[i] 比nums[i+1]小的位置,就将nums[i]跟nums[i+1]到nums[nums.length - 1]当中找到一个最小的比nums[i]大的元素交换。交换后,再把nums[i+1]到nums[nums.length-1]排序。
- k,l=0,0
- loop:找到a<b的最大位置, 记录k,l, 并对换ab
- loop:位置k之后的序列反向
- 如果 k==l==0, 也就是说没有找到符合条件的ab:则整个数组反向
class Solution(object):
def nextPermutation(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
N = len(nums)-1
idx = 0
L = 0
for i in range(N, 0, -1):
if nums[i-1]<nums[i]:
idx=i-1
break
for j in range(N, idx, -1):
if nums[j]>nums[idx]:
L=j
break
if idx!=0 or L!=0:
nums[idx], nums[L] = nums[L], nums[idx]
p = nums[idx+1:]
nums[idx+1:] = p[::-1]
else:
nums[:] = nums[::-1]
return numsclass Solution(object):
def nextPermutation(self, nums):
n, index, minindex =len(nums), n-1, -1 #-1是初始最小下标,因为不可能取到负的位置
while index > 0 and nums[index] <= nums[index-1]: #找出第一个升序的位置
index -= 1
if index == 0: #整个数组为降序,直接翻转数组即可
nums[::-1]
else: #否则在nums[index:]中找出比nums[index-1]第一大的元素;
for i in range(index,n):
if nums[i] > nums[index-1]:
if minindex == -1 or nums[minindex]>nums[i]:
minindex = i
nums[index-1], nums[minindex] = nums[minindex], nums[index-1] #找出后,交换两人的位置再进行排序即可
nums[index:] = sorted(nums[index:])
return nums给你一个正整数 n ,请你找出符合条件的最小整数,其由重新排列 n 中存在的每位数字组成,并且其值大于 n 。如果不存在这样的正整数,则返回 -1 。
注意 ,返回的整数应当是一个 32 位整数 ,如果存在满足题意的答案,但不是 32 位整数 ,同样返回 -1 。
示例 1:
输入:n = 12 输出:21 示例 2:
输入:n = 21 输出:-1
如上一题,将整数划分为数组。
class Solution:
def nextGreaterElement(self, number):
nums = list(map(int, list(str(number))))
n, index, minindex =len(nums), len(nums)-1, -1 #-1是初始最小下标,因为不可能取到负的位置
while index > 0 and nums[index] <= nums[index-1]: #找出第一个升序的位置
index -= 1
if index != 0: # index==0, 整个数组为降序
#否则在nums[index:]中找出比nums[index-1]第一大的元素;
for i in range(index,n):
if nums[i] > nums[index-1]:
if minindex == -1 or nums[minindex]>nums[i]:
minindex = i
nums[index-1], nums[minindex] = nums[minindex], nums[index-1] #找出后,交换两人的位置再进行排序即可
nums[index:] = sorted(nums[index:])
str_ = ''.join(map(str, nums))
if -2**31<= int(str_) <= 2**31-1 and index:
return int(str_)
else: return -1给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。 解集不能包含重复的组合。 示例 1:
输入:candidates = [2,3,6,7], target = 7, 所求解集为: [ [7], [2,2,3] ]
class Solution(object):
def combinationSum(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
candidates.sort()
n, res = len(candidates), []
def dfs(i, tmp_sum, tmp):
for j in range(i, n):
if tmp_sum + candidates[j] > target:
break
if tmp_sum + candidates[j] == target:
res.append(tmp+[candidates[j]])
break
dfs(j, tmp_sum + candidates[j], tmp+[candidates[j]])
dfs(0, 0, [])
return res给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
采用DFS进行
- 首先建立DFS函数,有两个参数,一个是从0开始一直加到n的整数,一个是暂存的列表。
- 先用一个if语句判断回溯结束条件,就是列表的长度是否等于k,如果是的话就添加进res中,然后结束递归函数。
- 如果列表长度小于k的话,就进入循环,将j增大1,且暂存列表加入数字j。
- 全部结束完输出结果ans即可。
class Solution(object):
def combine(self, n, k):
ans = []
def dfs(i, num):
if len(num) == k:
ans.append(num)
return
for j in range(i+1, n+1):
dfs(j, num+[j])
dfs(0, [])
return ansclass Solution(object):
def combine(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
nums = [i for i in range(1,n+1)]
# 明显用回溯法:
res, path = [], []
def dfs(num,i):
if len(path)==k:
res.append(path[:]) # 浅拷贝,这一步很重要
return
for j in range(i,n):
path.append(nums[j]) #
dfs(num[i:],j+1)
path.pop()
# 特殊情况处理
if n==0 or k==0:
return res
dfs(nums,0)
return res给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
class Solution(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
path, ans, n = [], [], len(nums)
def dfs(nums, index):
ans.append(path[:])
for i in range(index, n):
path.append(nums[i])
dfs(nums, i+1) # 递归
path.pop() # 回溯
dfs(nums, 0)
return ans每轮都传递一个数组起始指针的值,保证遍历顺序:
-
第一轮:先遍历以1 开头的所有子集,1→12→123 →13
-
第二轮:遍历以2开头的所有子集,2→23
-
第三轮:遍历以3开头的所有子集,3
-
这样三轮遍历保证能找到全部1开头,2开头,3开头的所有子集;同时,每轮遍历后又把上轮的头元素去掉,这样不会出现重复子集。(包括空集)
class Solution(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
def dfs(nums, index, path, res):
res.append(path) # 添加路径
for i in range(index, len(nums)): # 逐个取单个元素
dfs(nums, i+1, path+[nums[i]], res) # path+[nums[i]]实现了元素的组合,并且从左往右依次取,不重复
res = []
dfs(nums, 0, [], res)
return resclass Solution(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
ans = []
def dfs(start, path):
if start == len(nums):
ans.append(path[:])
else:
dfs(start + 1, path) # 不选
path.append(nums[start])
dfs(start + 1, path) # 选
path.pop()
dfs(0, [])
return ans给你一个整数数组
nums,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
添加去重:
class Solution(object):
def subsetsWithDup(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
nums= sorted(nums)
ans = []
def dfs(start, path):
if start == len(nums):
if not path in ans:
ans.append(path[:])
else:
dfs(start + 1, path) # 不选
path.append(nums[start])
dfs(start + 1, path) # 选
path.pop()
dfs(0, [])
return ans 提高效率:
class Solution:
def subsetsWithDup(self, nums):
# 去重需要排序, 用来存放符合条件结果, 存放符合条件结果的集合
nums, path, ans, n = sorted(nums), [], [], len(nums)
def dfs(nums, index):
ans.append(path[:])
for i in range(index, n):
if nums[i]==nums[i-1] and i >index:
continue
path.append(nums[i])
dfs(nums, i+1) # 递归
path.pop() # 回溯
dfs(nums, 0)
return ans累加数是一个字符串,组成它的数字可以形成累加序列。
一个有效的累加序列必须至少包含 3 个数。除了最开始的两个数以外,字符串中的其他数都等于它之前两个数相加的和。
给定一个只包含数字 '0'-'9' 的字符串,编写一个算法来判断给定输入是否是累加数。
说明: 累加序列里的数不会以 0 开头,所以不会出现 1, 2, 03 或者 1, 02, 3 的情况。
示例 1:
输入: "112358" 输出: true 解释: 累加序列为: 1, 1, 2, 3, 5, 8 。1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
回溯加剪枝:
- 确认边界,当数组长度小于3,则说明无法组合成三个数,返回错误
- 回溯遍历,每次递归的参数有选中剩余的num数组,已符合要求的数字个数(主要为了判断是否有两个数字),前一个数和前第二个数
- 如果当前数字个数小于等于2且剩余数组为空,凑不够三个数则返回false
- 如果剩余数组为空说明所有数字已用完,返回True
- 循环剩余数组
- 剪枝部分:单个的0可以作为一个数,而01,02之类的不能,直接返回
- 剪枝部分:当res已经为True时,可以不用继续回溯了,直接返回
- 循环递归:当数字个数大于等于2时,则判断是否等于前两个数之和,如果是则继续递归,如果不是则直接返回
- 当数字个数不大于2时,则直接递归下一层
class Solution:
def isAdditiveNumber(self, num):
# 回溯法DFS
if len(num)<3:return False
self.res = False
def dfs(res_num, cur_count, first, second):
# res_num:剩余的num数组
# cur_count:当前已选过的num个数
# first、second:前两个数
if cur_count<=2 and not res_num:return # 因为至少要三个数才能做判断
if not res_num:
self.res =True
return
for i in range(len(res_num)):
# 剪枝--单个的0可以作为一个数,而01,02之类的不能,直接返回
if len(res_num[:i+1])!=len(str(int(res_num[:i+1]))):
return
if cur_count>=2:
if int(res_num[:i+1])==first+second:
dfs(res_num[i+1:], cur_count+1, second, int(res_num[:i+1]))
else:
dfs(res_num[i+1:], cur_count+1, second, int(res_num[:i+1]))
if self.res: # 剪枝--当res已经为True时,可以不用继续回溯了,直接返回
return
dfs(num,0,0,0)
return self.res首先遍历前两个数,确定之后判断后面的是不是累加的就可以了。
class Solution:
def isAdditiveNumber(self, num):
n = len(num)
if n < 3:
return False
def check(p1, p2, j):
while j < n:
p = str(int(p1) + int(p2))
if num[j: j+len(p)] != p:
return False
j += len(p)
p1, p2 = p2, p
return True
for i in range(1, n//2+1) if num[0] != "0" else [1]: # 第一个数,逐长度判断
for j in range(i+1, n) if num[i] != "0" else [i+1]: # 第二个数,也逐长度判断
p1 = num[:i]
p2 = num[i:j]
if check(p1, p2, j):
return True
return False给定一个数字字符串 S,比如 S = "123456579",我们可以将它分成斐波那契式的序列 [123, 456, 579]。
形式上,斐波那契式序列是一个非负整数列表 F,且满足:
0 <= F[i] <= 2^31 - 1,(也就是说,每个整数都符合 32 位有符号整数类型); F.length >= 3; 对于所有的0 <= i < F.length - 2,都有 F[i] + F[i+1] = F[i+2] 成立。 另外,请注意,将字符串拆分成小块时,每个块的数字一定不要以零开头,除非这个块是数字 0 本身。
返回从 S 拆分出来的任意一组斐波那契式的序列块,如果不能拆分则返回 []。
示例 1:
输入:"123456579" 输出:[123,456,579] 示例 2:
输入: "11235813" 输出: [1,1,2,3,5,8,13]
模板,再多带个f(n) + f(n+1) == f(n+2)的判断条件
class Solution:
def splitIntoFibonacci(self, S):
def backtrack(cur, temp_state):
if len(temp_state) >= 3 and cur == n: # 退出条件
self.res = temp_state
return
if cur == n: # 剪枝
return
for i in range(cur, n):
if S[cur] == "0" and i > cur: # 当数字以0开头时,应该跳过
return
if int(S[cur: i+1]) > 2 ** 31 - 1 or int(S[cur: i+1]) < 0: # 剪枝
continue
if len(temp_state) < 2:
backtrack(i+1, temp_state + [int(S[cur: i+1])])
else:
if int(S[cur: i+1]) == temp_state[-1] + temp_state[-2]:
backtrack(i+1, temp_state + [int(S[cur: i+1])])
n = len(S)
self.res = []
backtrack(0, [])
return self.res编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"] 输出:"fl" 示例 2:
输入:strs = ["dog","racecar","car"] 输出:"" 解释:输入不存在公共前缀。
思路 1: Python 特性,取每一个单词的同一位置的字母,看是否相同。
class Solution:
def longestCommonPrefix(self, strs):
"""
:type strs: List[str]
:rtype: str
"""
res = ""
for tmp in zip(*strs):
tmp_set = set(tmp)
if len(tmp_set) == 1:
res += tmp[0]
else:
break
return res思路 2:
取一个单词 s,和后面单词比较,看 s 与每个单词相同的最长前缀是多少!遍历所有单词。
class Solution:
def longestCommonPrefix(self, s: List[str]) -> str:
if not s:
return ""
res = s[0]
i = 1
while i < len(s):
while s[i].find(res) != 0:
res = res[0:len(res)-1]
i += 1
return res给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
可以推断出以下要点:
- 有效括号字符串的长度,一定是偶数!
- 右括号前面,必须是相对应的左括号,才能抵消!
- 右括号前面,不是对应的左括号,那么该字符串,一定不是有效的括号!
思考过程是栈的实现过程。因此我们考虑使用栈,当遇到匹配的最小括号对时,我们将这对括号从栈中删除(即出栈),如果最后栈为空,那么它是有效的括号,反之不是。
# 堆栈过程
class Solution:
def isValid(self, s):
dic = {')':'(', ']':'[', '}':'{'} # 根据右侧进行索引、判断
stack = []
for i in s:
if stack and i in dic:
if stack[-1]==dic[i]:
stack.pop()
else:
return False
else:
stack.append(i)
return not stack
# 简化过程
class Solution:
def isValid(self, s):
while '{}' in s or '()' in s or '[]' in s: # 逐步替换,直到为空
s = s.replace('{}', '')
s = s.replace('[]', '')
s = s.replace('()', '')
return s == ''给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()" 输出:2 解释:最长有效括号子串是 "()" 示例 2:
输入:s = ")()())" 输出:4 解释:最长有效括号子串是 "()()" 示例 3:
输入:s = "" 输出:0
不同于上题,为连续括号。
class Solution:
def longestValidParentheses(self, s: str) -> int:
stack, res = [-1], 0
for i, c in enumerate(s):
if c == "(":
stack.append(i)
else:
stack.pop()
if not stack:
stack.append(i)
else:
res = max(res, i - stack[-1])
return res数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"] 示例 2:
输入:n = 1 输出:["()"]
深度优先搜索+回溯,类似于排列组合问题:
class Solution(object):
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
res = []
def dfs(path, lnum, rnum):
if len(path) == 2*n:
res.append(path)
return
if lnum < n:
dfs(path+'(', lnum+1, rnum)
if rnum < lnum:
dfs(path+')', lnum, rnum+1)
dfs('', 0, 0)
return res给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 3:
输入:s = "2[abc]3[cd]ef" 输出:"abcabccdcdcdef"
栈:先进后出,依次遍历完成整个字符串
class Solution(object):
def decodeString(self, s):
stack, num, ans = [], 0, ''
for c in s:
if c.isdigit(): # 计算值
num = num*10 + int(c)
elif c == '[': # 标志位,保存新的字符串
stack.append((ans, num))
num, ans = 0, ''
elif c == ']': # 结束位,对[]之间的值计算
pre, n = stack.pop()
ans = pre + ans * n
else:
ans += c
return ans请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
读入字符串并丢弃无用的前导空格 检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。 读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。 将前面步骤读入的这些数字转换为整数(即,"123" -> 123, "0032" -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。 如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。 返回整数作为最终结果。 注意:
本题中的空白字符只包括空格字符 ' ' 。 除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
示例 1:
输入:s = "42" 输出:42 解释:加粗的字符串为已经读入的字符,插入符号是当前读取的字符。 第 1 步:"42"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"42"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"42"(读入 "42") ^ 解析得到整数 42 。 由于 "42" 在范围 [-231, 231 - 1] 内,最终结果为 42 。 示例 2:
输入:s = " -42" 输出:-42 解释: 第 1 步:" -42"(读入前导空格,但忽视掉) ^ 第 2 步:" -42"(读入 '-' 字符,所以结果应该是负数) ^ 第 3 步:" -42"(读入 "42") ^ 解析得到整数 -42 。 由于 "-42" 在范围 [-231, 231 - 1] 内,最终结果为 -42 。 示例 3:
输入:s = "4193 with words" 输出:4193 解释: 第 1 步:"4193 with words"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"4193 with words"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"4193 with words"(读入 "4193";由于下一个字符不是一个数字,所以读入停止) ^ 解析得到整数 4193 。 由于 "4193" 在范围 [-231, 231 - 1] 内,最终结果为 4193 。 示例 4:
输入:s = "words and 987" 输出:0 解释: 第 1 步:"words and 987"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"words and 987"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"words and 987"(由于当前字符 'w' 不是一个数字,所以读入停止) ^ 解析得到整数 0 ,因为没有读入任何数字。 由于 0 在范围 [-231, 231 - 1] 内,最终结果为 0 。 示例 5:
输入:s = "-91283472332" 输出:-2147483648 解释: 第 1 步:"-91283472332"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"-91283472332"(读入 '-' 字符,所以结果应该是负数) ^ 第 3 步:"-91283472332"(读入 "91283472332") ^ 解析得到整数 -91283472332 。 由于 -91283472332 小于范围 [-231, 231 - 1] 的下界,最终结果被截断为 -231 = -2147483648 。
直接按照示例写程序,同时利用上一题的思路。
class Solution(object):
def myAtoi(self, s):
if not s: return 0
while s[0] == ' ': # 去掉空格
s = s[1:]
if not s: return 0
num, flag = 0, 0
if s[0] == '-' or s[0] == '+': # 判断正负号
flag = 0 if s[0] == '+' else 1
s = s[1:]
elif not s[0].isdigit():
return 0
for c in s: # 获取数值
if c.isdigit(): # 计算值
num = num*10 + int(c)
else:
break
# 范围限制
ans = -num if flag else num
if -2**31 <= ans <= 2**31 - 1:
return ans
else:
return -2**31 if flag else 2**31 - 1给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
示例 1:
输入:s = "1 + 1" 输出:2 示例 2:
输入:s = " 2-1 + 2 " 输出:3 示例 3:
输入:s = "(1+(4+5+2)-3)+(6+8)" 输出:23
class Solution(object):
def calculate(self, s):
s = s.strip()
stack, num, ans, sign = [], 0, 0, 1
for c in s:
if c.isdigit(): # 计算值
num = num*10 + int(c)
elif c == '+' or c == '-':
ans += sign*num
num = 0
sign = 1 if c=='+' else -1
elif c == '(': # 标志位,保存新的字符串
stack.append((ans, sign))
ans, sign = 0, 1
elif c == ')': # 结束位,对[]之间的值计算
ans += sign*num
pre, sign_tmp = stack.pop()
ans = pre + sign_tmp * ans
num = 0
ans += sign*num
return ans给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
示例 1:
输入:s = "3+2*2" 输出:7 示例 2:
输入:s = " 3/2 " 输出:1 示例 3:
输入:s = " 3+5 / 2 " 输出:5
class Solution(object):
def calculate(self, s):
"""
:type s: str
:rtype: int
"""
s = s.strip()
n = len(s)
# sign是上一次的计算符号
stack, num, sign= [], 0, '+'
for i in range(n):
c = s[i]
if c.isdigit(): # 计算值
num = num*10 + int(c)
if c in {'+', '-', '*', '/'} or i == (n-1):
if sign == '+':
stack.append(num)
if sign == '-':
stack.append(-num)
if sign == '*':
stack.append(stack.pop()*num)
if sign == '/':
stack.append(int(stack.pop()/num))
num, sign = 0, c
return sum(stack)根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9 示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
- 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
- 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中。
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
f1 = lambda a,b:a+b
f2 = lambda a,b:a-b
f3 = lambda a,b:a*b
f4 = lambda a,b:int(a/b)
maps = {'+':f1, '-':f2, '*':f3, '/':f4}
stack = []
for i in tokens:
if i in maps:
a = stack.pop()
b = stack.pop()
stack.append(maps[i](b,a))
else:
i = int(i)
stack.append(i)
return stack[-1]给你一个字符串 s ,逐个翻转字符串中的所有 单词 。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
请你返回一个翻转 s 中单词顺序并用单个空格相连的字符串。
说明:
输入字符串 s 可以在前面、后面或者单词间包含多余的空格。 翻转后单词间应当仅用一个空格分隔。 翻转后的字符串中不应包含额外的空格。
示例 1:
输入:s = "the sky is blue" 输出:"blue is sky the" 示例 2:
输入:s = " hello world " 输出:"world hello" 解释:输入字符串可以在前面或者后面包含多余的空格,但是翻转后的字符不能包括。
class Solution:
def reverseWords(self, s: str) -> str:
return ' '.join(s.split()[::-1])给定一个包含大写字母和小写字母的字符串,找到通过这些字母构造成的最长的回文串。
在构造过程中,请注意区分大小写。比如 "Aa" 不能当做一个回文字符串。
注意: 假设字符串的长度不会超过 1010。
示例 1:
输入: "abccccdd"
输出: 7
解释: 我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。
class Solution(object):
def longestPalindrome(self, s):
dic, ans = {}, 0
for ch in s:
if ch not in dic:
dic[ch] = 1
else:
dic[ch] += 1
if dic[ch] == 2:
ans += 2
dic[ch] = 0
return ans if ans == len(s) else ans + 1 # 长度不等,说明是奇数个,放中间,加1定一个非负整数,你至多可以交换一次数字中的任意两位。返回你能得到的最大值。
示例 1 :
输入: 2736 输出: 7236 解释: 交换数字2和数字7。 示例 2 :
输入: 9973 输出: 9973 解释: 不需要交换。
将数字转换为字符,再进行操作
class Solution:
def maximumSwap(self, num):
nums = [int(x) for x in str(num)] # 转化为单个字符
num_sorted = sorted(nums, reverse=True) # 进行排序,从大到小
value = -1
for i in range(len(nums)):
if nums[i] != num_sorted[i]: # 如果排序后的列表与原来不一致,则说明替换了,找到第一个不同的位置
value = num_sorted[i]
index = i
break
if value == -1: # 如果没有,不需要排序,返回即可
return num
else:
for j in range(len(nums)-1, -1, -1): # 反向找到替换的值,并进行交换
if nums[j] == value:
nums[j], nums[index] = nums[index], nums[j]
break
return int(''.join(str(it) for it in nums)) # 将字符串变回整数class Solution:
def maximumSwap(self, num):
nlist = [n for n in str(num)]
num_len = len(nlist)
m = max(nlist)
for i, c in enumerate(nlist):
m = i
for j in range(i+1, num_len):
if nlist[j] >= nlist[m]:
# 注意相等情况, 取最后一个位置, 保证 1993 => 9913, 而不是 9193 ;
m = j
if m != i and nlist[i] != nlist[m]:
# 注意此处找到的最大值和当前位置相等, 则不交换!!!, 比如 98368 => 98863
nlist[i], nlist[m] = nlist[m], nlist[i]
break
return int("".join(nlist))class Solution(object):
def maximumSwap(self, num):
if num <= 10:
return num
# 首位数最大,则不需要移动首位数
# 首位数不是最大,与最后一个最大数交换位置
def helper(num_list):
if not num_list:
return []
max_n = max(num_list)
if max_n == num_list[0]:
return [max_n] + helper(num_list[1:])
i = 0
for idx, n in enumerate(num_list):
if max_n == n:
i = idx
num_list[0], num_list[i] = num_list[i], num_list[0]
return num_list
return int(''.join(helper(list(str(num)))))按字典 wordList 完成从单词 beginWord 到单词 endWord 转化,一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> ... -> sk 这样的单词序列,并满足:
每对相邻的单词之间仅有单个字母不同。 转换过程中的每个单词 si(1 <= i <= k)必须是字典 wordList 中的单词。注意,beginWord 不必是字典 wordList 中的单词。 sk == endWord 给你两个单词 beginWord 和 endWord ,以及一个字典 wordList 。请你找出并返回所有从 beginWord 到 endWord 的 最短转换序列 ,如果不存在这样的转换序列,返回一个空列表。每个序列都应该以单词列表 [beginWord, s1, s2, ..., sk] 的形式返回。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"] 输出:[["hit","hot","dot","dog","cog"],["hit","hot","lot","log","cog"]] 解释:存在 2 种最短的转换序列: "hit" -> "hot" -> "dot" -> "dog" -> "cog" "hit" -> "hot" -> "lot" -> "log" -> "cog" 示例 2:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"] 输出:[] 解释:endWord "cog" 不在字典 wordList 中,所以不存在符合要求的转换序列。
要求最短路径,自然考虑用BFS。
class Solution:
def findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:
words = set(wordList)
if endWord not in words: return []
dic = collections.defaultdict(list)
n = len(wordList[0])
for w in words:
for i in range(n):
dic[w[:i] + '*' + w[i+1:]].append(w)
q, s = [(beginWord, [beginWord])], []
res = []
seen = set()
while q:
while q:
w, path = q.pop()
seen.add(w)
if w == endWord: res.append(path)
for i in range(n):
for nxt in dic[w[:i] + '*' + w[i+1:]]:
if nxt not in seen:
s.append((nxt, path + [nxt]))
if res: return res
q, s = s, q
return []获取多行文本(均为英文符),每行文本中有若干英文逗号将该行文本分隔成多个单元。因此,多行文本可以用一个表格来描述,例如输入: aa,bb,ce dddd, ee 期望的输入如下:
+----+--+--+ | aa|bb|cc| +----+--+--+ |dddd|ee| | +----+--+--+
湖足的规则如下: (1)表格每一行和每一列中间有分隔符:+表示交叉符,"表示棍向边框符,T表示纵向边框符。
(2)每一列的宽度等于该列最长的文本,如果单元格内文本长度小于宽度,则在左侧补齐空格。
(3)列的数量等于列最多的一行包含的列数量。
(4)文本行中每一个逗号都需要进行分割,逗号前后如果出现了空格需要忽略。如输入为:
str_lit = []
while True:
try:
tmp = input().split(',')
#tmp = [it.strip() for it in tmp]
str_lit.append(tmp)
except:
break
str_lit = [[it.strip() for it in item] for item in str_lit]
m = len(str_lit)
num_matrix = [[len(i) for i in it] for it in str_lit]
n = max([len(it) for it in num_matrix])
num_list = [0]*n
for it in num_matrix:
for i, key in enumerate(it):
if key > num_list[i]:
num_list[i] = key
str_ = ['-'*it for it in num_list]
str_tmp = '+' + '+'.join(str_) + '+'
print(str_tmp)
for it in str_lit:
str_line = '|'
for i, key in enumerate(it):
if len(key) < num_list[i]:
str_line += ' ' * (num_list[i] - len(key))+ key
else:
str_line += key
str_line += '|'
if i < n:
for j in range(i+1, n):
str_line += ' ' * num_list[i]
str_line += '|'
print(str_line)
print(str_tmp)二分查找的复杂度为O(log2n)
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4 示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2 输出: -1 解释: 2 不存在 nums 中因此返回 -1
1.为什么 while 循环的条件中是 <=,而不是 <?
答:因为初始化 right 的赋值是 nums.length - 1,即最后一个元素的索引,而不是 nums.length。
这二者可能出现在不同功能的二分查找中,区别是:前者相当于两端都闭区间 [left, right],后者相当于左闭右开区间 [left, right),因为索引大小为 nums.length 是越界的。
这个算法中使用的是前者 [left, right] 两端都闭的区间。这个区间其实就是每次进行搜索的区间。
什么时候应该停止搜索呢?当然,找到了目标值的时候可以终止:
if(nums[mid] == target)
return mid;
但如果没找到,就需要 while 循环终止,然后返回 -1。那 while 循环什么时候应该终止?搜索区间为空的时候应该终止,意味着你没得找了,就等于没找到嘛。
while(left <= right) 的终止条件是 left == right + 1,写成区间的形式就是 [right + 1, right],或者带个具体的数字进去 [3, 2],可见这时候区间为空,因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的,直接返回 -1 即可。
while(left < right) 的终止条件是 left == right,写成区间的形式就是 [left, right],或者带个具体的数字进去 [2, 2],这时候区间非空,还有一个数 2,但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了,索引 2 没有被搜索,如果这时候直接返回 -1 就是错误的。
当然,如果你非要用 while(left < right) 也可以,我们已经知道了出错的原因,就打个补丁好了:
//...
while(left < right) {
// ...
}
return nums[left] == target ? left : -1;
2、为什么 left = mid + 1,right = mid - 1?我看有的代码是 right = mid 或者 left = mid,没有这些加加减减,到底怎么回事,怎么判断?
答:这也是二分查找的一个难点,不过只要你能理解前面的内容,就能够很容易判断。
刚才明确了「搜索区间」这个概念,而且本算法的搜索区间是两端都闭的,即 [left, right]。那么当我们发现索引 mid 不是要找的 target 时,下一步应该去搜索哪里呢?
当然是去搜索 [left, mid-1] 或者 [mid+1, right] 对不对?因为 mid 已经搜索过,应该从搜索区间中去除。
class Solution:
def search(self, nums: List[int], target: int) -> int:
L, R = 0, len(nums)-1
while L <= R:
mid = (L+R)//2
if nums[mid] > target:
R = mid -1
elif nums[mid] < target:
L = mid + 1
else:
return mid
return -1
# [left, right)
class Solution:
def search(self, nums: List[int], target: int) -> int:
L, R = 0, len(nums)
while L < R:
mid = (L+R)//2
if nums[mid] > target:
R = mid
elif nums[mid] < target:
L = mid + 1
else:
return mid
return -1给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5 输出: 2 示例 2:
输入: nums = [1,3,5,6], target = 2 输出: 1 示例 3:
输入: nums = [1,3,5,6], target = 7 输出: 4
如上一题,未找到时,返回左侧查找值:
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
L, R = 0, len(nums)-1
while L <= R:
mid = (L+R)//2
if nums[mid] > target:
R = mid -1
elif nums[mid] < target:
L = mid + 1
else:
return mid
return L给定一个只包含整数的有序数组,每个元素都会出现两次,唯有一个数只会出现一次,找出这个数。
示例 1:
输入: nums = [1,1,2,3,3,4,4,8,8] 输出: 2 示例 2:
输入: nums = [3,3,7,7,10,11,11] 输出: 10
class Solution:
def singleNonDuplicate(self, nums: List[int]) -> int:
L, R = 0, len(nums)-1
while L < R:
mid = (L+R)//2
if mid & 1:
if nums[mid] == nums[mid-1]:
L = mid + 1
else:
R = mid -1
else:
if nums[mid] == nums[mid+1]:
L = mid + 1
else:
R = mid
return nums[L]整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
进阶:一个时间复杂度为 O(log n)
# 偷懒法
class Solution(object):
def search(self, nums, target):
if target not in nums:
return -1
else:
return nums.index(target)采用二分法(有序数组)
-
判断 mid 与 left 对应元素的大小关系,从而判断哪边是有序的:选取 left(选 right 也可以),如果
nums[mid] > nums[left],则左边有序;反之右边有序。 -
判断 mid 对应元素与 target 的大小关系。
class Solution(object):
def search(self, nums, target):
if not nums:
return -1
left = 0
right = len(nums)-1
while left <=right:
mid = (left+right)//2
if nums[mid] == target:
return mid
if nums[left] <= nums[mid]:
if nums[left] <= target <= nums[mid]:
right = mid - 1
else:
left = mid + 1
if nums[mid] <= nums[right]:
if nums[mid] <= target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -1已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
给你 旋转后 的数组 nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。
示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0 输出:true 示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3 输出:false
与上一题的区别在于,这题的数组中可能会出现重复元素。二分查找的本质就是在循环的每一步中考虑排除掉哪些元素,本题在用二分查找时,只有在nums[mid]严格大于或小于左边界时才能判断它左边或右边是升序的,这时可以再根据nums[mid], target与左右边界的大小关系排除掉一半的元素;当nums[mid]等于左边界时,无法判断是mid的左边还是右边是升序数组,而只能肯定左边界不等于target(因为nums[mid] != target),所以只能排除掉这一个元素,让左边界加一。
class Solution(object):
def search(self, nums, target):
if not nums: return False
L, R = 0, len(nums)-1
while L <= R:
mid = (L+R)//2
if nums[mid] == target:
return True
elif nums[L] < nums[mid]:
if nums[L] <= target < nums[mid]:
R = mid -1
else:
L = mid + 1
elif nums[mid] < nums[L]:
if nums[mid] < target <= nums[R]:
L = mid + 1
else:
R = mid - 1
elif nums[L]==nums[mid]:
L += 1
return False搜索旋转数组。给定一个排序后的数组,包含n个整数,但这个数组已被旋转过很多次了,次数不详。请编写代码找出数组中的某个元素,假设数组元素原先是按升序排列的。若有多个相同元素,返回索引值最小的一个。
示例1:
输入: arr = [15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14], target = 5 输出: 8(元素5在该数组中的索引) 示例2:
输入:arr = [15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14], target = 11 输出:-1 (没有找到)
重复时:[5,5,5,1,2,3,4,5] ,5
假如出现重复数字时:
class Solution(object):
def search(self, nums, target):
if not nums: return False
L, R = 0, len(nums)-1
while(nums[0] == nums[R]): R-=1 # 去掉右侧重复
while L <= R:
mid = (L+R)//2
if nums[mid] == target:
while nums[mid] == nums[mid-1] and mid > 0:
mid -=1
return mid
elif nums[L] < nums[mid]:
if nums[L] <= target < nums[mid]:
R = mid -1
else:
L = mid + 1
elif nums[mid] < nums[L]:
if nums[mid] < target <= nums[R]:
L = mid + 1
else:
R = mid - 1
elif nums[L]==nums[mid]:
L += 1
return -1已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2] 若旋转 7 次,则可以得到 [0,1,2,4,5,6,7] 注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
示例 1:
输入:nums = [3,4,5,1,2] 输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
class Solution(object):
def findMin(self, nums):
if not nums: return None
L, R = 0, len(nums) - 1
while L < R:
mid = (L + R) // 2
if nums[mid] < nums[R]: # mid可能为最小值
R = mid
else: # mid肯定不是最小值
L = mid + 1
return nums[L]已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,4] 若旋转 7 次,则可以得到 [0,1,4,4,5,6,7] 注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个可能存在 重复 元素值的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
示例 1:
输入:nums = [1,3,5] 输出:1 示例 2:
输入:nums = [2,2,2,0,1] 输出:0
接上一题,去除重复:
class Solution:
def findMin(self, nums: List[int]) -> int:
if not nums: return None
L, R = 0, len(nums) - 1
while L < R:
mid = (L + R) // 2
if nums[mid] < nums[R]: # mid可能为最小值
R = mid
elif nums[mid] > nums[R]: # mid肯定不是最小值
L = mid + 1
else:
R -=1
return nums[L]先去除首尾相同的元素,后再找旋转点,确定位置后,再分类确定最小值位置:
class Solution:
def findMin(self, nums: List[int]) -> int:
if not nums: return None
L, R = 0, len(nums)-1
while(nums[0] == nums[R]): # 删除重复值
R-=1
if R < 0: return nums[0]
nums.pop()
# 确定旋转点
while L < R:
mid = (L+R+1)//2
if nums[mid]>=nums[0]:
L = mid
else:
R = mid -1
# 判断各情况,确定最小值位置
if L == 0:
if nums[L] >nums[L+1]: # 可能第一个为最大值,但下一个为最小值
return nums[L+1]
else:
return nums[-1] # 也可能是下降序列
elif L == (len(nums)-1): # 上升序列
return nums[0]
else:
return nums[L+1] # 正常旋转给定一个旋转数组,找出其中位数值
如:[4,8,9,11,1,2,3],输出4
[8,7,4,2],输出7或4
先找出旋转数组的旋转点,在计算中位数在第几个:
class Solution:
def findMin(self, nums):
if not nums: return None
L, R = 0, len(nums)-1
while L < R:
mid = (L+R+1)//2
# 由于第一段满足 >=nums[0],第二段不满足 >=nums[0],当使用 >=nums[0] 进行二分,二分出的是满足此性质的最后一个数
if nums[mid]>=nums[0]:
L = mid
else:
R = mid -1
# 当L为首尾时,为完整的下降或上升序列;当旋转点idx大于一般时,在前半部分
if L == 0 or L == (len(nums)-1) or L > len(nums)//2:
return nums[len(nums)//2]
# 否则在后半部分
else:
return nums[L - len(nums)//2]
s = Solution()
print(s.findMin([4,8,9,11,1,2,3]))
print(s.findMin([3,4,8]))
print(s.findMin([8,7,4,2])) 美团8.24面试题-查找数组最大值/852-山脉数组的峰顶索引
符合下列属性的数组 arr 称为 山脉数组 : arr.length >= 3 存在 i(0 < i < arr.length - 1)使得: arr[0] < arr[1] < ... arr[i-1] < arr[i] arr[i] > arr[i+1] > ... > arr[arr.length - 1] 给你由整数组成的山脉数组 arr ,返回任何满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。
示例 1:
输入:arr = [0,1,0] 输出:1
例如:数组[1,5,6,7,9,5,2],返回下标4
数组的规律是,最大值像座山峰,左侧是数值递增,右侧递减,那么:
- nums[mid] > nums[mid+1]:数据是递减的,下坡
- nums[mid] < nums[mid+1]:数据是递增的,上坡
- L==R时,到达山峰
def fun(nums):
L, R = 0, len(nums)
while L < R:
mid = (L + R) //2
if nums[mid] > nums[mid+1]:
R = mid
else:
L = mid + 1
return L相反,如果数组是“山谷”型,求最小值的下标则相反:
def fun(nums):
L, R = 0, len(nums)
while L < R:
mid = (L + R) //2
if nums[mid] > nums[mid+1]:
L = mid + 1
else:
R = mid
return L峰值元素是指其值大于左右相邻值的元素。
给你一个输入数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
示例 1:
输入:nums = [1,2,3,1] 输出:2 解释:3 是峰值元素,你的函数应该返回其索引 2。 示例 2:
输入:nums = [1,2,1,3,5,6,4] 输出:1 或 5 解释:你的函数可以返回索引 1,其峰值元素为 2; 或者返回索引 5, 其峰值元素为 6。
O(logN)一般考虑二分搜索。有如下规律:
- 规律一:如果nums[i] > nums[i+1],则在i之前一定存在峰值元素
- 规律二:如果nums[i] < nums[i+1],则在i+1之后一定存在峰值元素
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
if len(nums) < 2: return 0
L, R = 0, len(nums)-1
while L < R:
mid = (L + R)//2
if nums[mid] > nums[mid+1]:
R = mid
else:
L = mid + 1
return L给你一个 山脉数组 mountainArr,请你返回能够使得 mountainArr.get(index) 等于 target 最小 的下标 index 值。
如果不存在这样的下标 index,就请返回 -1。
何为山脉数组?如果数组 A 是一个山脉数组的话,那它满足如下条件:
首先,A.length >= 3
其次,在 0 < i < A.length - 1 条件下,存在 i 使得:
A[0] < A[1] < ... A[i-1] < A[i] A[i] > A[i+1] > ... > A[A.length - 1]
你将 不能直接访问该山脉数组,必须通过 MountainArray 接口来获取数据:
MountainArray.get(k) - 会返回数组中索引为k 的元素(下标从 0 开始) MountainArray.length() - 会返回该数组的长度
注意:
对 MountainArray.get 发起超过 100 次调用的提交将被视为错误答案。此外,任何试图规避判题系统的解决方案都将会导致比赛资格被取消。
为了帮助大家更好地理解交互式问题,我们准备了一个样例 “答案”:https://leetcode-cn.com/playground/RKhe3ave,请注意这 不是一个正确答案。
示例 1:
输入:array = [1,2,3,4,5,3,1], target = 3 输出:2 解释:3 在数组中出现了两次,下标分别为 2 和 5,我们返回最小的下标 2。
与上一题类似:
class Solution:
def binary_search(self, mountain_arr: 'MountainArray', target: int, L: int, R: int, sign: int ) -> int:
# *(-1) 就可以处理单调递减的序列了 类似的**有:排序时x --> -x python 入堆时,x -->(-x)就是最大堆
target = sign * target
while L <= R:
mid = (L + R) >> 1
cur = sign * mountain_arr.get(mid)
if cur == target:
return mid
elif cur < target:
L = mid + 1
else:
R = mid - 1
return -1
def findInMountainArray(self, target: int, mountain_arr: 'MountainArray') -> int:
L = 0
R = mountain_arr.length() - 1
while L < R:
mid = (L + R) >> 1
if mountain_arr.get(mid) < mountain_arr.get(mid + 1):
L = mid + 1
else:
R = mid
peak_idx = L # 找到峰值(最大值),再左右两侧查找target
res = self.binary_search(mountain_arr, target, 0, peak_idx, 1)
if res != -1:
return res
return self.binary_search(mountain_arr, target, peak_idx + 1, mountain_arr.length() - 1, -1)给定一个排序好的数组 arr ,两个整数 k 和 x ,从数组中找到最靠近 x(两数之差最小)的 k 个数。返回的结果必须要是按升序排好的。
整数 a 比整数 b 更接近 x 需要满足:
- |a - x| < |b - x| 或者
- |a - x| == |b - x| 且 a < b
示例 1:
输入:arr = [1,2,3,4,5], k = 4, x = 3 输出:[1,2,3,4] 示例 2:
输入:arr = [1,2,3,4,5], k = 4, x = -1 输出:[1,2,3,4]
class Solution:
def findClosestElements(self, arr: List[int], k: int, x: int) -> List[int]:
L, R = 0, len(arr)-1
# 根据距离值大小回缩
while (R - L) >= k:
if (x - arr[L]) < (arr[R]-x): # 右侧距离更大,去掉右侧值
R -= 1
elif (x - arr[L]) > (arr[R]-x): # 左侧距离更大,去掉左侧值
L += 1
else: # 相等情况下去掉右侧值
R -=1
return arr[L:R+1]给你一个 n x n 矩阵 matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。 请注意,它是 排序后 的第 k 小元素,而不是第 k 个 不同 的元素。
示例 1:
输入:matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8 输出:13 解释:矩阵中的元素为 [1,5,9,10,11,12,13,13,15],第 8 小元素是 13 示例 2:
输入:matrix = [[-5]], k = 1 输出:-5
二分查找:
- 左右指针(left、right)分别初始化为矩阵左上角最小值和矩阵右下角最大值
- 若不大于中间值mid的数比k多,说明mid可能取大了,因为存在重复数字,但也可能当前mid其实就是我们想要的值,因此令right = mid
- 若不大于中间值mid的数正好k个,当前mid也可能偏大了,因为当前mid可能不在矩阵中,因此还是令right = mid
- 若不大于中间值mid的数比k少,说明mid取小了,令left = mid + 1
- 当left == right时,循环结束,返回left
注意循环条件是 left < right 而不是 left <= right,因为第k小元素一定存在,所以当left == right时就是找到了想要的值了;如果是left <= right的话循环是无法终止的,因为这样的话永远会有left = right = mid。
class Solution:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
def count(mid):
i, j = n-1, 0
num = 0
while 0 <= i and j < n:
if matrix[i][j] <= mid:
num += i + 1
j += 1
else:
i -= 1
return num
n = len(matrix)
L, R = matrix[0][0], matrix[-1][-1]
while L < R:
mid = (L+R)//2
if count(mid) >= k:
R = mid
else:
L = mid + 1
return L几乎每一个人都用 乘法表。但是你能在乘法表中快速找到第k小的数字吗?
给定高度m 、宽度n 的一张 m * n的乘法表,以及正整数k,你需要返回表中第k 小的数字。
例 1:
输入: m = 3, n = 3, k = 5 输出: 3 解释: 乘法表: 1 2 3 2 4 6 3 6 9
第5小的数字是 3 (1, 2, 2, 3, 3).
与上一题类似:
class Solution:
def findKthNumber(self, m: int, n: int, k: int) -> int:
def count(mid):
i, j, num = 0, n-1, 0
while i < m and j>=0:
if (i+1)*(j+1) <= mid:
num += j+1
i +=1
else:
j -=1
return num
L, R = 1, m*n
while L < R:
mid = (L+R)//2
if count(mid) >= k:
R = mid
else:
L = mid + 1
return L珂珂喜欢吃香蕉。这里有 N 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 H 小时后回来。
珂珂可以决定她吃香蕉的速度 K (单位:根/小时)。每个小时,她将会选择一堆香蕉,从中吃掉 K 根。如果这堆香蕉少于 K 根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 H 小时内吃掉所有香蕉的最小速度 K(K 为整数)。
示例 1:
输入: piles = [3,6,7,11], H = 8 输出: 4 示例 2:
输入: piles = [30,11,23,4,20], H = 5 输出: 30 示例 3:
输入: piles = [30,11,23,4,20], H = 6 输出: 23
class Solution:
def minEatingSpeed(self, piles: List[int], H: int) -> int:
if not piles: return 0
min_, max_ = 1, max(piles)
def cal(s): # 计算需要多少时间
times = [it//s for it in piles]
rest = [int(it%s > 0) for it in piles]
hour = sum(times+rest)
return hour
while min_ < max_:
mid = (min_+max_)//2
hour_tmp = cal(mid)
if hour_tmp > H:
min_ = mid + 1
else:
max_ = mid
return min_题目描述: 假设我们在一条水平数轴上,列表 stations 来表示各个加油站的位置,加油站分别在 stations[0], stations[1], …, stations[N-1] 的位置上,其中 N = stations.length。 现在我们希望增加 K 个新的加油站,使得相邻两个加油站的距离 D 尽可能的最小,请你返回 D 可能的最小值。
示例: 输入:stations = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], K = 9 输出:0.500000
注: stations.length 是在范围 [10, 2000] 内的整数 stations[i] 是在范围 [0, 10^8] 内的整数 K 是在范围 [1, 10^6] 内的整数 在 10^-6 以内的正确值会被视为正确的答案
class Solution:
def minmaxGasDist(self, stations: List[int], k: int) -> float:
distances = []
for i in range(len(stations) - 1):
distances.append(stations[i + 1] - stations[i])
left, right = 0, max(distances)
while right - left > pow(10, -7):
mid = (left + right) / 2
need = 0
for distance in distances:
a, b = divmod(distance, mid)
need += (a - 1) + (1 if b > 0 else 0)
if need <= k:
right = mid
else:
left = mid
return (left + right) / 234. 在排序数组中查找元素的第一个和最后一个位置/字节2面-有重复数的二分查找
含有重复数的数组,给定target,找出其Index,如果重复,找出最左侧的index和最右侧的index,单独一个的,返回index两次,不存在,返回(-1,-1),如:
num=[1, 2, 3, 3, 3, 4, 5],target=3,返回(2,4)
num=[1, 2, 3, 3, 3, 4, 5],target=2,返回(1,1)
num=[1, 2, 3, 3, 3, 4, 5],target=6,返回(-1,-1)
利用二分**先找其左边界,再找其右边界即可,注意找左边界的时候,由右侧逼近;找右边界的时候,由左侧逼近,即可。
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
if not nums: return (-1, -1)
n = len(nums)
L, R, ans = 0, n-1, -1
# 找左边界,右侧逼近
while L<R:
mid = (L+R)//2
if nums[mid] >= target:
R = mid
else:
L = mid + 1
if nums[L] != target:
return (-1, -1)
# 确定左侧边界
ans, R = L, n
# 找有边界,左侧逼近
while L < R:
mid = (L+R)//2
if nums[mid] <= target:
L = mid + 1
else:
R = mid
return (ans, L-1)利用二分法,先找出一个target,然后向两边扩散,返回两端点值:
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
if not nums: return (-1, -1)
n = len(nums)
L, R = 0, n-1
while L<=R:
mid = (L+R)//2
if nums[mid] == target:
L = R = mid
if mid == 0:
L = 0
elif mid == (n-1):
R = n-1
while 0< L and nums[L-1]==target :
L -= 1
while R < (n-1) and nums[R+1]==target:
R += 1
return (L, R)
elif nums[mid] < target:
L = mid+1
else:
R = mid-1
return (-1, -1)给定一个非负整数数组 nums 和一个整数 m ,你需要将这个数组分成 m 个非空的连续子数组。
设计一个算法使得这 m 个子数组各自和的最大值最小。
示例 1:
输入:nums = [7,2,5,10,8], m = 2 输出:18 解释: 一共有四种方法将 nums 分割为 2 个子数组。 其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。 因为此时这两个子数组各自的和的最大值为18,在所有情况中最小。 示例 2:
输入:nums = [1,2,3,4,5], m = 2 输出:9 示例 3:
输入:nums = [1,4,4], m = 3 输出:4
解题思路
- 初始化,left为nums的最大值,right为nums的和,那么我们要求的结果res一定在[left, right]中。
- 找区间的中点mid,调用函数check,来康康:如果要求每个子数组的和不超过mid,是否能将nums分成m个子数组。
- 如果可以,res一定在[left, mid]中。
- 如果8行,res一定在(mid, right]中。
class Solution:
def splitArray(self, nums: List[int], m: int) -> int:
if len(nums)==m: return max(nums)
left, right = max(nums), sum(nums) # 初始化查找区间
while left < right:
mid = (left + right) // 2 # 中间值
tmp, count = 0, 1
for it in nums: # 在中间值的情况下,计算能分成几组
tmp += it
if tmp > mid:
tmp = it
count += 1
if count > m: # 分组个数大于m,说明mid值太小; 否则太大
left = mid + 1
else:
right = mid
return left给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
输入:nums1 = [1,3], nums2 = [2] 输出:2.00000 解释:合并数组 = [1,2,3] ,中位数 2
取两个数组中的第k/2个元素进行比较,如果数组1的元素小于数组2的元素,则说明数组1中的前k/2个元素不可能成为第k个元素的候选,所以将数组1中的前k/2个元素去掉,组成新数组和数组2求第k-k/2小的元素,因为我们把前k/2个元素去掉了,所以相应的k值也应该减小。另外就是注意处理一些边界条件问题,比如某一个数组可能为空或者k为1的情况。
class Solution(object):
def findMedianSortedArrays(self, nums1, nums2):
l1, l2 = len(nums1), len(nums2)
left, right = (l1+l2+1)//2, (l1+l2+2)//2 # 找到两个数, 对奇偶数均适用
return (self.findMaxK(nums1,nums2,left) + self.findMaxK(nums1,nums2,right))/2 # 取均值
def findMaxK(self, nums1, nums2, k):
len1, len2 = len(nums1), len(nums2)
if len2==0:
return nums1[k-1]
if len1==0:
return nums2[k-1]
if k == 1:
return min(nums1[0], nums2[0])
i, j = min(k//2, len1)-1, min(k//2,len2)-1
# 数组1的元素小于数组2的元素,说明数组1中的前k/2个元素不可能成为第k个元素的候选
if nums1[i] <= nums2[j]:
# 将数组1中的前k/2个元素去掉,组成新数组和数组2求第k-k/2小的元素
return self.findMaxK(nums1[i+1:], nums2, k-i-1)
else:
return self.findMaxK(nums1, nums2[j+1:], k-j-1)快速排序:
import random
class Solution(object):
def sort_num(self, n_list):
if len(n_list) < 2: # 基线条件 列表中只有1个或0个元素
return n_list
else: # 递归条件
index = random.randint(0, len(n_list)-1)
in_num = n_list[index]
small = [item for item in (n_list[:index]+n_list[index+1:]) if item<in_num]
large = [item for item in (n_list[:index]+n_list[index+1:]) if item>in_num]
return self.sort_num(small)+[in_num]+self.sort_num(large)
nums=[2,7,11,3,1,5,15]
s = Solution()
print(s.sort_num(nums))
# 如果存在元素重复时
from random import randint
class Solution(object):
def sortArray(self, nums):
if len(nums)<2:
return nums
index = randint(0, len(nums)-1)
key = nums[index]
small = [item for item in (nums[:index]+nums[index:]) if item <key]
middle = [item for item in (nums[:index]+nums[index:]) if item == key]
large = [item for item in (nums[:index]+nums[index:]) if item >key]
return self.sortArray(small) + middle + self.sortArray(large)给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n,这样它就有足够的空间保存来自 nums2 的元素。
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6]
归并排序中的合并部分程序:
class Solution(object):
def merge(self, nums1, m, nums2, n):
res = []
left, right = nums1[:m], nums2[:n]
while len(left) > 0 and len(right) > 0:
if left[0] <= right[0]:
res.append(left.pop(0))
else:
res.append(right.pop(0))
return res + left + right双指针:
class Solution(object):
def merge(self, nums1, m, nums2, n):
#i为nums1的m开始索引, j为nums2的n开始索引,idx为修改nums1的开始索引,然后从nums1末尾开始往前遍历
i, j, idx = m-1, n-1, len(nums1)-1
#按从大到小,从后往前修改nums1的值,每次都赋值为nums1和nums2的当前索引的较大值,然后移动索引
while i >=0 and j >=0:
#如果nums1[i] >= nums2[j],则先赋值为nums1[i],i索引减少
if nums1[i] >= nums2[j]:
nums1[idx] = nums1[i]
i -= 1
else:
#如果nums1[i] <= nums2[j],则先赋值为nums2[j],j索引减少
nums1[idx] = nums2[j]
j -= 1
#当前nums1修改索引减少1
idx -=1
# nums2没有遍历完n个,则继续遍历,直到n个完成
while j>=0:
nums1[idx] = nums2[j]
j -= 1
idx -= 1
return nums1在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
输入: [7,5,6,4] 输出: 5
主要思路是归并排序,归并排序的过程中会将左右两部分合并成一个有序的部分,当满足左侧元素大于右侧时,计算其逆序数即可,最后采用一个全局的变量,对其统计,最后返回即可。相当于对原数组排序后,同时返回一个逆序对的统计值。
class Solution(object):
def reversePairs(self, nums):
if len(nums)<=1:
return 0
self.count = 0 # 全局统计值
self.merge_sort(nums)
return self.count
def merge_sort(self, alist):
if len(alist)==1:
return alist
mid = len(alist)//2
left = self.merge_sort(alist[:mid]) # 递归进行分治与合并
right = self.merge_sort(alist[mid:])
return self.merge(left, right)
def merge(self, left, right):
result = []
while len(left)>0 and len(right)>0:
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
self.count += len(left) # right[0]小于left[0],那么right[0]小于整个left值,因为left是从小到大排序的,后面的值left[0:]均大于left[0],这些都是逆数对
return result + left + right给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入:nums = [5,2,6,1] 输出:[2,1,1,0] 解释: 5 的右侧有 2 个更小的元素 (2 和 1) 2 的右侧仅有 1 个更小的元素 (1) 6 的右侧有 1 个更小的元素 (1) 1 的右侧有 0 个更小的元素
与上一题类似,解答本题需要添加的部分
- 记录每个元素在原列表中的位置, 通过nums = list(enumerate(nums))实现
- 合并列表时记录逆序数对的对数,每次添加left[i]时,在此之前添加的right[j]就和left[i]构成了逆序数对 (在数组右侧却先添加)。
对于本题目,因为需要得到右侧严格小于的数字的个数,所以排序时候的判断必须是left[i][1]<=right[j][1],否则会出错。例如 nums=[-1,-1],如果按照小于来计算,那么 right首先走到尽头,会使得cnt[nums[1][0]]=1.
class Solution:
def countSmaller(self, nums: List[int]) -> List[int]:
if len(nums)<=1:
return [0]
self.res = [0]*len(nums)
nums = list(enumerate(nums)) # 为了记住每个元素在原数组中的位置,元组形式
self.merge_sort(nums)
return self.res
def merge_sort(self, alist):
if len(alist)==1:
return alist
mid = len(alist)//2
left = self.merge_sort(alist[:mid]) # 递归进行分治与合并
right = self.merge_sort(alist[mid:])
return self.merge(left, right)
def merge(self, left, right):
tmp, i, j = [], 0, 0
while len(left)>i or len(right)>j:
if j == len(right) or i < len(left) and left[i][1] <= right[j][1]:
tmp.append(left[i])
self.res[left[i][0]] += j
i += 1
else:
tmp.append(right[j])
j += 1
return tmp如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。 子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1: 输入:nums = [1,7,4,9,2,5] 输出:6 解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。 示例 2: 输入:nums = [1,17,5,10,13,15,10,5,16,8] 输出:7 解释:这个序列包含几个长度为 7 摆动序列。 其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
主要采用贪心算法,
用示例二来举例,如图所示:
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)
这就是贪心所贪的地方,让峰值尽可能的保持峰值,然后删除单一坡度上的节点。
针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即preDiff = 0,如图:
针对以上情形,result初始为1(默认最右面有一个峰值),此时curDiff > 0 && preDiff <= 0,那么result++(计算了左面的峰值),最后得到的result就是2(峰值个数为2即摆动序列长度为2)
class Solution:
def wiggleMaxLength(self, nums):
preC, curC, res = 0, 0, 1 #题目里nums长度大于等于1,当长度为1时,其实到不了for循环里去,所以不用考虑nums长度
for i in range(len(nums) - 1):
curC = nums[i + 1] - nums[i]
if curC * preC <= 0 and curC !=0: #差值为0时,不算摆动
res += 1
preC = curC #如果当前差值和上一个差值为一正一负时,才需要用当前差值替代上一个差值
return res利用摆动序列,波峰和波谷的差值最多为1的特点。一次遍历,常数空间。
class Solution:
def wiggleMaxLength(self, nums):
up ,down = 1,1
if len(nums)<2:return len(nums)
for i in range(1,len(nums)):
if nums[i]>nums[i-1]:
up = down+1
if nums[i]<nums[i-1]:
down = up+1
return max(up,down)有N个箱子排成N行,通过多次推动将每个箱子推动到每行指定位置,位置用数字表示,初始位置为0。例如,0 1 2 3 0 2 1 2 1,每次至推动一个位置,可一次操作多行,至少要几次,上面是6次,连续时,不包含0
nums = list(map(int, input().strip().split()))
def fun(nums):
if not nums: return 0
res = 0
for i in range(1, len(nums)):
if nums[i] - nums[i-1] > 0:
res += nums[i] - nums[i-1]
return res
print(fun(nums))不必排序,分而治之,在最大、最小里面找:
class Solution(object):
def findKthLargest(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
if k > len(nums):
return
index = randint(0,len(nums)-1)
pivot = nums[index]
small=[i for i in (nums[:index]+nums[index+1:])if i < pivot] # 比pivot都小的放入small
large=[i for i in (nums[:index]+nums[index+1:])if i >= pivot] # 比pivot都大的放入large
if k-1 == len(large): # 所有比第k个数大的集合
return pivot
elif k-1<len(large): # 如果小于,说明large中元素多了,在large中
return self.findKthLargest(large, k)
if k-1 > len(large): # 如果大于,说明large中元素少了,在small中
return self.findKthLargest(small, k-1-len(large))输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
输入:arr = [3,2,1], k = 2 输出:[1,2] 或者 [2,1] 示例 2:
输入:arr = [0,1,2,1], k = 1 输出:[0]
class Solution:
def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
arr.sort()
if k>=len(arr):
return arr
else:
return arr[:k]给定一个无序的数组,找出数组在排序之后,相邻元素之间最大的差值。
如果数组元素个数小于 2,则返回 0。
示例 1:
输入: [3,6,9,1] 输出: 3 解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。 示例 2:
输入: [10] 输出: 0 解释: 数组元素个数小于 2,因此返回 0。 说明:
- 你可以假设数组中所有元素都是非负整数,且数值在 32 位有符号整数范围内。
- 请尝试在线性时间复杂度和空间复杂度的条件下解决此问题。O(n)
简单排序,可能不符合要求:
class Solution:
def maximumGap(self, nums: List[int]) -> int:
L = len(nums)
if L <2 : return 0
nums.sort()
res = 0
for i in range(1, L):
res = max(res, nums[i]-nums[i-1])
return res采用基数排序:
class Solution:
def maximumGap(self, nums: List[int]) -> int:
L = len(nums)
if L <2 : return 0
for i in range(len(str(max(nums)))): # 以最大数,获得数据的最大长度
buckets=[[] for _ in range(10)] # 个位数
for num in nums: # 按照个位数进行排序,个位为0的放在buckets的第0个list中
buckets[num//(10**i)%10].append(num)
nums=[num for bucket in buckets for num in bucket] # 将buckets又变成列表
# 对排序好的数据计算差值
return max([0]+[nums[i+1]-nums[i] for i in range(len(nums)-1)])在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
给你一个数组 points ,其中 points [i] = [xstart,xend] ,返回引爆所有气球所必须射出的最小弓箭数。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]] 输出:2 解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球 示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]] 输出:4 示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]] 输出:2
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
if len(points) < 1: return 0
points.sort(key=lambda x: x[1]) # 右端排序
res,end = 1, points[0][1]
for i in range(1, len(points)):
if points[i][0] > end: # 气球i和气球i-1不挨着,注意这里不是>=
res += 1
end = points[i][1] # 更新重叠气球最小右边界
return res给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。 示例 1:
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。 示例 2:
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
将问题转化为,求不重叠的区间有几个,再用个数减去即可。
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
if len(intervals) < 1: return 0
intervals.sort(key=lambda x: x[1]) # 按end进行排序
res, end = 1, intervals[0][1]
for i in range(1, len(intervals)):
if intervals[i][0] >= end: # 区间不重叠的部分
res += 1
end = intervals[i][1]
return (len(intervals) - res) 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6]. 示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
如上题,但是按照初始点排序。
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
if len(intervals) < 1: return None
intervals.sort(key=lambda x: x[0])
res = [intervals[0]]
for i in range(1, len(intervals)):
tmp = res[-1]
if intervals[i][0] <= tmp[1]: # 起点小于上一次的终点,更新起始点和终点
res[-1] = [tmp[0], max(tmp[1], intervals[i][1])]
else:
res.append(intervals[i])
return res给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾勒出来的矩形的最大面积。
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
单调栈:从栈底元素到栈顶元素呈单调递增或单调递减,栈内序列满足单调性的栈。
class Solution:
def largestRectangleArea(self, heights):
res = 0
heights = [0] + heights +[0]
size = len(heights)
stack = [0]
for i in range(1, size):
while heights[i] < heights[stack[-1]]: # 如果右侧的值,小于栈中末尾的,则停止,计算矩形面积
height = heights[stack.pop()] # 栈中末尾值
width = i - stack[-1] -1 # 当前位置,减去其左侧的位置,取宽度
res = max(res, height*width)
stack.append(i)
return res
heights = [2, 1, 5, 6, 2, 3]
s = Solution()
print(s.largestRectangleArea(heights)) 给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出:6
在上一题求柱状图中最大的矩形的基础上,对矩阵,逐行按照柱状图求解。
class Solution:
def maximalRectangle(self, matrix):
if not matrix:
return 0
m, n = len(matrix), len(matrix[0])
heights = [0]*n # 逐行对列统计个数
res = 0
for i in range(m):
for j in range(n):
if matrix[i][j] == "0": # 下层出现为0,需要对原来的统计置0
heights[j] = 0
else:
heights[j] +=1 # 统计柱子高度
res = max(res, self.largestRectangleArea(heights))
return res
def largestRectangleArea(self, heights): # 柱状图中最大的矩形
res = 0
heights = [0] + heights + [0]
size = len(heights)
stack = [0]
for i in range(1, size):
while heights[i] < heights[stack[-1]]:
height = heights[stack.pop()]
width = i -stack[-1]-1
res = max(res, height*width)
stack.append(i)
return res
matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
s = Solution()
print(s.maximalRectangle(matrix)) 另一解法:二进制的&运算求矩形高度,>>运算来计算矩形宽度,然后每一行都遍历一遍,得出最大值。
class Solution:
def maximalRectangle(self, matrix):
if not matrix or not matrix[0]:
return 0
nums = [int(''.join(row), base=2) for row in matrix] #先将每一行变成2进制的数字
ans, N = 0, len(nums)
for i in range(N):#遍历每一行,求以这一行为第一行的最大矩形
j, num = i, nums[i]
while j < N: #依次与下面的行进行与运算。
num = num & nums[j] #num中为1的部分,说明上下两行该位置都是1,相当于求矩形的高,高度为j-i+1
# print('num=',bin(num))
if not num: #没有1说明没有涉及第i到第j行的竖直矩形
break
width, curnum = 0, num
while curnum:
#将cursum与自己右移一位进行&操作。如果有两个1在一起,那么cursum才为1,相当于求矩形宽度
width += 1
curnum = curnum & (curnum >> 1)
# print('curnum',bin(curnum))
ans = max(ans, width * (j-i+1))
# print('i','j','width',i,j,width)
# print('ans=',ans)
j += 1
return ans
matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
s = Solution()
print(s.maximalRectangle(matrix))给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

class Solution(object):
def rotate(self, matrix):
n = len(matrix)
matrix_new = [[0]*n for _ in range(n)]
for i in range(n):
for j in range(n):
matrix_new[j][n-1-i]=matrix[i][j]
matrix[:] = matrix_new
return matrixclass Solution:
def rotate(self, matrix):
n = len(matrix)
# 水平翻转
for i in range(n // 2):
for j in range(n):
matrix[i][j], matrix[n - i - 1][j] = matrix[n - i - 1][j], matrix[i][j]
# 主对角线翻转
for i in range(n):
for j in range(i):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]编写一个高效的算法来判断
$m \times n$ 矩阵中,是否存在一个目标值。该矩阵具有如下特性:每行中的整数从左到右按升序排列。 每行的第一个整数大于前一行的最后一个整数。
示例 1:

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true
240题
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。 每列的元素从上到下升序排列。
从左下角或右上角开始查找
遍历的方式,是从左上或有右下角开始,但是并未使用矩阵有序的性质,时间复杂度为O(M∗N)。
如果我们从右上角开始遍历:
- 如果要搜索的 target 比当前元素大,那么让行增加;
- 如果要搜索的 target 比当前元素小,那么让列减小;
class Solution(object):
def searchMatrix(self, matrix, target):
m, n = len(matrix), len(matrix[0])
i, j = 0, n-1
while i < m and j >=0:
if matrix[i][j] < target:
i +=1
elif matrix[i][j] > target:
j -=1
else:
return True
return False二分法
既然是有序数组,那么可以考虑二分法,可将整个数组看成一个数列来处理。
class Solution(object):
def searchMatrix(self, matrix, target):
m, n = len(matrix), len(matrix[0])
left, right = 0, n*m-1
while left<=right:
mid = left + (right - left)//2
value = matrix[mid // n][mid % n]
if value < target:
left = mid + 1
elif value > target:
right = mid - 1
else:
return True
return False给定一个含有 M x N 个元素的矩阵(M 行,N 列),请以对角线遍历的顺序返回这个矩阵中的所有元素,对角线遍历如下图所示。
示例:
输入: [ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 9 ] ]
输出: [1,2,4,7,5,3,6,8,9]
解释:

思路:
'''
每层的索引和相等:
1. 假设矩阵无限大;
2. 索引和为{偶}数,向上遍历,{横}索引值递减,遍历值依次是(x,0),(x-1,1),(x-2,2),...,(0,x)
3. 索引和为{奇}数,向下遍历,{纵}索引值递减,遍历值依次是(0,y),(1,y-1),(2,y-2),...,(y,0)
每层的索引和:
0: (00)
1: (01)(10)
2: (20)(11)(02)
3: (03)(12)(21)(30)
4: (40)(31)(22)(13)(04)
5: (05)(14)(23)(32)(41)(50)
6: (60)(51)................(06)
按照“层次”遍历,依次append在索引边界内的值即可
'''class Solution(object):
def findDiagonalOrder(self, mat):
"""
:type mat: List[List[int]]
:rtype: List[int]
"""
n, m = len(mat) - 1 , len(mat[0]) - 1 # 横轴 索引最大值n, 纵轴 索引最大值m
level = n + m + 1 # 层数等于横纵最大索引之和 + 1
res = []
for x in range(level): # 层数值
#索引和为{偶}数,向上遍历,{横}索引值递减,遍历值依次是(x,0),(x-1,1),(x-2,2),...,(0,x),不要索引出界的,即可
if x%2==0:
for i in range(x, -1, -1):
j = x - i
if i <=n and j <=m:
res.append(mat[i][j])
elif j > m: # j递增,超出纵轴索引
break
#索引和为{奇}数,向下遍历,{纵}索引值递减,遍历值依次是(0,y),(1,y-1),(2,y-2),...,(y,0),不要索引出界的,即可
else:
for j in range(x, -1, -1):
i = x - j
if i <=n and j <=m:
res.append(mat[i][j])
elif i > n: # i递增,超出横轴索引
break
return res简化代码:
'''
以3*4为例
0:
(00)
1:
(01)
(10)
2:
(20)
(11)
(02)
3:
(03)
(12)
(21)
4:
(22)
(13)
5:
(23)
'''
class Solution(object):
def findDiagonalOrder(self, mat):
"""
:type mat: List[List[int]]
:rtype: List[int]
"""
m, n, res = len(mat), len(mat[0]), []
level = n + m + 1 # 层数
for i in range(level):
#左上三角:层数i小于纵轴时,范围是从0开始,到横轴最大值m
#右下三角:层数i大于纵轴时,范围是从i+1-n开始,到横轴最大值m
tmp = [mat[j][i-j] for j in range(max(0, i+1-n), min(i+1, m))]
res += tmp if i%2 else tmp[::-1] # 奇数层则反向排序
return res给你一个二维整数数组 matrix, 返回 matrix 的 转置矩阵 。
矩阵的 转置 是指将矩阵的主对角线翻转,交换矩阵的行索引与列索引。
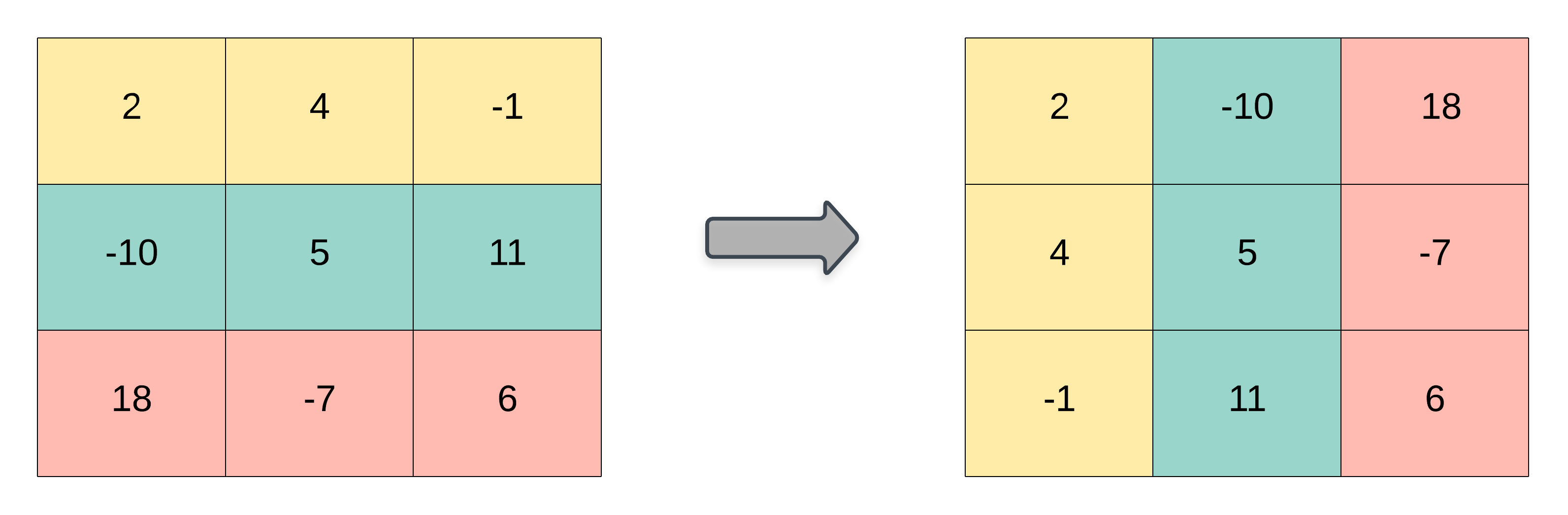
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[1,4,7],[2,5,8],[3,6,9]] 示例 2:
输入:matrix = [[1,2,3],[4,5,6]] 输出:[[1,4],[2,5],[3,6]]
class Solution:
def transpose(self, matrix: List[List[int]]) -> List[List[int]]:
if not matrix: return None
m, n = len(matrix), len(matrix[0])
matrix_new = [[0]*m for _ in range(n)]
for i in range(m):
for j in range(n):
matrix_new[j][i] = matrix[i][j]
return matrix_new给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
进阶:
一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。 一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。 你能想出一个仅使用常量空间的解决方案吗?
示例 1:

输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
class Solution:
def setZeroes(self, matrix):
"""
Do not return anything, modify matrix in-place instead.
"""
if not matrix: return None
m, n = len(matrix), len(matrix[0])
for i in range(m):
for j in range(n):
if matrix[i][j] == 0:
for l in range(n):
if matrix[i][l] !=0:
matrix[i][l] = '0'
for k in range(m):
if matrix[k][j] != 0:
matrix[k][j] = '0'
for i in range(m):
for j in range(n):
if matrix[i][j] == '0': matrix[i][j]=0
return matrix根据 百度百科 ,生命游戏,简称为生命,是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态:1 即为活细胞(live),或 0 即为死细胞(dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡; 如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活; 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡; 如果死细胞周围正好有三个活细胞,则该位置死细胞复活; 下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态,返回下一个状态。
示例 1:

输入:board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]] 输出:[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
m,n = len(board),len(board[0])
board_copy = copy.deepcopy(board)
# 求位置为 i,j 的细胞附近的活细胞数目
def around(i,j):
num_alive = 0
dirs=[[-1, -1], [-1, 0], [-1, 1], [0, -1],[0, 1], [1, -1], [1, 0], [1, 1]]
for dx, dy in dirs:
i_new, j_new = i+dx, j+dy
if 0<=i_new<m and 0<=j_new<n:
if board_copy[i_new][j_new]==1: num_alive+=1
return num_alive
# 遍历所有细胞
for i in range(m):
for j in range(n):
alive = around(i, j)
if alive>3 or alive<2:
board[i][j]=0
elif alive==3:
board[i][j]=1
return board 暴力计算:$C[i][k] += A[i][j]*B[j][k]$
class Solution:
def multiply(self, A, B) -> List[List[int]]:
size1, size2 = len(A), len(B[0]) # A的行数 和 B的列数
size3 = len(A[0]) # A的列数和B的行数相等
ans = [[0] * size2 for _ in range(size1)]
for i1 in range(size1):
for i2 in range(size2):
for i3 in range(size3):
ans[i1][i2] += A[i1][i3] * B[i3][i2]
return ans利用hashmap来储存非0元素。这应该是面试中比较标准的解法。一个encode来把sparse_matrx转换成dense_matrix。然后对dense_matrix做乘法,最后用decode把dense_matrix的结果转换为sparse_matrix的结果
class Solution:
def multiply(self, A: List[List[int]], B: List[List[int]]) -> List[List[int]]:
def encode(sparse_matrix):
dense_matrix = {}
for i in range(len(sparse_matrix)):
for j in range(len(sparse_matrix[0])):
if sparse_matrix[i][j]:
dense_matrix[(i,j)] = sparse_matrix[i][j]
return dense_matrix
def decode(dense_matrix,row,col):
sparse_matrix = [[0]*col for _ in range(row)]
for (i,j),val in dense_matrix.items():
sparse_matrix[i][j] = val
return sparse_matrix
A_dense = encode(A)
B_dense = encode(B)
ans_dense = collections.defaultdict(int)
for (i,j) in A_dense.keys():
for k in range(len(B[0])):
if (j,k) in B_dense:
ans_dense[(i,k)] += A_dense[(i,j)]*B_dense[(j,k)]
return decode(ans_dense,len(A),len(B[0]))输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]

输出:[1,2,3,6,9,8,7,4,5]
示例 2: 输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
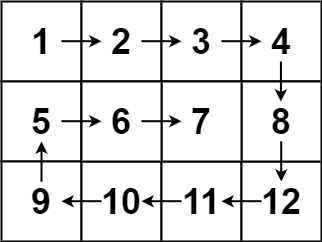
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
没有太多技巧,主要按照思路及规则完成。
沿着顺时针方向走(右->下->左->上->),毎走完一行或者一列后, 走过的对应边界也缩小, 不断循环,
以至最后边界无法再缩小时, 循环结束
比如,向右走完一行,上边界top下移一行;
向下走完一行,右边界right左移一行;
向左走完一行,下边界bottom上移一行;
向上走完一行,左边界left右移一行;class Solution(object):
def spiralOrder(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: List[int]
"""
if not matrix: return []
m, n = len(matrix), len(matrix[0])
top, bottom, left, right = 0, m-1, 0, n-1
res = []
while True:
# 向右走完一行,上边界top下移一行
for i in range(left, right+1):
res.append(matrix[top][i])
top +=1
if top > bottom: break
# 向下走完一行,右边界right左移一行
for i in range(top, bottom+1):
res.append(matrix[i][right])
right -=1
if left > right: break
# 向左走完一行,下边界bottom上移一行
for i in range(right, left-1, -1):
res.append(matrix[bottom][i])
bottom -=1
if top > bottom: break
# 向上走完一行,左边界left右移一行
for i in range(bottom, top-1, -1):
res.append(matrix[i][left])
left +=1
if left > right: break
return res给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:

输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]
跟上一题一样,按顺序保存即可。
class Solution(object):
def generateMatrix(self, n):
"""
:type n: int
:rtype: List[List[int]]
"""
if n == 1: return [[n]]
top, bottom, left, right = 0, n-1, 0, n-1
matrix = [[0]*n for _ in range(n)]
num = 1
while True:
# 向右走完一行,上边界top下移一行
for i in range(left, right+1):
matrix[top][i] = num
num += 1
top +=1
if top > bottom: break
# 向下走完一行,右边界right左移一行
for i in range(top, bottom+1):
matrix[i][right] = num
num += 1
right -=1
if left > right: break
# 向左走完一行,下边界bottom上移一行
for i in range(right, left-1, -1):
matrix[bottom][i] = num
num += 1
bottom -=1
if top > bottom: break
# 向上走完一行,左边界left右移一行
for i in range(bottom, top-1, -1):
matrix[i][left] = num
num += 1
left +=1
if left > right: break
return matrix请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图) 数独部分空格内已填入了数字,空白格用 '.' 表示。
注意:
一个有效的数独(部分已被填充)不一定是可解的。 只需要根据以上规则,验证已经填入的数字是否有效即可。
示例 1:
输入:board = [["5","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出:true
使用line、column,和子区域来分别保存元素,如果元素有重复的就返回false,否则返回true即可。在这里巧用了一下集合,判断某个元素是否在集合中时间复杂度是O(1),如果使用列表的话就是O(n)了。 其中划分子区域的技巧很巧妙,使用的是 pos = (i//3)*3 + j//3。
或者,将每行、每列、每个子区域,用一个列表储存,后用set()判断是否有重复(len(list)=len(set)是否相等)。
class Solution(object):
def isValidSudoku(self, board):
"""
:type board: List[List[str]]
:rtype: bool
"""
matrix_m = [set() for _ in range(len(board))] # 每行用一个set()
matrix_n = [set() for _ in range(len(board[0]))]# 每列用一个set()
matrix_a = [set() for _ in range(len(board))] # 每个子区域用一个set()
for i in range(len(board)):
for j in range(len(board[0])):
it = board[i][j]
pos = (i//3)*3 + j//3 # 子区域的位置
if it != '.':
# 判断是否有重复
if (it not in matrix_m[i]) and (it not in matrix_n[j]) and (it not in matrix_a[pos]):
matrix_m[i].add(it)
matrix_n[j].add(it)
matrix_a[pos].add(it)
else:
return False
return True请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图) 数独部分空格内已填入了数字,空白格用 '.' 表示。
注意:
一个有效的数独(部分已被填充)不一定是可解的。 只需要根据以上规则,验证已经填入的数字是否有效即可。
示例 1:
输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] 输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]] 解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
class Solution(object):
def solveSudoku(self, board):
"""
:type board: List[List[str]]
:rtype: None Do not return anything, modify board in-place instead.
"""
matrix_m = [set(range(1,10)) for _ in range(len(board))] # 每行用一个set()
matrix_n = [set(range(1,10)) for _ in range(len(board[0]))]# 每列用一个set()
matrix_a = [set(range(1,10)) for _ in range(len(board))] # 每个子区域用一个set()
empty = []
for i in range(len(board)):
for j in range(len(board[0])):
it = board[i][j]
if it !='.':
pos = (i//3)*3 + j//3 # 子区域的位置
matrix_m[i].remove(int(it)) # 删除已经存在的数字
matrix_n[j].remove(int(it))
matrix_a[pos].remove(int(it))
else:
empty.append((i,j)) # 保存需要添加的位置
def backtrace(idx):
if len(empty)==idx: return True # 处理完empty代表找到了答案
i, j = empty[idx]
pos = (i//3)*3 + j//3 # 子区域的位置
for item in matrix_m[i] & matrix_n[j] & matrix_a[pos]: # 三个位置的公共子集
matrix_m[i].remove(item)
matrix_n[j].remove(item)
matrix_a[pos].remove(item)
board[i][j] = str(item)
if backtrace(idx+1): # 如果正常就返回,否则就回溯
return True
else:
matrix_m[i].add(item)
matrix_n[j].add(item)
matrix_a[pos].add(item)
return False
backtrace(0)
return board给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。
丑数 就是只包含质因数 2、3 和/或 5 的正整数。
示例 1:
输入:n = 6 输出:true 解释:6 = 2 × 3
思路:对能被2,3,5整除的数不断除2,3,5,最后剩1就是,剩0就不是
class Solution(object):
def isUgly(self, n):
"""
:type n: int
:rtype: bool
"""
if n < 1: return False
while n % 2 ==0:
n = n/2
while n % 3 ==0:
n = n/3
while n % 5 ==0:
n = n/5
return n==1给你一个整数 n ,请你找出并返回第 n 个 丑数 。
丑数 就是只包含质因数 2、3 和/或 5 的正整数。
示例 1:
输入:n = 10 输出:12 解释:[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。 示例 2:
输入:n = 1 输出:1 解释:1 通常被视为丑数。
思路:由于是找出丑数序列中的第n个,因而需要生成该序列。采用穷举法,对每个数进行判断,必定会超出时间,因而另寻思路。
要生成第 n 个丑数,我们必须从第一个丑数 1 开始,向后逐渐的寻找。丑数只包含 2, 3,5 三个因子,所以生成方式就是在已经生成的丑数集合中乘以 [2, 3, 5] 而得到新的丑数。
现在的问题是在已经生成的丑数集合中,用哪个数字乘以 2? 用哪个数字乘以 3?用哪个数字乘以 5?
很显然的一个结论:用还没乘过 2 的最小丑数乘以 2;用还没乘过 3 的最小丑数乘以 3;用还没乘过 5 的最小丑数乘以 5。然后在得到的数字中取最小,就是新的丑数。
实现的方法是用动态规划(三个指针):
- 我们需要定义 3 个指针idx2, idx3,idx5 分别表示丑数集合中还没乘过 2,3,5 的丑数位置。
- 然后每次新的丑数 dp[i] = min(dp[idx2] * 2, dp[idx3] * 3, dp[idx5] * 5) 。
- 然后根据 dp[i] 是由 idx2, idx3,idx5 中的哪个相乘得到的,对应的把此 index + 1,表示还没乘过该 index 的最小丑数变大了。
class Solution(object):
def nthUglyNumber(self, n):
"""
:type n: int
:rtype: int
"""
res=[1]
id2 = id3 = id5 = 0
for i in range(n-1):
m = min(res[id2]*2, res[id3]*3, res[id5]*5) # 找到其中的最小数
res.append(m) # 排序插入
if m == res[id2]*2: # 判断是哪个质因数,其个数加1
id2 +=1
if m == res[id3]*3:
id3 +=1
if m == res[id5]*5:
id5 +=1
return res[n-1] # 返回值编写一段程序来查找第 n 个超级丑数。超级丑数是指其所有质因数都是长度为 k 的质数列表 primes 中的正整数。
示例:
输入: n = 12, primes = [2,7,13,19] 输出: 32 解释: 给定长度为 4 的质数列表 primes = [2,7,13,19],前 12 个超级丑数序列为:[1,2,4,7,8,13,14,16,19,26,28,32] 。
此题是上一题的升级版,即质因数是变化的,那么用一个数组来存储其指针即可。
class Solution(object):
def nthSuperUglyNumber(self, n, primes):
"""
:type n: int
:type primes: List[int]
:rtype: int
"""
res, k = [1], len(primes) # k是质因数的个数
dp = [0 for _ in range(k)] # 质因数指针数组
for i in range(n-1):
m = min([res[dp[j]]*primes[j] for j in range(k)]) # 查询最小值
res.append(m) # 排序插入
for j in range(k):
if m == res[dp[j]]*primes[j]: # 判断是哪个质因数,其个数加1
dp[j] += 1
return res[n-1]统计所有小于非负整数 n 的质数的数量。
示例 1:
输入:n = 10 输出:4 解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
埃氏筛选法,关键**是:当找到一个质数,则将其所有整数倍的数全部标记为合数。
解释:对于质数x,其整数倍2x、3x、4x、...都是合数,可以被x整除;对于合数y,一定存在一个比y小的质数x可以整除y。
遍历时可以优化:
- 第一层循环不用遍历到n-1,只需遍历到sqrt(n)即可。
- 第二层循环不用从i*2开始遍历,从$i^2$开始遍历即可,因为$i^2$之前的i的整数倍已经被其他更小的质数标记过了。
class Solution:
def countPrimes(self, n):
is_primes = [1 for _ in range(2, n)]
for i in range(2, int(n**0.5)+1):
if is_primes[i-2]:
for j in range(i*i, n, i):
is_primes[j-2] = 0
return sum(is_primes)你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。 请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
输入:numCourses = 2, prerequisites = [[1,0],[0,1]] 输出:false 解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
正常思路,超时:
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
class_dict = {item[0]:item[1] for item in prerequisites}
for item in prerequisites:
tmp = []
class_ = item[1]
tmp.append(item[0])
while class_ in class_dict.keys():
tmp.append(class_)
if class_dict[class_] in tmp:
return False
else:
class_ = class_dict[class_]
return True考察拓扑排序:入度表BFS法 / DFS法
- 本题可约化为: 课程安排图是否是 有向无环图(DAG)。拓扑排序原理: 对 DAG 的顶点进行排序,使得对每一条有向边 (u, v),均有 u(在排序记录中)比 v 先出现。亦可理解为对某点 v 而言,只有当 v 的所有源点均出现了,v 才能出现。
- 通过课程前置条件列表 prerequisites 可以得到课程安排图的 邻接表 adjacency,以降低算法时间复杂度,以下两种方法都会用到邻接表。
方法一:入度表(广度优先遍历)
算法流程:
- 统计课程安排图中每个节点的入度,生成 入度表 indegrees。
- 借助一个队列 queue,将所有入度为 0 的节点入队。
- 当 queue 非空时,依次将队首节点出队,在课程安排图中删除此节点 pre:
- 并不是真正从邻接表中删除此节点 pre,而是将此节点对应所有邻接节点 cur 的入度 -1,即 indegrees[cur] -= 1。
- 当入度 -1后邻接节点 cur 的入度为 0,说明 cur 所有的前驱节点已经被 “删除”,此时将 cur 入队。
- 在每次 pre 出队时,执行 numCourses--;
- 若整个课程安排图是有向无环图(即可以安排),则所有节点一定都入队并出队过,即完成拓扑排序。换个角度说,若课程安排图中存在环,一定有节点的入度始终不为 0。
- 因此,拓扑排序出队次数等于课程个数,返回 numCourses == 0 判断课程是否可以成功安排。
复杂度分析:
- 时间复杂度 O(N + M): 遍历一个图需要访问所有节点和所有临边,N 和 M 分别为节点数量和临边数量;
- 空间复杂度 O(N + M): 为建立邻接表所需额外空间,adjacency 长度为 N ,并存储 M 条临边的数据。
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
indegrees = [0 for _ in range(numCourses)]
adjacency = [[] for _ in range(numCourses)]
queue = deque()
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre].append(cur) # 每门课需要先修的课程
for i in range(len(indegrees)): # 将所有入度为 0的节点入队
if not indegrees[i]: queue.append(i)
# BFS TopSort.
while queue: # 当 queue 非空时,依次将队首节点出队,在课程安排图中删除此节点 pre
pre = queue.popleft()
numCourses -= 1
for cur in adjacency[pre]: # 需要学习的课程
indegrees[cur] -= 1
if not indegrees[cur]: queue.append(cur) # 如果入度为0,重新入栈
return not numCourses方法二:通过 DFS 判断图中是否有环。
算法流程:
- 借助一个标志列表 flags,用于判断每个节点 i (课程)的状态:
- 未被 DFS 访问:i == 0;
- 已被其他节点启动的 DFS 访问:i == -1;
- 已被当前节点启动的 DFS 访问:i == 1。
- 对 numCourses 个节点依次执行 DFS,判断每个节点起步 DFS 是否存在环,若存在环直接返回 False。DFS 流程;
- 终止条件:
- 当 flag[i] == -1,说明当前访问节点已被其他节点启动的 DFS 访问,无需再重复搜索,直接返回 True。
- 当 flag[i] == 1,说明在本轮 DFS 搜索中节点 i 被第 2 次访问,即 课程安排图有环 ,直接返回 False。
- 将当前访问节点 i 对应 flag[i] 置 1,即标记其被本轮 DFS 访问过;
- 递归访问当前节点 i 的所有邻接节点 j,当发现环直接返回 False;
- 当前节点所有邻接节点已被遍历,并没有发现环,则将当前节点 flag 置为 -1并返回 True。
- 终止条件:
- 若整个图 DFS 结束并未发现环,返回 True。
复杂度分析:
- 时间复杂度 O(N + M): 遍历一个图需要访问所有节点和所有临边,N 和 M 分别为节点数量和临边数量;
- 空间复杂度 O(N + M): 为建立邻接表所需额外空间,adjacency 长度为 N,并存储 M 条临边的数据。
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
def dfs(i, adjacency, flags):
if flags[i] == -1: return True # 已被其他节点启动的 DFS 访问
if flags[i] == 1: return False # 已被当前节点启动的 DFS 访问,存在循环
flags[i] = 1 # 当前访问标志
for j in adjacency[i]: # 对逐门课的依次判断
if not dfs(j, adjacency, flags): return False
flags[i] = -1 # 设置访问完标志
return True
adjacency = [[] for _ in range(numCourses)] # 邻接矩阵,其index表示哪门课,值表示要先修哪些课程
flags = [0 for _ in range(numCourses)] # 所有课程访问的标志
for cur, pre in prerequisites:
adjacency[pre].append(cur) # 每门课需要先修的课程
for i in range(numCourses):
if not dfs(i, adjacency, flags): return False # 逐门课判断是否有循环
return True现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
示例 1:
输入: 2, [[1,0]] 输出: [0,1] 解释: 总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
在上一题的BFS基础上,添加几行用于保存课程即可。
from collections import deque
class Solution(object):
def findOrder(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: List[int]
"""
indegrees = [0 for _ in range(numCourses)] # 入度
adjacency = [[] for _ in range(numCourses)] #邻接矩阵
queue = deque()
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre].append(cur) # 每门课需要先修的课程
for i in range(len(indegrees)): # 将所有入度为 00 的节点入队
if not indegrees[i]: queue.append(i)
# BFS TopSort.
res = []
while queue: # 当 queue 非空时,依次将队首节点出队,在课程安排图中删除此节点 pre
pre = queue.popleft()
res.append(pre) # 保存课程
numCourses -= 1
for cur in adjacency[pre]: # 需要学习的课程
indegrees[cur] -= 1
if not indegrees[cur]: queue.append(cur) # 如果入度为0,重新入栈
# 拓扑排序出队次数等于课程个数(即numCourses == 0),返回排序,否则[]
return [] if numCourses else res这里有 n 门不同的在线课程,他们按从 1 到 n 编号。每一门课程有一定的持续上课时间(课程时间)t 以及关闭时间第 d 天。一门课要持续学习 t 天直到第 d 天时要完成,你将会从第 1 天开始。
给出 n 个在线课程用 (t, d) 对表示。你的任务是找出最多可以修几门课。
示例:
输入: [[100, 200], [200, 1300], [1000, 1250], [2000, 3200]] 输出: 3 解释: 这里一共有 4 门课程, 但是你最多可以修 3 门: 首先, 修第一门课时, 它要耗费 100 天,你会在第 100 天完成, 在第 101 天准备下门课。 第二, 修第三门课时, 它会耗费 1000 天,所以你将在第 1100 天的时候完成它, 以及在第 1101 天开始准备下门课程。 第三, 修第二门课时, 它会耗时 200 天,所以你将会在第 1300 天时完成它。 第四门课现在不能修,因为你将会在第 3300 天完成它,这已经超出了关闭日期。
1.每门课程的开始时间是没有要求的
2.按照deadline将课程从小到大排序
3.当前时刻能学这门课程的话,就学。如果学不了了,超过了deadline,必须扔一门课。那就扔耗时最长的那门课。time(当前时刻)可以回退
class Solution(object):
def scheduleCourse(self, courses):
"""
:type courses: List[List[int]]
:rtype: int
"""
courses.sort(key=lambda x:(x[1],x[0])) # #按照deadline排序
q , d = [] , 0
for c in courses:
d += c[0]
heapq.heappush(q,-c[0]) #将-c[0]压入堆q中
if d > c[1] : d += heapq.heappop(q) #选择的课程序列中,必须弹出一个。就弹那个耗时最长的(从堆中弹出最小的元素)
return len(q)描述
一个有n户人家的村庄,有m条路连接着。村里现在要修路,每条路都有一个代价,现在请你帮忙计算下,最少需要花费多少的代价,就能让这n户人家连接起来。
示例1
输入:
3,3,[[1,3,3],[1,2,1],[2,3,1]]返回值:
2
引入连通图来解决问题,n个村庄就是图上的n个顶点,然后,边表示两个村庄的路,每条边上的权重就是我们修建这条线路所需要的成本,所以现在我们有n个顶点的连通网可以建立不同的生成树,每一颗生成树都可以作为一个通信网,当我们构造这个连通网所花的成本最小时,搭建该连通网的生成树,就称为最小生成树。
由于最小生成树本身是一棵生成树,所以需要时刻满足以下两点:
- 生成树中任意顶点之间有且仅有一条通路,也就是说,生成树中不能存在回路;
- 对于具有 n 个顶点的连通网,其生成树中只能有 n-1 条边,这 n-1 条边连通着 n 个顶点。
连接 n 个顶点在不产生回路的情况下,只需要 n-1 条边。
所以克鲁斯卡尔算法的具体思路是:将所有边按照权值的大小进行升序排序,然后从小到大一一判断,条件为:如果这个边不会与之前选择的所有边组成回路,就可以作为最小生成树的一部分;反之,舍去。直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。筛选出来的边和所有的顶点构成此连通网的最小生成树。
判断是否会产生回路的方法为:在初始状态下给每个顶点赋予不同的标记,对于遍历过程的每条边,其都有两个顶点,判断这两个顶点的标记是否一致,如果一致,说明它们本身就处在一棵树中,如果继续连接就会产生回路;如果不一致,说明它们之间还没有任何关系,可以连接。
克鲁斯卡尔算法(Kruskal算法)
假设遍历到一条由顶点 A 和 B 构成的边,而顶点 A 和顶点 B 标记不同,此时不仅需要将顶点 A 的标记更新为顶点 B 的标记,还需要更改所有和顶点 A 标记相同的顶点的标记,全部改为顶点 B 的标记。
例如,使用克鲁斯卡尔算法找图 1 的最小生成树的过程为:
首先,在初始状态下,对各顶点赋予不同的标记(用颜色区别),如下图所示:
对所有边按照权值的大小进行排序,按照从小到大的顺序进行判断,首先是(1,3),由于顶点 1 和顶点 3 标记不同,所以可以构成生成树的一部分,遍历所有顶点,将与顶点 3 标记相同的全部更改为顶点 1 的标记,如(2)所示:
其次是(4,6)边,两顶点标记不同,所以可以构成生成树的一部分,更新所有顶点的标记为:
其次是(2,5)边,两顶点标记不同,可以构成生成树的一部分,更新所有顶点的标记为:
然后最小的是(3,6)边,两者标记不同,可以连接,遍历所有顶点,将与顶点 6 标记相同的所有顶点的标记更改为顶点 1 的标记:
继续选择权值最小的边,此时会发现,权值为 5 的边有 3 个,其中(1,4)和(3,4)各自两顶点的标记一样,如果连接会产生回路,所以舍去,而(2,3)标记不一样,可以选择,将所有与顶点 2 标记相同的顶点的标记全部改为同顶点 3 相同的标记:
当选取的边的数量相比与顶点的数量小 1 时,说明最小生成树已经生成。所以最终采用克鲁斯卡尔算法得到的最小生成树为(6)所示。
#
# 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
#
# 返回最小的花费代价使得这n户人家连接起来
# @param n int n户人家的村庄
# @param m int m条路
# @param cost int二维数组 一维3个参数,表示连接1个村庄到另外1个村庄的花费的代价
# @return int
#
class Solution:
def miniSpanningTree(self , n , m , cost ):
cost = sorted(cost, key=lambda x: x[2])
# tag 即为顶点的标记字典,可以通过顶点查询它的标记
tag = {vtx:vtx for vtx in range(1, n+1)}
res, num = [], 0
for u, v, w in cost:
# 在u, v未连接的情况下, 构建图
if tag[u] != tag[v]:
res.append([u, v, w])
tmp = tag[v]
# 将与v相连的定点,标记改为与u一样
for vtx in range(1, n+1):
if tag[vtx]==tmp:
tag[vtx]=tag[u]
num += w
# n个定点, n-1条边
if len(res) == n-1:
return num
return num684-冗余连接 (查并集)
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
示例 1:

输入: edges = [[1,2], [1,3], [2,3]] 输出: [2,3] 示例 2:

输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]] 输出: [1,4]
并查集
在一棵树中,边的数量比节点的数量少 11。如果一棵树有 NN 个节点,则这棵树有 N-1N−1 条边。这道题中的图在树的基础上多了一条附加的边,因此边的数量也是 NN。
树是一个连通且无环的无向图,在树中多了一条附加的边之后就会出现环,因此附加的边即为导致环出现的边。
可以通过并查集寻找附加的边。初始时,每个节点都属于不同的连通分量。遍历每一条边,判断这条边连接的两个顶点是否属于相同的连通分量。
-
如果两个顶点属于不同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间不连通,因此当前的边不会导致环出现,合并这两个顶点的连通分量。
-
如果两个顶点属于相同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间已经连通,因此当前的边导致环出现,为附加的边,将当前的边作为答案返回。
class Solution(object):
def findRedundantConnection(self, edges):
# pre为每个点对应祖先的集合
pre, res = list(range(len(edges)+1)), []
# 查找祖先
def find_root(r):
while pre[r] != r:
r = pre[r]
return r
# 合并树
for x, y in edges:
tx, ty = find_root(x), find_root(y)
# 找到最原始的父节点,如果不相等,即不构成环
if tx != ty:
pre[tx] = ty
else: # 构成环的边
res = [x, y]
return res在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
示例 1:

输入:edges = [[1,2],[1,3],[2,3]] 输出:[2,3] 示例 2:
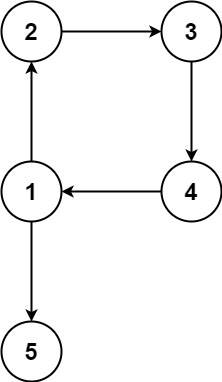
输入:edges = [[1,2],[2,3],[3,4],[4,1],[1,5]] 输出:[4,1]
基于上一题的思路,但是需要判断方向。当我们检测到环的时候,查看有没有入度为 2 的点:
- 如果没有,那么删除一条成环的边就可以,
- 如果有,我们先不把那个入度为 2 的点的那条边加入,形成环了,删除第一条边就可以
- 如果没有环就是没有连入根节点的情况,所以删除第二条边就可以
class Solution(object):
def findRedundantDirectedConnection(self, edges):
"""
pre:所有点的tag
res:入度为2的点
parent:保存有向点
last:构成环的边
"""
pre, res, parent, last = list(range(len(edges)+1)), [], {}, []
# 查找祖先
def find_root(r):
while pre[r] != r:
r = pre[r]
return r
# 合并树
for x, y in edges:
if y in parent: # 入度存在2
res.append([x, y])
res.append([parent[y], y])
else:
parent[y] = x
tx, ty = find_root(x), find_root(y)
# 找到最原始的父节点,如果不相等,即不构成环
if tx != ty:
pre[tx] = ty
else: # 构成环的边
last = [x, y]
if not res: return last # 没有入度为2的点, 删除构成环的
return res[1] if last else res[0] # 构成环, 删除后来入度的(第一个)描述
在一个有向无环图中,已知每条边长,求出1到n的最短路径,返回1到n的最短路径值。如果1无法到n,输出-1
示例1
输入:
5,5,[[1,2,2],[1,4,5],[2,3,3],[3,5,4],[4,5,5]]返回值:
9备注:
两个整数n和m,表示图的顶点数和边数。 一个二维数组,一维3个数据,表示顶点到另外一个顶点的边长度是多少 每条边的长度范围[0,1000]。 注意数据中可能有重边
动态规划:
dp[i+1] = min(dp[i]+cost, dp[i+1])
class Solution:
def findShortestPath(self , n , m , graph ):
# write code here
dp = [float('inf')]*n # 存储到各节点的距离
dp[0]=0 # 初始值
for i in range(n): # 遍历所有点
for j in range(m):# 遍历所有路径
if graph[j][0] == (i+1): # i+1是值从1开始
path = float('inf') if dp[i]== float('inf') else graph[j][2]+dp[i]
dp[graph[j][1]-1] = min(dp[graph[j][1]-1] ,path)
return dp[n-1]
#
class Solution:
def findShortestPath(self , n , m , graph ):
# write code here
dp=[float('inf')]*(n+1)
dp[1]=0
for i in range(2,n+1):
for j in range(m):
if graph[j][1]==i and dp[graph[j][0]]!=-1:
dp[i]=min(dp[i],dp[graph[j][0]]+graph[j][2])
if dp[i]==float('inf'):
dp[i]=-1
return dp[-1]有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市,则返回编号最大的城市。
注意,连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。
示例 1:

输入:n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4 输出:3 解释:城市分布图如上。 每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是: 城市 0 -> [城市 1, 城市 2] 城市 1 -> [城市 0, 城市 2, 城市 3] 城市 2 -> [城市 0, 城市 1, 城市 3] 城市 3 -> [城市 1, 城市 2] 城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市,但是我们必须返回城市 3,因为它的编号最大。
弗洛伊德算法
- 先定义一个邻接矩阵表示这个图,邻接矩阵所有值都初始化为阈值+1,然后根据边集edges先更新这个邻接矩阵;
- 用弗洛伊德算法计算图中各点之间的最短距离: (这一步的关键要点是要想明白点u到点v的最短距离d[u, v]得怎么更新,d[u, v] = min(d[u, v], d[u, k] + d[k, v]),其中k为图中所有的点)
- 用一个map存节点i的邻居中,距离小于阈值的个数;
- 返回这个map的最小value值对应的最后一个编号即可。
class Solution(object):
def findTheCity(self, n, edges, distanceThreshold):
"""
:type n: int
:type edges: List[List[int]]
:type distanceThreshold: int
:rtype: int
"""
dp = [[distanceThreshold+1]*n for _ in range(n)]
for i in range(n): dp[i][i]=0
for u, v, w in edges:
dp[u][v] = w
dp[v][u] = w
for k in range(n):
for i in range(n):
for j in range(n):
dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j])
res, count = 0, n+1
for i in range(n):
cur = 0
for j in range(n):
if dp[i][j] <= distanceThreshold:
cur += 1
if cur <= count:
res, count = i, cur
return res