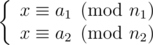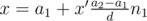Prepared reference link
https://hackmd.io/YZDNajrWTc2YXvySPKQQlA?view
Lambda (C++11 stuff)
Function in Function
auto function = [](auto x){
return ...;
};Boolean Comporator
sort(q, q + n, [&](int A, int B) { return A < B; });Tricks
-
Sum-Xor property
-
Any even number greater than 2 can be split into two prime numbers
-
Pragmas
#pragma GCC optimize ("O3")
#pragma GCC optimize ("unroll-loops")
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,fma")
-
find all B that B is submask of A
(B = A; B > 0; --B, B&=A); -
find all D that A is submask of D
for (D = A; D < (1 << n); ++D, D |= A) -
Rotate board 45 degree by (x,y) -> (x+y,y-x), so Manhattan distance between two points would be max(|x1-x2|,|y1-y2|)
-
Find any x,y such that ax+by=gcd(a,b) for given two integers a and b with EEA(Extended Euclidean Algorithm )
int gcd(int a, int b, int& x, int& y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
int x1, y1;
int d = gcd(b, a % b, x1, y1);
x = y1;
y = x1 - y1 * (a / b);
return d;
}
-
There is no assumption that n1 and n2 are coprime. Find an integer x that satisfies:
Answer:, where d=gcd(n1,n2) and x' from EEA we can find (x', y') such that n1x' + n2y' = d
-
-
, so it applies for multiple arguments
-
For some permutation
with length
the absolute differences of adjacent values equal to sum of numbers between positions of
and
for each
.
More formally:
