KimferLang/hmm_for_autonomous_driving

Educational application of Hidden Markov Model to Autonomous Driving

hmm_for_autonomous_driving

WORK IN PROGRESS!!

Introduction

Disclaimer:

• The goal of this repository is to get more familiar with the concepts of Hidden Markov Models (= HMM).
• The scope of ambition is therefore limited and the examples are very simple, only serving educational purposes.

Addressed topics:

• Problem setting using a basic example to introduce the HMM terminology.
• Illustration of the Bayes Rule to determine the most likely sequence of state given a observation sequence.
• Implementation of the Forward and Backward Algorithm to compute the probability of a particular observation sequence.
• Implementation of the Viterbi Algorithm to find the most likely sequence of hidden states which could have generated a given observation sequence (posterior decoding).
• Implementation of the Baum-Welch Algorithm to find the most likely parameters (state transition and emmission models) of the HMM given a observation sequence (parameter learning task).

?? Given the model parameters, : is Solved by the Viterbi algorithm and Posterior decoding.

?? Structure:

• Problem motivation
• ...

Problem motivation

For left-hand-drive countries such as the UK, just invert the reasoning 😃

• Your car is driving on a 2-lane highway.
• Imagine that you can remotely monitor the velocity of the car (I communicate it to you)
• But you do have no direct access to the lateral position (right lane of left lane). Formally, you cannot view the underlying stochastic walk between lane states.
• How could you deduce the lane based on the single information we receive (the speed)?

Emission probability

If I am telling you that I am driving with a low speed, you may deduce that I am on the right lane.

• For instance, because I am just driving alone at a reasonable pace
• Or because I am blocked by a slow vehicle.
• But I could also drive fast on this right lane (have you ever been driving alone on a German highway?)

Similarly, if you get informed of a high speed, you could say that I am more likely to be driving on the left lane.

• Probably overtaking another vehicle.
• Nevertheless, this is not always true: think of the situation where you are waiting on the left lane behind a truck trying to overtake another truck.

We get a first intuition:

• The variable lane seems to have an impact on the variable speed.
• In other words: you do not drive at the same pace depending if you are one the left lane or the right lane.
• But the relation is not deterministic, rather stochastic.

This finding will be modelled using emission probabilities in the following.

Transition probability

You could have another intuition:

• Human drivers usually stay on their lanes.
• Hence if you are on right lane at time t, you are likely to still be on right lane at time t+1.
• Again, this does not always hold and you can find exception.
• But here comes a second intuition: the lane at time t is influenced by the lane at time t-1.

The concept of transition probability will be used to model this second remark.

Terminology

The speed is the observation while the lane constitutes the hidden state. Some examples show that all emissions are possible

Objectives

We can now define three problems which can be solved by an HMM:

• 1- Learning

  • The first is learning the parameters of its the latent structure (emission, transition and initial state models).
  • In the case of a known structure and some fully observable sampling, on can apply the concept of Maximum Likelihood Estimation (MLE):
    • Some observation sequences (speed) and their associated states (lane) have been collected. The samples form the training dataset.
    • The parameter can be selected so as to maximise the likelihood for the model to have produced the data from the given dataset.
  • In case it is not possible to sample from hidden states (partially observable), one can use Expectation Maximization (EM) or Markov Chain Monte Carlo (MCMC)
  • Learning is covered in questions Q1 and Q5

• 2- Evaluation

  • The second task is to find, given a HMM, how likely is it to get a observation sequence.
  • It is covered in question Q3

• 3- Inference

  • The third one is applying the trained HMM to an observation sequence. We want to find the sequence of states that best explains the observation sequence.
  • Concretly we want to infer the sequence of lanes driven by the car ((right or left) = hidden state) based on a sequence of speed measurements (= observation).
  • In this case, you can thing of HMM as a sequence classifier (if we make the hidden state of HMM fixed, it would have been a Naive Bayes classifier).
  • Inference is covered in questions Q2 and Q4
  • Three types of inference can be distinguished:
    • Filtering: determine the latest belief state, i.e. the posterior distribution P(lane(t) given [speed(1), ..., speed(t)])
    • Decoding: determine the hidden state sequence, that gives the best explanation for the observation sequence
      • find [lane(1), ..., lane(t)] that maximizes P([lane(1), ..., lane(t)] given [speed(1), ..., speed(t)])
      • it is equivalent to maximizing the Joint Probability P([lane(1), ..., lane(t)] given [speed(1), ..., speed(t)]) since the marginal over observation is independant of the variables we are maximizing over.
    • Prediction: determine the probability for the future hidden state in K steps, i.e. the posterior conditional distribution P(lane(t+K) given [speed(1), ..., speed(t)] )
    • Smooting: determine the probability for the past hidden state K steps ago, i.e. the posterior conditional distribution P(lane(t-K) given [speed(1), ..., speed(t)] )

Assumptions

To keep the problem as simple as possible:

• Let's discretize the speed into low speed and high speed.
• Time steps are discretized.
• Lane transitions are ignored: either you are on left lane or you are on right lane.

Stationary Process

• We assume that the HMM models (transition and emission matrices and initial distribution) are constant over time
• P[speed(t) given lane(t)], P[lane(t+1) given lane(t)] and P[lane(t)] are independant of t.

Observation Independence

• We talked about emission probability, explaining that state lane (t) impacts observation speed (t).
• One could other sources of influence: speed (t-1) and lane (t-1) for instance.
• Here we assume that the probability of an observation depends only on the state that produced the observation and not on any other states or any other observations
• Each observation variable speed depends only on the current state lane.
• This is a strong assumption since we decide not to capture dependencies between each input element in the observation sequence
• But it will relax computation during decoding.
• In supervised learning terminology: "each feature (observation) is conditional independent of every other feature, given the class (hidden state)"
• As for Naive Bayes, probabilities are independent given the class y and hence can be "naively" multiplied: p(x1,x2,…,x1|y)=p(x1|y) * p(x2|y) * ... * p(xm|y)

First-order Markov Property

• We just said that it is useful to know the present lane (at time t) to infer the future lane (at time t+1).
• What about the previous lane at t-1? It probably also hold relevant information?
• Here is a strong assumption about inferring in this stochastic process:
  • the conditional probability distribution of future states of the process (conditional on both past and present states) depends only upon the present state, not on the sequence of events that preceded it.
• In other words, "the future is independant of the past given the present".
• This strong assumption is known as the first-order Markov Property (also named "memoryless property") and will make computations easier in the following.

Based on these assumptions, the problem can be modelled using a graphical model:

• The Markov Property makes sure state connection occurs only for consecutive states.
• The Output Independence is responsible for each observation to receive only a single edge (coming from the associated state).
• HMM are directed models (hence arrows) since we can distinguish what is the reason (lane state) and what is the result (speed observation).
• HMM is a special case of Dynamic Bayesian Network (Dynamic belief network) since it forms a probabilistic directed acyclic graphical model.

HMM Graphical Representation

Relations with other machine learning techniques

For better understanding, I find convenient to compare HMMs with the other algorithms and methods I know.

• HMM is a special case of Finite State Machine (FSM).

• Kalman Filters can be conceived of as continuous valued HMMs.

• HMM is a special case of Dynamic Bayes Networks (DBNs) in which the entire state of the world is represented by a single hidden state variable.

• HMM and Partially Observable Markov Decision Processes (POMDPs) have many similarities in their formulations. But in POMDPs, the user has some control (not just a spectator) over the process transitions between hidden states (introduction of the concept of action).

• Contrary to HMM, in Naive Bayes model, hidden state are fixed (no state sequence since there is no transition happening).

• States are hidden in HMM. They are fully observable in Markov Chains.

• HMM is a special case of Generative Directed Graphs (GDG), where the graphical structure is a first-order-chain structure (one could impose dependencies to arbitrary elements, not just on the previous element).

• Linear-Chain CRF can be seed as the discriminative version of HMM (like Logistic Regression and more generally Maximum Entropy Models are the discriminate version of Naive Bayes) i.e. the consideration is on the conditional probability p(y|x) instead of the joint probability p(y,x).

• In Conditional Random Fields (CRF), the two strong (unreasonable) HMM hypotheses are dropped (it better addresses the so-called "labeling bias issue" but also become more complicated for inference).

• Maximum Entropy Markov Models combine features of HMMs (Markov chain connections) and maximum entropy (MaxEnt) models: it is a discriminative (not generative) model that allows the user to specify lots of correlated, but informative features.

  • MEMMs focus on p（state|observation), while HMMs focus on p（observation|state）
  • btw, CRF can be seen as a more advanced MEMM with global variance normalization and with undirected connections, to address the issue of "label bias problem"
  • HMM models "state decides observation" and this is why it is called "generative". MEMMs model "observation decides state".

HMMs share concepts with other methods and algorithms

Problem formulation

Definitions:

A Hidden Markov Model (HMM) is a 5-tuple composed of:

• A set of Hidden States: discrete random variable lane in {Right Lane, Left Lane}
• A set of possible Observations: discrete random variable speed in {Low Speed, High Speed}
• A stochastic matrix which gives Emission probabilities: P[speed(t) given lane(t)]
• A stochastic matrix which gives Transition probabilities: P[lane(t+1) given lane(t)]
• A Initial State Probability distribution: P[lane(t=t0)]

Questions:

• Q1 - How to derive our probability models?
• Q2 - If you receive a single speed observation, what is the probability for the car to be in each lane?
• Q3 - What is the probability to observe a particular sequence of speed measurements? For instance [low speed, high speed, low speed].
• Q32 - Given a sequence of speed measurements, what is the most likely latest lane?
• Q4 - What is the most likely lane sequence if the observation sequence is [low speed, high speed, low speed]?
• Q5 - What if you are not directly given the probability models?

Answers

Q1 - How to derive our probability models?

Given some observation speed sequence and the associated lane states

• Here are only a few for simplicity but you could imagine longer recordings.
• You can think of it as some samples of the underlying joint distributions.
• How can we estimate the HMM parameters (for the emission, transition and intial state models)?
• We can count how many times each event occurs in the data and normalize the counts to form proper probability distributions.
• In can be formalize with Maximum Likelihood Estimation in the context of Supervised Learning.

The idea is to approximate the model parameters by counting the occurrences, similar to Naive Baye method where training is mainly done by counting features and classes.

Transition probability

Counting the number of transitions, we can derive a transition probability model.

• For instance, among the 15 transitions starting from right lane, 3 ended in left lane.
  • Hence P[right lane -> left lane] = 0.2
• Since probabilities must sum to one (normalization), or just by counting for the other case (right lane is followed 12 times by a right lane)
  • Hence P[right lane -> right lane] = 0.8

Derivation of the transition probability model

Emission probability

Counting can also be used to determine the emission probability model.

• Similar to Naive Bayes in Supervised Learning where we count occurrences of features for all classes in the training data.
• For instance, how many times has the hidden state left lane caused a high speed observation?

Derivation of the emission probability model

Initial state probability

At any time t, what is your guess on the distribution of the hidden state if no observation is given?

• Two options are available:
  • Either you use the transition model (1) and the fact that probabilities sum to 1 (2):
    • (1) P[left lane, t] = P[left lane -> left lane] * P[left lane, t-1] + P[right lane -> left lane] * P[right lane, t-1]
    • (2) P[right lane, t] = 1 - P[left lane, t]
  • Either you simply count occurrences in the supplied data. We simple count how many samples in the training data fall into each class (here state instance) divided by the total number of samples:
    • P[left lane, t] = 1/3
    • P[right lane, t] = 2/3

Note: incomplete or missing state/observation

How to cope with absence of one state or one observation instance in the sampled data?

• Obviously we would need to collect much more pairs to refine the parameter estimation of our models.
• Clearly, assigning 0 may cause issues in the inference process.
• Every state could have a small emission probability of producing an unseen observation
  • P(obs | state) = espilon_for_unseen_case if obs has not been seen.
• Look for "Laplace Smoothing" or "Additive Smoothing" if you are interested.

Summary

Hidden Markov Model with the initial state probability model (up), transition probability model (middle), and the emission probability model (below)

Q2 - If you receive a single speed observation, what is the probability for the car to be in each lane?

Prior

Before any observation we know that right lane appears 2/3 of the time and left lane 1/3.

• These probabilities would have been the answers if we were to ignore the observation.
• This distribution (called prior) must be updated when considering the observation.
• When considering the observation, the prior is converted to a posterior using likelihood terms.

Likelihood

Based on supplied data, we found that on the left lane it is more likely to drive fast. And slow on the right lane. In other words, you will be rather "suprised" if a left lane causes. I like the concept of "Surprise" to introduce the concept of "Likelihood"

• The likelihood is, in this case, equivalent to the emission probability:
  • given a state, what is the probability for each observation.
• Actually, the question is interested by the exact opposite:
  • given an observation, what is the probability for each state?
  • this is called the posterior and is linked to prior via the likelihood.

Marginal

The Bayes Rule states that Posterior = Normalized (prior * likelihood)

• The normalization (the posterior terms must sum to 1) is achieved using the Marginal Probabilities.
• Under all possible hypotheses, how probable is each speed?
• Using the law of total probability:
  • P(high speed) = P(high speed given left lane) * P(left lane) + P(high speed given right lane) * P(right lane)
  • P(low speed) = P(low speed given left lane) * P(left lane) + P(low speed given right lane) * P(right lane)
• Eventually:
  • P(high speed) = 1/3
  • P(low speed) = 2/3

Bayes Rule

• Let's use Bayesian Statistics to recap:
  • P(lane given speed) = P(lane) * P(speed given lane) / P(speed)
  • Posterior = Prior * Likelihood / Marginal
• For instance
  • P(left lane given high speed) = P(left lane) * P(high speed given left lane) / P(high speed)

Priors:

• P(right lane) = 2/3
• P(left lane) = 1/3

Marginals:

• P(high speed) = 1/3
• P(low speed) = 2/3

Likelihoods:

• P(high speed given left lane) = 0.6
• P(low speed given left lane) = 0.4
• P(high speed given right lane) = 0.2
• P(low speed given right lane) = 0.8

Posteriors:

• P(left lane given high speed) = 1/3 * 0.6 / 1/3 = 0.6
• P(left lane given low speed) = 1/3 * 0.4 / 2/3 = 0.2
• P(right lane given high speed) = 2/3 * 0.2 / 1/3 = 0.4
• P(right lane given low speed) = 2/3 * 0.8 / 2/3 = 0.8

Summary

Derivation of the posterior probabilities for a single observation

The question was given an observation, what is the most likely hidden state?. Well, just looking at the numbers on the figure below and taking the max(), the answer is:

• Given high speed is observed, the most likely state is left lane
• Given low speed is observed, the most likely state is right lane

It is close to our intuition.

This method is sometimes named "Posterior Decoding".

Q3 - What is the probability to observe a particular sequence of speed measurements?

Had it been a first-order Markov Chain (no hidden state), one could have marginalized over all speed(t) observations and simplify the large expression using the conditional independance offered by the Markov Property.

The final expression would be:

• P([speed(1), ..., speed(t)]) = P[speed(1)] * SUM ( P([speed(t) given speed(t-1)]) )

In the HMM case, we need to add some modifications:

• We use the transition model to navigate between two states.
• We use the emission model to generate each observation.

Derivation of the probability of an observation sequence

This requires to develop all the possible state sequences of size T.

• In our case state space has size 2 (left_lane, right_lane). Hence the sum will contain 2^T terms.
• This naive (meaning we list all the possibilities based on the definition of marginal probabilities) approach can nevertheless become impractible for larger state spaces and/or large sequence sizes.

An alternative is to use Dynamic Programming.

• the idea is to compute cells in a table alpha(i, t)
  • think of rows (index i) as state instances (left_lane, right_lane)
  • think of columns (index t) as time step (t=1, t=2, ... , t=T)
• three notable relations:
  • 1st relation: alpha(i, t+1) can be computed from alpha(i, t).
    • Hence we can the table can be filled efficiently (only 2T terms in the table)
    • Idea of the derivation:
      • marginalize alpha(i, t+1) over state(t)
      • split observation[1 ... t+1] = observation[1 ... t] + observation(t+1)
      • decompose the joint probability into a product of conditional probabilities (isolate observation(t+1) and state(t+1))
      • use conditional independance to simplify two terms ([given state(t), state(t+1) is independant of all possible observation] and [given state(t+1), observation(t+1) is independant of all other terms])
      • three terms are left: [emission at t+1], [transition from t to t+1] and [alpha(i, t)]
      • alpha(i, t+1) = [emission at t+1] * SUM[over state(t)] [transitionttot+1 * alpha(i, t)]
  • 2nd relation: the table initialisation [alpha(i, t=1)] is easily computed with the initial state distribution and the emission model.
  • 3rd relation: the marginal probability (what we are really looking for) can be expressed with the alpha(i, T) (just by summing the terms of the last column).
  • Therefore it is computationally-efficient to fill the alpha table to derive the marginal distribution of observation sequence.

Derivation of construction rules for the alpha table

Each element in the column t+1 is a weighted sum of the elements at t:

• The weights are the transition probabilities
• The obtained sum is finally scaled by the emission probability (for the state i to emit the observation present at t+1 in our observation sequence)

Construction of the alpha table using Dynamic Programming

Once the alpha table is constructed, it is straight forward to get the the marginal probability for the associated observation sequence:

• summing the alpha values at time t gives the probabily of the observation sequence up to time t
• for instance, among the 8 possible 3-observable sequences, [low speed, high speed, low speed] has a probability = 0.13184

Use of the alpha table for the marginal probability of an observation sequence

Q32 - Given a sequence of speed measurements, what is the most likely latest lane?

Filtering is one important application for robotics and autonomous driving:

• We often want to estimate the current state of some objects (e.g. position, speed, or a belief over the route intention).
• In order to reduce the variance of the estimate, you may want not to base your estimation only on the latest measurement.
• Hence, similar to what is done with Bayesian Filters (BFs) (such as Kalman Filters, Particles Filters), two ingredients are used to update your latest State Belief:
  • a sequence of measurements (= observation)
  • some evolution models
    • for instance odometry measurements and constant acceleration or constant velocity models in the context of sensor fusion for localization
    • here we have an emission model and a transition model)

The form of the alpha table turns out to be very appropriate for filtering:

• Let's focus on P(lane(t=3) == right given [low speed, high speed, low speed])
• Express condition probability with the joint probability.
• Note that we find the marginal probability of the observation sequence at the denominator.
• Marginalize it over last the hidden state lane(t=3).
• All terms left are alpha values.

Use of the alpha table for filtering

Note: Markov Property

Why do you consider all the three observations? Does not the Markov Property state that you only need the latest one?

Have a look at the graphical representation of the HMM.

• The Markov Property only applies for the transitions between hidden states.
• The rule of D-separation (commonly used in Bayesian Networks) states that the knowledge of the realisation of one previous hidden could have blocked the path from some observations.
• That would have made our result conditionally independant of these observations.
• For instance, in P(lane(t=3) == right given [low speed, high speed, low speed] and lane(t=1)==right), the first observation (at t=1) is useless since all its paths to lane(t=3) (there is only one path here) are blocked by lane(t=1) (which realisation is known).
• Since we only consider realisations of observation, no simplification can be done.

Actually, when filtering over the last observation only, we get a different result:

• P(lane(t=3) == right given [low speed, high speed, low speed]) = 0.73786
• P(lane(t=1) == right given [low speed]) = 0.8 (also readable in the alpha table: 8/10 / (8/10 + 2/10) )

From alpha table to beta table

The alpha table can be used:

• To determine the belief state (filtering).
• To compute marginal probability of an observation sequence.

Note that the alpha table was completed starting from left and moving to right

• This is the reason why this inference method is called "Forward Algorithm"
• One could have the idea of going the other way round.
• This would lead to the beta table

Derivation of construction rules for the beta table

Construction of the beta table using Dynamic Programming

The beta table can actually be used to compute the marginal probability of an observation sequence:

• Let's focus on P([low speed, high speed, low speed])
• Marginalize over the first hidden state lane(t=1) (insert it in the joint distribution and sum over all its possible realisations)
• Write the decomposition specific to the HMM structure (an first-order Markov Chain).
• The term P(speed[2 ... t] given lane(1)==j) is by definition beta(j, t=1)
• In other words, the marginal probability of an observation sequence can be obtained from the terms in the first columns of the associated beta table.

Use of the beta table for the marginal probability of an observation sequence

Smoothing

Smooting is made easy when alpha table and beta table have been computed for an observation sequence.

• Let's consider the observation sequence [low speed (t=1), high speed (t=2), low speed (t=3)]
• What is the probability distribution for the lane at t=2?
• Note that we can answer the question for t=3: cf. filtering of Q32.

Ideas for the derivation: - the posterior probability is turned to a joint probability over all possible hidden states, introducing a normalization constant - P(lane(t=2) == left given [low speed (t=1), high speed (t=2), low speed (t=3)]) - the observation sequence is split at t=2 - = P(lane(t=2) == left and [low speed (t=1)] and [high speed (t=2), low speed (t=3)]) / Normalization_constant - = P(lane(t=2) == left and [low speed (t=1)]) * P(lane(t=2) == left given [high speed (t=2), low speed (t=3)]) / Normalization_constant - Note that [low speed (t=1)] does not appear in the second term (conditional probability), since given the realisation of lane(t=2), all its paths to [high speed (t=2), low speed (t=3)] are "blocked" (conditional independance). - = alpha (left, t=2) * beta(left, t=2) / Normalization_constant

• Since probabilities must sum to one,
  • Normalization_constant = alpha(left, t=2) * beta(left, t=2) + alpha(right, t=2) * beta(right, t=2)
  • Normalization_constant = 14/125 * 0.56 + 12/125 * 0.72 = 0.13184
  • This result should be familiar to you ;-)
• For each time t, [SUM over lane i of (alpha(i, t) * beta(i, t))] represents the probability of observing [low speed, high speed, low speed] among the among the 8 possible 3-observable sequences
  • For t=1: (2/15) * 0.2592 + (8/15) * 0.1824 = 0.13184
  • For t=2: (14/125) * 0.56 + (12/125) * 0.72 = 0.13184
  • For t=3: (108/3125) * 1 + (304/3125) * 1 = 0.13184
• Answers:
  • P(lane(t=2) == left given [low speed (t=1), high speed (t=2), low speed (t=3)]) = (14/125) * 0.56 / 0.13184 = 0.475728
  • P(lane(t=2) == right given [low speed (t=1), high speed (t=2), low speed (t=3)]) = (12/125) * 0.72 / 0.13184 = 0.524272
  • ??? Very close result between the two instances of lane.

Prediction

Given an observation sequence, distributions over future hidden states can be inferred using a variant of the alpha table.

• Let's consider the observation sequence [low speed (t=1), high speed (t=2), low speed (t=3)]
• What is the probability distribution for the lane at t=5, i.e. in two time steps in the future?
• Note that we can answer the question for t=3: cf. filtering of Q32.
• Using Dynamic Programming, we define a new quantity pi such as
  • pi(lane i, time t+k) = P(lane (t+k) = i given [speed(1) ... speed(t)])

A recursion rule can be derived:

• pi(lane i, time t+k+1) = SUM over state j of [P(lane(t+k+1)=i given lane(t+k)=j) * pi(lane i, time k+1)]
  • For the derivation, insert lane(t+k)=j in the definition of pi(lane i, time t+k+1).
  • Since its realisation is not known, we marginalize over lane(t+k)=j.
  • Break the joint part [lane(t+k+1)=i and lane(t+k)=j] in a conditional.
  • The expression can be simplified since lane(t+k+1)=i is conditionally independant of the observation sequence (lane(t+k)=j is blocking )

The initialisation has k=0, i.e. it is a filtering problem (inference for the current time):

• similar to the computation in Q32,
• pi(i,0) = pi(lane i, time t+0) = P(lane(t) = i given [speed(1) ... speed(t)]) = alpha(i, t) / [SUM over j of alpha(j, t)]

In other words,

• Each element of the last columm of the alpha table is used to initialize the first column in the pi table.
• Then each element in the pi table is a weighted sum of the elements in the previous column.
• Weights are the transition probabilities.

Derivation of construction rules for the pi table using Dynamic Programming

Construction of the pi table using Dynamic Programming

Use of the pi table for prediction

Answer:

• P(lane = right at t=5 given [low speed (t=1), high speed (t=2), low speed (t=3)]) = pi(right lane, k=2) = 0.688
• P(lane = left at t=5 given [low speed (t=1), high speed (t=2), low speed (t=3)]) = pi(left lane, k=2) = 0.312

Is there a convergence of the pi values as k grows?

• Intuitively, it is asking the question: what will be the hidden state in an infinite number of steps?
• It converges to the initial state distribution
• It forgets about the observation and conditional probability becomes a prior probability

pi_table.ipynb computes the pi(k) values associated to this observation sequence for any time step t+k.

import numpy as np
# 0 = left
# 1 = right
pi_zero = np.array([0.8, 0.2])  # deduced from the `alpha_table`
transition = np.array([[0.8, 0.4], [0.2, 0.6]])

def pi(k):
    if k == 0:
        return pi_zero
    return np.dot(transition, pi(k-1))

k	pi(right lane, k)	pi(left lane, k)
0	0.8	0.2
1	0.72	0.28
2	0.688	0.312
3	0.6752	0.3248
4	0.67008	0.32992
5	668032	0.331968
10	66668065	0.33331935
inf	2/3	1/3

Change in the state distribution as the prediction horizon increases

Remark:

• The pi table can also be used to make predictions about the observation.

Q4 - What is the most likely lane sequence if the observation sequence is [low speed, high speed, low speed]?

Question interpretation

When trying to reformulate the question, I was puzzled since I ended up with two possible answers.

It all depends on what we mean with "What is the most likely state sequence given an observation sequence?"

• it can be the state sequence that has the highest conditional probability? This is was we have done in Q2 with #BayesRule. #PosteriorDecoding.
• it can be the state sequence that makes the observation sequence the most likely to happen? #MLE. #Viterbi. In this case, we compute the Joint Probabilities i.e. the probabilities for the Intersection [State Sequence + Observation Sequence].
• ??(can the MLE be on the conditional probability of observation given state? what differs with the upper joint event is the normalization)??
• ?? argmax(A)(P[A, B]) = argmax(A)(P[A| B])

In other words, the answer could be maximizing two kind of probability

• either the conditional probability: (state given observation)
• or the joint probability: (state and observation).

For this question, we will be looking for the most likely sequence of hidden states which could have generated a given observation sequence.

Maximum Likelihood Estimation (MLE)

We will to pick the sequence (in Q2 it was of size 1) of hidden states that makes the observations the most likely to happen.

This method is called Maximum Likelihood Estimation (MLE).

Derivation of the probability of the event [RL-LL-RL; LS-HS-LS]

Here are the different steps performed for the observation sequence [low speed, high speed, low speed].

• First enumerate the 2^3 = 8 possible sequences of hidden states.
• For each candidate, compute the probability for the state sequence candidate to generate the observation sequence.
  • Start by the probability of the first state element to happen (initial state probability).
  • List the emission and transition probabilities.
  • The probability of the observation sequence (?likelihood) is the product of all listed probabilities (thank @MarkovProperty).
• Apply max() to get the Maximum Likelihood Estimate:
  • In this case, the state sequence [right lane, right lane, right lane] makes the observation sequence the most likely to happen.

Our three assumptions (First-order Markov property, Observation Independance and Stationary Process) simplify the computation of the joint distribution of sequences

For instance with the state sequence candidate [low speed, high speed, low speed]

• The joint probability is the product of all the probabilities listed on the figure below.
• P([low speed, high speed, low speed] and [right lane, left lane, right lane]) = 0.02048

Derivation of the MLE for a particular observation sequence

Note

0.1318394 = 0.01152 + 0.01536 + 0.000853 + 0.01536 + 0.054613 + 0.0068267 + 0.02048 + 0.0068267

If you sum all the probabilities of the eight cases depicted the figure above, you do not end up to 1, but to 0.1318394. Why?

• Well, 0.1318394 represents the probability for the observation sequence [low speed, high speed, low speed] to happen.
  • P[low speed, high speed, low speed] = P[obs] = P[obs && state seq1] + P[obs && state seq2] + ... + P[obs && state seq8]
  • ?? total probability is with conditional. What is it with intersections?
  • We had already find this result in Q3
• What would sum to 1 is the sum over all possible 3-element observation sequences:
  • 1 = P[LLL] + P[LLH] + P[LHL] + P[LHH] + P[HLL] + P[HLH] + P[HHL] + P[HHH]

The presented approach could be used for larger observation sequences. By the way you notice that HMM can handle inputs of variable length. But for longer observation sequences, an issue appears:

Size of the observation sequence	Number of probabilities to compute before applying max() (for MLE)
1	2
2	4
3	8
i	2^i
10	1024

Dynamic Programming: an alternative to the naive enumeration

Assume that after the second observation, the sub-sequence (left lane, right lane) is found to be more likely that the sub-sequence (right lane, right lane).

• Is it worth carry on some investigation in the branch (left lane, right lane)?
• Do not forget that the only goal is to find the most likely sequence (and nothing else)!
• Whatever you append to the sub-sequence (left lane, right lane), the resulting sequence will be less likely than appending the same to (right lane, right lane).

This example show the intuition of Dynamic Programming:

Compute local blocks and consider only the most promising ones to build the next ones.

Dynamic Programming is nothing but cached recursion

To better understand the concept of Dynamic Programming and its benefits, cached_vs_vanilla_recursion.ipynb compares the performance of two recursive approches on the famous Fibonacci computation.

The first one implements "classic recursion":

def fibo_vanilla_recursive(i):
    if i <= 0:
        return 0
    elif i == 1:
        return 1
    else:
        return fibo_vanilla_recursive(i-1) + fibo_vanilla_recursive(i-2)

%timeit for _ in range(10): fibo_vanilla_recursive(10)

237 µs ± 14.3 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

In the second one reuses previous results in the computation, i.e. a "cached recursion":

cache = {0:0, 1:1}
def fibo_cached_recursive(i):
    if cache.get(i) is not None:
        return cache[i]
    else:
        res = fibo_cached_recursive(i-1) + fibo_cached_recursive(i-2)
        cache[i] = res
        return res

%timeit for _ in range(10): fibo_cached_recursive(10)

2.33 µs ± 140 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

The difference in the computational time is substantial (all the more since it only goes to 10!).

Let's count how many times each fibo_vanilla_recursive(i) is called when computing all fibo_vanilla_recursive(k) for k in range(10).

Repetition in computation with the vanilla Fibonacci recursion

Viterbi algorithm: similar to the (alpha) Forward Algorithm, with MAX() instead of SUM()

This is a maximization problem:

• The goal is to find the hidden state sequence [lane_t=1, lane_t=2, lane_t=3] that maximizes the joint probability P([lane_t=1, lane_t=2, lane_t=3] and [low speed (t=1), high speed (t=2), low speed (t=3)])

Let's call L\* the optimal hidden state sequence, and let's note L1 = lane_t=1, L2 = lane_t=2 and L3 = lane_t=3:

• L* = argmax_over_L1_L2_L3(P([L1, L2, L3] and [low speed (t=1), high speed (t=2), low speed (t=3)]))
• This joint probability can be turned to a sum of conditionnal probabilities:
• L* = argmax_over_L1_L2_L3(term_1 * term_2 * term_3)
• L* = argmax_over_L3(argmax_over_L2(argmax_over_L1(term_1 * term_2 * term_3)))
• With (simplified using the conditional independance of the HMM structure):
• term_1 = P(L1) * P(low speed (t=1) given L1) * (P(L2 given L1)
• term_2 = P(high speed (t=2) given L2]) * (P(L3 given L2])
• term_3 = P(low speed (t=3) given L3])
• Maximizing over [L1, L2, L3] is equivalent to maximizing over [L1] over [L2] over [L3]
• Therefore let's group the terms that depend on what is maximized:
• L* = argmax_over_L3(term_3 * argmax_over_L2(term_2 * argmax_over_L1(term_1)))
• Now, we can start from the right side, solving the maximization over L1 (it does not depend of L2)
• Then store this result in memory and use it to solve the maximization over L2
• Finally use the retult to solve the maximization over L3
• This is the idea of the Dynamic Programming approach.

Similar to the alpha, beta and pi variables, let's introduce alpha\*(i, t):

• alpha*(i, t) = P([observed speed (t=1), ..., observed speed (t=t)] and [L1, ..., Lt-1] being optimal and lane_t = i)
• It can be noted that alpha\*(i, t) is very similar to alpha(i, t):
  • Except that alpha(i, t) does not have the term "and [L1, ... Lt-1] being optimal"
  • Instead, alpha(i, t) was marginalizing over [L1, ... Lt-1]
  • Here, alpha\*(i, t), their value are fixed to the optimal sub-sequence for the time [1, t-1]
• A recursion rule can be establish:
  • "[L1, ..., Lt] being optimal" can be written
    • max_over_j("[L1, ..., Lt-1] being optimal and Lt = j")
    • And the value that maximizes this quantity is precisely the optimal value of Lt\* (i.e. ** the t-th element in L\***)
  • Then decompose the joint probability into some conditional probability
  • Simplify the expression using the conditional independance:
  • It yields to:
    • alpha*(i, t+1) = P(speed_t+1 given Lt+1=i]) * P(Lt+1 given Lt]) * max_over_j[alpha*(j, t)]
  • This is very similar to the alpha construction, except that the elements at t+1 are constructed using the max() over elements at t instead of summing all elements at t.
  • It is important, when solving the max(), to store the argmax(), i.e. the lane that has the higest alpha\*.
    • This information will be used to derive the best sequence L*.
• Initialisation:
  • For t=1, there is no max() operation
  • Hence alpha*(i, t=1) = P( speed_t=1 given L1 = i]) * P( L1 = i)
  • In other words, alpha\*(i, t=1) == alpha(i, t=1)
• Inferrence: how to find the elements of the optimal sequence L\*?
  • Start by applying argmax() in the last column. It gives the optimal value of Lt (last state in L\*)
  • Then, for each timestep t, starting by the end, query the memory and find argmax() at t-1 that has been used to compute this alpha*.
  • This is the reason why it is important to store the transitions resulting of max() operations when builing the alpha* table.

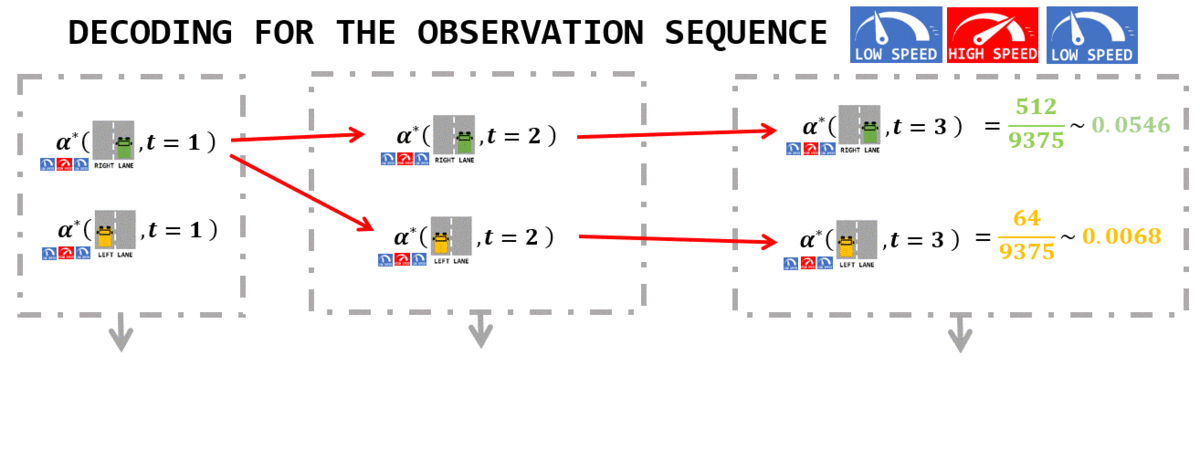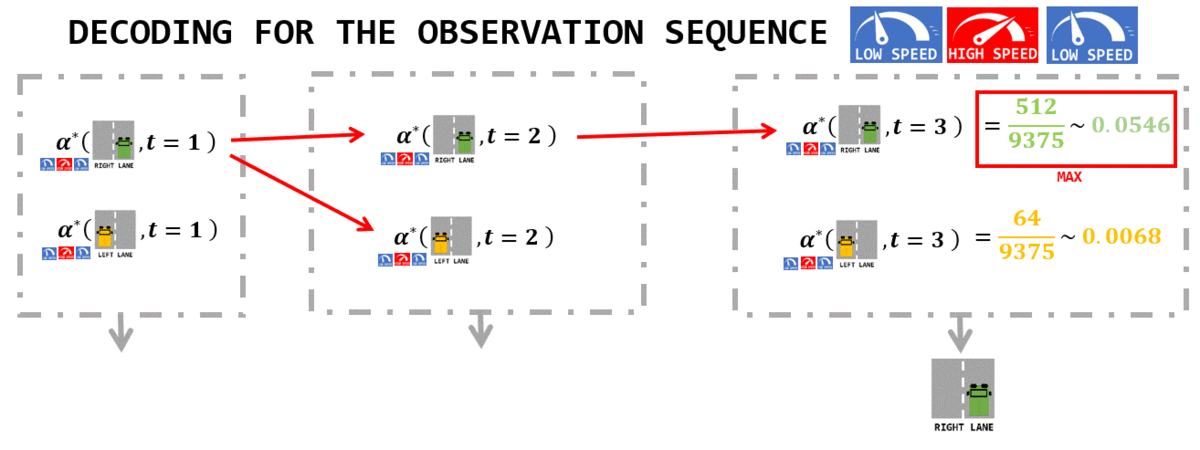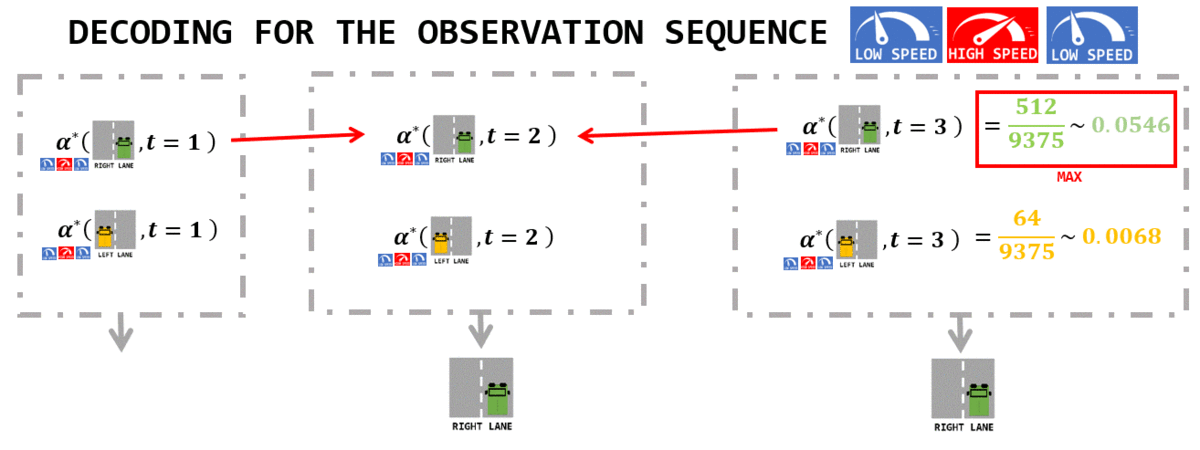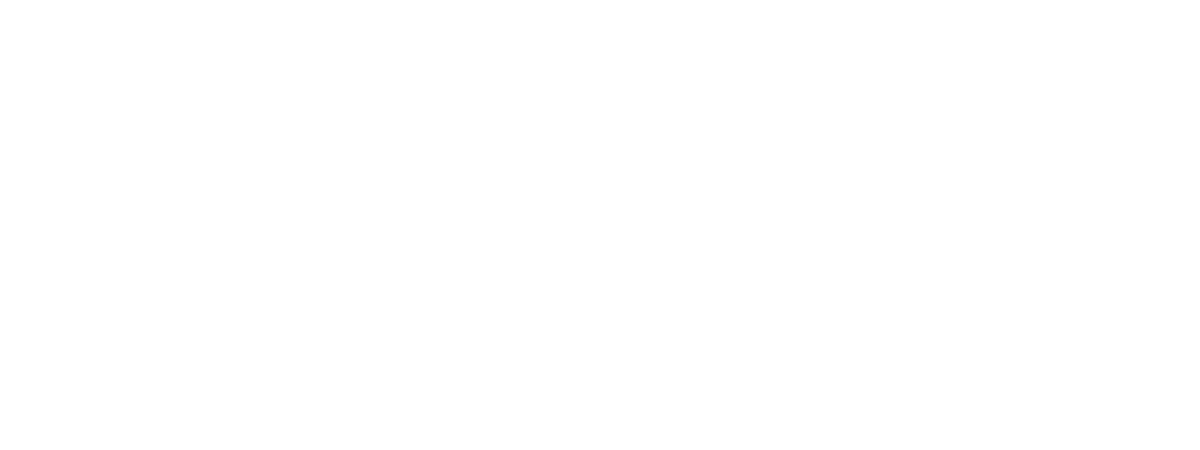
Construction of the alpha\* table using Dynamic Programming

Applying max() in the last column gives the joint probability for the most probable state sequence:

• 0.0546 = P([low speed, high speed, low speed] and [right lane, right lane, right lane])
• This result had already been found in the "naive approach" above.

Use of the alpha\* table for the marginal probability of an observation sequence

Decoding only requires only two types of information:

• The alpha* values in the last column.
• The transitions followed between columns when building the table (i.e. the argmax).

In other words, alpha\* values in the non-last columns are useless for decoding:

• No argmax() operation is performed to construct the optimal sequence from the table, except for the last column.
• It could be the case that alpha\*(left_lane, t=2) could be larger than alpha\*(right_lane, t=2).
• But that due to the transition probabilities, it is not chosen with argmax() in the next column.
  • remember that the max() operation is on the product alpha\* \* transition. Not just on alpha*.
• Nevertheless in this case alpha\*(right_lane, t=2) would still be chosen when building L* since it is located on the optimal path.

Answer:

• [right_lane, right_lane, right_lane] is the most likely lane sequence if the observation sequence is [low speed, high speed, low speed]
• this has been found using

Viterbi algorithm

• first think the HMM in the trellis representation
• then understand that we are interested in finding the best path from the start to the end (Viterby path)
  • "best" meaning the one that maximizes the cumulative probability
• to achieve that, we should first compute each trellis score (based on our trained emission and transition probability models)

Viterbi algorithm uses the Markov assumption to relax the computation of score of a best path up to position i ending in state t.

pass # notebook

Q5 - What if you are not directly given the probability models?

Trellis structure ? = any path [Sum weighting with transitions and finally emission] - Naive (consider all): 2TN^T - B-W: N^2*T Viterbi = best path [Max of (weighting with transition) and finally emission] - interested in the best sequence - max over q of P(q|obs, hmm) - if the best path ending in qt=sj, goes via qt-1=si, then it should coincide with best path ending in qt-1=si Initialisation, iteration, termination Goal: maximise P(Observation given HMM) - resolution of max: dP/dModel = 0 - iterative - Baum-Welch p(obs | hmm) = Sum over state of P(obs | state=s, hmm) * P(state=s | hmm)

Note: Generative VS Discriminative Models

The approaches used in supervised learning can be categorized into discriminative models or generative models.

Our final goal is to infer a sequence of states (let's refer to this random variable as Y) given observation (call it X). Before this inference phase (we just saw how to do it in Q4), we need:

• 1- to assume some models. We will assume some functional form for P(Y), P(X|Y)
• 2- to find their parameters (Training Phase) as we receive some data (this is Supervised Learning)

More precisely, during training:

• 1- we assume that the observed data are truly sampled from the generative model,
• 2- then we fit the parameters of the generative model to maximize the data likelihood.

In prediction (inference), given an observation, it computes the predictions for all classes and returns the class most likely to have generated the observation.

• Similar to Naive Bayes classifier, HMM tries to predict which class generated the new observed example.

Why are HMMs Generative Models?

It is possible to generate a sequence of observation from the HMM model (= Sampling)

• 1- first, sample an initial state

• 2- then, for t=2 until t=T, sample two quantities:

  • sample a new state (based on the transition model)
  • sample an observation for this state (based on the emission model)

• Another option it to first generate a state sequence (based on the transition model). Then sample for each state sample its observation (using the emission model)

• 1- During training, the goal is to estimate parameters of P(X|Y), P(Y)

  • Our model explicitly describes the prior distribution on states, not just the conditional distribution of the observation given the current state
  • It actually gives a joint distribution on states and outputs
  • Indeed before seeing any observation, we already have an idea on the Y distribution (P(Y) is our initial state probability)
  • Discriminative Models do not have any prior. They contemplate the different instances of Y and make decision based on P(Y|X) they have learnt.
  • CRFs are discriminative models which model P(y|x). As such, they do not require to explicitly model P(x) During inference, we listed all possible instance of Y and select the one that maximizes the joint probability distribution p(x,y).

• 2 - during inference we compute joint distributions before making a decision

  • Generative classifiers are interested in the joint distribution (think of Naïve Bayes, Bayesian networks, Gaussian Mixture Model, Markov random fields)
    • returns the class that as the maximum posterior probability given the features
  • While Discriminative classifiers consider either a conditional distribution (think of ‌Logistic regression) or no distribution (think of SVM, perceptron).

• 3 - Terminology

  • a generative model can be used to "generate" random instances (outcomes):

    • either of an observation and target (x, y)
    • or of an observation x given a target value y,
    • One of the advantages of generative algorithms is that you can use p(x,y) to generate new data similar to existing data.
    • it asks the question: based on my generation assumptions, which category is most likely to generate this signal?
    • takes the joint probability P(x,y), where x is the input and y is the label, and predicts the most possible known label y in Y for the unknown variable x using Bayes Rules.

  • while a discriminative model or discriminative classifier (without a model) can be used to "discriminate" the value of the target variable Y, given an observation x

    • I give you features x, you tell me the most likely class y.
    • A discriminative algorithm does not care about how the data was generated, it simply categorizes a given signal.
    • They do not need to model the distribution of the observed variables
    • They make fewer assumptions on the distributions but depend heavily on the quality of the data.
    • They direct map the given unobserved variable (target) x a class label y depended on the observed variables (training samples)
    • They try to learn which features from the training examples are most useful to discriminate between the different possible classes.

We are trying to find the parameters for multiple probabilities:

• Initial state probability: P[lane(t)]. It can be seen as the prior.

• Emission probability: P[speed(t) given lane(t)]

• Transition probability: P[lane(t+1) given lane(t)]

Generative Learning Algorithms:

• without any observation, we already know the distribution.

Here is a nice post to get an intuition of Generative an Discriminative models.

EM algorithm

Further work

Ideas to go further:

• at a crossing, make prediction of the route of other vehicles
  • route in {left, straight, right} is the hidden variable

Acknowledgement and references

I learnt and took some inspiration of

• a video series (in French) by Hugo Larochelle.
• a video by Luis Serrano.
• a series of three blog posts by David Soares Batista.

Draft

Viterbi finds the best state assignment to the sequence State1 ... StateN as a whole Posterior Decoding consists in picking the highest state posterior for each position ii in the sequence independently.

Both HMMs and linear CRFs are typically trained with Maximum Likelihood techniques such as gradient descent, Quasi-Newton methods or for HMMs with Expectation Maximization techniques (Baum-Welch algorithm). If the optimization problems are convex, these methods all yield the optimal parameter set.

https://pubweb.eng.utah.edu/~cs6961/papers/klinger-crf-intro.pdf

Label bias problem

• Only for MEMM.
• An observation can affect which destination states get the mass, but not how much total mass to pass on
• This causes a bias toward states with fewer outgoing transitions
• In the extreme case, a state with a single outgoing transition effectively ignores the observation.
• Sol: CRFs are globally re-normalized

most likely path through the HMM or MEMM would be defined as the one that is most likely to generate the observed sequence of tokens.

The basic idea is, first, to establish the probability density model of the sample, and then use the model for inference prediction The method draws from statistical mechanics and Bayes theory. HMM directly models the transition probability and phenotype probability, and calculates the probability of co-occurrence. Thus, it is a generative model.

HMM directly models the transition probability and the phenotype probability, and calculates the probability of co-occurrence. It is Bayes Rule that forms the basis of HMM. On the contrary, CRF and MEMM’s based on MaxEnt models over transition and observable features.

"Marginalize over x". Not "Marginalize x"

viterbi converts a maximization problem into a ... problem

The current state is not observable. Instead, each state produces an output with a certain probability (B). According to the above definition, βT(i) does not exist. Obviously both Forward and Backward algorithms must give the same results for total probabilities P(O) = P(o(1), o(2), ... , o(T) ).