In this question, we are asked to:
- Implement a function to generate binomial samples using functions
numpy.random.choice,numpy.sumandnumpy.array. - Calculate Variance and Expection of generated samples.
- Compare the calculated values with expected values for binomial distribution and draw their plots.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson, norm, binom
green = '#57cc99'
red = '#e56b6f'
blue = '#22577a'
yellow = '#ffca3a'
purple = '#6a4c93'
line_thickness = 3Let's define the function and call it binomial:
def binomial(n, p, test_times):
return np.sum(np.reshape(np.array(np.random.choice(2, n * test_times, p=[1 - p, p])), (test_times, n)), axis=1)Now let's calculated expected parameters and draw their plots
n = 500
m = 5000
exp_in_action = []
exp_in_theory = []
var_in_action = []
var_in_theory = []
for p in range(101):
p /= 100
q = 1 - p
sample = binomial(n, p, m)
exp_in_action.append(np.mean(sample))
exp_in_theory.append(n * p)
var_in_action.append(np.var(sample))
var_in_theory.append(n * p * q)
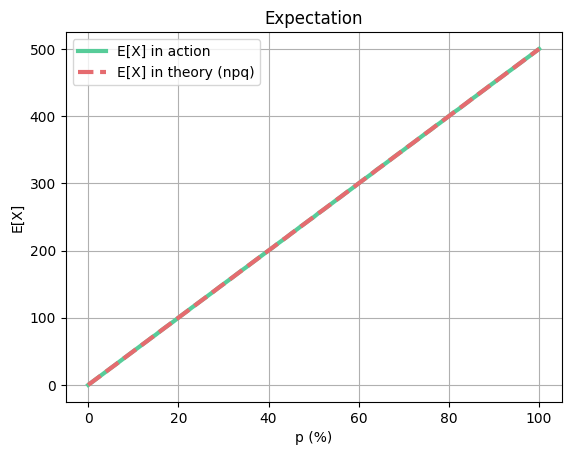
plt.title("Expectation")
x_values = range(101)
plt.xlabel("p (%)")
plt.ylabel("E[X]")
plt.plot(x_values, exp_in_action, color=green, label="E[X] in action", linewidth=line_thickness)
plt.plot(x_values, exp_in_theory, color=red, label="E[X] in theory (npq)", linestyle='--', linewidth=line_thickness)
plt.legend()
plt.grid(True)
plt.show()
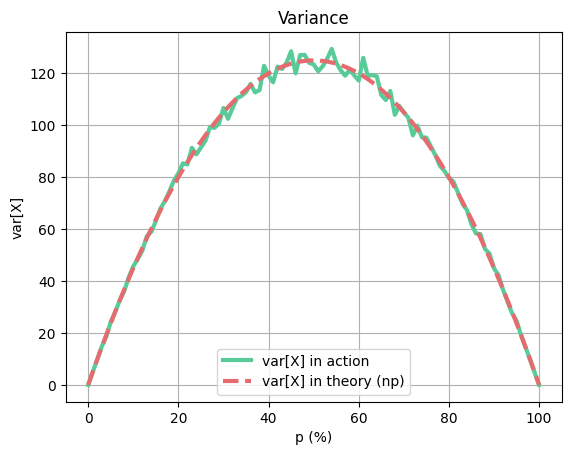
plt.title("Variance")
plt.xlabel("p (%)")
plt.ylabel("var[X]")
plt.plot(x_values, var_in_action, color=green, label="var[X] in action", linewidth=line_thickness)
plt.plot(x_values, var_in_theory, color=red, label="var[X] in theory (np)", linestyle='--', linewidth=line_thickness)
plt.legend()
plt.grid(True)
plt.show()As you can see, the expected mean and real mean are the same, but expected variance is a little bit different from
This is because as
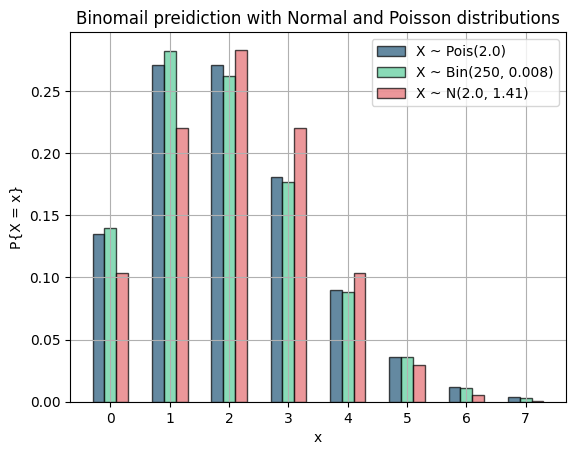
This question wants us to perdict a binomial trial with poisson and normal distributions.
n = 250
p = 0.008
q = 1 - p
mu = n * p
sigma = (n * p * q)**0.5
m = 5000
width = 0.2
x_values = np.arange(0, 8)
binomial_samples = np.random.binomial(n, p, m)
binomial_probs = [np.sum(binomial_samples == x) / m for x in x_values]
poisson_pmf = poisson.pmf(x_values, mu)
normal_pdf = norm.pdf(x_values, mu, sigma)
fig, ax = plt.subplots()
ax.bar(x_values - width, poisson_pmf, width, label='X ~ Pois({})'.format(mu), color=blue, alpha=0.7, edgecolor='black')
ax.bar(x_values, binomial_probs, width, label='X ~ Bin({}, {})'.format(n, p), color=green, alpha=0.7, edgecolor='black')
ax.bar(x_values + width, normal_pdf, width, label='X ~ N({}, {:.2f})'.format(mu, sigma), color=red, alpha=0.7, edgecolor='black')
ax.set_xticks(x_values)
ax.set_xlabel('x')
ax.set_ylabel('P{X = x}')
ax.set_title("Binomail preidiction with Normal and Poisson distributions")
ax.legend()
plt.grid(True)
plt.show()As you can see, the poisson distribution is a much better prediction for our binomial trial because
Normal distribution is better when
In this question, we are asked to find some values such that their
Note: The norm_cdf_bs function uses binary search to find
def norm_cdf_bs(mu, sigma, cdf):
l, r = 0, mu + 2000
while (r - l > 0.001):
mid = (l + r) / 2
if (norm.cdf((mid - mu) / sigma) > cdf):
r = mid
else:
l = mid
return (r + l) / 2
mu = 80
sigma = 12
min_grade = norm_cdf_bs(mu, sigma, 0.9)
x = np.arange(mu - 3 * sigma, mu + 3 * sigma, 0.01)
y = 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(- (x - mu)**2 / (2 * sigma**2))
plt.plot(x, y, color="green", label="X ~ N({}, {})".format(mu, sigma), linewidth=line_thickness)
plt.fill_between(x, y, where=(x < min_grade), color=yellow, alpha=0.3, label="F(x) = 0.9, x = {:.2f}".format(min_grade))
second_forth_start = norm_cdf_bs(mu, sigma, 0.25)
third_forth_end = norm_cdf_bs(mu, sigma, 0.75)
plt.fill_between(x, y, where=(x < third_forth_end) & (x > second_forth_start), color=red, alpha=0.3, label="0.25 < F(x) < 0.75, {:.2f} < x < {:.2f}".format(second_forth_start, third_forth_end))
plt.fill_between(x, y, where=(x < 90) & (x > 80), color=blue, alpha=0.3, label="P{{80 < X < 90}} = {:.5f}".format(norm.cdf((90 - mu) / sigma) - norm.cdf((80 - mu) / sigma)))
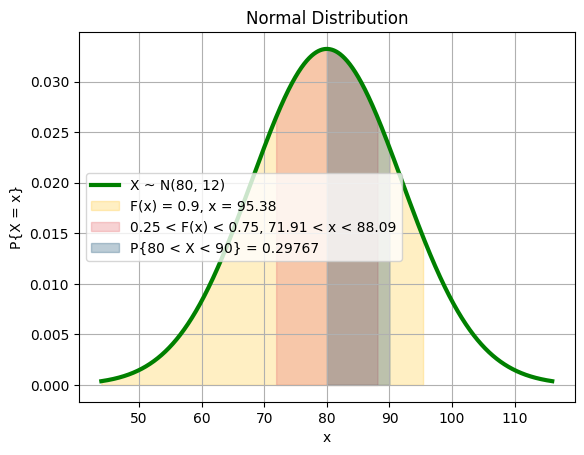
plt.title("Normal Distribution")
plt.xlabel("x")
plt.ylabel("P{X = x}")
plt.legend()
plt.grid(True)
plt.show()As we can see, the values in the center have more weights than values on the sides.
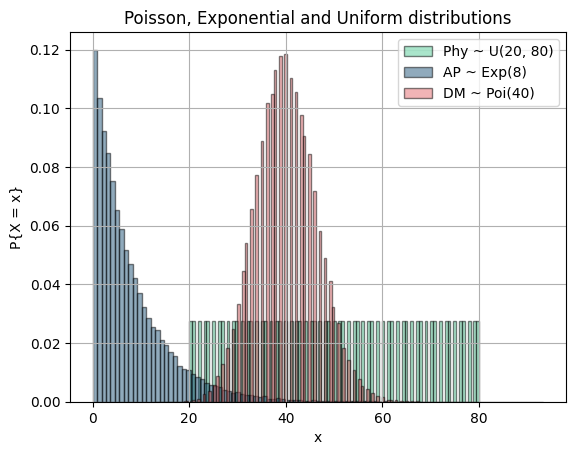
In this question, we are asked to sum 3 random variables and show that it approaches to normal distribution. Let's form our random variables samples and draw their plots:
l, r = 20, 80 + 1
repetition = 1000
size = (r - l) * repetition
physics = []
for x in range(l, r):
for t in range(repetition):
physics.append(x)
plt.hist(physics, 101, density=True, color=green, label="Phy ~ U({}, {})".format(l, r - 1), alpha=0.5, edgecolor='black')
lamb = 8
ap = np.random.exponential(lamb, size=size)
plt.hist(ap, 101, density=True, color=blue, label="AP ~ Exp({})".format(lamb), alpha=0.5, edgecolor='black')
lamb = 40
dm = np.random.poisson(lamb, size=size)
plt.hist(dm, 101, density=True, color=red, label="DM ~ Poi({})".format(lamb), alpha=0.5, edgecolor='black')
plt.title("Poisson, Exponential and Uniform distributions")
plt.xlabel("x")
plt.ylabel("P{X = x}")
plt.legend()
plt.grid(True)
plt.show()
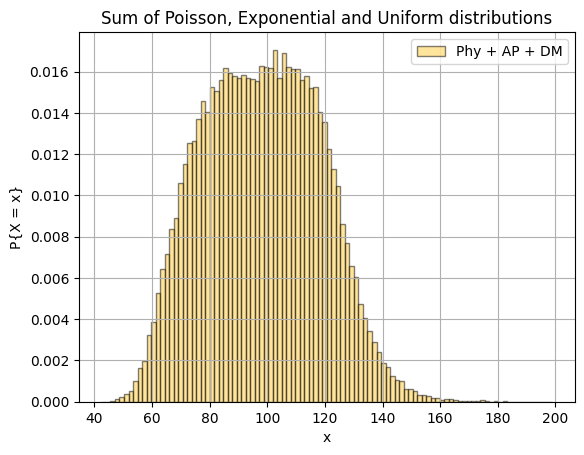
plt.hist(np.sum([physics, ap, dm], axis=0), 100, density=True, color=yellow, label="Phy + AP + DM", alpha=0.5, edgecolor='black')
plt.title("Sum of Poisson, Exponential and Uniform distributions")
plt.xlabel("x")
plt.ylabel("P{X = x}")
plt.legend()
plt.grid(True)
plt.show()Even though our 3 random variables varied in mean and variance, the product of their sum approaches to normal distribution. This is called the Central Limit Theorem.
The parameters of the normal distribution can be calculated as:
$E[X^2] = E[(Phy + AP + DM)^2] = E[Phy^2] + E[AP^2] + E[DM^2] + 2(E[PhyAP] + E[PhyDM] + E[AP*DM])$
We know that when
So, applying that rule to our equation:
So:
So, now we can say that:
Let's draw it's plot to see if it's anything close to the yellow histogram:
physics = []
for x in range(l, r):
for t in range(repetition):
physics.append(x)
ap = np.random.exponential(8, size=size)
dm = np.random.poisson(40, size=size)
mu = 90.125
sigma = 18.8
x = np.arange(40, 160, 0.01)
y = 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(- (x - mu)**2 / (2 * sigma**2))
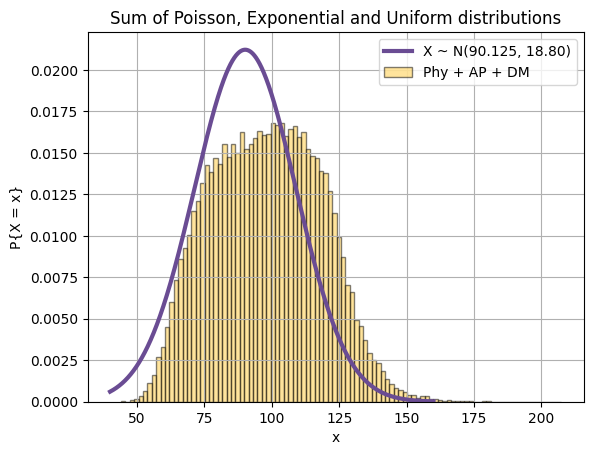
plt.plot(x, y, color=purple, label="X ~ N({}, {:.2f})".format(mu, sigma), linewidth=line_thickness)
plt.hist(np.sum([physics, ap, dm], axis=0), 100, density=True, color=yellow, label="Phy + AP + DM", alpha=0.5, edgecolor='black')
plt.title("Sum of Poisson, Exponential and Uniform distributions")
plt.xlabel("x")
plt.ylabel("P{X = x}")
plt.legend()
plt.grid(True)
plt.show()Actually that is not what I thought I would get and I'm not gonna remove it. Probably some calculation mistakes done by me. Nevermind.
This question is exactly like question 2 but with different numbers, and this time,
def draw_norm(mu, sigma, l, r):
x = np.arange(l, r, 0.01)
y = 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(- (x - mu)**2 / (2 * sigma**2))
plt.plot(x, y, color=green, label="X ~ N({}, {:.2f})".format(mu, sigma), linewidth=line_thickness)
def draw_pois(lamb, l, r):
x = np.arange(l, r, 1)
y = poisson.pmf(x, lamb)
plt.plot(x, y, color=red, label="X ~ Poi({})".format(lamb), linewidth=line_thickness)
def draw_bin(n, p, l, r):
x = np.arange(l, r)
plt.plot(x, binom.pmf(x, n, p), color=yellow, ms=8, label='X ~ Bin({}, {})'.format(n, p), linestyle='--', linewidth=line_thickness)
def draw_random_bin(n, p, size):
data = np.random.binomial(n, p, size)
num_bins = 50
counts, bins = np.histogram(data, bins=num_bins)
bins = bins[:-1] + (bins[1] - bins[0])/2
probs = counts/float(counts.sum())
plt.bar(bins, probs, 1.0/num_bins, color=blue, label="Randomized Bin({}, {})".format(n, p))
n = 7072
p = 0.45
q = 1 - p
mu = n * p
sigma = (n * p * q)**0.5
l = int(mu - 3 * sigma)
r = int(mu + 3 * sigma)
m = 30000
draw_norm(mu, sigma, l, r)
draw_pois(mu, l, r)
draw_bin(n, p, l, r)
data = np.random.binomial(n, p, m)
plt.hist(data, bins=np.arange(l, r) - 0.5, density=True, color=purple, label="Randomized Bin({}, {})".format(n, p), alpha=0.8)
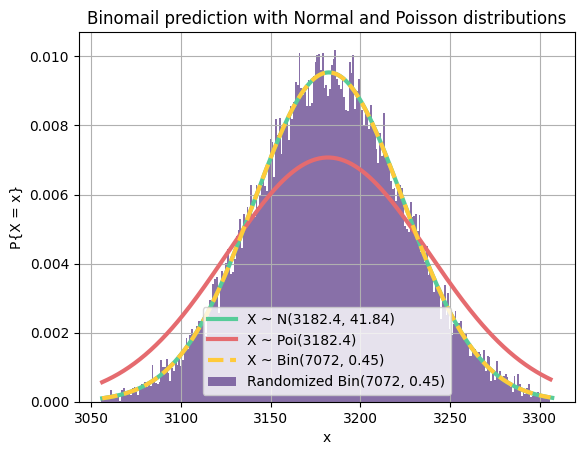
plt.title("Binomail prediction with Normal and Poisson distributions")
plt.xlabel("x")
plt.ylabel("P{X = x}")
plt.legend()
plt.grid(True)
plt.show()As you can see, normal distribution is a much better prediction for our binomial trial (purple). It also almost fits the binomial distribution plot. If we increase the number of trials, the purple area will get closer and closer to the area under the normal distribution curve.