Geometry Processing – Introduction

To get started: Clone (do not fork publicly) this repository
git clone --recursive http://github.com/alecjacobson/geometry-processing-introduction.git

Welcome to Geometry Processing! The purpose of this assignment will be to get you up and running with the two C++ libraries we will be using: Eigen for dense and sparse linear algebra routines and libigl for geometry processing routines. We will make use of the OpenGL-based viewer used by the libigl tutorial. This viewer also depends on glfw, a library for managing windows on Linux, Mac OS X and windows.

Prerequisite installation

On all platforms, we will assume you have installed cmake and a modern c++ compiler on Mac OS X¹, Linux², or Windows³.

We also assume that you have cloned this repository using the --recursive flag (if not then issue git submodule update --init --recursive).

Layout

All assignments will have a similar directory and file layout:

README.md
CMakeLists.txt
main.cpp
include/
  function1.h
  function2.h
  ...
src/
  function1.cpp
  function2.cpp
  ...
shared/
  libigl/
    include/
      igl/
        ...
  ...

The README.md file will describe the background, contents and tasks of the assignment.

The CMakeLists.txt file setups up the cmake build routine for this assignment.

The main.cpp file will include the headers in the include/ directory and link to the functions compiled in the src/ directory. This file contains the main function that is executed when the program is run from the command line.

The include/ directory contains one file for each function that you will implement as part of the assignment. Do not change these files.

The src/ directory contains empty implementations of the functions specified in the include/ directory. This is where you will implement the parts of the assignment.

The shared/ directory will contain shared resources: cmake files, dependences (e.g., libigl) and data. Feel free to poke around in here, but you shouldn't change any of these files.

Compilation

This and all following assignments will follow a typical cmake/make build routine. Starting in this directory, issue:

mkdir build
cd build
cmake ..
make

Why don't you try this right now?

Execution

Once built, you can execute the assignment from inside the build/ using

./introduction

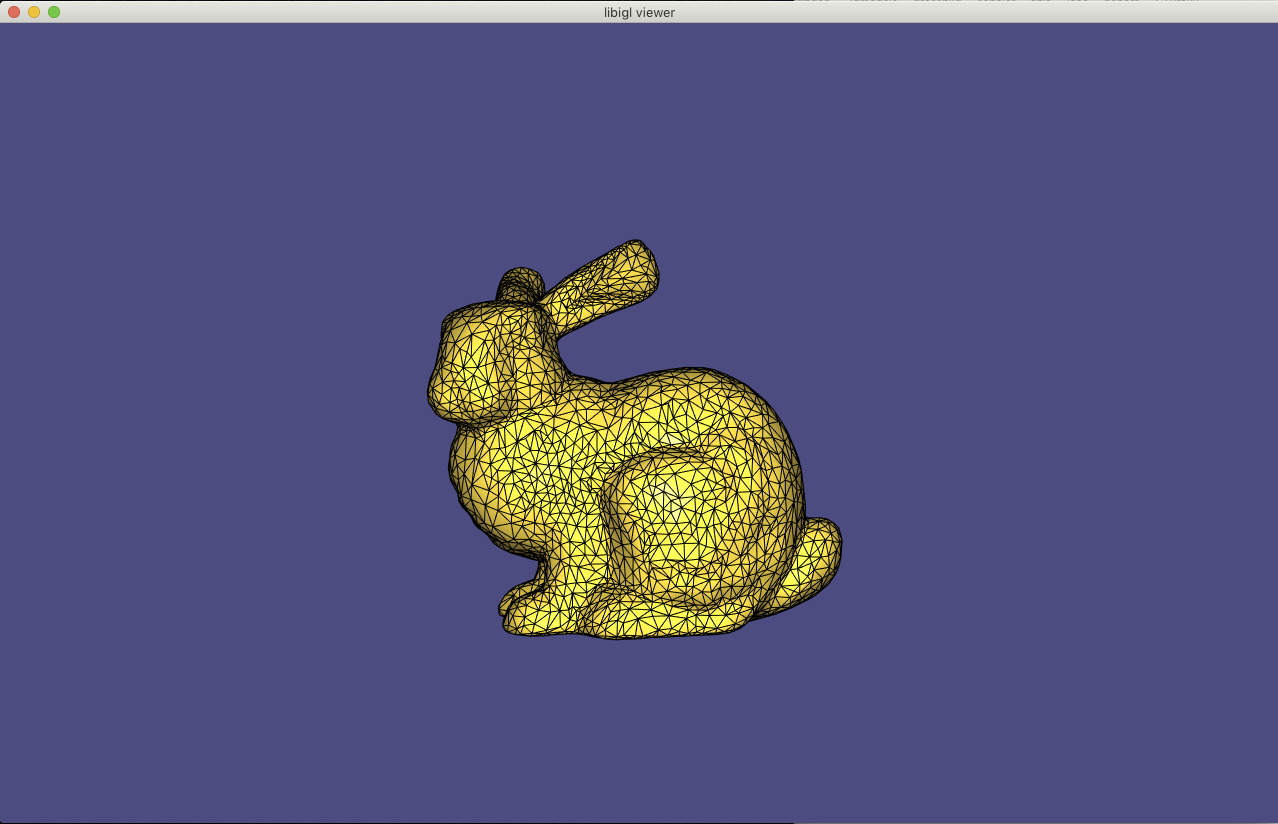
After compiling according to the instructions above, if you try executing right now, then you'll see a bunny:

You can click and drag to change the view.

Optionally, this program can input a path to a triangle mesh file (other than the bunny):

./introduction [path to input file]

Background

Every assignment, including this one, will start with a Background section. This will review the math and algorithms behind the task in the assignment. Students following the lectures should already be familiar with this material and may opt to skip this section.

Let's get familiar with the explicit mesh representation of a discrete surface immersed in $\mathbb{R}^3$. Throughout the course, we will store the set of mesh vertices $V$⁴ and the set of triangles (a.k.a. faces) $F$ as two matrices: V and F.

The matrix V is $|V|$ by 3 in size, where the ith row of this matrix contains the x-, y- and z-coordinates of the ith vertex of the mesh.

The matrix F is $|F|$ by 3 in size, where the jth row of this matrix contains the indices into the rows of V of the first, second and third corners of the jth triangle as a non-negative number (remember in C++ arrays and matrices start with index 0).

The information in V alone is purely positional and encodes the geometry of the surface.

The information in F alone is purely combinatoric and encodes the topology of the surface.

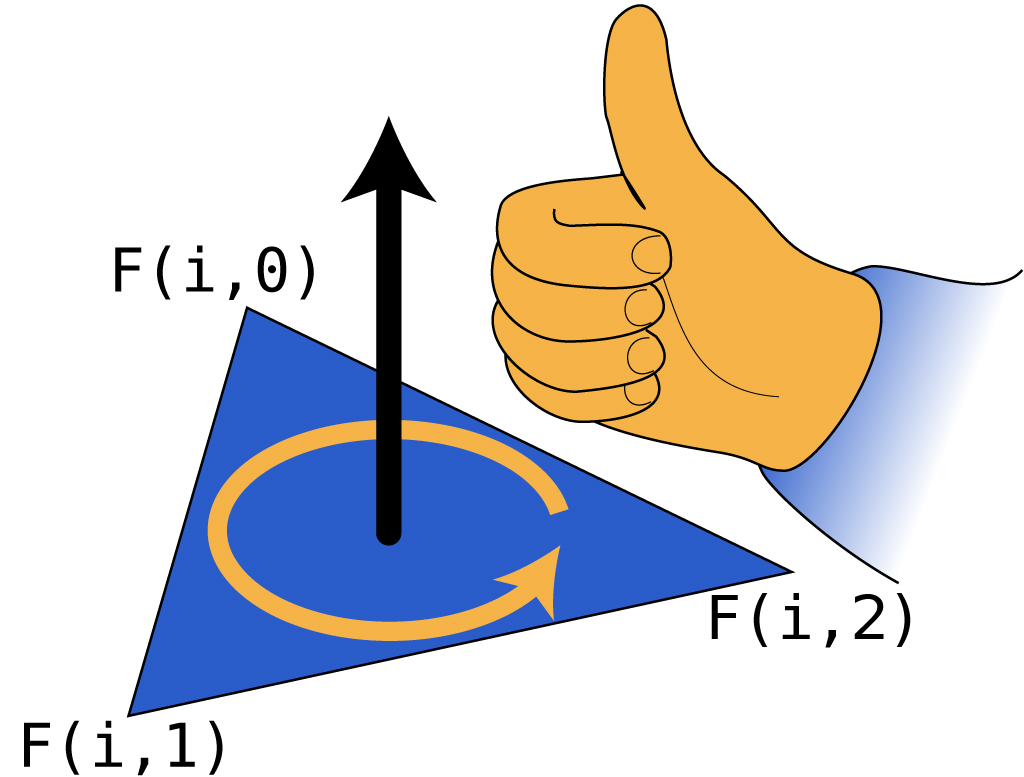
By convention, the indices in each row of F are ordered counter-clockwise around the triangle. Using the right-hand rule, we can define the normal of each triangle as the vector that points most away from the surface.

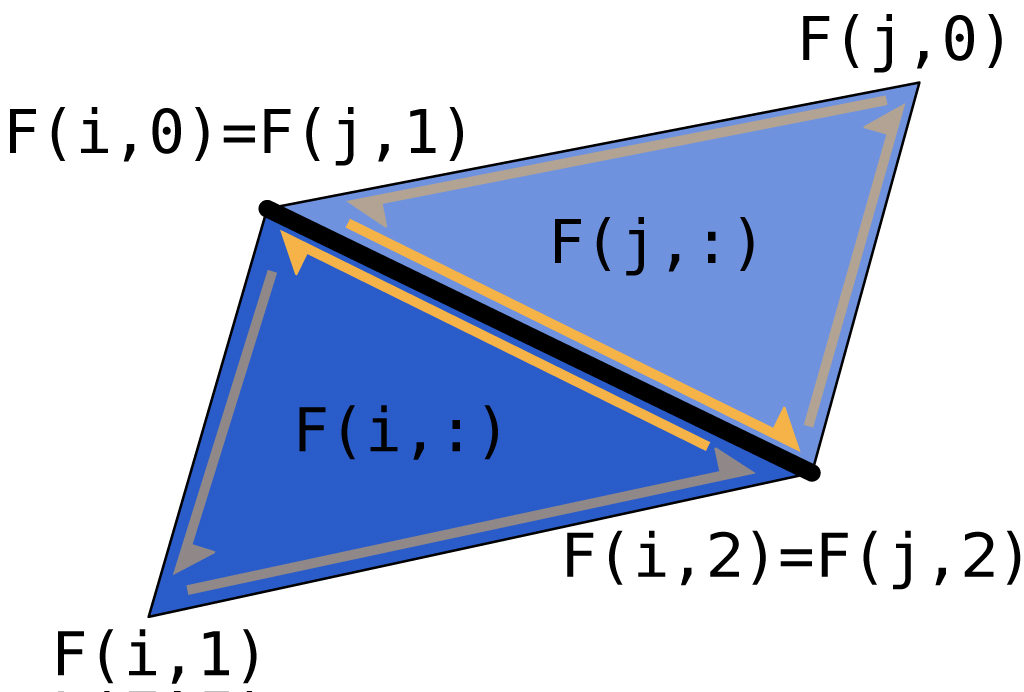
Each oriented triangle also defines three directed edges between its three vertices. Other triangles in the mesh may contain edges with the same incident vertices, possibly in the opposite direction. A manifold mesh will have at most two triangles incident on the same (undirected) edge, therefor we'll refer to each triangle's directed edge as a half-edge.

The number of vertices $|V|$ and number of faces $|F|$ and number of unique (undirected) edges $|E|$ are intimately related. Adding a new triangle to a mesh may mean increasing the number of vertices and edges, too. The algebraic relationship between the number of vertices, edges and faces reveals the topological genus of the surface via the Euler Characteristic

$$ χ = 2c - 2h - b, $$

where $c$ is the number of connected components, $h$ is number of holes (as in donut), and $b$ is the number of connected components of the boundary of the surface.

For meshes representing polyhedral surfaces, the Euler Characteristic can be computed very simply:

Chi = |V| - |E| + |F|.

Assuming no unreferenced vertices in V, each of the quantities in the right-hand side can be determined from F alone. This indicates that its a purely topological property. Changing the geometric positions (i.e., changing the vertex positions in V) will not affect the Euler Characteristic. Due to this, we say that the Euler Characteristic is a topological invariant.

Tasks

Every assignment, including this one, will contain a Tasks section. This will enumerate all of the tasks a student will need to complete for this assignment. These tasks will match the header/implementation pairs in the include//src/ directories.

Groundrules

Libigl has implemented many of the tasks you'll find in this course. As a result, for some assignments, including this one, you'll see a Groundrules section that lists which functions you can and should use from libigl and/or functions you may not use (and should avoid copying your answers from).

Blacklist libigl functions

For this assignment you may not use

igl::all_edges
igl::edge_flaps
igl::edge_topology
igl::edges
igl::euler_characteristic
igl::exterior_edges
igl::is_boundary_edge
igl::unique_edge_map
or any other libigl function that returns a list of edges.

`src/edges.cpp`

From a list of triangles F, construct a $|E|$ by 2 matrix E, where the kth row of this matrix contains the indices into the rows of V of the start and end point of the kth edge in the mesh. E should contain every undirected edge exactly once.

`src/euler_characteristic.cpp`

From the list of triangles F, return the Euler Characteristic X of the triangle mesh. You may and should use your edges function from the previous task.

Submission

Submit your src/ files on MarkUs

Questions?

Direct your questions to the Issues page of this repository.

Answers?

Help your fellow students by answering questions or positions helpful tips on the Issues page of this repository.

¹ Mac Users

You will need to install Xcode if you haven't already.

² Linux Users

Many linux distributions do not include gcc and the basic development tools in their default installation. On Ubuntu, you need to install the following packages:
sudo apt-get install git
sudo apt-get install build-essential
sudo apt-get install cmake
sudo apt-get install libx11-dev
sudo apt-get install mesa-common-dev libgl1-mesa-dev libglu1-mesa-dev
sudo apt-get install libxrandr-dev
sudo apt-get install libxi-dev
sudo apt-get install libxmu-dev
sudo apt-get install libblas-dev
³ Windows Users

libigl only supports the Microsoft Visual Studio 2015 compiler in 64bit mode. It will not work with a 32bit build and it will not work with older versions of visual studio.

⁴ LaTeX

This markdown document, and those for all other assignments, contains $\LaTeX$ math. GitHub just shows the un-evaluated LaTeX code, but other markdown browsers will show the typeset math. You can also generate README.html using multimarkdown:
cat shared/markdown/header.md README.md | multimarkdown --process-html -o README.html

LeptusHe/geometry-processing-introduction