Cloud Workflow Scheduling base on Deep Reinforcement Learning

北京化工大学本科毕业设计《基于深度强化学习的云工作流调度》

关键词：有向无环图，工作流，深度强化学习，图神经网络；蒙特卡洛树搜索

Installation

It requires the following packages:

Python 3.9.7
torch 1.10
gym 0.21.0
networkx 2.6.3

Instructions

将 Env/___.py 文件注册在gym的环境中；
运行 DAGs_generator.py 生成 train dataset， test dataset.
修改环境代码适应生成数据集的路径；
运行 PPO/DRLagent.py 训练网络；
运行 PPO/DRLtest.py 测试推理。
运行baseline_tableau.py 得出baseline算法效果
运行MonteCarloTreeSearch.py 得出MCTS算法效果

目前进度

2022.03.11

目前状态空间，动作空间下设计的Actor- Critic，PPO方法难以超越baseline Tetris的效果。
尝试经典GCN编码DAG，效果不佳。
尝试Decima中的编码结构。

2020.03.23

结合Decima中的GCN对DAG进行编码，改变编码数量，效果不佳
完成深度强化学习加速蒙特卡洛树搜索算法（魔改spear），目前在DAG_size=10大小上效果最佳。
编写了单个DAG任务资源用量检测脚本。

2020.04.19

完成蒙特卡洛树n=10-50的所有实验
完成毕业论文初稿
下一步优化GCN编码

有向无环图生成设计

工作流通常由DAG（有向无环图）来定义，其中每个计算任务$T_i$由一个顶点表示。同时，任务之间的每个数据或控制依赖性由一条加权的有向边$E_{ij}$表示。每个有向边$E_{ij}$表示$T_i$是$T_j$的父任务，$T_j$只能在其所有父任务完成后执行。一般在所有任务之前设立一个Start虚拟节点，作为所有没有父任务节点的父节点；同理，在所有任务之后设立一个Exit虚拟节点，作为所有没有子任务节点的子节点，这两个虚拟节点都没有计算资源需求。

确定表示一个DAG需要三个数据，分别是是节点连接信息，各节点的父节点数，各节点的子节点数。由这三个元素可以确定一个独立的DAG。

例如一个10个节点的DAG：

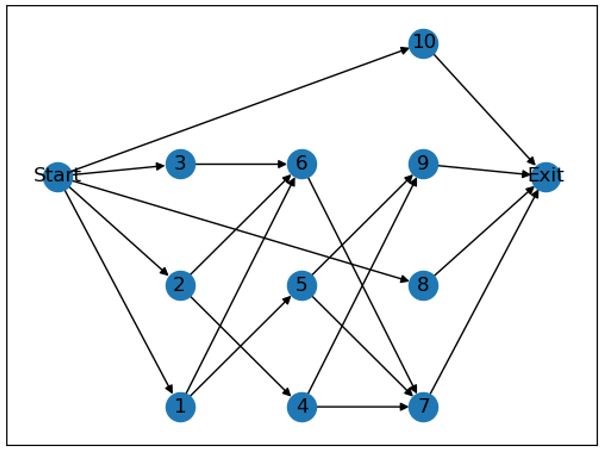
Edges: [(1, 5), (1, 6), (2, 4), (2, 6), (3, 6), (4, 7), (4, 9), (5, 9), (5, 7), (6, 7), ('Start', 1), ('Start', 2), ('Start', 3), ('Start', 8), ('Start', 10), (7, 'Exit'), (8, 'Exit'), (9, 'Exit'), (10, 'Exit')]

In_degree: [1, 1, 1, 1, 1, 3, 3, 1, 2, 1]

out_degree: [2, 2, 1, 2, 2, 1, 1, 1, 1, 1]

表示的是下面这一张图。

图 1 一个DAG示例

参数设定为：

size = [20,30,40,50,60,70,80,90] #DAG中任务的数量

max_out = [1,2,3,4,5] #DAG节点的最大出度

alpha = [0.5,1.0,1.5] #控制DAG 的形状

beta = [0.0,0.5,1.0,2.0] #控制 DAG 的规则度

具体的实现细节如下：

根据公式$length=\frac{\sqrt{size}}{alpha}$计算出生成DAG的层数，并计算平均每层的数量$\frac{size}{length}$.
在以均值为$\frac{size}{length}$，标准差为$beta$的正态分布中采样每层的任务数并向上取整，这样随机采样得到的总任务数可能有偏差，随机在某几层添加或者删除任务，使DAG总任务数等于$size$。
对于第一层到倒数第二层：每一个任务随机在[0, $max_out]$，并随机连接$n$个下一层的任务。
最后给所有没有入边的任务添加Start作为父节点，所有没有出边的任务添加Exit任务作为子节点，至此一个随机的DAG就生成好了。

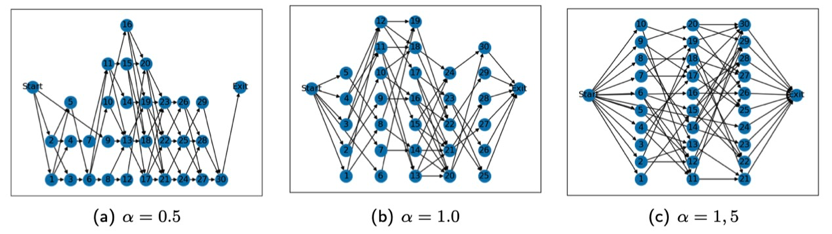
在这里$alpha$控制的是DAG的整体形状，如果$alpha$越小，DAG越长，$alpha$越大，DAG越短。

图2 不同alpha下DAG的形状（n=30）

$beta$则是控制的DAG的规则度，如果$beta$越大，DAG越参差不齐。

添加工作流信息

对DAG中每一个任务随机分配它的持续时间和资源需求（CPU，Memory）。

为了模拟一些时间占用相对较长的任务，定义一个概率prob=80%，每个任务的持续时间有80%的几率在$[t,3t]$的范围内随机取值，20%的概率在$[10t,15t]$的范围内随机取值。

每个任务有50%的概率为CPU密集型任务，剩下的50%是Memory密集型的任务。

CPU密集型的任务CPU的资源占用量在$[0.25r,0.5r]$中随机取值，Memory的资源占用量在$[0.05,0.01]$随机取值。Memory密集型的任务资源需求量相反。

举一个根据以上规则生成的工作流信息的例子，对10个任务的 DAG 随机生成的工作流信息如下表示： (r=100,t=10)

任务占用时间 Ti: [27.174, 23.215,24.209,15.085, 20.691,29.892,20.632, 26.777, 19.402,18.362]

任务资源占用 (res_cpu,res_memory): [(31.432, 1.019), (4.7330, 25.308), (1.208, 42.542), (1.517, 47.633), (39.299, 4.826), (1.654, 46.401), (2.438, 35.593), (3.887, 42.224), (1.594, 30.074), (42.445, 3.225)]

马尔可夫决策过程建模

状态空间

当前执行的时间（1维）
当前资源中剩余的 CPU 资源（1维）
当前资源中剩余的 Memory 资源（1维）
Ready_task 任务列表（长度为 10）中的任务要求时间（30维）如果不足30空位补-1
Ready_task 任务列表中的 CPU 要求资源（30维）如果不足30空位补-1
Ready_task 任务列表中的 Memory 要求资源（30维）如果不足30空位补-1
当前未完成 DAG 部分的最大路径长度（1维）
当前未完成 DAG 部分的子节点数（1维）
超出 Ready_task 任务列表长度且准备好的任务的时间要求总和（1维）
超出 Ready_task 任务列表长度且准备好的任务的 CPU 要求总和（1维）
超出 Ready_task 任务列表长度且准备好的任务的 Memory 要求总和（1维）

共98维状态。

动作空间

{-1,0,1,2,3,4,5,6,7,8,9,...,29}

•选择 $a=-1$表示执行完计算资源里的一个耗时最短的任务。此时执行时间增加该任务的消耗时间，释放占用的CPU和Memory资源。

•选择$a=0\sim29$表示把当前 Ready_task 任务列表的第a个任务提交给计算资源。此时当前执行时间不变，当前CPU/Memory资源减去该任务占用的资源。

回报函数

•选择 $a=-1$: $reward = -\frac{\text{执行时间}}{t}$

•选择$ a=0\sim9$: $reward = 0$

环境说明

实验采用OpenAI 强化学习gym平台，自定义的工作流调度环境主要包括两个函数：

state, reward, done, infor = env.step(action)

step函数用于智能体与环境进行交互，输入动作action返回的是下一步的状态state，该步的reward，是否执行完一整个个DAG任务，和动作是否有效（infor）。当接受到动作后智能体首先判断该动作是否有效：

a) 该动作对应的位置是没有任务（数据是-1），动作无效。

b) 计算资源不能能满足该位置上的任务的CPU/Memory资源需求，动作无效。

c) 如果当前计算资源中没有提交的任务,动作$a=-1$是无效的。

如果动作无效，重新采样动作；

如果动作有效，则更新状态：

a) $ a=0\sim29$ ：计算资源中CPU/Memory分别减去该任务占用的资源，更新Ready_task 任务列表中该任务对应位置上的执行时间，CPU/Memory资源全部置为-1，表示该任务已经提交给计算机。

b) $a=-1$ ：表示执行当前计算机上挂起的任务，执行的时间等于已经提交的任务列表中耗时最短的任务。例如$t=0s$时计算机上挂起了三个任务，他们执行时间分别为$23s,12s,29s$,执行$a=-1$后，第二个任务耗时最短，被执行。第一维状态就变为了12s，挂起任务执行时间列表就被更新为$11s,17s$。同时，计算资源CPU/Memory加上相应的数值，之后根据DAG结构更新Ready_task 任务列表，当前未完成 DAG 部分的最大路径长度，当前未完成 DAG 部分的子节点数等状态。

state = env.reset()

reset函数表示初始化环境，包括随机生成一个DAG并且生成工作流信息。返回的是初始38维状态。

强化学习算法与具体实现

Actor-Crtitc

采用Actor-Critic框架，伪代码如下。引入两个结构相同的网络分别作为策略网络和状态价值网络，策略网络输出的是动作的概率分布，状态价值网络输出的是当前状态的估计价值。

采用REINFORCE算法更新Actor网络，在计算target($\delta$) 时用当步的估计收益减去Critic网络的价值基线，以减小方差。

由于动作采样可能采样到无效动作（例如Ready_task 任务列表只有3个任务，动作采样到了9），当动作无效时，记录当前actor网络输出的概率分布，将采样到的动作概率置0，按照其他动作的概率重新生成分布，再从新的分布中采样动作，直到动作有效。但是在最后更新actor网络时，$\nabla_{\boldsymbol{\theta}} \log \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)$的计算还是用最开始记录的概率。

Proximal Policy Optimization

暂时未更新伪代码，代码来源https://github.com/nikhilbarhate99/PPO-PyTorch。

蒙特卡洛树搜索

蒙特卡洛树搜索是一种高效的决策规划算法，主要应用于以 (状态，行动) 定义和用模拟进行预测输出结果的领域（例如：围棋）。它是一种基于树数据结构的、在搜索空间巨大的时候仍然比较有效的搜索算法。

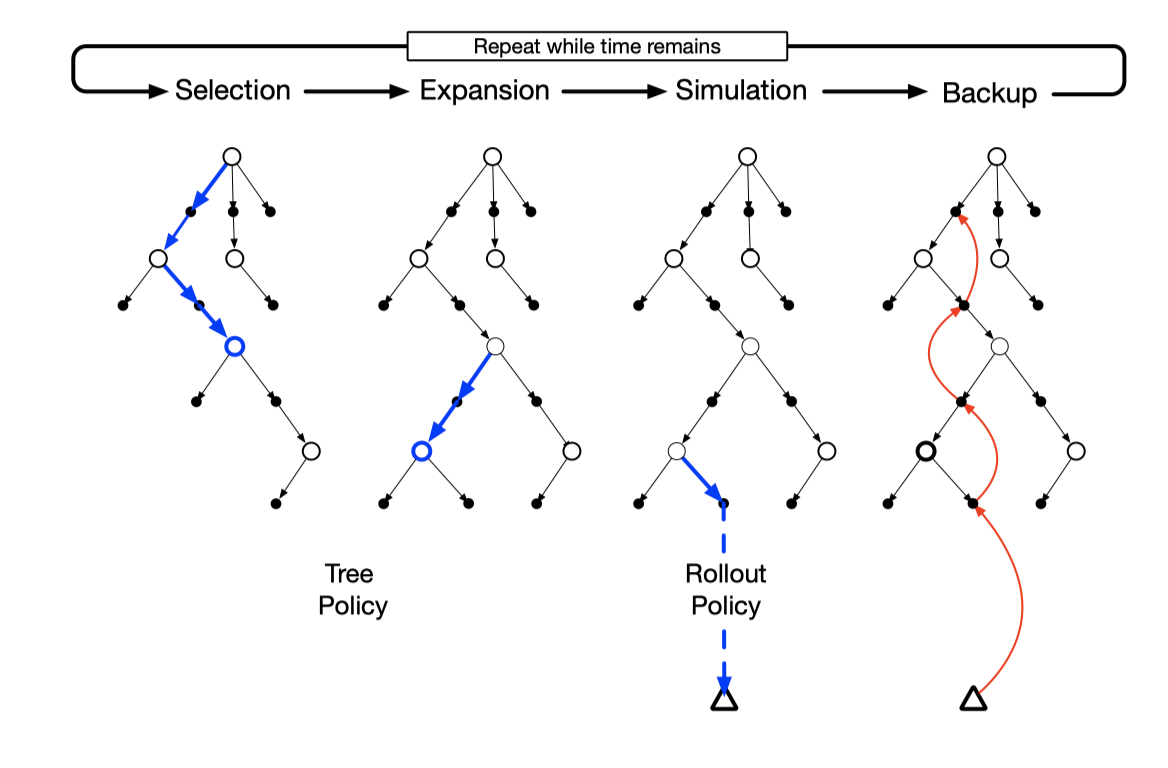
蒙特卡洛树搜索算法主要分为 4 步：选择，扩展，模拟，回溯。我们将节点分成三类：

未访问：还没有评估过当前局面
未完全展开：被评估过至少一次，但是子节点（下一步的局面）没有被全部访问过，可以进一步扩展
完全展开：子节点被全部访问过

我们找到目前认为「最有可能会走到的」一个未被评估的局面，并且选择它。

(1) 选择（seletion)：这一步会从根节点开始，根据树策略选一个“最值得搜索的叶子节点”，一般使用 Upper Conﬁdence Bound Applied to Trees(UCT) 标准选择分数最高的节点，直到来到一个“存在未扩展的子节点”的节点。

UCT: $\quad$ score $=\frac{w_{i}}{n_{i}}+c \sqrt{\frac{\ln N_{i}}{n_{i}}}$

式中 $w_i$ 是$ i$ 节点胜利次数，$n_i$ 是 $i$ 节点的模拟次数，$N_I$ 是所有模拟次数，$c$ 是探索常数，$c$ 约小越偏向于开发，$c$ 越大越偏向于试探。这个树策略函数相当于在开发和试探做权衡。

(2) 扩展（expansion）：在选择阶段结束时候，我们查找到了一个最迫切被拓展的节点 $N$，以及一个尚未拓展的动作$ A$。动作 $A $选取在这里是随机的。

(3) 模拟 (simulation)：我们从 $N_n$开始，让游戏快速地随机进行，直到得到一个游戏结局，得到的是一次蒙特卡洛实验，这个结局将作为 $N_n$的初始评分。一般使用胜利/失败来作为评分，只有 $1$ 或者$0$。模拟一般适合很快可能不是很精确的策略。比如一般的蒙特卡洛树使用随机的策略，精度不一定高，但速度快，本文使用了 DRL 辅助搜索策略，结果又快又准。

(4) 回溯 (backpropagation)：在 $N_n$的模拟结束之后，从叶节点到根节点由下到上的路径上的所有节点都会根据本次模拟的结果来更新累计评分。每一次迭代都会拓展搜索树，随着迭代次数的增加，搜索树的规模也不断增加。当到了一定的迭代次数或者时间之后结束，选择根节点下最好的子节点作为本次决策的结果。

蒙特卡洛树结合深度强化学习智能体搜索

论文：Multi-resource packing for cluster schedulers

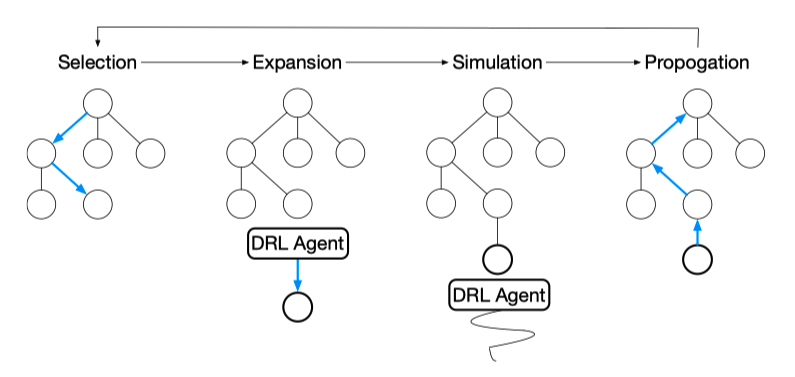
Spear 使用 DRL 加速蒙特卡洛树搜索，解决了目标是 makespan 最短的多资源需求的 DAG 问题。Spear 根据当前计算资源和任务的状态用 MCTS 搜索最佳动作，在树扩张和模拟的过程中使用 DRL 来将搜索区域缩小到更具有价值的动作空间。结果表明，Spear 在花费相同的时间内，完成时间上要短于之前最好的方法 Graphene。

Spear: 核心**：用 DRL 模型替代 MCTS 中扩展和模拟中随机选择动作的策略。有以下优点：

(1) 训练过的 DRL 模型，可以将动作搜索范围缩小到那些更快完成调度任务的动作上；

(2) 在 Simulation 中可以精准的估计每一个状态的 makespan。

改进的蒙特卡洛树搜索:

(1) 选择：将UCT公式中的前一项改为最大的 reward，也就是：

score $=\max {I}+c \sqrt{\frac{\ln N{i}}{n_{i}}}$

(2) 扩展: 当前状态下有许多动作都是没必要探索的，传统的 MCTS 使用随机策略选择动作，很显然是不高效的。不过，训练好的 DRL 模型可以高效的选择未被探索过的动作，根据策略网络输出动作的概率，makespan 越小的动作具有越高的概率。

(3) 模拟：同样使用训练好的 DRL 模型来选择动作，这提供了更有意义的 makespan 估计。

(4)回溯：更新从叶节点到根节点路径上所有节点的值：max{current_value, new_value } ，并且记录该节点上 value 的平均值。
The budget（控制树搜索次数）：$\max \left(\frac{b_{i n i t i a l}}{d_{i}}, b_{\min }\right)$

$d_i$ 是目前树的深度，$b_{initial}$ 是初始迭代预算次数，$b_min$ 是最小迭代预算次数。

实验

对比方法

Shortest Job First（SJF）：首先选择耗时最短的任务执行。SJF首先按可执行任务的时间从小到大排序，将任务放入计算资源中直到放不下后，再执行动作$a=-1$
Random：在{-1,0,1,2,3,4,5,6,7,8,9}中随机执行动作，若遇到无效动作重新随机。
Tetris: Multi-Resource Packing for Cluster Schedulers 中为最小makespan设计的策略。

Tetris

Tetris, a cluster scheduler that packs tasks to machines based on their requirements along multiple resources.

objectives：

$\bullet$Packing Efficiency for Makespan

$\bullet$Average Completion Time

$\bullet$Fairness

现在Ready task列表中有2个任务，CPU和memory需求资源分别为: $[t_1:(31.432, 1.019), t_{2}:(4.733, 25.308)，t_{3}:(15.000, 1.019)]$

假设当前资源中CPU和memory剩余的资源为(30,60)。

计算任务的Alignment Score：

$$AS_2 = (4.733,25.308)\cdot (30,60) = 4.733\times 30+25.308\times 60 = 1660.47$$

$$AS_3 = (15.000,1.019)\cdot (30,60) = 15.000\times 30+1.019\times 60 = 511.14$$

因为$AS_{2}>AS_{3}$，因此先选择$t_{2}$执行。

在每次选择动作的时候，计算ready task中的每一个任务的Alignment Score，选择最大AC的任务放在计算资源上，然后重复计算，放置，直到计算资源上不能再容纳更多的任务，这时候动作$a=-1$。

在只考虑makespan时不一定能减少任务的平均完成时间。例如：

Machines have 2 cores and 4GB of memory.

$t_{1} $ 有6个任务，每个任务需要 [2 cores, 3 GB], $t_{2}$有两个任务，每个任务需要 [1 cores, 2 GB]

如果按照alignment score的方法的计算，先执行$t_1$，再执行$t_{2}$,这样的话很明显平均任务完成时间要比先先执行$t_1$再执行$t_{2}$的长。、

一种常见的减少任务平均完成时间的算法就是Shortest Job First(SJF)。

为了同时优化Makespan和average completion time两个目标，定义分数：$(a+\varepsilon \cdot p)$

式中，$\varepsilon=(\bar{a} / \bar{p})$，$a$ 表示 alignment score，$p$表示任务持续时间。

以上三种方法均在同样的gym环境中交互，这意味着SJF方法知道Ready_task 任务列表30个长度的信息。

最终实验结果

N=10