HamilToniQ: Comprehensive Optimization and Benchmarking for Mixer Hamiltonian in QAOA with Error Mitigation
This is the repository for IBM Quantum Hackathon 2023 at the World of Quantum with the topic of encoding (Mixer Hamiltonian). More detailed description can be found here.
This project includes the following parts:
- Problem Formulation
- Mixer Hamiltonian Formulation
- Post-processing of mixer Hamiltonian
- Error mitigation
- QAOA Circuit Depth Reduction
- QASM, Noisy Simulator and Real Hardware Benchmark
Quantum computing is an emerging field with the potential to revolutionize various sectors. The Quantum Approximate Optimization Algorithm (QAOA) is a promising quantum algorithm for near-term devices, but its performance is often limited by the depth of the quantum circuit (Hamiltonian Formation). To address this, we are developing an open-source benchmarking kit for QAOA based on Qiskit, a popular quantum computing framework. This project, the first of its kind on GitHub, will focus on depth reduction techniques for QAOA circuits to improve their performance on real quantum devices. Additionally, we will leverage the Qiskit Runtime function and incorporate error mitigation techniques, enabling comprehensive benchmarking on both Qiskit's simulators and real quantum hardware. Our project aims to contribute to the practical development of quantum computing by providing a valuable resource for the quantum computing community.
The Quantum Approximate Optimization Algorithm (QAOA)is a hybrid quantum-classical algorithm that has been proposed as a practical method to solve combinatorial optimization problems on near-term, noisy intermediate-scale quantum (NISQ) devices. QAOA operates by approximating the ground state of a problem Hamiltonian (H_P), which encodes the optimization problem to be solved. The algorithm first evolves the initial state through repeated, alternating application of mixer Hamiltonians and phase separations. The expectation value with respect to this final state is evaluated. If the expectation value meets the required tolerance, the algortihm stops. If not, the expectation value is passed to a classical optimizer, which alters the parameters of the mixer and phase separation operators. The process is then repeated with these new parameters until the expectation value is minimized.

We study Quantum Approximate Optimization Algorithm (QAOA) on three distinct
problem types: Hardware Grid problem, the Three Regular problem, and the Sherrington-Kirkpatrick (SK) model problem.

- SK model is a well-known model in statistical mechanics, representing a system of spins with random interactions. In the context of QAOA, the SK model problem is a fully connected graph, where each node (or spin) can interact with every other.
- Three Regular problem has each node in the graph connected to exactly three others, forming a ’3-regular’ graph. It represents a balance between the highly constrained hardware grid problem and the fully connected SK model problem.
- Hardware Grid problem represents physical layout of qubits in quantum hardware. The qubits are arranged in a two-dimensional grid, and interactions are allowed between neighboring qubits. This problem type is particularly relevant for near-term quantum devices, as it mirrors the connectivity constraints of actual quantum hardware.
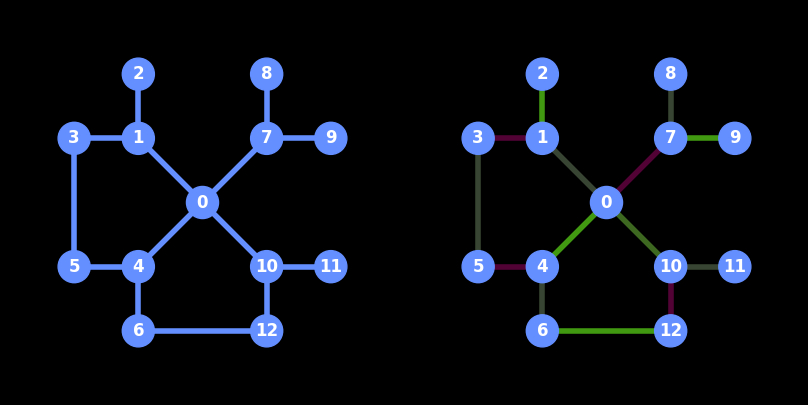
To avoid increased depth and a huge ammount of SWAP gates when implementing XY mixers we find the best strategy for each coupling map. We divide coupling map group into multiply sub groups, such that the pairs in each sub group indicate the qubits where XY mixers are applied on at the same time. And our goal is to find the minimum nuumber of subgroups. This condition can be transformed as two constraints on sub groups: (1) sub groups are complete (2) there is no deplication of qubits in every sub group.
This problem can be viewed as a variant of the graph colouring problem, where the goal is to assign colours to the vertices of a graph such that no two adjacent vertices share the same colour. In the context of the coupling optimization problem, the "colours" are the steps in which the XY mixers are applied. Our algorithm, find_sub_group will automatic help us to devide the group and find the optimal sequence of applying XY mixers. The figure below shows an example of the results.
We compare X and XY mixers with and without error mitigation by setting the resilience_level to 0 (no error mitigation) or 1 ( error mitigation). Particular error mitigation we used was twirled readout error extinction (T-REx). This ansatz makes no assumption about the type of noise in the system, and is therefore generally effective [3].
The picture below compares four different mixers applied to three different problems executed on noise-free simulators 'qasm' and 'aer' and on a noisy simulator. We also queued the job for executing it on real hardware but the queue was too long to get the results in time. The colourmap is defined in a way that a dark spot corresponds to low energy. Therefore the solution set of possible ground states is restricted by the colourmaps. The X-mixer restricts the solution set only minor but the ring, parity and full mixer improve the result significantly. In the rightmost picture, one can identify the noise by comparing the X-mixer results with the noise-free simulation.
In the results above the quantum circuit was measured directly which introduces sampling errors. In order to prevent these errors one can directly compute the state vector of the quantum circuit. This leads to a significant improvement in the plot because the periodic structure of the different mixers can be seen. Furthermore, it is now possible to identify the possible ground states by the dark spots on the colourmap. So for example in the standard problem, we could reduce the possible ground states from eight to two with two side peaks. In the case of the three-regular problem, the possible ground states could be reduced by half. As the SK model is completely symmetric and the amount of excitations is preserved in the XY-mixer the colormap needs to be completely flat.
In conclusion, our project, HamilToniQ, provides a comprehensive approach to optimizing and benchmarking the mixer Hamiltonian in QAOA with error mitigation. We have explored three distinct problem types: Hardware Grid, Three Regular, and Sherrington-Kirkpatrick (SK) model problems. Our approach includes a novel strategy for reducing the depth of the quantum circuit, which is a critical factor in the performance of QAOA on real quantum devices. We have also incorporated error mitigation techniques, specifically twirled readout error extinction (T-REx), to further enhance the performance. Our benchmarking results, obtained from both simulators and real quantum hardware, demonstrate the effectiveness of our approach. By providing this open-source benchmarking kit, we aim to contribute to the practical development of quantum computing and provide a valuable resource for the quantum computing community.
Required packages to run the code are listed in requirements.txt and can be installed by running:
pip install -r requirements.txt
(1) Benchmarking the performance of portfolio optimization with QAOA https://arxiv.org/abs/2207.10555
(2) A Quantum Approximate Optimization Algorithm https://arxiv.org/abs/1411.4028
(3) Model-free readout-error mitigation for quantum expectation values https://arxiv.org/abs/2012.09738