CGA2M+ (Constraint GA2M plus)

We propose Constraint GA2M+ (CGA2M+), which is a modification of GA2M designed to improve both its interpretability and accuracy. For more information, please refer to our paper. Mainly, CGA2M+ differs from GA2M in two ways:

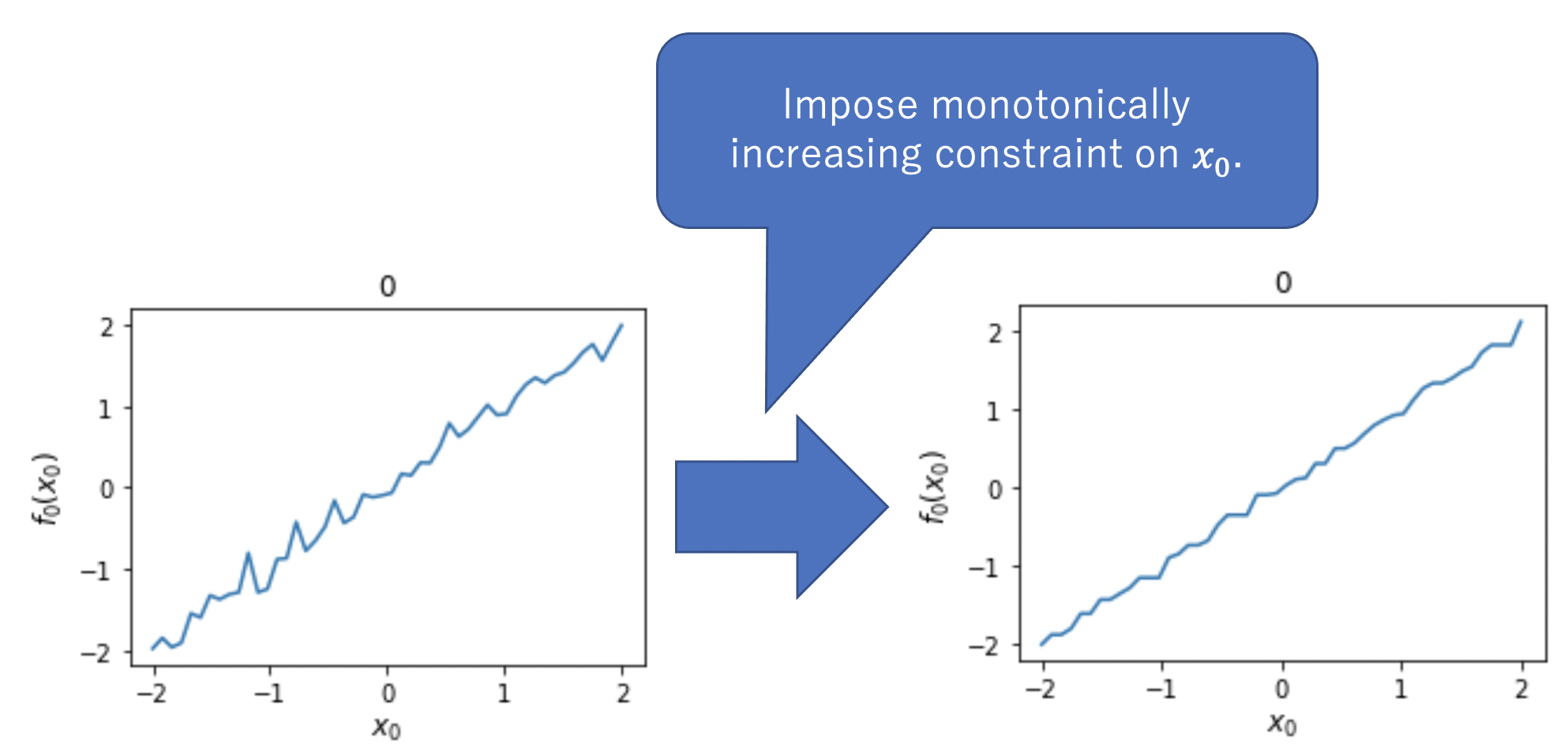
It introduces monotonic constraints.
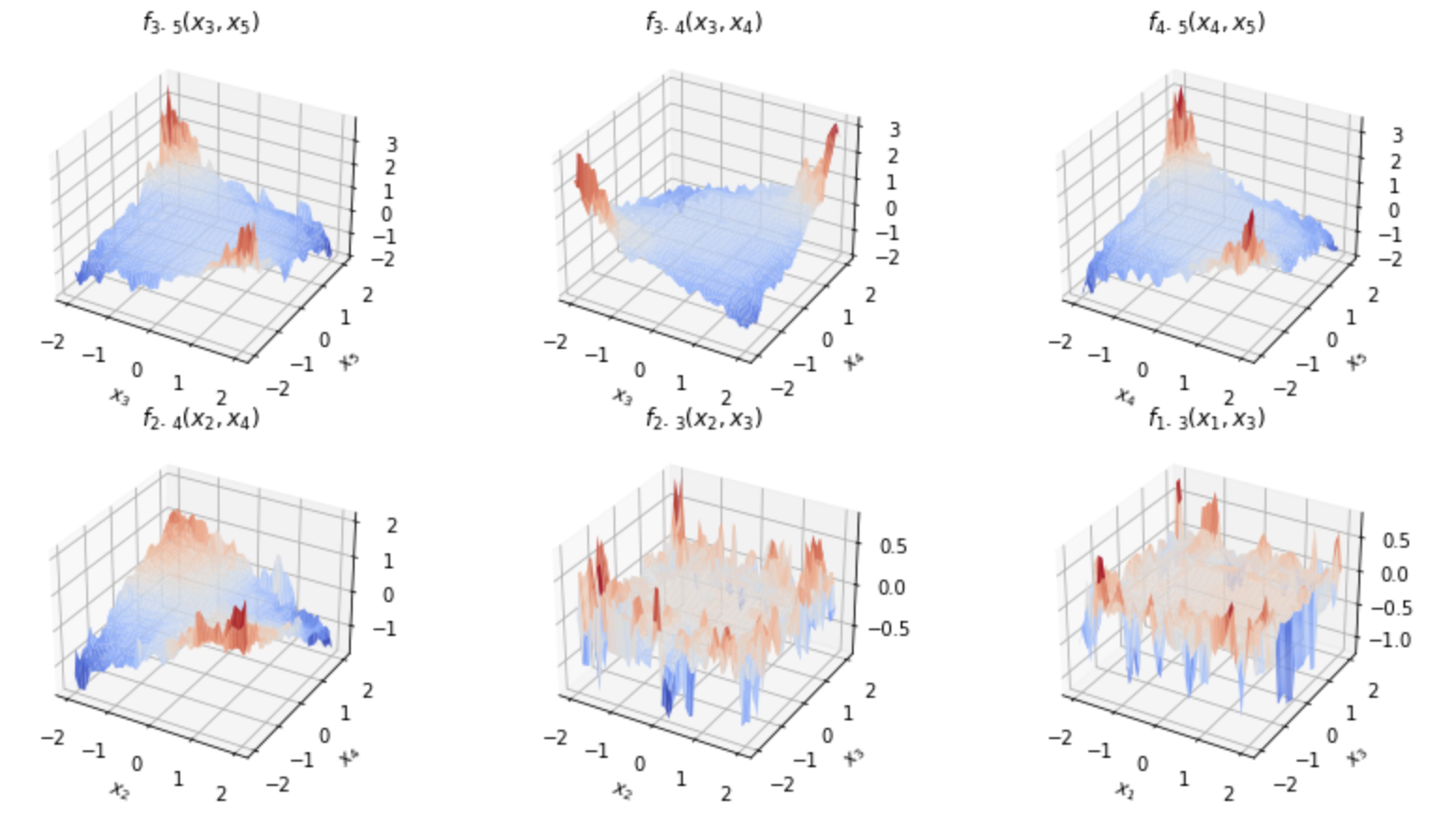
It introduces higher-order interactions while maintaining the interpretability of the model.

Description of CGA2M+

Mainly, CGA2M+ differs from GA2M in two respects. We are utilizing LightGBM as a shape function.

Mainly, CGA2M+ differs from GA2M in two respects. We are using LightGBM as a shape function.

1. Introducing Monotonic Constraints

By incorporating monotonicity, we can enhance the interpretability of our model. For instance, we can ensure that scenarios like "in the real estate market, as the number of rooms increases, the price decreases" do not occur. The determination of which features should exhibit monotonicity requires human knowledge. The algorithm for imposing monotonicity constraints is implemented in LightGBM. It provides a means to restrict the branches of a tree. For further details, please refer to the LightGBM implementation.

2. Introducing Higher-Order Interactions while Maintaining Model Interpretability

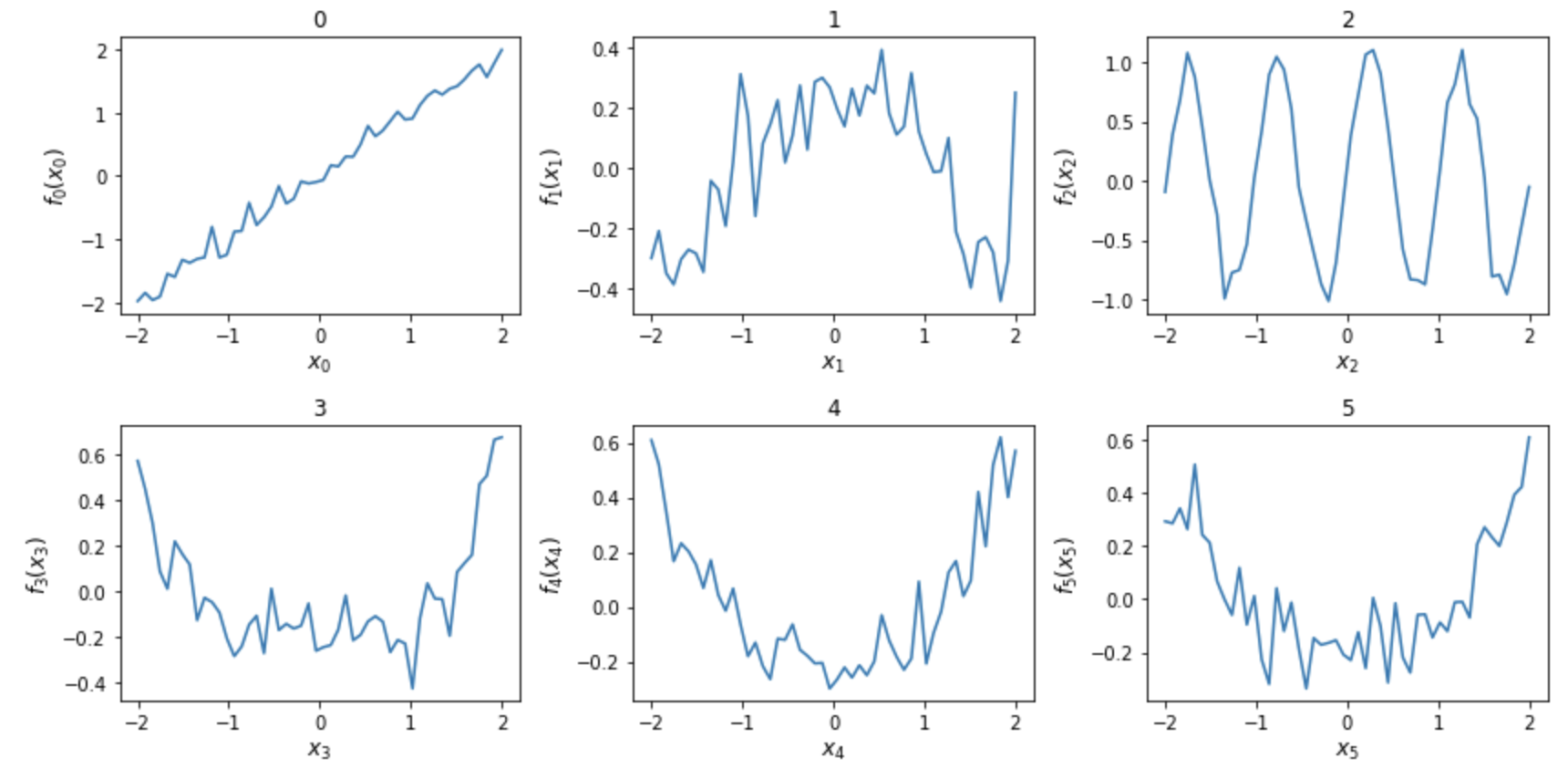
GA2M is limited in its ability to capture higher-order interactions. To address this limitation, we introduce higher-order terms that, on their own, lack interpretability. However, we have devised a learning method that ensures these higher-order terms do not compromise the overall interpretability of the model.

Specifically, we train the higher-order terms as models responsible for predicting the residuals of the univariate terms and pairwise interaction terms. By doing so, we ensure that the majority of predictions can still be explained by the interpretable first and second order terms. The residuals, representing the unexplained portions, are then predicted by the higher-order term.

Algorithm

For more information, please read our paper. (coming soon!!)

Installation

You can get CGA2M+ from PyPI. Our project in PyPI is here.

pip install cga2m-plus

Usage

For more detail, please read examples/How_to_use_CGA2M+.ipynb. If it doesn't render at all in github, please click here.

Training

cga2m = Constraint_GA2M(X_train,
                        y_train,
                        X_eval,
                        y_eval,
                        lgbm_params,
                        monotone_constraints = [0] * 6,
                        all_interaction_features = list(itertools.combinations(range(X_test.shape[1]), 2)))

cga2m.train(max_outer_iteration=20,backfitting_iteration=20,threshold=0.05)
cga2m.prune_and_retrain(threshold=0.05,backfitting_iteration=30)
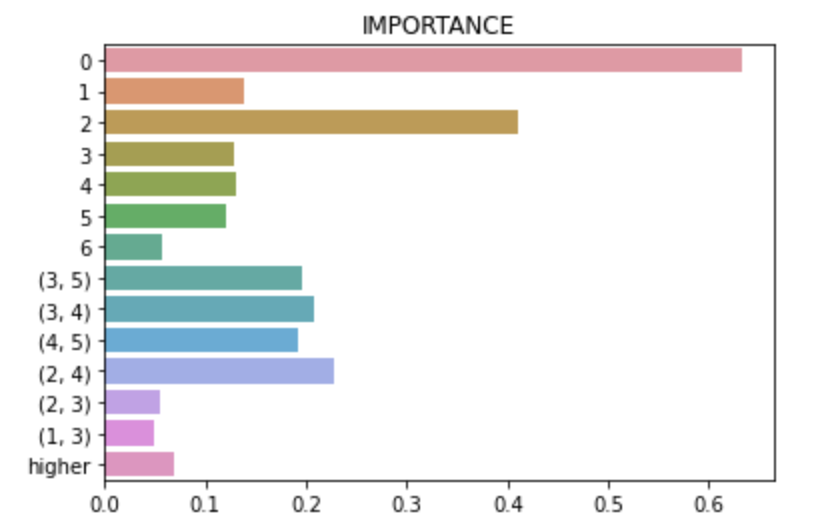
cga2m.higher_order_train()

Predict

cga2m.predict(X_test,higher_mode=True)

Visualize the effect of features on the target variables.

plot_main(cga2m_no1,X_train)

Visualize (3d) the effect of pairs of features on the target variables

plot_interaction(cga2m_no1,X_train,mode = "3d")

Feature importance

show_importance(cga2m_no1,after_prune=True,higher_mode=True)

License

MIT License

Citation

You may use our package(CGA2M+) under MIT License. If you use this program in your research then please cite:

CGA2M+ Package

@misc{kuramata2021cga2mplus,
  author = {Michiya, Kuramata and Akihisa, Watanabe and Kaito, Majima 
            and Haruka, Kiyohara and Kensyo, Kondo and Kazuhide, Nakata},
  title = {Constraint GA2M plus},
  year = {2021},
  publisher = {GitHub},
  journal = {GitHub repository},
  howpublished = {\url{https://github.com/MK-tech20/CGA2M_plus}}
}

CGA2M+ Paper [ link ]

@INPROCEEDINGS{9698779,
  author={Watanabe, Akihisa and Kuramata, Michiya and Majima, Kaito and Kiyohara, Haruka and Kensho, Kondo and Nakata, Kazuhide},
  booktitle={2021 International Conference on Electrical, Computer and Energy Technologies (ICECET)}, 
  title={Constrained Generalized Additive 2 Model With Consideration of High-Order Interactions}, 
  year={2021},
  volume={},
  number={},
  pages={1-6},
  doi={10.1109/ICECET52533.2021.9698779}}

Reference

[1] Friedman, J. H. 2001, Greedy function approximation: a gradient boosting machine, Annals of statistics, 1189-1232, doi: 10.1214/aos/1013203451. Available online: May 02, 2021

[2] Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., ... Liu, T. Y. 2017. Lightgbm: A highly efficient gradient boosting decision tree, Advances in neural information processing systems(NIPS’17), Long Beach California , 4-9 December, pp. 3146-3154.

[3] Nelder, J. A., Wedderburn, R. W. 1972. Generalized linear models, Journal of the Royal Statistical Society: Series A (General), 135(3), 370-384, doi: 10.2307/2344614, Available online: May 02, 2021

[4] Hastie, T. J., Tibshirani, R. J. 1990. Generalized additive models (Vol. 43), CRC press, doi: 10.1214/ss/1177013604. Available online: May 02, 2021

[5] Lou, Y., Caruana, R., Gehrke, J., Hooker, G. 2013, August. Accurate intelligible models with pairwise interactions, Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining(KDD’13), Chicago Illinois, United States of America, 11-14 August, pp. 623-631.

[6] “GitHub - microsoft/LightGBM” [Online]. Available: https://github.com/microsoft/LightGBM (Accessed: May 02, 2021)

[7] “scikit-learn: machine learning in Python — scikit-learn 0.24.2 documentation” [Online]. Available: https://scikit-learn.org/stable/ (Accessed May 02, 2021)