Scaling Diffusion Transformers Efficiently via μP

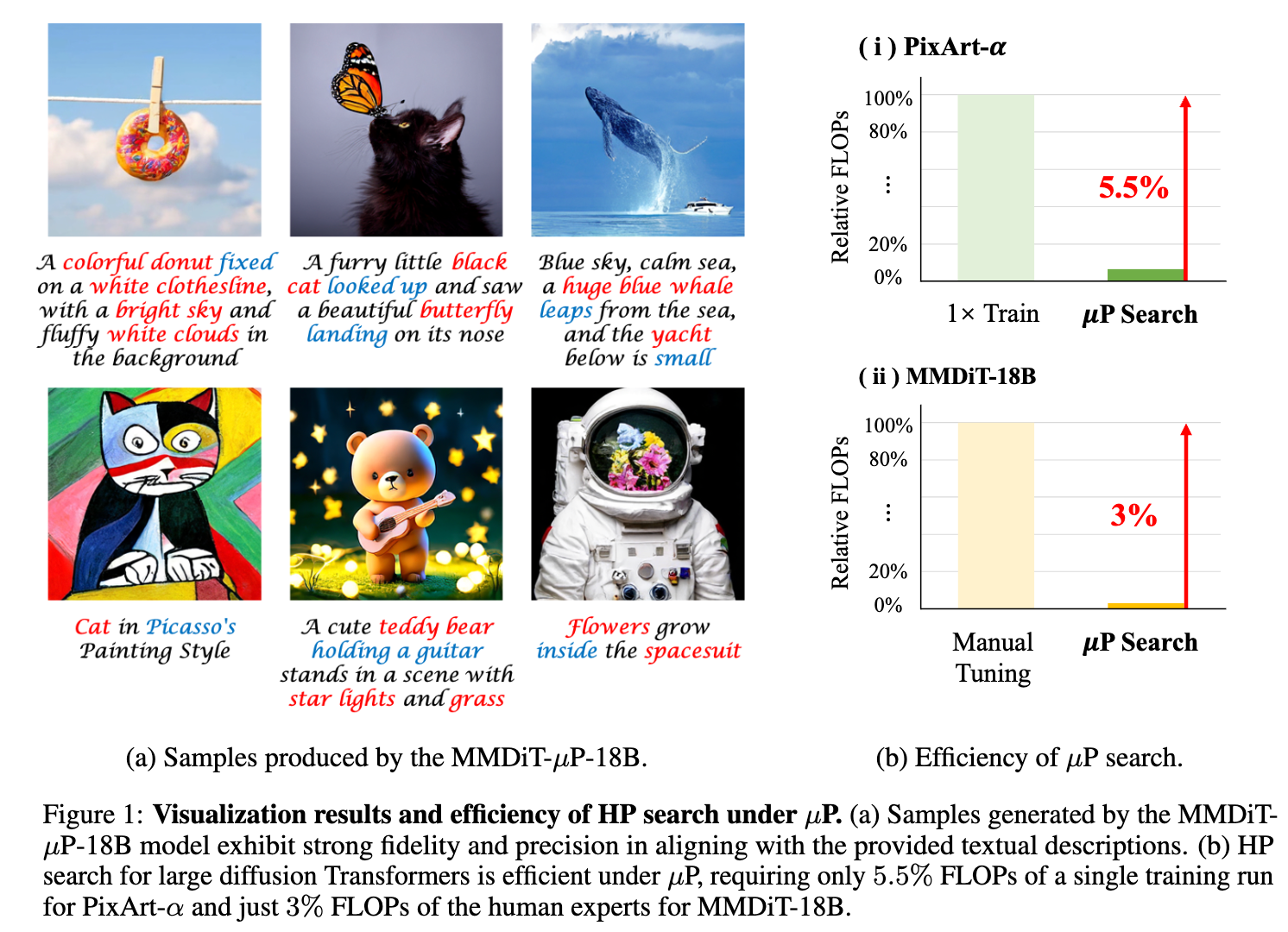
This is the official implementation for our paper "Scaling Diffusion Transformers Efficiently via μP". We verify that μP enables stable hyperparameter (HP) transfer from small to large diffusion Transformers, and dramatically reduces HP tuning costs at scale. As a result, diffusion Transformers under μP outperform their respective baselines while requiring small tuning cost (e.g., 3% FLOPs of human experts for MMDiT-18B).

News

2025/06/27: We release the checkpoints of DiT-XL-2-μP and PixArt-α-μP at https://huggingface.co/GSAI-ML/DiT-muP.
2025/05/21: We release the code of DiT and PixArt-α.

What is μP?

Maximal Update Parametrization (μP) was recently proposed as a promising solution to the HP selection problem for large models (e.g., vanilla Transformer). It stabilizes optimal HPs across different model widths, enabling direct transfer of HPs searched from small models to large models (a.k.a., μTransfer algorithm) and significantly reducing tuning costs at scale. Due to its strong transferability, μP has been applied to the pretraining of large language models (LLMs).

μP analytically adjusts the HPs of each weight based on the model's width and weight type (input, hidden, or output). These adjustments typically involve the weight multiplier, initialization variance, and learning rate. The implementation of μP is explained in detail in our paper and in the original Maximal Update Parametrization (μP) repository.

What are our contributions?

We rigorously prove that μP of mainstream diffusion Transformers aligns with the existing framework, enabling the direct application of existing μP methodologies .
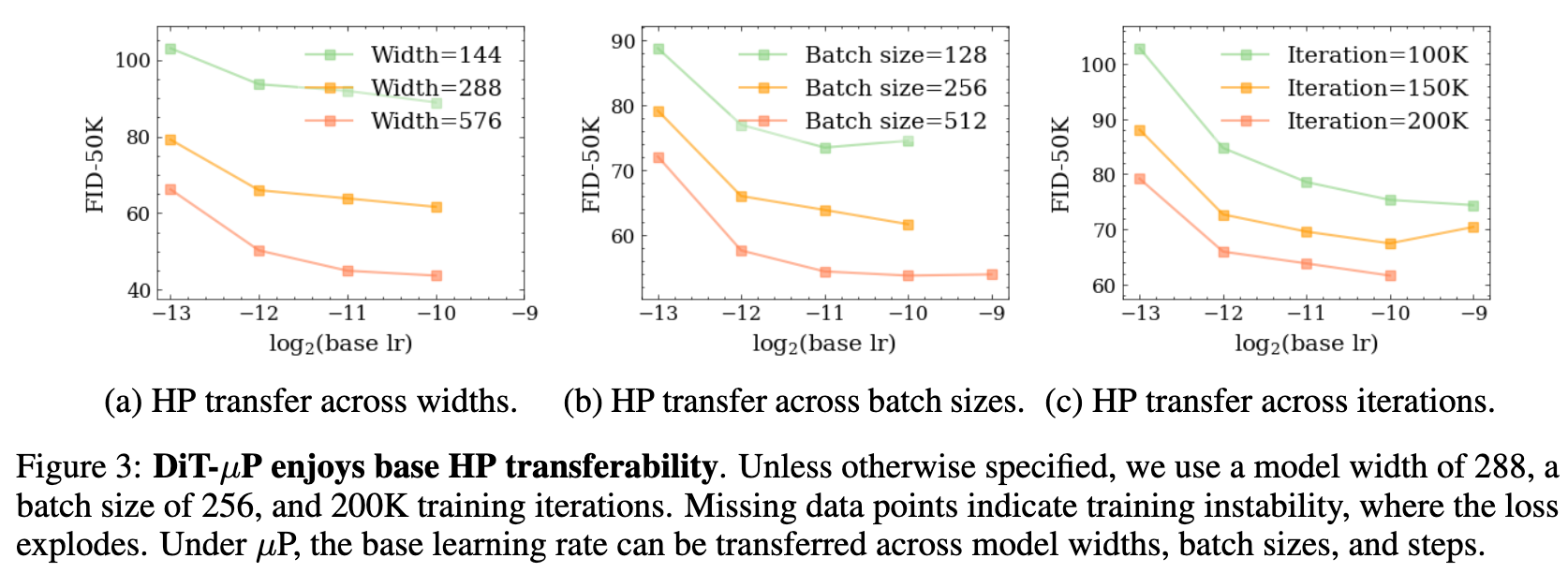
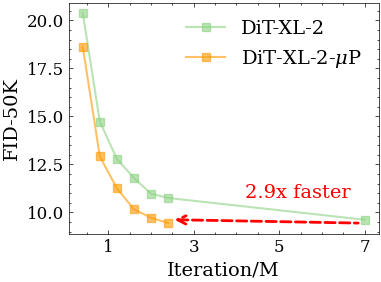
We systematically demonstrate that DiT under μP enjoys robust HP transferability. Notably, DiT-XL-2-μP with transferred learning rate achieves 2.9 times faster convergence than the original DiT-XL-2.
We validate that diffusion Transformers under μP outperform their respective baselines while requiring small tuning cost (e.g., 3% FLOPs of human experts for MMDiT-18B).

In this repository, we provide the code and introduction to reproduce our experiments on DiT and PixArt-α. Our setup and codebase follow the remarkable DiT, PixArt-α and Maximal Update Parametrization (μP).

Systematic investigation for DiT-μP on ImageNet

Implementation of DiT-μP

We implement DiT-μP based on the original codebase. We just need to adjust the weight multiplier and variance of each weight at initalization according to the μP theory. We then use the MuAdamW optimizer from the original codebase to adjust learning rate of each weight at training. Our modifications compared to the original DiT are marked with "# mup" in the code.

We use the coord_check method to verify the correctness of DiT-μP. In the following figure, all curves stay horizontal, indicating that μP is implemented correctly.

python coordcheck.py --load_base_shapes width288_d28.bsh

HP transferability

We verify that DiT under μP enjoys robust HP transferability as the following figures (Figure 3 in our paper).

We describe how to reproduce Figure 3(a) in our paper.

First, we need to train some DiTs with different widths and learning rates under μP.

cd DiT/
torchrun --master_port=${MASTER_PORT} \
--master_addr=${MASTER_ADDR} \
--nproc_per_node=8 \ #A100-80G GPU
--nnodes=1 \
--node_rank=${NODE_RANK} \
train_mup.py \
--load_base_shapes width288_d28.bsh \
--mup \
--global_batch_size 256 \
--num_heads 4 \ # {2, 4, 8}
--epochs 40 \
--loglr -10 # {-9, -10, -11, -12, -13}

Second, we sample 50K images from these trained DiTs.

cd DiT
torchrun --master_port=${MASTER_PORT} \
--master_addr=${MASTER_ADDR} \
--nproc_per_node=8 \ # A100-80G or V100-32G
--nnodes=1 \
--node_rank=${NODE_RANK} \
sample_ddp.py \
--load_base_shapes width288_d28.bsh \
--mup \
--num_heads 4 \ # {2, 4, 8}
--ckpt path_ckpt.pth \
--cfg_scale 1 \
--vae mse

Third, we evaluate the performance (e.g., FID, IS, sFID) of these DiTs based on the ADM codebase.

cd DiT
python create_npz.py # get sampled_50K_images.npz
python evaluator.py \
--ref_batch path/VIRTUAL_imagenet256_labeled.npz \
--sample_batch sampled_50K_images.npz

Finally, we can plot the figures with these data.

Pretrain DiT-XL-2-μP

The best learning rate searched in small models is $2^{-10}$, we then use it to pretrain the DiT-XL-2-μP.

cd DiT/
torchrun --master_port=${MASTER_PORT} \
--master_addr=${MASTER_ADDR} \
--nproc_per_node=8 \ # A100-80G
--nnodes=4 \
--node_rank=${NODE_RANK} \
train_mup.py \
--load_base_shapes width288_d28.bsh \
--mup \
--global_batch_size 256 \
--num_heads 16 \
--epochs 480 \
--loglr -10

To reproduce the original DiT-XL-2 pretraining, we can run

cd DiT/
torchrun --master_port=${MASTER_PORT} \
--master_addr=${MASTER_ADDR} \
--nproc_per_node=8 \ # A100-80G
--nnodes=4 \
--node_rank=${NODE_RANK} \
train_mup.py \
--global_batch_size 256 \
--num_heads 16 \
--epochs 1400

The sampling and evaluation are the same as before.

Scaling PixArt-α-μP on SA-1B

Dataset

We use the SA-1B/SAM dataset following the instructions in PixArt-α repo.

Implementation of PixArt-α-μP

Our modifications on initialization compared with the original PixArt-α are marked with "# mup" in the code. It correctness can also be verified by the coord_check method.

python scripts/coordcheck.py \
--load_base_shapes L28_width288.bsh \
--config configs/pixart_config/PixArt_mup_img256_SAM_coord.py \
--work_dir output/pixelart_coordcheck

HP search on proxy models

To reproduce the results of base learning rate search on PixArt-α-μP proxy tasks (Table 2 in our paper), we run

cd PixArt-alpha-master/
torchrun --master_port=${MASTER_PORT} \
--master_addr=${MASTER_ADDR} \
--nproc_per_node=8 \ # A100-80G
--nnodes=1 \
--node_rank=${NODE_RANK} \
train_scripts/train.py \
--config configs/pixart_config/PixArt_mup_xl2_img256_SAM_proxy.py \
--work-dir output/search_SAM_256/loglr-10 \
--load_base_shapes L28_width288.bsh \
--loglr -10 # {-9, -10, -11, -12, -13}

Pretrain PixArt-α-μP

We use the best base learning rate $2^{-10}$ to train the PixArt-α-μP.

cd PixArt-alpha-master/
torchrun --master_port=${MASTER_PORT} \
--master_addr=${MASTER_ADDR} \
--nproc_per_node=8 \ # A100-80G
--nnodes=4 \
--node_rank=${NODE_RANK} \
train_scripts/train.py \
--config configs/pixart_config/PixArt_mup_xl2_img256_SAM_target.py \
--work-dir output/pretrain_SAM_256_mup/loglr-10 \
--load_base_shapes L28_width288.bsh

To train the original PixArt-α, we can run

cd PixArt-alpha-master/
torchrun --master_port=${MASTER_PORT} \
--master_addr=${MASTER_ADDR} \
--nproc_per_node=8 \ # A100-80G
--nnodes=4 \
--node_rank=${NODE_RANK} \
train_scripts/train.py \
--config configs/pixart_config/PixArt_xl2_img256_SAM.py \
--work-dir output/train_SAM_256

Evaluation

MS-COCO and MJHQ

First, to obtain FID and CLIP score on MS-COCO and MJHQ-30K dataset, we need to generate images with their prompts

python scripts/inference.py \
--config config_path.py \
--load_base_shapes L28_width288.bsh \
--model_path ckpt_path.pth \
--dataset mjhq # or mscoco

Second, the FID of two given image sets can be calculated by

python tools/fid.py \
--ref_dir data/mjhq/imgs \
--fake_dir sampled_imgs

Third, to obtain the CLIP score of sampled images, we can run

python tools/clip_score.py \
--image_dir sampled_imgs \
--save_path result.csv

GenEval

First, generate images with the prompts from GenEval

python scripts/inference_geneval.py \
--config config_path.py \
--load_base_shapes L28_width288.bsh \
--model_path ckpt_path.pth

Second, obtain the score

python tools/evaluate_geneval.py \
--imagedir sampled_imgs \
--outfile sampled_imgs.jsonl \
--model-path output/pretrained_models/mask2former

python tools/summary_scores.py sampled_imgs.jsonl

Acknowledgement

This project is heavily based on the remarkable DiT, PixArt-α and Maximal Update Parametrization (μP). Thanks for their great work!

Citation

If our paper "Scaling Diffusion Transformers Efficiently via μP" or this repository was useful to you, please cite:

ML-GSAI/Scaling-Diffusion-Transformers-muP