A THEory LEarning MAchine for grammar induction.
THELEMA is an inductive logic programming algorithm and a program based on that algorithm. The algorithm learns a graph structure from sequential data, for instance a grammar from examples of sentences in a tagret language.
For the time being THELEMA is taking its first baby steps in its very own blocks world: the Controlled Natural Language at the heart of the Collectible Card Game Magic: the Gathering known as "Ability Text" (no affiliation between this project and the publishers of that game).
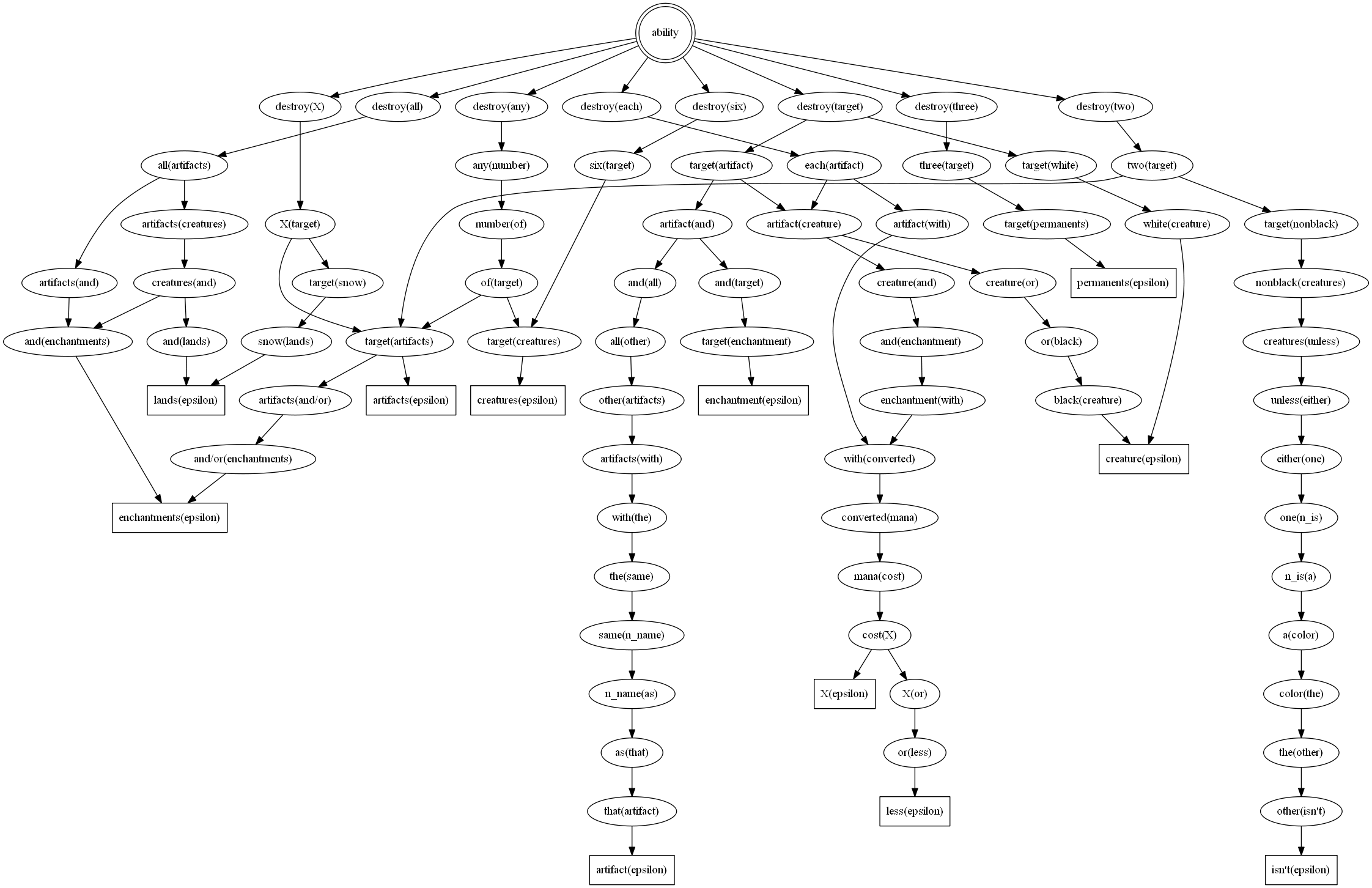
Here is a diagram of a grammar THELEMA learned from a small set of 18 examples of Ability Text:
THELEMA is written in Prolog. You will need to have Swi-Prolog 7.0 to 7.3.13 installed on your system.
I repeat: you need a version of Swi Prolog between 7.0 and 7.3.13 to run THELEMA. If you have a newer version, you 'll have to exit the Swi Prolog top-level and reload the project every time you make a configuration change. Earlier versions of Swi had a bug that I unwittingly exploited (or so it seems), it was fixed in v 7.3.15 or 3.14 and I have to update my code- but until then, make sure you have the right version of Swi. Earlier versions are right out of the question also- 7.x is to Swi what 3.4 is to Python. Except Swi 7.x rocks.
Start THELEMA by loading the file:
tree_learning/load_tree_learning.pl
On a windows machine you can double-click the file and it will open the Prolog console and the Swi-Prolog IDE. On Linux:
- change directory to tree_learning
- start Swi-Prolog, and
- enter "[load_tree_learning]."
On Linux that will probably not bring up the IDE. But you never know.
To begin training THELEMA you need to edit the configuration file:
tree_learning/configuration.pl
You should read the comments in that file. They will probably make sense after a while. To begin with, make sure you have the following options set:
examples_file_name(examples_mtg_hand_simulation).
language_file_name(language_mtg_hand_simulation).
lexicalisation_strategy(none).
output_type(dcg).
production_augmentation(greibach).
production_composition(synonym).
rename_built_ins(n_).
If you need to change a setting, remember to enter:
make.
At the Prolog top-level, or the changes won't take.
With these settings, THELEMA will learn a non-lexicalised Context-Free Grammar from the "examples_mtg_hand_simulation" mini-corpus (as its name implies this corpus was used for hand-simulations which explains why it's so tiny).
Start training by entering this query at the Prolog top-level:
print_grammar.
THELEMA will place a grammar file in tree_learning/output/ named after the configured examples and language file so that you can easily identify it.
THELEMA's "native" grammar format is Prolog's Definite Clause Grammars notation. DCGs have a direct translation to Horn Clauses so in most Prologs and indeed in Swi-Prolog, DCG rules will automatically compile to ordinary Prolog predicates when you load their source file. This might sound like a load of jargon but the upshot of this is that the grammar that THELEMA learns is really a program in Prolog. In fact, it's a parser and also generator for strings in the language described by the grammar.
You can verify this if by doing the following:
- Load the output grammar file from the Shiny Happy Path section into a new Prolog instance (don't use the old one or you'll get told off)
- Enter this query at the Prolog top-level:
forall(phrase(ability, P), writeln(P)).
If you followed the Shiny Happy Path to the letter, the above query should give you a set of nice little derivations reproducing the examples in the training corpus and even generalising a little.
If you didn't follow the Shiny Happy Path then woe is you. Larger datasets tend to produce grammars with recursive paths running though them. If you try to geneate new text from such a grammar Prolog will lock. If... when that happens you can abort execution with "Ctrl + C" and then "a", or by killing the Prolog instance.
You can also use the induced grammar as a recogniser, to accept or reject strings.
Try this; at the Prolog top-level, on the same instance where you loaded the output of the Shiny Happy Path, enter the following queries:
phrase(ability, [destroy,target,artifact]).
phrase(ability, [destroy,target,X]).
phrase(ability, [destroy,target,stassa]).
The first query should say "true" and then wait for input. Press "enter" to end the search for more answers (if you press ";" the query exits with "false" because it can't find more results that match its pattern).
The second query should bind "X" to "artifact" and wait for input. Press ";" or the space bar for more results and "X" will bind to "creature". Press enter to end the search or ";" to see the "false".
The third query lived in a house of stone. There is no such derivation possible in the grammar you loaded, therefore Prolog will immediately say "false" and end its search for answers. In any case, you should never destroy stassas, they don't like that. They do like chocolate, however. Do you have chocolate? If you have chocolate then you can proceed to the next section.
For now, THELEMA only learns one type of grammar, a determinstic Context-Free Grammar in a restricted Greibach Normal Form, where all rules are of the form:
a → aA
In other words, a single terminal followed by a single nonterminal. Note that the single terminal is always the synonym of the production's left-hand side; essentially the solitary terminal is a label annotating the node on the retrieved graph that the production represents. A non-restricted form of GNF and possibly other grammar formalisms will follow in the future.
The fact that THELEMA models its input as a grammar is a happy coincidence. It's trivial to represent a context-free grammar as a graph with arcs mapping the relations between nonterminals.
To see this in action, set the following option in configuration.pl:
output_type(lean_dot).
Then train THELEMA with "print_grammar" as above. THELEMA will then print out its induced grammar in the dot-language format used for visualisation (the file is still placed in tree_learning/output). You can feed that file directly into a visualisation package such as Graphviz to generate a diagram of the induced grammar. This is how the image at the start of this file was created.
With a bit of elbow grease you can even visualise a grammar as a network by exporting it into a package like Gephi or Cytoscape. See the image below for example, the visualisation of a grammar learned from 177 examples and rendered as a network diagram in Gephi:
THELEMA can also print out its grammar in the BNF and EBNF formats used in parser generators such as Yacc and Bison. Neither of these formats is particularly strictly implemented at this point, but you can always play around with them a bit and see if you can get them to work with your favourite compiler compiler.