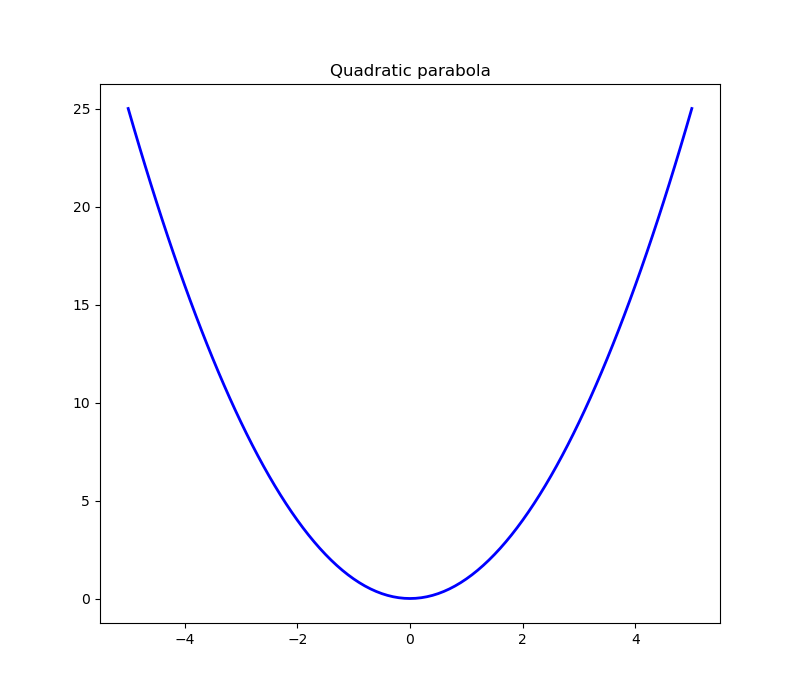
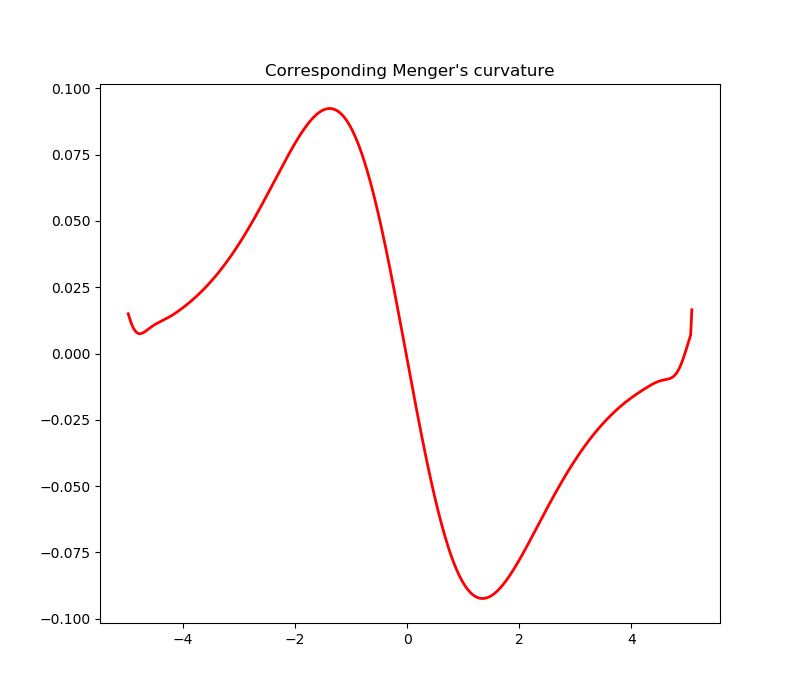
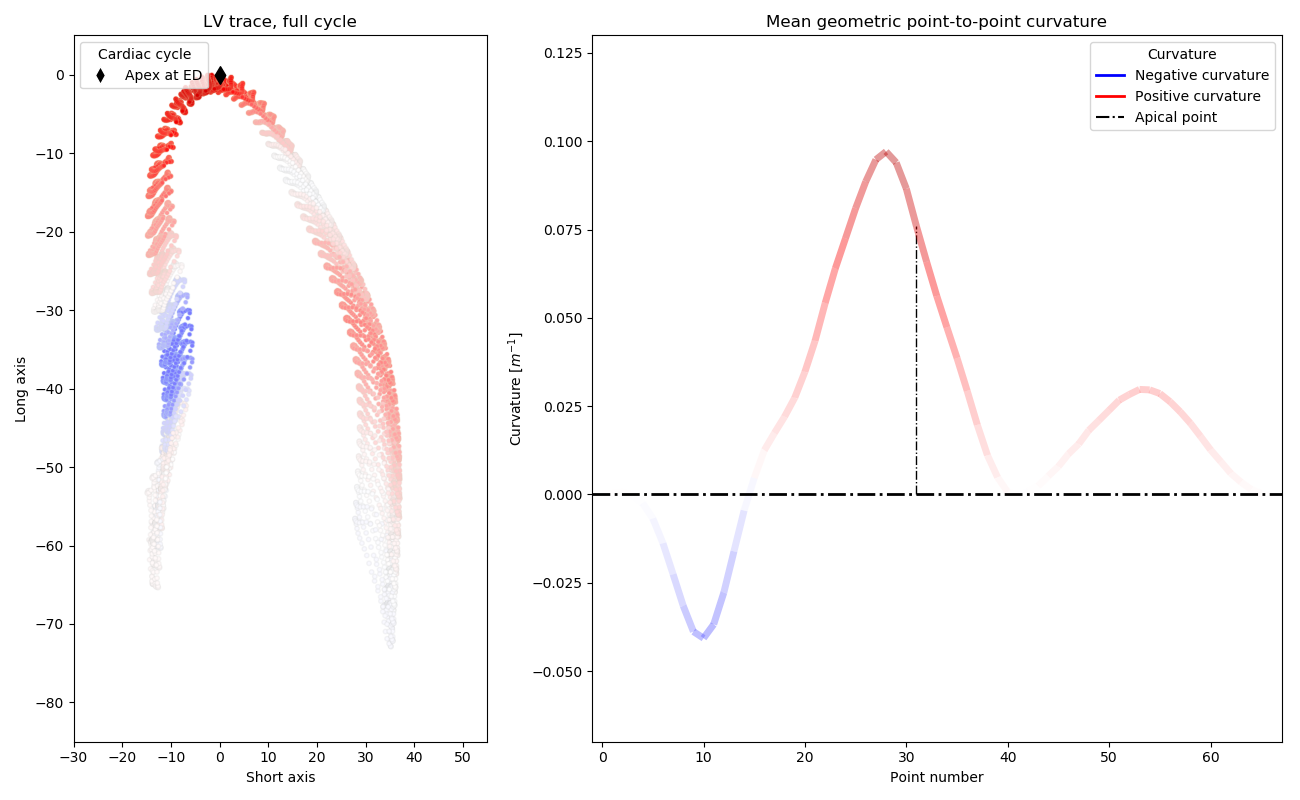
In mathematics, the Menger curvature of three points in n-dimensional Euclidean space is the reciprocal of the radius of the circle that passes through the three points. Intuitively, a curvature is the amount by which a geometric object deviates from being a straight line in case of the curve.
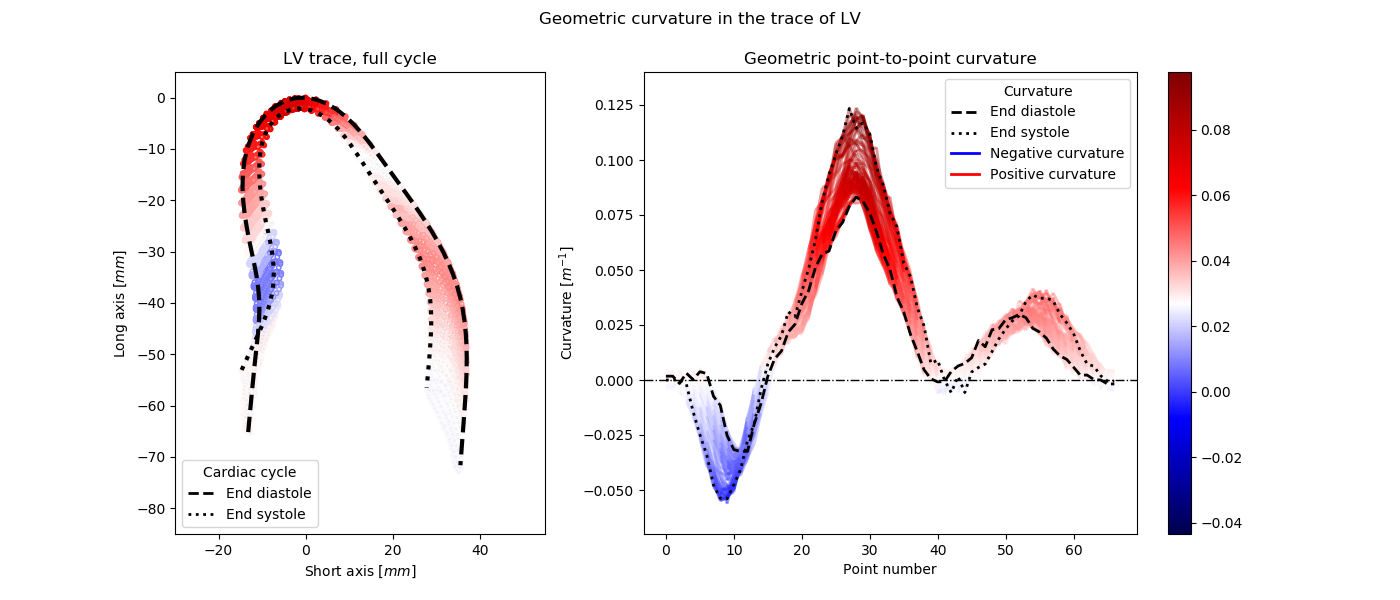
In this project, the curvature measurement is applied to human left ventricle traces, in order to determine the occurrence of the left ventricular basal septal hypertrophy from 2 dimensional echocardiography (2D echo). The described methods can be applied to any traces of the left ventricle.
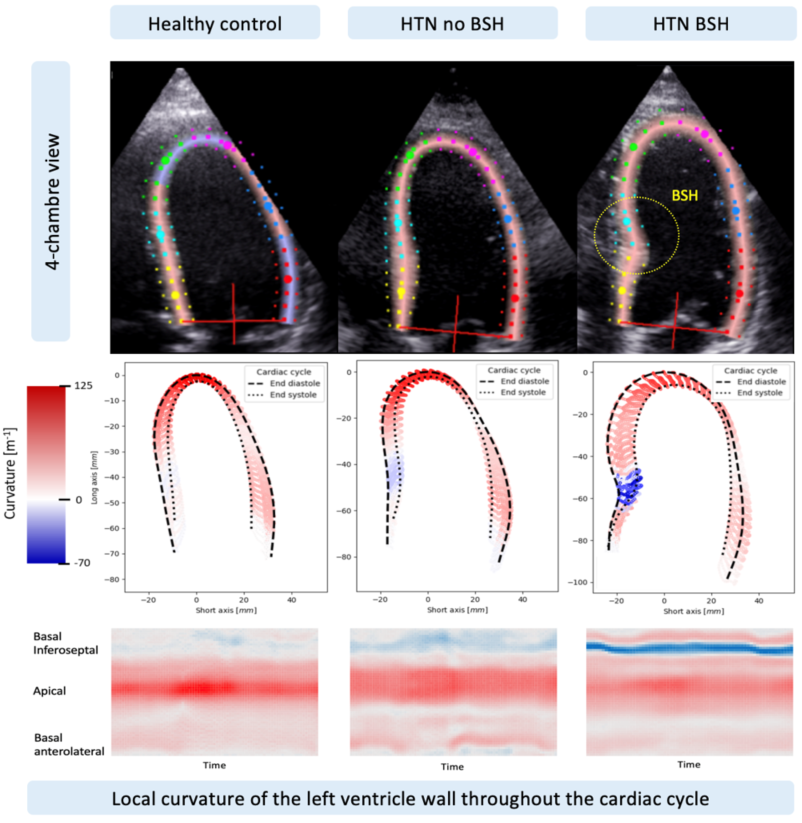
Localized basal septal hypertrophy (BSH) is a known marker of a more advanced impact of afterload on cardiac function in hypertension. There is variability in criteria used for defining BSH, mainly based on ratios of multiple septal wall thickness measurements with high inter-observer variability. The aim is to investigate septal curvature as a novel, semi-automated method for better recognition of patients with BSH.
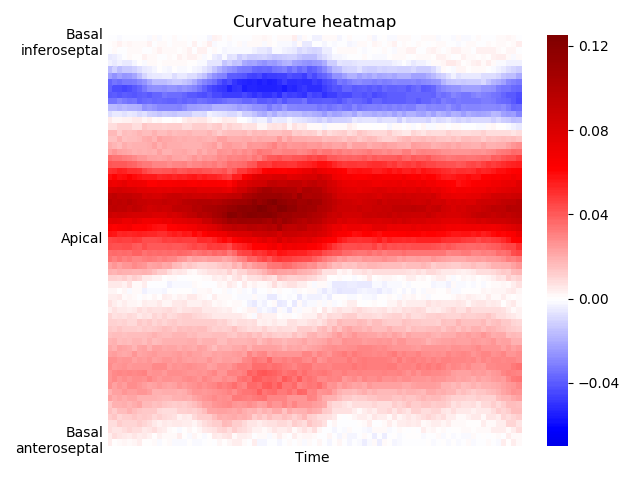
Examples of differences in septal curvature among 3 patients: healthy, hypertensive and hypertensive with septal bulge:
Please cite the following publication:
Marciniak M, Gilbert A, Loncaric F, Fernandes JF, Bijnens B, Sitges M, King A, Crispi F, Lamata P.
Septal curvature as a robust and reproducible marker for basal septal hypertrophy.
J Hypertens. 2021 Jul 1;39(7):1421-1428. doi: 10.1097/HJH.0000000000002813. PMID: 33534345; PMCID: PMC8183485.