/AC3-CPP-Crossword-Solver

C++ Crossword Solver using AC3 and Back Track Algorithms.

Primary LanguageC++

CPP-Crossword-Solver

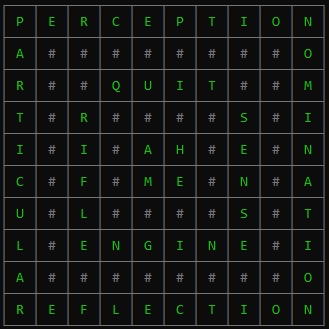
C++ Crossword Solver using AC-3 and BackTrack Algorithms.

AC-3

AC-3 (or Arc Consistency algorithm #3) is an algorithm that helps solving CSPs, its mechanism is simple and straitforward and as follow:

  • First, we have some variables and each variable has a domain and constraints.
  • There're arcs among variables.
  • Make sure that variable Vᵢ is Node-Consistent by satisfing the unary constraints Cᵢ.
  • Make sure that for each pair of variable Vᵢ, Vⱼ; Vᵢ is Arc-Consistent withVⱼ and satisfies all the constraints by removing values from the domain of Vᵢ which is unconsistent with Vⱼ.
  • After the removing all unconsistent values; if any domain is empty then no solution can be found.

Psuedo code:

Function revise(Vₓ, Vᵧ, Cₓᵧ):
    revised ← false
    for each x in Vₓ domain:
        if there's no y in Vᵧ domain satisfies constraints Cₓᵧ:
            Vₓ.remove(x)
            revised ← true
    return revised

Function AC3:
    S ← set of all (Vᵢ, Vⱼ, Cᵢⱼ) such that every pair of Vᵢ and Vⱼ has a constraint Cᵢⱼ
    While S is not empty:
        select X, Y, C from S
        remove X, Y, C from S
        if revise(X, Y, C):
            if domain of X is empty:
                return false
            for each K in Vₖ:
                S.add(X, K, Cₓₖ)
    return true

BackTrack

BackTrack is just a spicy recursion used for solving CSPs that incrementally builds candidates to the solutions, and abandons a candidate (backtracks) as soon as it determines that the candidate cannot possibly be completed to a valid solution.

Psuedo code:

Function BackTrack(assigment, CSP):
    if assigment is complete:
        return true
    Vₓ ← select_unassigned_variable(CSP)
    for each val in order_domain_values(Vₓ, assigment, CSP):
        if adding Vₓ = val satisfies constraints Cₓ:
            assigment.add(Vₓ = val)
            result ← BackTrack(assigment, CSP)
            if result:
                return true
        remove Vₓ = val
    return false

Code Logic and Walkthrough

Project has three main files:

1. VARIABLES.h

contains two classes:

  • CELL is just customized std::pair clone to store start point coordinates and overlapping between two variables where overlap.x is the index of the overlapping character for left variable and overlap.y for the right one.
  • VARIABLE is just a structure to represent the empty place of a word in crossword which stores its starting point, length, direction and the content of the word.

2. crossword.h

contains definition of the crossword class (its variables, crossword structure or board and domain of words that each variable can have), declaring some prototypes to be implemented in crossword.cpp and implementing input and output stuff.

3. crossword.cpp

which is the core of the project we can devide this file to 4 main parts:

  • Tokenization and variables extraction (via VARIABLE_tokenize, extract_VARIABLES) we just iterate over the crossword's board and extract the empty chuncks.
  • Filtering domain of words (setVARIABLES_domains) to fit into each variable by ensuring that the word must have the same length as variable which is our unary constraint.
  • Applying AC3 by selecting all pair of variables that have an arc between each pair of them and complete the process of AC-3 which I dicussed before.
  • Finaly, the BackTrack: select an unassigned variable (via select_unassigned_VARIABLE), then sort the domain of the selected variable from the least eliminating values word to the most eliminating one (via order_domain_values). Next, try setting every word in that domain by order if the current word is making the variable in Arc-consistent with all assigned overlapping variables continue the process to all variables (via consistent_for_assigned_vars) untill the crossword is complete and all variables are assigned (via is_complete).

4. Beside driver one runner.cpp which load crossword structure and words to solve and print.

Code run

After compiling files (for Ex.: g++ runner.cpp crossword.cpp -o crossword) and run exe file:

  • For simple.txt (.\crossword 10 CrosswordBoards\simple.txt Words\Top3000EnglishWords.txt) you will be able to see:

  • For medium.txt (.\crossword 10 CrosswordBoards\medium.txt Words\Top3000EnglishWords.txt) you will be able to see:

  • For complex.txt (.\crossword 20 CrosswordBoards\complex.txt Words\Top3000EnglishWords.txt) you will be able to see:

Glossary:

Variable

can be defined as a symbol or placeholder to represent some value (such X, Y, ..etc) and has a domain which is a set of possible values that a variable can hold.

Arc

Arc or edge can be defined as a connection among variables which descripe the relation between two variables.

Arc-Consistency

Variable X is Arc-consistent with variable Y only if all constraints {Cᵢ, Cᵢ₊₁,.., Cⱼ} involving X and Y are satisfied.

Node-Consistency

Variable X is Node-consistent only if it satisfies all constraints {Cᵢ, Cᵢ₊₁,.., Cⱼ} involving variable X.

Constraint

can be defined as a relation that limits the values a variable may have. Constraints can be unary (or node-consistency descripes the limitations and values that a variable can have), binary (or arc-consistency descripes the realation between two variables) or more. Ex.: let V₀ and V₁ be variables and their domains are {-2, -3, 3, 0, 6, 5} and {6, 11, 3, 12, 2, 5} respectively. Let constraints C₀ = "variables must be greater than 2" and C₁ = "V₀ + V₁ must be greater than or equal to 17". According to unary constraint C₀: domain of V₀ = {3, 6, 5} and V₁ = {6, 11, 3, 12, 5} to achieve Node-consistency, and for binary constraint C₁: V₀ = {6, 5} and V₁ = {11, 12} to achieve Arc-consistency.

CSP

(Constraint Satisfaction Problem) is defined as a triple {X, D, C} Where X = {X₁, X₂,..., Xₙ₋₁, Xₙ} is a set of variables, D = {D₁, D₂,..., Dₙ₋₁, Dₙ} is a set of values dmains respective to variables and C = {C₁, C₂,..., Cₘ₋₁, Cₘ} is a set of constraints. Each variable Xᵢ has a domain of values Dᵢ and each constraint Cᵢ limits the domain of one variable or more. CSP can be solved only if every Dᵢ is not empty and Xᵢ satisfies all the constraints {Cⱼ, Cⱼ₊₁,.., Cₖ} where each constraint involving variable Xᵢ.