Linear Regression for Predicting Student Percentage

This GitHub repository contains Python code for a simple linear regression model that predicts a student's percentage based on the number of study hours. This is a basic machine learning project that demonstrates the fundamental concepts of linear regression and can serve as a starting point for more complex regression tasks.

Introduction
Dependencies
Usage
Data
Results

Introduction

Linear regression is a statistical method used for modeling the relationship between a dependent variable (in this case, the student's percentage) and one or more independent variables (in this case, the number of study hours). The goal is to find a linear relationship that can predict the dependent variable based on the independent variable(s).

In this repository, we provide a Python script that demonstrates how to perform linear regression to predict a student's percentage based on their study hours.

Dependencies

To run the code in this repository, you will need the following dependencies:

Python (>=3.6)
Pandas
Matplotlib
Scikit-Learn (sklearn)

Usage

Clone the repository to your local machine:

git clone https://github.com/MahmoudMansour27/Linear_regression-Std-Per-hours.git

Navigate to the project directory:
```
cd Linear_regression-Std-Per-hours
```
Run the Linear regression model.py script:
```
python Linear regression model.py
```

Data

The dataset used in this project is provided in the Student data.csv file. This file contains two columns: "Hours" (the number of study hours) and "Scores" (the corresponding student scores). You can replace this dataset with your own data if needed.

Results

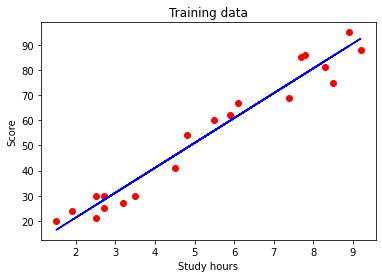
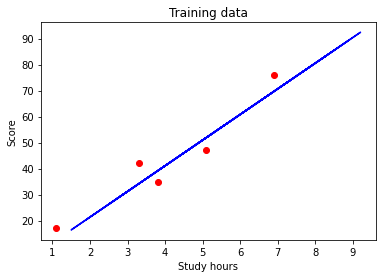
After running the script, you will see a scatter plot of the data points along with the linear regression line.

Train set visualisation
Test set visualisation

The script will also display the coefficient, intercept, and the R-squared value, which measures the goodness of fit of the model.