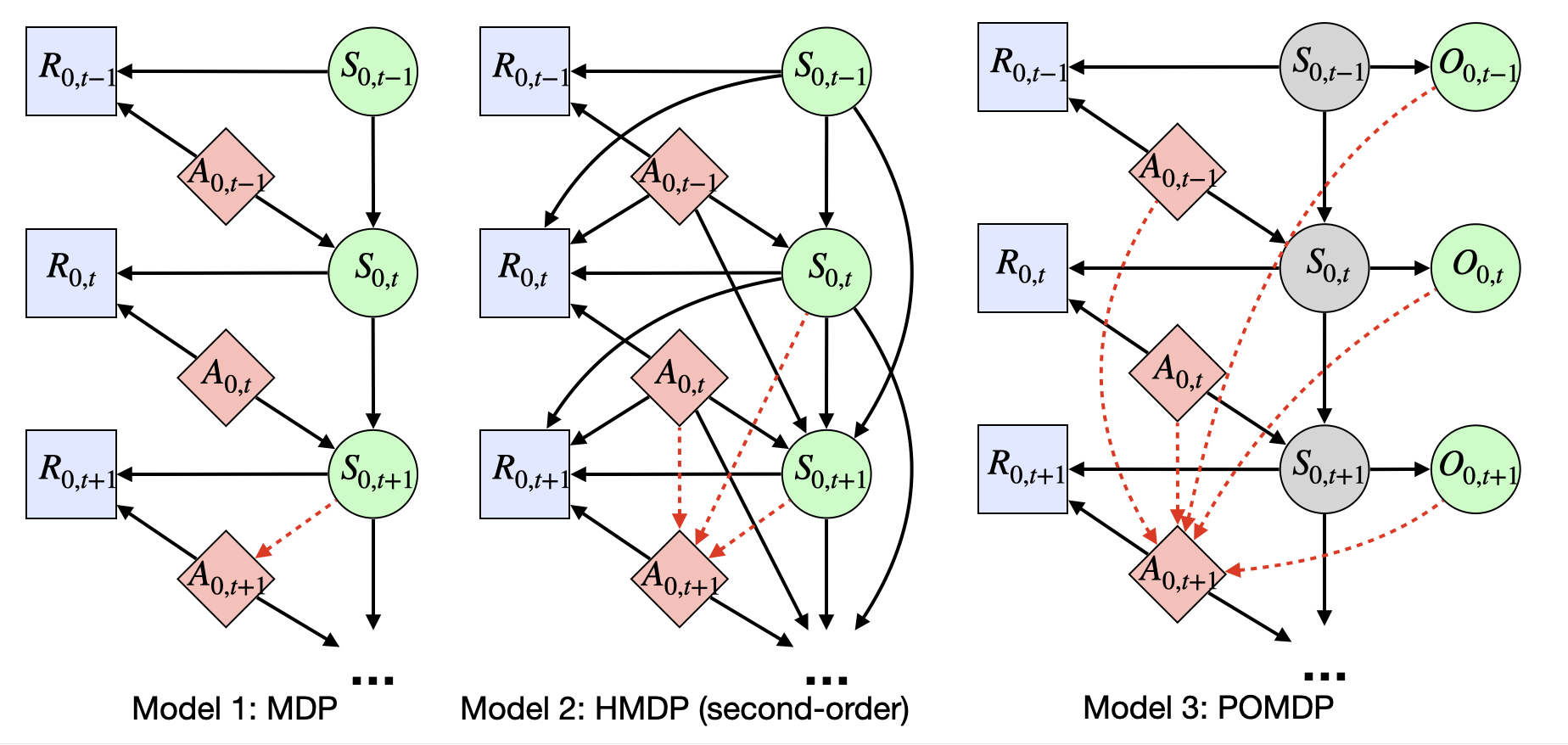
Does the Markov Decision Process Fit the Data: Testing for the Markov Property in Sequential Decision Making
This repository contains the implementation for the paper "Does the Markov Decision Process Fit the Data: Testing for the Markov Property in Sequential Decision Making" (ICML 2020) in Python.
The Markov assumption (MA) is fundamental to the empirical validity of reinforcement learning. In this paper, we propose a novel Forward-Backward Learning procedure to test MA in sequential decision making. The proposed test does not assume any parametric form on the joint distribution of the observed data and plays an important role for identifying the optimal policy in high-order Markov decision processes and partially observable MDPs. We apply our test to both synthetic datasets and a real data example from mobile health studies to illustrate its usefulness.
Change your working directory to this main folder, run conda env create --file TestMDP.yml to create the Conda environment, and then run conda activate TestMDP to activate the environment.
/test_func: main functions for the proposed test_core_test_fun.py: main functions for the proposed test, including Algorithm 1 and 2 in the paper, and their componnets._QRF.py: the random forests regressor used in our experiments._uti_basic.pyand_utility.py: helper functions
/experiment_script: scripts for reproducing results. See next section./experiment_func: supporting functions for the experiments presented in the paper: 2._DGP_Ohio.py: simulate data and evaluate policies for the HMDP synthetic data section. 3._DGP_TIGER.py: simulate data for the POMDP synthetic data section. 7._utility_RL.py: RL algorithms used in the experiments, including FQI, FQE and related functions.
Simply run the corresponding scripts:
- Figure 2:
Ohio_simu_testing.py - Figure 3:
Ohio_simu_values.pyandOhio_simu_seq_lags.py - Figure 4:
Tiger_simu.py
- run
from _core_test_fun import *to import required functions - Algorithm 1: decide whether or not your data satisfies J-th order Markov property
- make sure your data, the observed trajectories, is a list of [X, A], each for one trajectory. Here, X is a T by dim_state_variable array for observed states, and A is a T by dim_action_variable array for observed actions.
- run
test(data = data, J = J), and the output is the p-value. More optional parameters can be found in the file.
- Algorithm 2: decide whether the system is an MDP (and its order) or the system is most likely to be a POMDP
- make sure your data and parameters satisfy the requirement for
test(). - specify the significance level alpha and order upper bound K.
- run
selectOrder(data = data, K = K, alpha = alpha). More optional parameters can be found in the file.
- make sure your data and parameters satisfy the requirement for
Please cite our paper Does the Markov Decision Process Fit the Data: Testing for the Markov Property in Sequential Decision Making (ICML 2020)
@inproceedings{shi2020does,
title={Does the Markov decision process fit the data: testing for the Markov property in sequential decision making},
author={Shi, Chengchun and Wan, Runzhe and Song, Rui and Lu, Wenbin and Leng, Ling},
booktitle={International Conference on Machine Learning},
pages={8807--8817},
year={2020},
organization={PMLR}
}
All contributions welcome! All content in this repository is licensed under the MIT license.