Link to Udacity project proposal: https://docs.google.com/document/d/1ycGeb1QYKATG6jvz74SAMqxrlek9Ed4RYrzWNhWS-0Q/pub
This project contains a Flask Web-App which allows the user to predict future asset prices. The user can create a model by choosing the tickers and the time range which should be used to train a machine learning model in the background. Afterwards, specific (future) dates can be selected and the price for one or multiple of the assets from the training set can be predicted. Models are automatically stored and can be deleted, if they are no longer required. Additionally, the user can add new tickers from NASDAQ, if the price data is available at Yahoo Finance. Tickers and their linked price data can also be deleted. The price and trade volume data for the tickers is stored in a background database, so that training can be done offline and without a requirement to download the data every time. The price data can also be updated to include the latest available prices.
The following Python libraries need to be installed:
- flask
- Flask-SocketIO
- jinja2
- flask_wtf
- wtforms
- flask-datepicker
- tensorflow
- keras
- joblib
- pandas_datareader
- sqlalchemy
- matplotlib
- sklearn
- scikeras
The application is written using the Python web framework Flask. Additionally, Tensorflow and Keras are used for training the machine learning models and Sqlalchemy is used to manage the database for storing the required data. The file app.py contains the main code which controls the program flow and the different flask web pages. The following steps need to be performed to run the application in Flask development mode:
Activate flask development environment:
export FLASK_ENV=development
Run the flask application
flask run
Additionally, here you can find an overview of the remaining files and folders in the repository:
./data_api: Classes and functions to access the Yahoo Finance API, the SQLite database and the SQLAlchemy database access framework. Here you can find a definition of the database scheme used in the background as well as different methods to send high level commands to the database (like initializing or updating the whole database) or low level commands to add, delete or edit entries.
./models: Classes and functions which are required to use machine learning models for price data prediction as well as functions to preprocess the data.
./templates: Templates for the web pages. These templates get loaded from the flask application and content gets filled in dynamically with jinja.
./data: This directory gets automatically created when you start using the application to store the database, as well as models and required scaler objects to the disk.
helper_functions.py: This file contains some helper functions to read and write data to the disk.
modelling_tests.ipynb and run_notebook.py: Used for performing GridSearch and to test model training. Not required for running the Flask App.
From the Yahoo Finance API, we get the 6 different values for each day. High price, low price, open price, close price, adjusted close price and volume. The 5 price data variables are all closely linked together, and only the adjusted close price reflects additional events like divident payouts or stock splits. Therefore, we only consider the adjusted close price (now referred to as "price") and the volume for our models.
Our goal is to predict future prices based on the past prices and the past volume. We can use the price/volume data of multiple stocks to predict the price/volume data of those multiple stocks to make use of the information hidden in the dependence of the development in those different assets. The problem is, that we have indeed a long timerange of past data, but we do not know anything about future prices (yet). Therefore, we need to split the past data into small sections and consider the earlier part of that section as the past data and the later part as the future. Therefore we can create many training sets of past/future data combinations to use for our training.
We need to define a useful metric or multiple metrics to evaluate the performance of our model and to compare different models with different hyperparameters. The goal of our model is to predict continious values, therefore we have a regression problem. For regression problems, we can use root mean squared error (RMSE) as a metric to optimize our model for. This metric weights larger deviations from the expected results more than lower deviations, but still has a value on the same scale as the output data.
- https://keras.io/api/metrics/
- https://machinelearningmastery.com/custom-metrics-deep-learning-keras-python/
When we check the data, we encounter one problem: We do not have price and volume data available for arbitrary dates for each asset. For weekends and holidays, there is usually no trading occuring on stock exchanges and therefore no price is determined. These dates without price data vary between different assets, depending on which exchanges they are listed and in which jurisdiction the exchanges are located. For some assets, like Bitcoin, there is nevertheless price data available for all days because there is less regulation about the exchanges and the cryptocurrencies can be easily traded completly digital. Additionally, there is no price data available before the asset was available. In the case of a publicly traded company, this is usually the IPO. To train a model with different assets, we are therefore likely facing missing values for some assets on some dates. For the first, problem, namely missing days for holidays/weekends, we have two options:
- Drop the data for a specific date, when no price data is missing for at least one asset
- Fill the missing prices with the average price of the days before and after
In the first case, we would potentially reduce our dataset significant, in case we have many different assets from many differen exchanges/jurisdictions. Therefore we take the second option and fill up the missing prices as mentioned.
To handle the second problem, namely missing asset prices because the asset was not publicly traded, it is more difficult to handle this. We can either:
- Limit the oldest date to the date when, the last asset was available
- Assume an average price of the asset for the time before it was available
- Assume a price of 0 before the asset was available
- Assume the price of the first day when the asset was available
We decide for the first option by simply again dropping the data rows if there are missing values.
To model our problem based on time series data, we need to recognize that the sequence of the data is also containing a lot of information and need to be used in the model. For this type of problem, a long short-term memory (LSTM) model is usually the best fit. With this model, the sequence data is processed in sequence and the data contained in the earlier sequence steps is kept during the whole process and has an influence on the prediction.
If we look at our training, data, we recognize different magnitudes especially when we compare the prices in dollars and the volume data in pieces. Additionally, the prices of stocks are also arbitrary, depending on how many single stock represent the ownership of the full company. Therefore we normalize the dataset to remove these huge ranges of values.
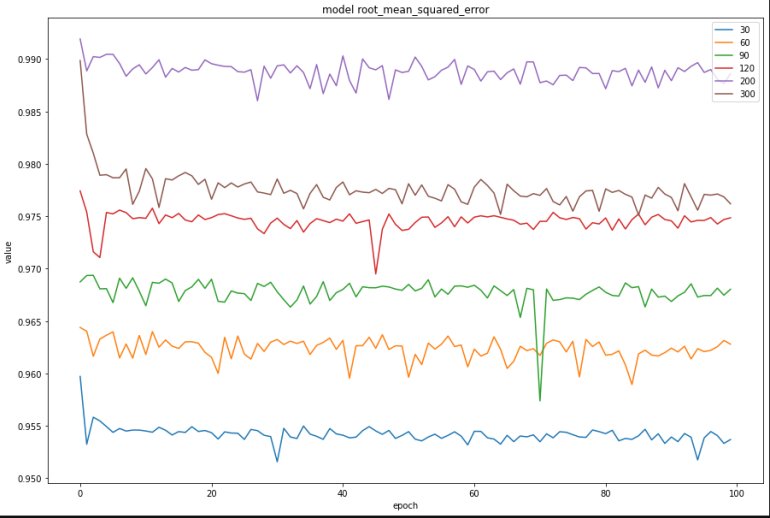
A further important aspect is to how precisely define our training data. What data should be the input for the output, and what should be the output. We take a amount of x consecutive days as the input and predict the data for the next day as the output. It needs to be determined, what is the optimal amount of days. After running several model instances with different values for x, we get the results shown in the diagram:
As we can see, we get the best results with x = 120 days.
Now that we have our dataset ready, we need to find out what is a good model to predict the data set for the next price based on the last 120 data sets. After trying out several amounts of layers, we conclude that having two layers with 32 and 32 nodes leads to a quite good result. We choose the adam optimizer because it is known to be a good and efficient optimizer for regression problems.
We can use GridSearchCV to further optimize our model. First, we check different combinations of batch_sizes and epochs to see which combinations leads to the best result.
To have more data for comparison, we run GridSearch with input data of a day_range x = 30 and x = 120:
| day range | 30 | 120 |
|---|---|---|
| epochs | 250 | 10 |
| batch_size | 32 | 64 |
Interestingly, if more days are used as input data, the batch size for training increases. On the other hand, the amount of epochs used to optimize the model is reduced tremendously. Only 10 epochs lead to the optimal solutiion (within our search space) compared to 250 epochs with an expected further slight improvement with additional epochs.
This reduction in epochs can be explained due to the fact that a higher number of epochs lead to the exploding gradient decent problem. This is a issue that is typical for regression models, because the output is not bounded and the combination of big weights and multiple layers can lead to very high gradients in the first layer, which lead to a nan value in out training metric. This can be overserved by checking the training logs which lead to non-useable models if many combinations with a high amount of epochs.
The best scores for out traning metric which we achied by tuning epochs and batch:size can be seen here:
| day_range | neg_root_mean_squared_error | root_mean_squared_error |
|---|---|---|
| 30 | -0.6563984733875825 | 0.6563984733875825 |
| 120 | -0.7624822584759838 | 0.7624822584759838 |
We also notice, that by just tuning batch_size and epochs, we get a better result for a data input day range of 30 days instead of 120 days.For 30 days, after running different combinations, we also realized that increasing the amount of epochs may improve the model a bit more, but it increases computation time extensively.
Furthermore, we can check different parameters for our adam activation function. The adam optimizer has several different parameters which we can test and combine to find a more optimal solution for our problem than with the default adam parameters.
| day_range | optimizer__amsgrad | optimizer__beta_1 | optimizer__beta_2 | optimizer__learning_rate |
|---|---|---|---|---|
| 30 | False | 0.8 | 0.89 | 0.01 |
| 120 | True | 0.9 | 0.89 | 0.1 |
This leads to the following results:
| day_range | neg_root_mean_squared_error | root_mean_squared_error |
|---|---|---|
| 30 | - 0.8073114933087524 | 0.8073114933087524 |
| 120 | -0.5844816053348458 | 0.5844816053348458 |
We can see that by tuning different parameters of the adam algorithm, we can optimize our 120-day model even better than our 30-days model.
After testing different LSTM networks, hyperparameters and training parameters either manually, or by the use of GridSearch, we can come to a conclusion for a quite good model:
- 120 days as input data to predict for day 121
- 2 LSTM layers with 32 nodes each
- Batch size for training of 64 and 10 training epochs
- Best parameters for the adam algorithm can be found in the section Hyperparameters for adam optimizer
Training machine learning models is a very time intensive process, if it is done wrong. Therefore I come to the following conclusions to speed up development in the future:
- Test all scripts etc. with small amounts of data to verify that everything runs correct to avoid breakages after hours of model training and grid search
- Catch errors and so that you code can finish to run without breaking
- Use Multithreading if possible
- Run scripts overnight to not waste time waiting for the result
- Run scripts on a server so that it can run without occuping local resources and wearing down a laptops CPU
There are possibilties to spend time and computation capacity to further improve the model. Furthermore, there are many more different optimizers as well as activation functions available, which have each individually countless different parameter combinations. These could be evaluated to see if there is a possibility to still improve the model. Also, other techniques except GridSearch could be used to test different sets of parameters. There is a library called RandomSearch which is similar to GridSearch, but creates more random combination by using ranges of values for the parameters. A different option woult be the usage of Genetic algorithms. These algorithms apply a model similar to evolution to the models to find a optimal set of parameters.
If the problem of exploding gradiends would be solved, then a training with additional epochs could be used to further improve the models. Details to that problem can be found here: https://stackoverflow.com/questions/37232782/nan-loss-when-training-regression-network
I want to express gratitudes for the team at Udacity which provides a great course on the topic of Data Science.
The code is available to anybody for personal and commercial use with the GNU General Public License v3.0. The used libraries may have there own different licences. I do not guarantee any correct functionality of the code. Use it at your own risk, no warranty is provided.