MartinCastroAlvarez/quantum-algorithms-java

Quantum Algorithms with Java

Quantum Computing

Quantum Algorithms with Java and Strange

References

• Strange
• StrangeFX
• Quantum Computing samples in Java
• How to Install Maven on Linux (Ubuntu)
• Quantum Logic Gate
• Quantum Key Distribution and BB84 Protocol
• Deutsch–Jozsa algorithm
• Grover's algorithm
• Shor's Algorithm

Instructions

Installing JDK on Linux

Downloading the JDK Binaries

wget https://download.java.net/java/GA/jdk13.0.1/cec27d702aa74d5a8630c65ae61e4305/9/GPL/openjdk-13.0.1_linux-x64_bin.tar.gz
tar -xvf openjdk-13.0.1_linux-x64_bin.tar.gz
sudo mv jdk-13.0.1 /opt/

Setting JAVA_HOME and Path Environment Variables

JAVA_HOME='/opt/jdk-13.0.1'
PATH="$JAVA_HOME/bin:$PATH"
export PATH

Verifing the Java Installation

java -version

Installing Maven on Linux

Downloading the Maven Binaries

wget https://mirrors.estointernet.in/apache/maven/maven-3/3.6.3/binaries/apache-maven-3.6.3-bin.tar.gz
tar -xvf apache-maven-3.6.3-bin.tar.gz
sudo mv apache-maven-3.6.3 /opt/

Setting M2_HOME and Path Variables

M2_HOME='/opt/apache-maven-3.6.3'
PATH="$M2_HOME/bin:$PATH"
export PATH

Verifing the Maven installation

mvn -version

Quantum Algorithms

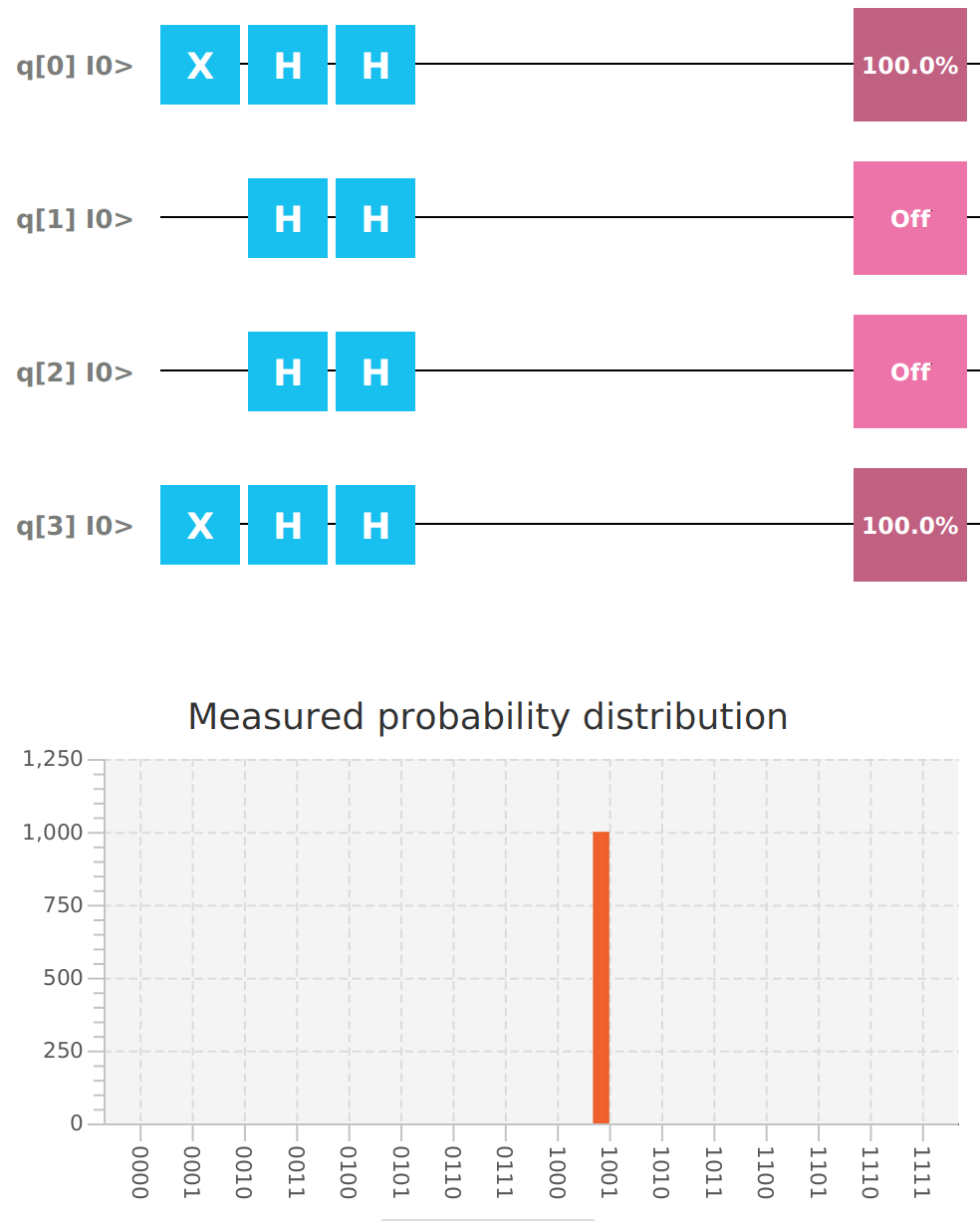
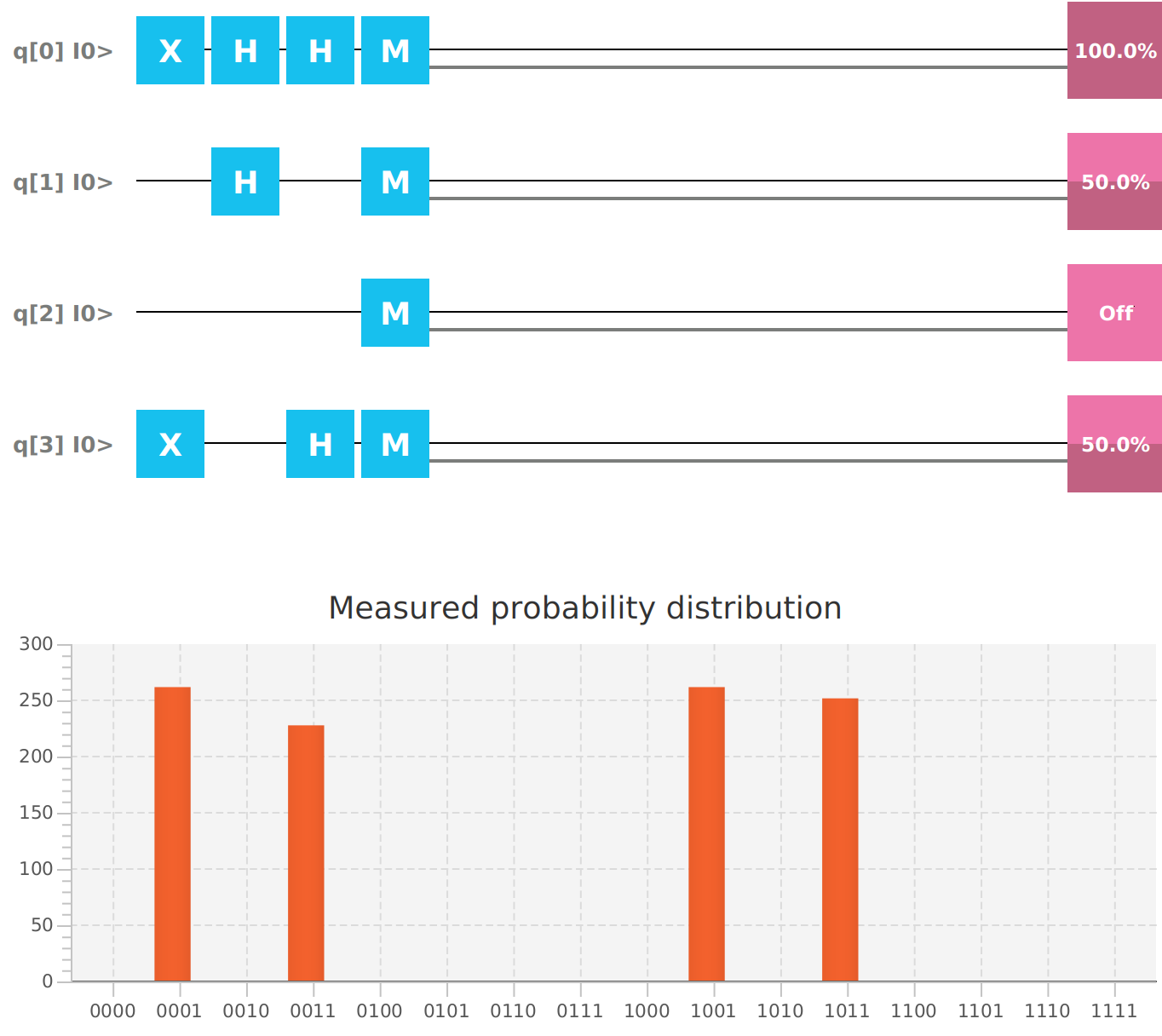
Quantum Superposition

Putting a Qubit into superposition using a Hadarmard gate.

mvn clean javafx:run --quiet --file superposition.xml

Qubit | Probability: 0.4999999701976776, Mesured: 0

Quantum Entanglement

Entangling 2 Qubits using a CNOT gate.

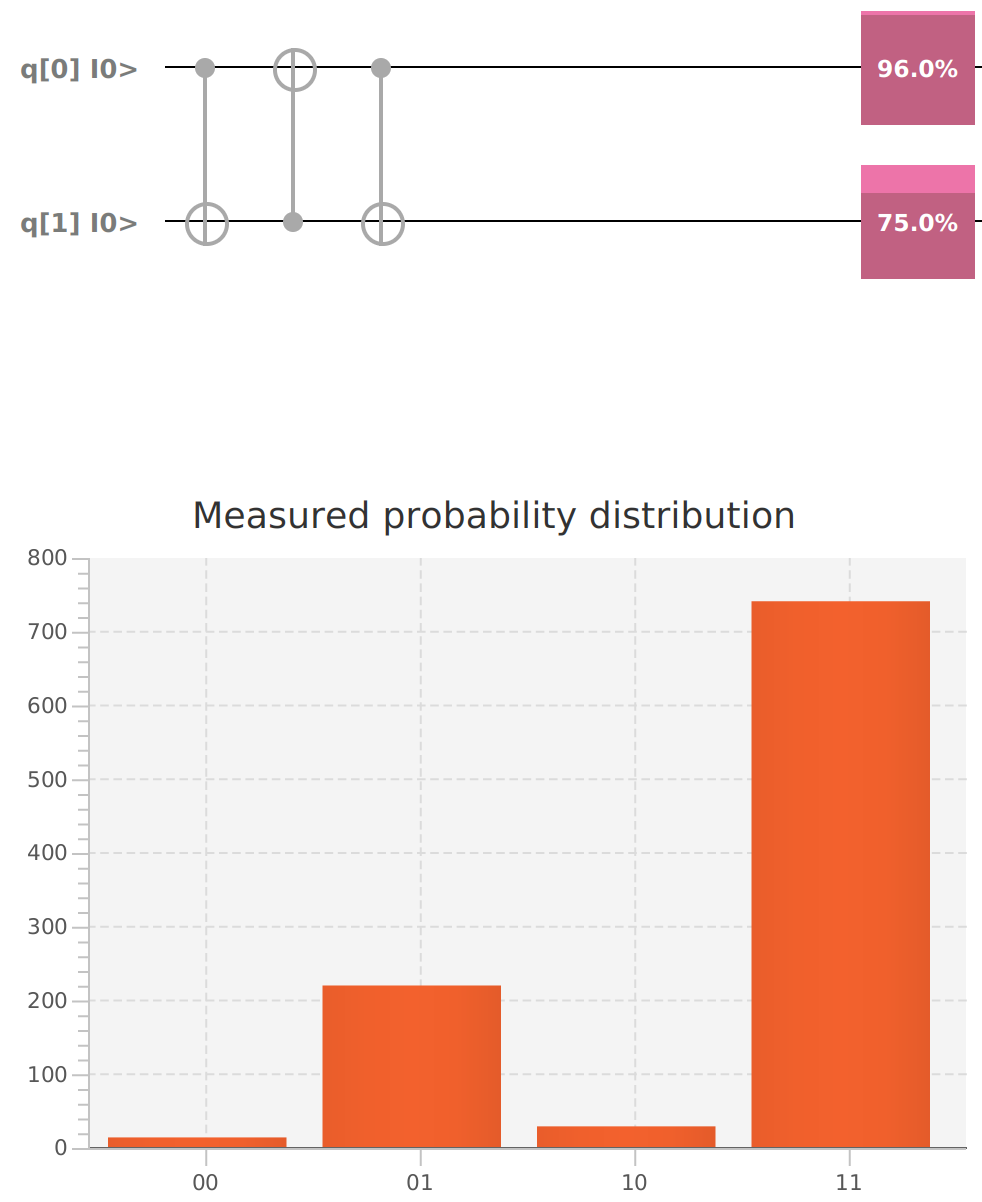
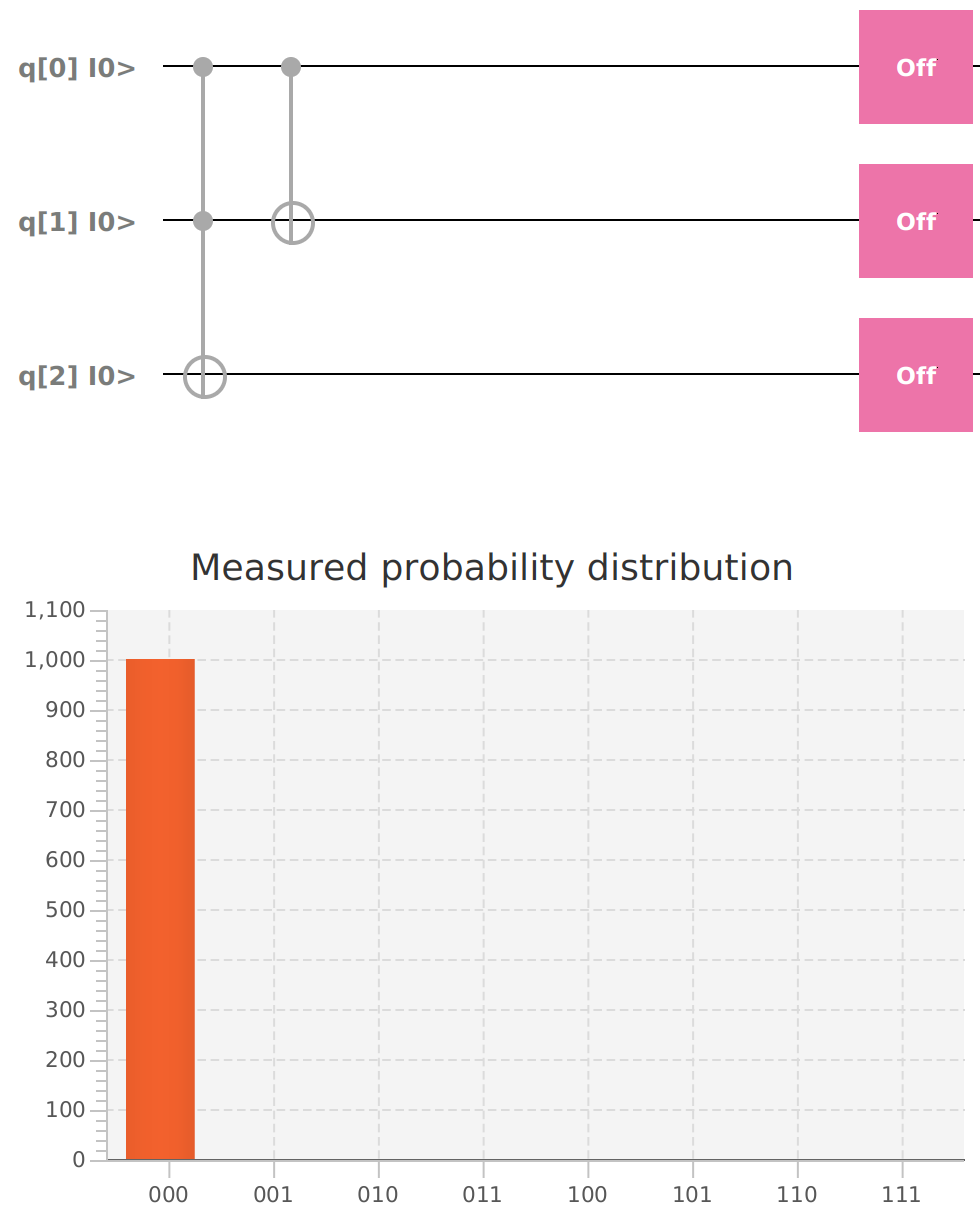
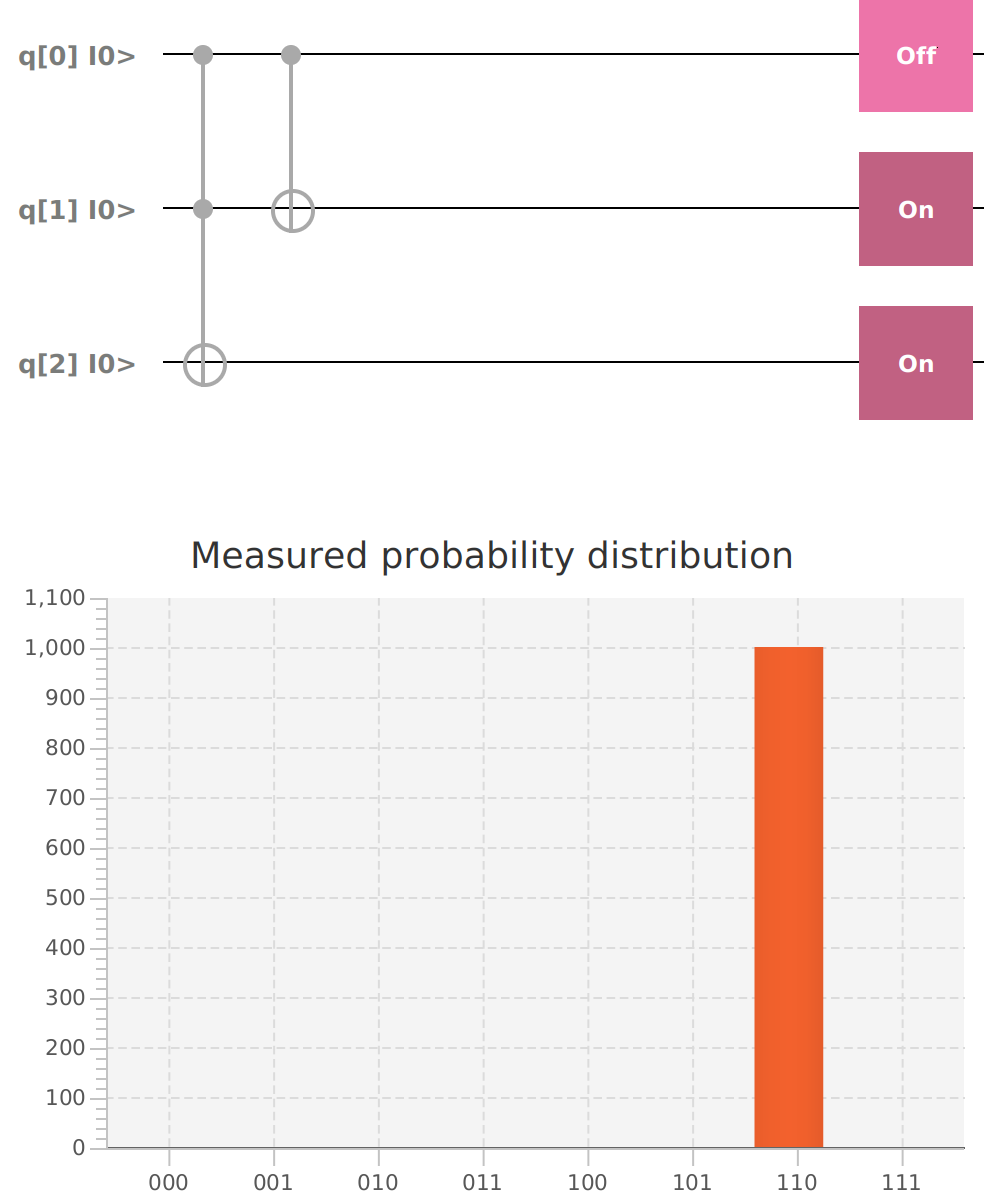
mvn clean javafx:run --quiet --file entanglement.xml

Qubit | Probability: 0.0, Mesured: 0
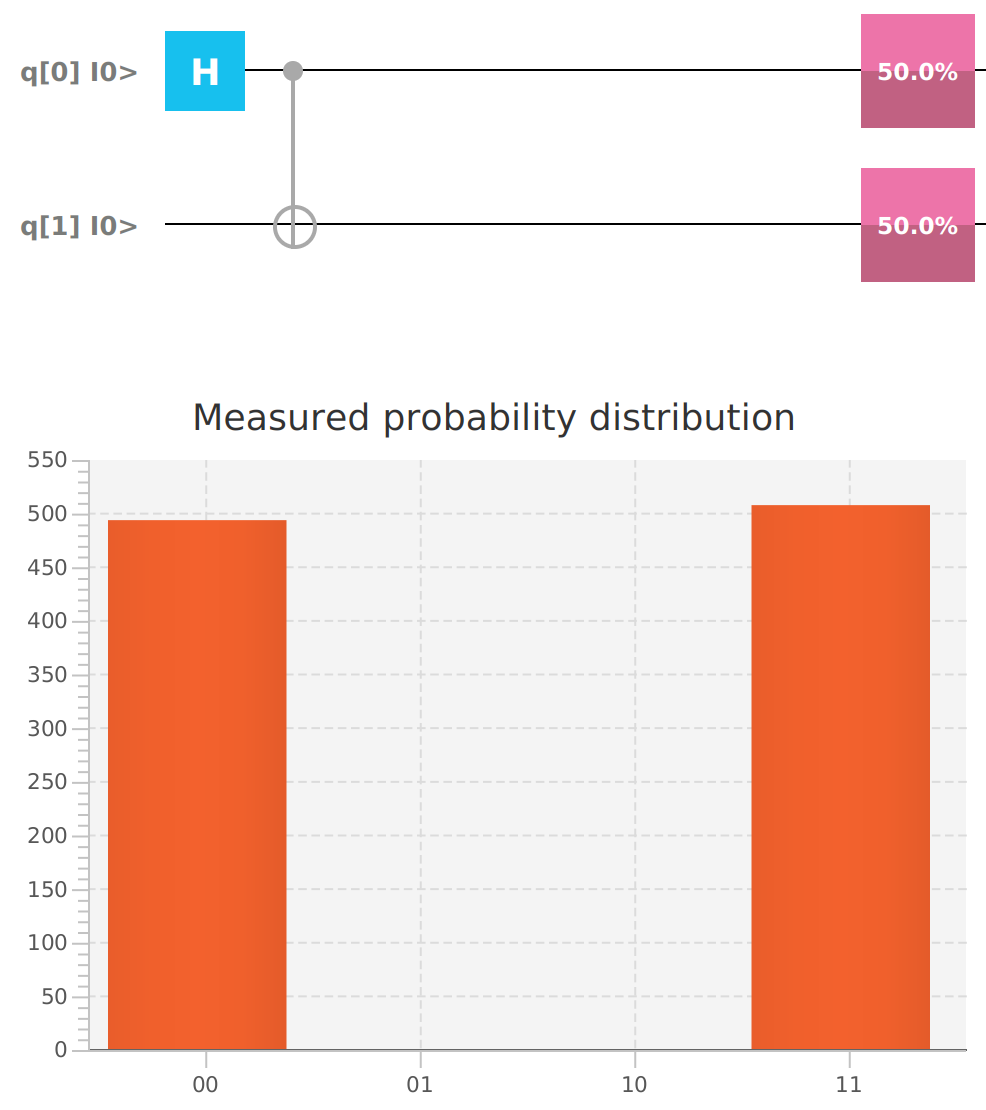
Qubit | Probability: 0.0, Mesured: 0

Bell State

Entangling 2 Qubits in superposition to create a Bell state using a Hadamard gate and a CNOT gate.

mvn clean javafx:run --quiet --file bell.xml

This results on both Qubits being either 0 or 1 50% of the time.

Qubit | Probability: 0.4999999701976776, Mesured: 0
Qubit | Probability: 0.4999999701976776, Mesured: 0

Qubit | Probability: 0.4999999701976776, Mesured: 1
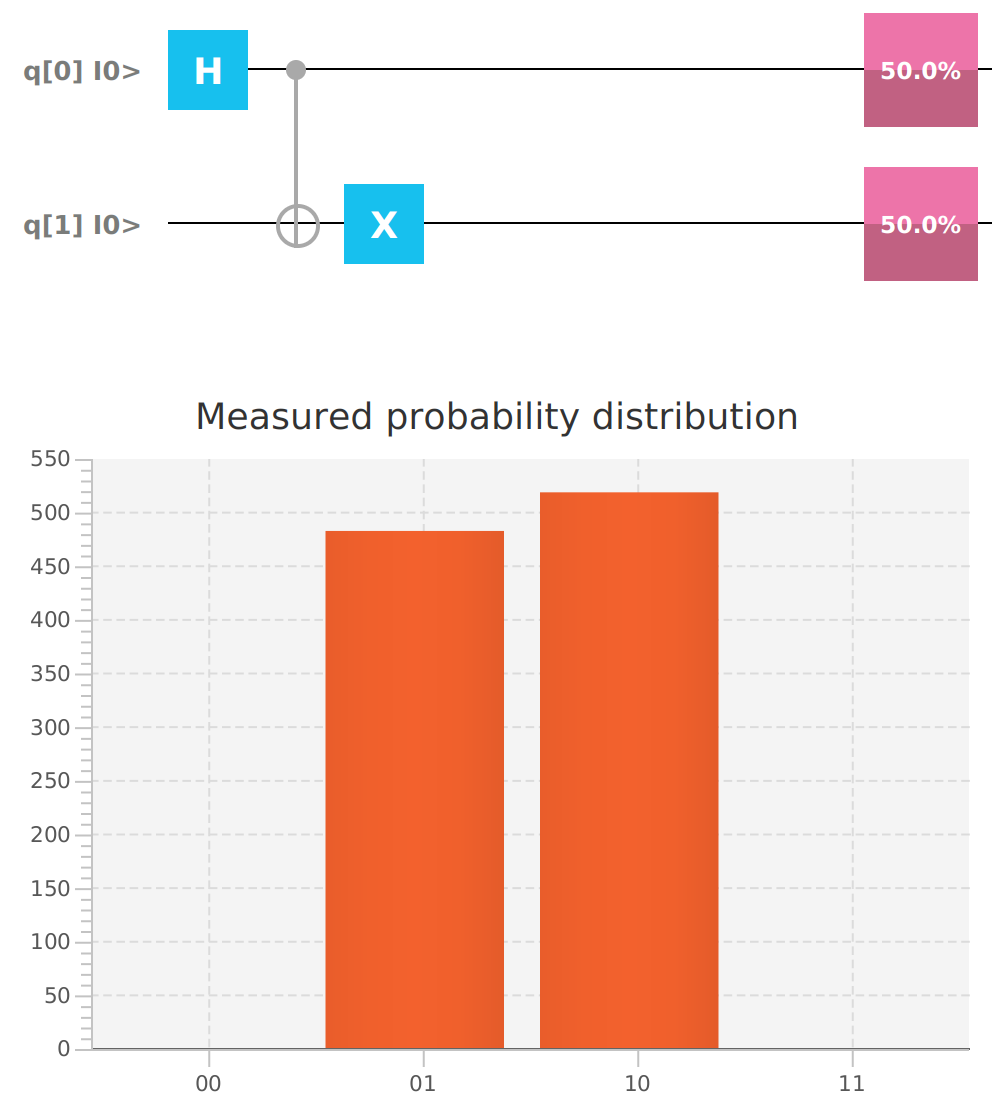
Qubit | Probability: 0.4999999701976776, Mesured: l

Adding an additional X gate to the second Qubit.

mvn clean javafx:run --quiet --file bell2.xml

It causes the Qubits to be measures as either 0 and 1 or 1 and 0 50% of the time.

Qubit | Probability: 0.4999999701976776, Mesured: 0
Qubit | Probability: 0.4999999701976776, Mesured: 1

Qubit | Probability: 0.4999999701976776, Mesured: 1
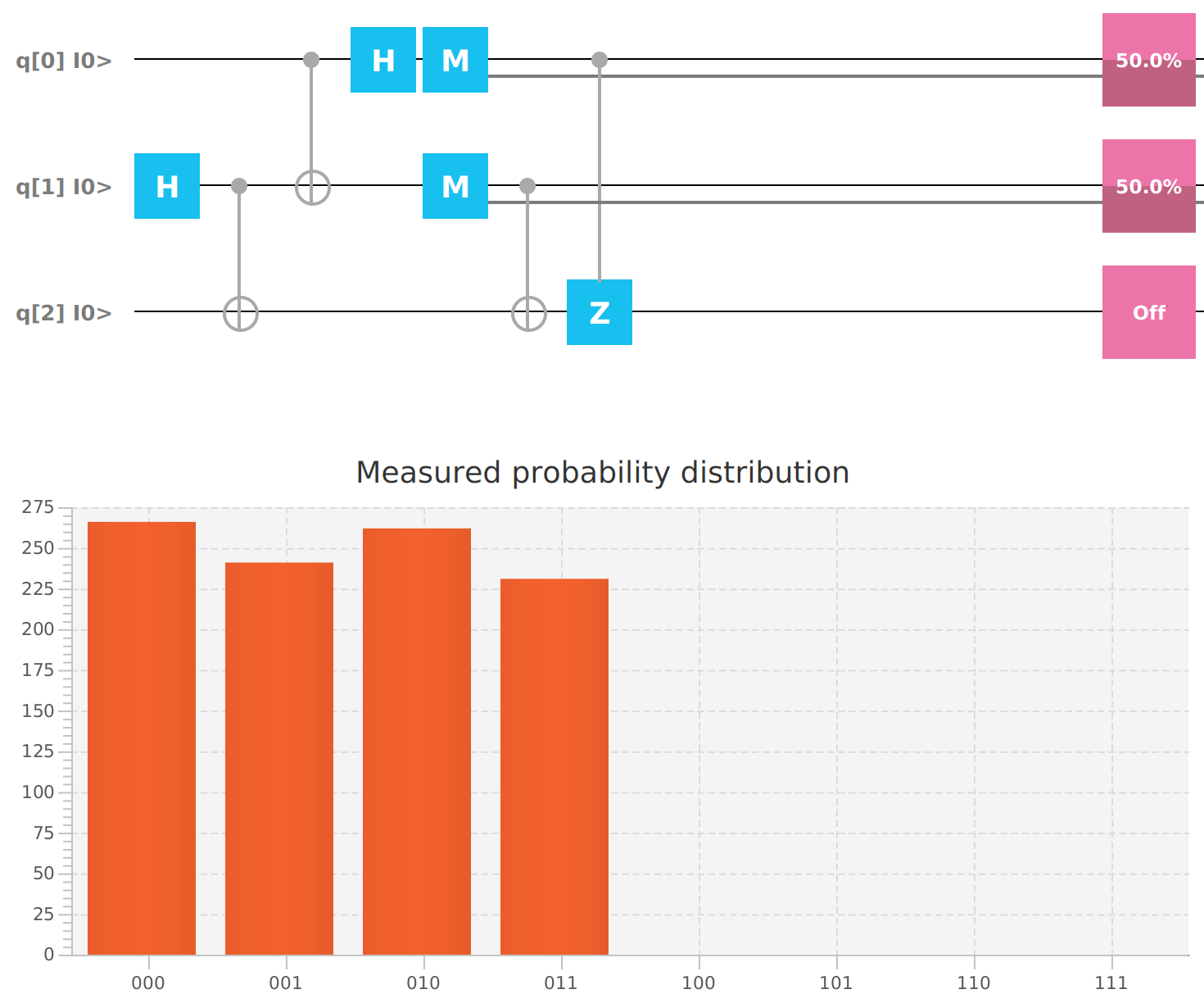
Qubit | Probability: 0.4999999701976776, Mesured: 0

Quantum Teleportation

Teleporting a Qubit from Alice to Bob by combining Hadamard and CNOT gates as well as a CZ gate.

mvn clean javafx:run --quiet --file teleport.xml

The last Qubit is guaranteed to always be 0. That means the 0 was teleported from Alice to Bob.

Qubit | Probability: 0.4999999403953552, Mesured: 0
Qubit | Probability: 0.4999999403953552, Mesured: 1
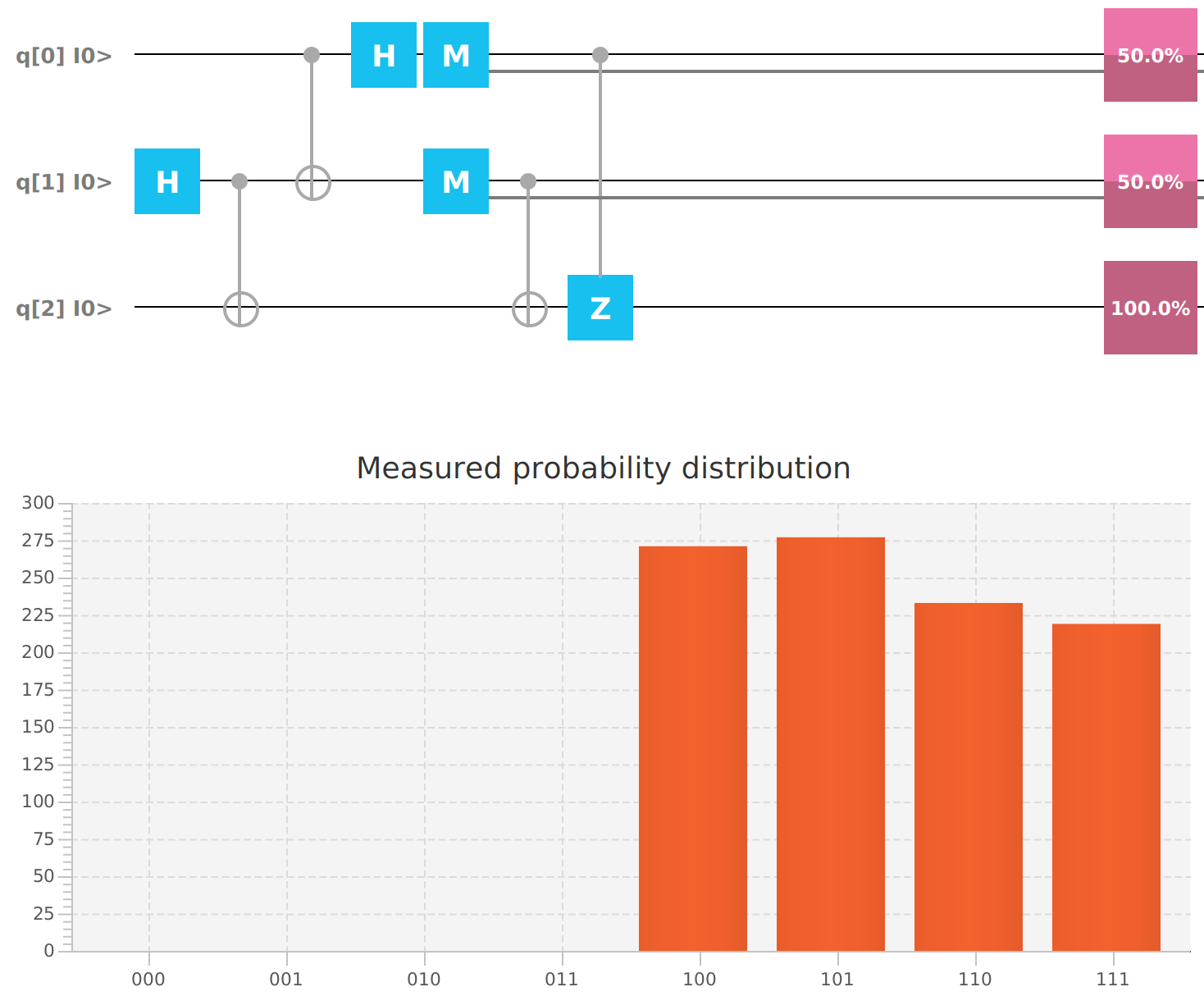
Qubit | Probability: 0.0, Mesured: 0

Now, initializing the first Qubit to 1.

mvn clean javafx:run --quiet --file teleport1.xml

Now, the value 1 has been teleported from Alice to Bob.

Qubit | Probability: 0.4999999403953552, Mesured: 1
Qubit | Probability: 0.4999999403953552, Mesured: 0
Qubit | Probability: 0.9999998807907104, Mesured: 1

Now, initializing the first Qubit to 53%.

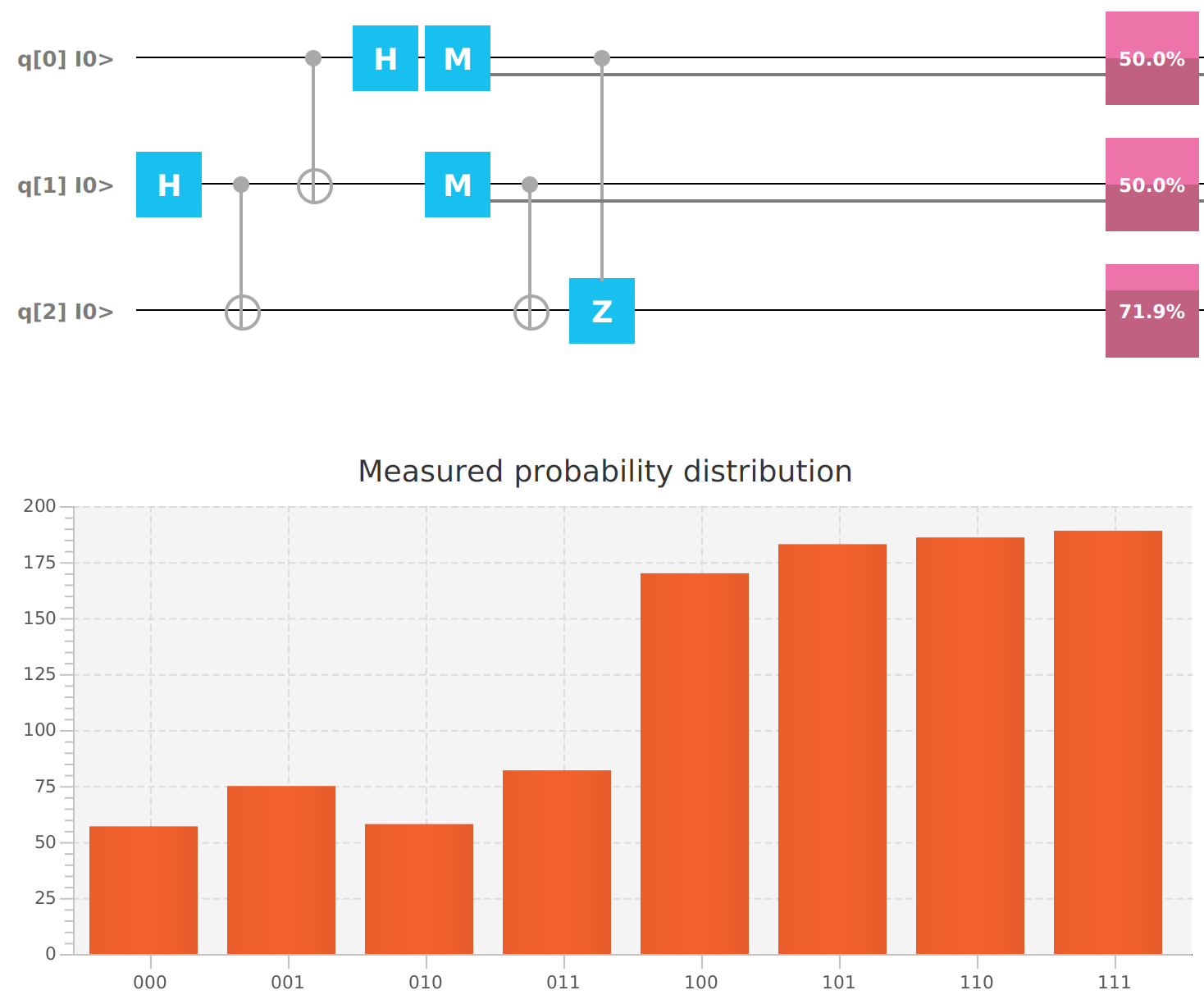
mvn clean javafx:run --quiet --file teleport53.xml

Now, the value 0.53 has been teleported from Alice to Bob after applying the formula 1 - 0.53 * 0.53 = 0.719.

Qubit | Probability: 0.4999999403953552, Mesured: 1
Qubit | Probability: 0.4999999403953552, Mesured: 0
Qubit | Probability: 0.7190999388694763, Mesured: 0

Quantum Network

Creating a network of Qubits by concatenating multiple Quantum Teleporters.

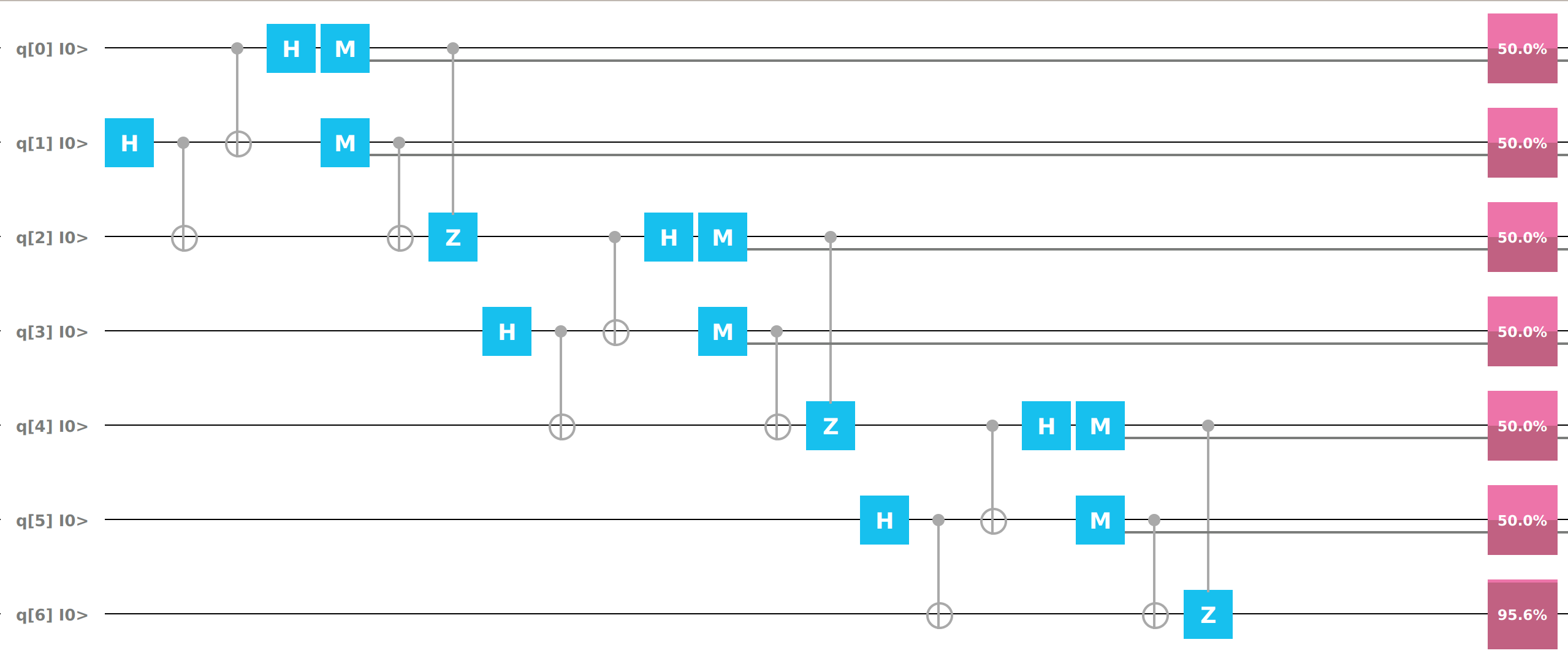
mvn clean javafx:run --quiet --file network.xml

The message 0.21 is teleported from Alice to Bob across a larger distance after applying the formula 1 - 0.21 * 0.21 = 0.9558

Qubit | Probability: 0.4999998528510332, Mesured: 1
Qubit | Probability: 0.4999998528510332, Mesured: 1
Qubit | Probability: 0.4999998528510332, Mesured: 1
Qubit | Probability: 0.4999998528510332, Mesured: 1
Qubit | Probability: 0.4999998528510332, Mesured: 1
Qubit | Probability: 0.4999998528510332, Mesured: 1
Qubit | Probability: 0.4999998528510332, Mesured: 1
Qubit | Probability: 0.4999998528510332, Mesured: 1
Qubit | Probability: 0.4999998528510332, Mesured: 0
Qubit | Probability: 0.4999998528510332, Mesured: 0
Qubit | Probability: 0.955899715423584, Mesured: 1

Quantum Inverter

Inverting the state of 2 Qubits by applying 3 consecutive CNOT gates.

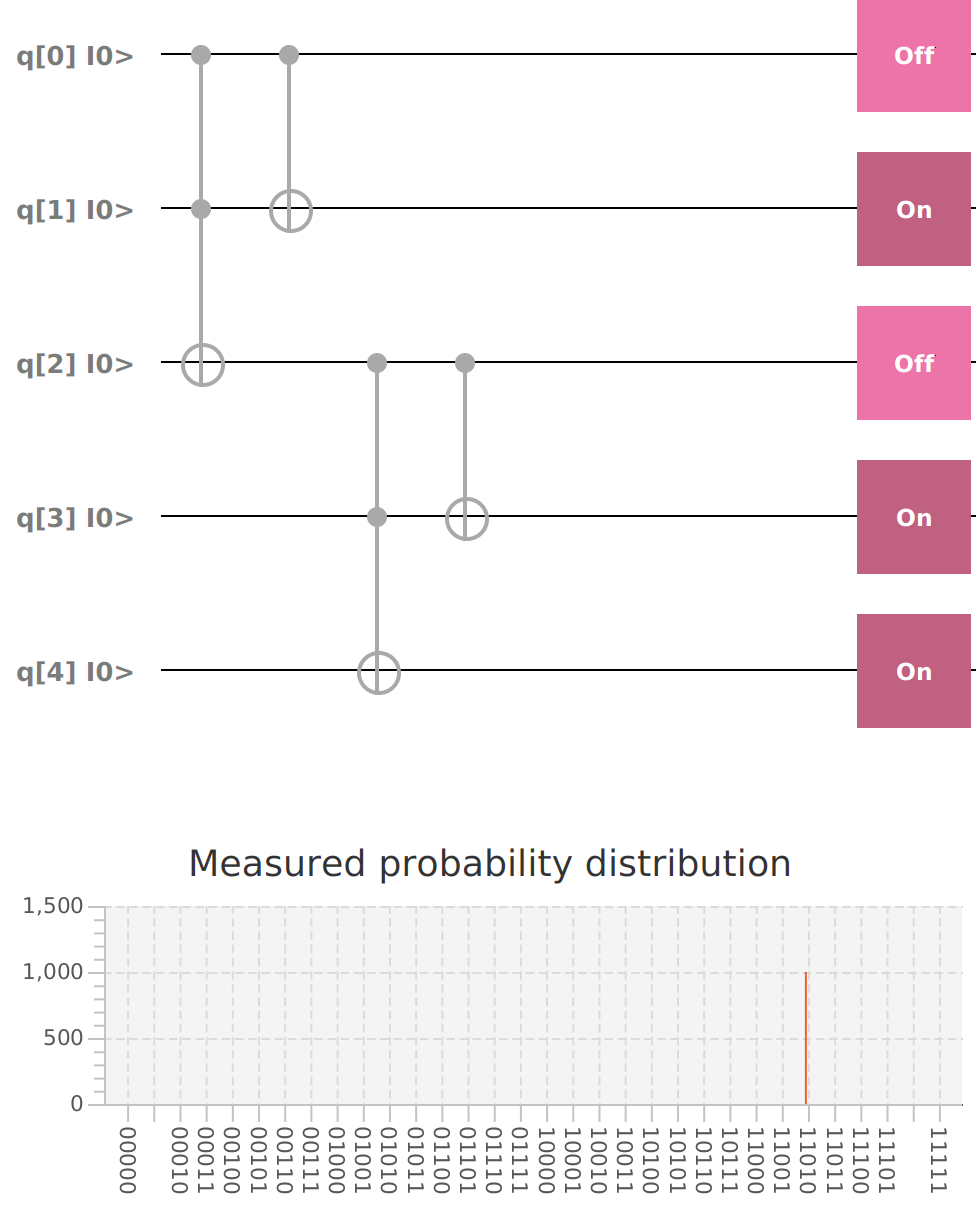
mvn clean javafx:run --quiet --file inverter.xml

The message 0.2 and 0.5 have been inverted after applying the formulas: 1 - 0.2 * 0.2 = 0.96 and 1 - 0.5 * 0.5 = 0.75.

Qubit | Probability: 0.9599999040365219, Mesured: 1
Qubit | Probability: 0.7499999087303877, Mesured: 1

The inverter can be used to teleport a Qubit while only applying the CNOT and CZ gates to contiguous gates so that they can be easily calculated mathematically.

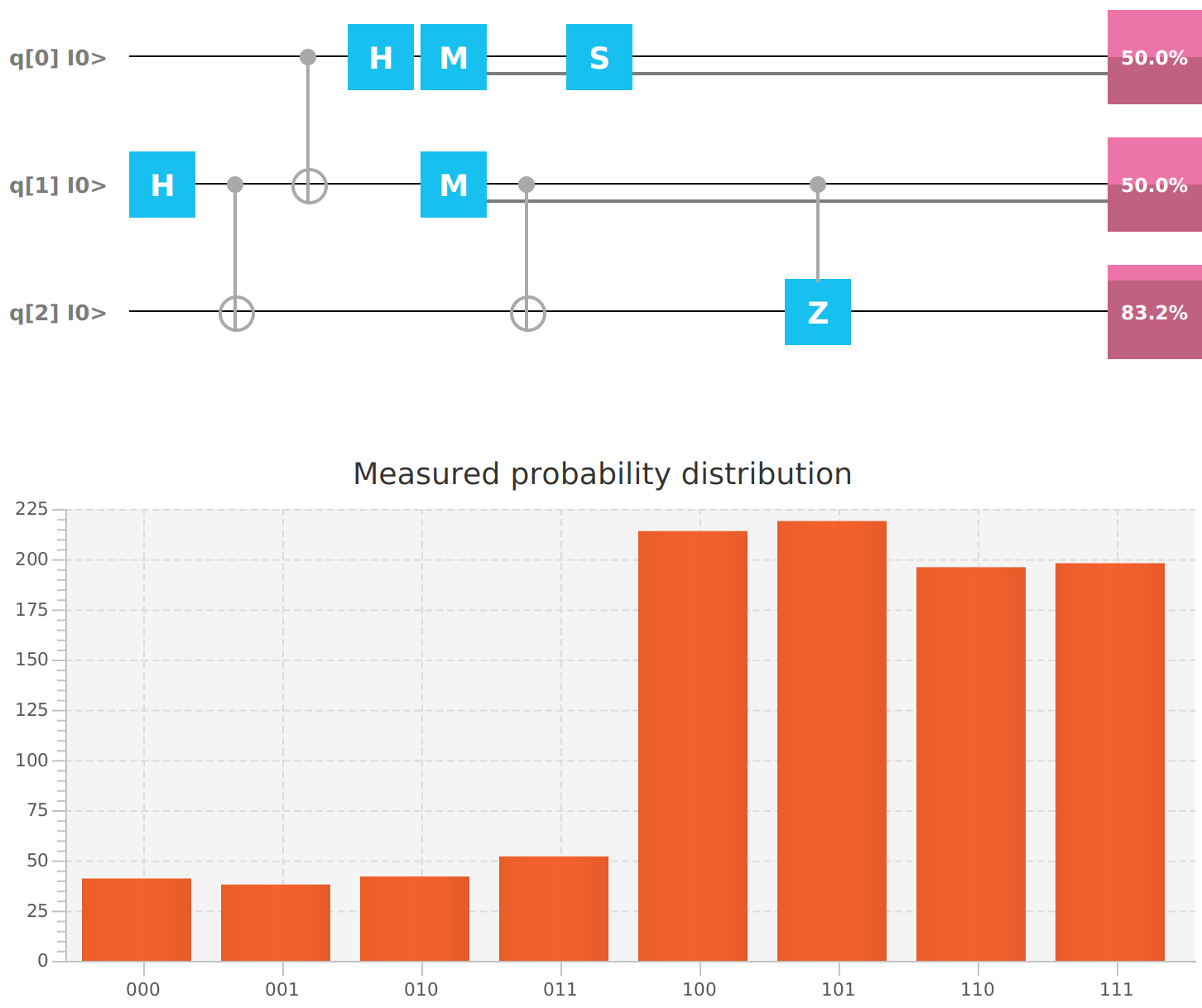
mvn clean javafx:run --quiet --file swap.xml

The message 0.41 is teleported from Alice to Bob after swapping the state of the first 2 Qubits.

Qubit | Probability: 0.5, Mesured: 0
Qubit | Probability: 0.5, Mesured: 0
Qubit | Probability: 0.8319000005722046, Mesured: 1

Quantum Adder

Summing the value of 2 Qubits using a Toffoli gate. The first Qubit is kept to guarantee the Quantum Reversibility Principle. The last Qubit is the carry bit.

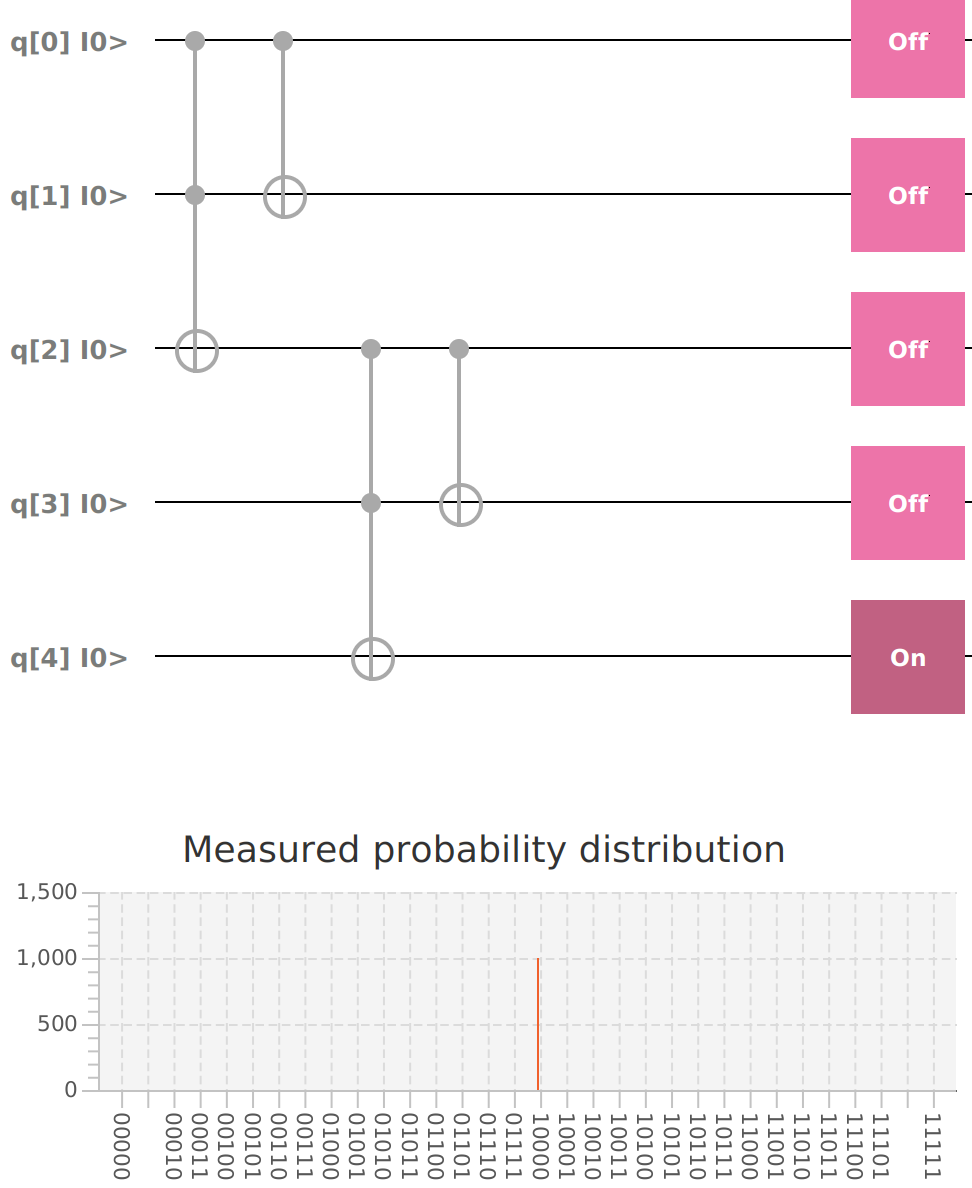
mvn clean javafx:run --quiet --file adder00.xml

Two |0> Qubits sum |00>.

Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0

Adding two |1> Qubits:

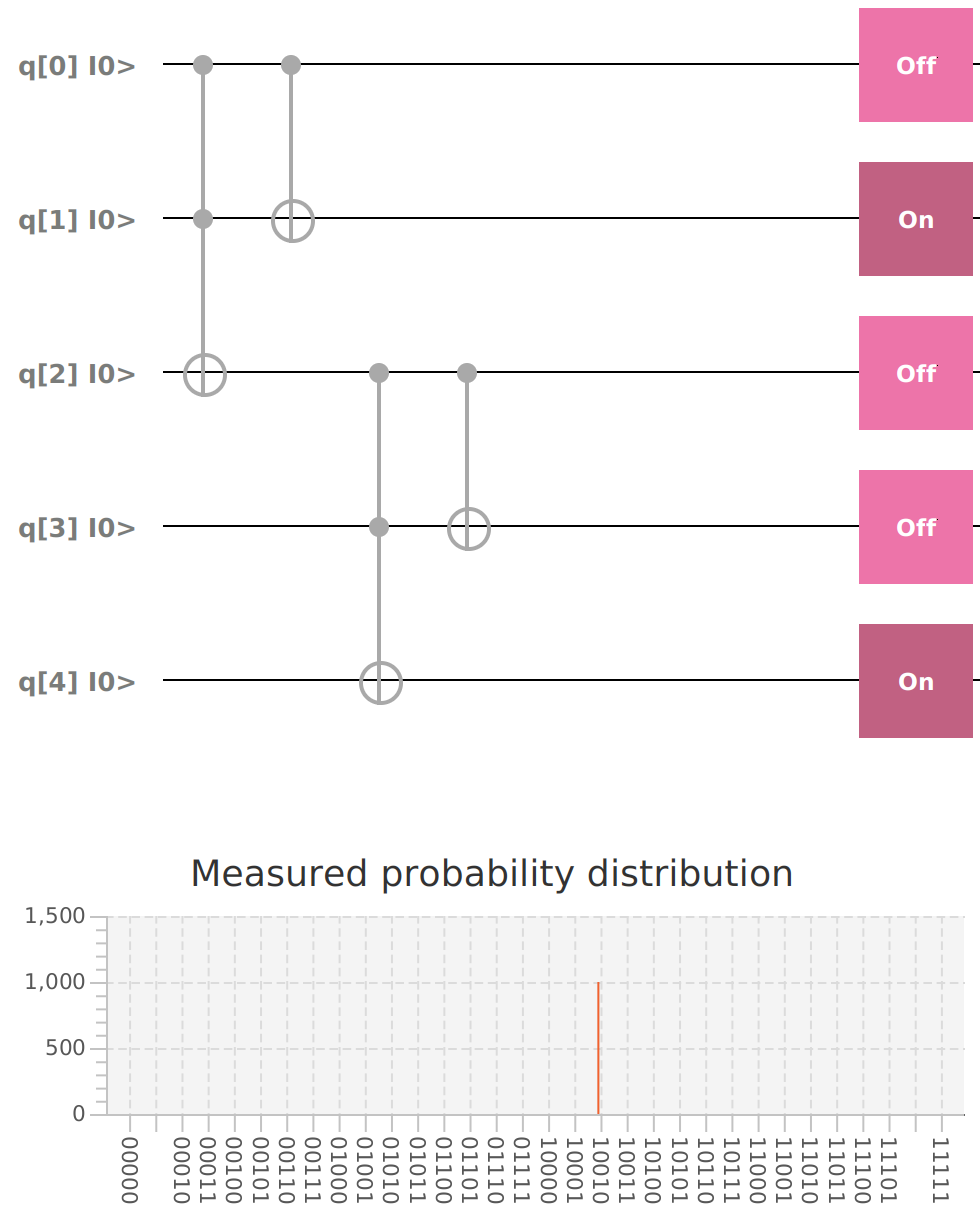
mvn clean javafx:run --quiet --file adder11.xml

Two |1> Qubits sum |10>.

Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 1.0, Mesured: 1
Qubit | Probability: 1.0, Mesured: 1

Adding |1> + |0> + |0>:

mvn clean javafx:run --quiet --file adder100.xml

The sum of |1> + |0> + |0> results in |01> (The last 2 Qubits):

Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 1.0, Mesured: 1

Adding |1> + |0> + |1>:

mvn clean javafx:run --quiet --file adder101.xml

The sum of |1> + |0> + |1> results in |10> (the last 2 Qubits):

Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 1.0, Mesured: 1
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 1.0, Mesured: 1

Adding |1> + |1> + |1>:

mvn clean javafx:run --quiet --file adder111.xml

The sum of |1> + |1> + |1> results in |11> (The last 2 Qubits):

Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 1.0, Mesured: 1
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 1.0, Mesured: 1
Qubit | Probability: 1.0, Mesured: 1

BB84 Algorithm

Sending a message over the network, taking advantage of the Hadamard gate resulting in the original Qubit if applied twice.

mvn clean javafx:run --quiet --file bb84.xml

The |1001> Qubits sent by Alice are received as |1001> by Bob.

Qubit | Probability: 0.9999997615814209, Mesured: 1
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.9999997615814209, Mesured: 1

Eve is listening on the network and randomly applies Hadamard gates to try to get the message. After that, retransmits the Qubit to Bob who applies the same Hadamard configuration that Alice randomly applied.

mvn clean javafx:run --quiet --file eavesdropping.xml

The |1001> Qubits sent by Alice are not properly received by Eve, who can not forward a message to Bob without him noticing that the message has been tampered.

Qubit | Probability: 0.9999997615814209, Mesured: 1
Qubit | Probability: 0.49999988079071045, Mesured: 1
Qubit | Probability: 0.0, Mesured: 0
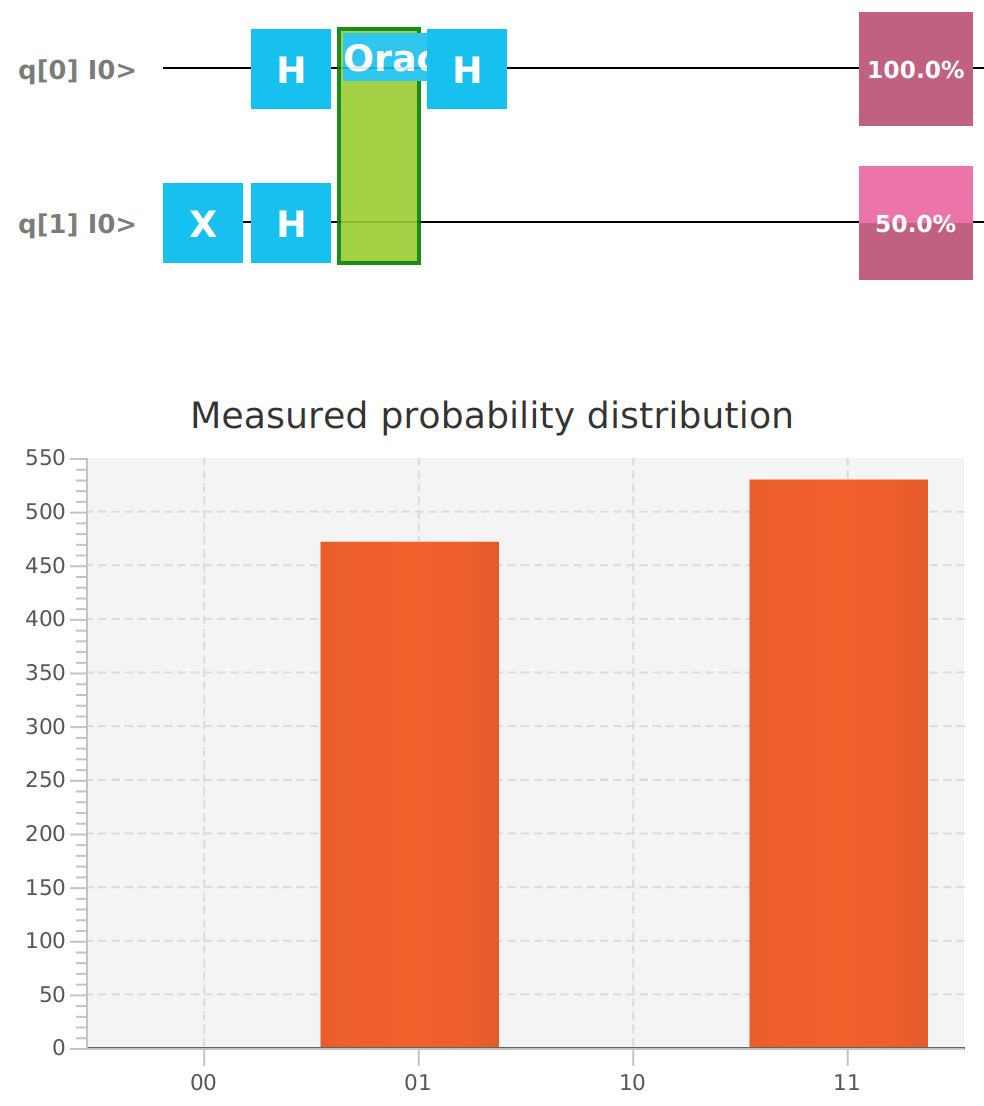
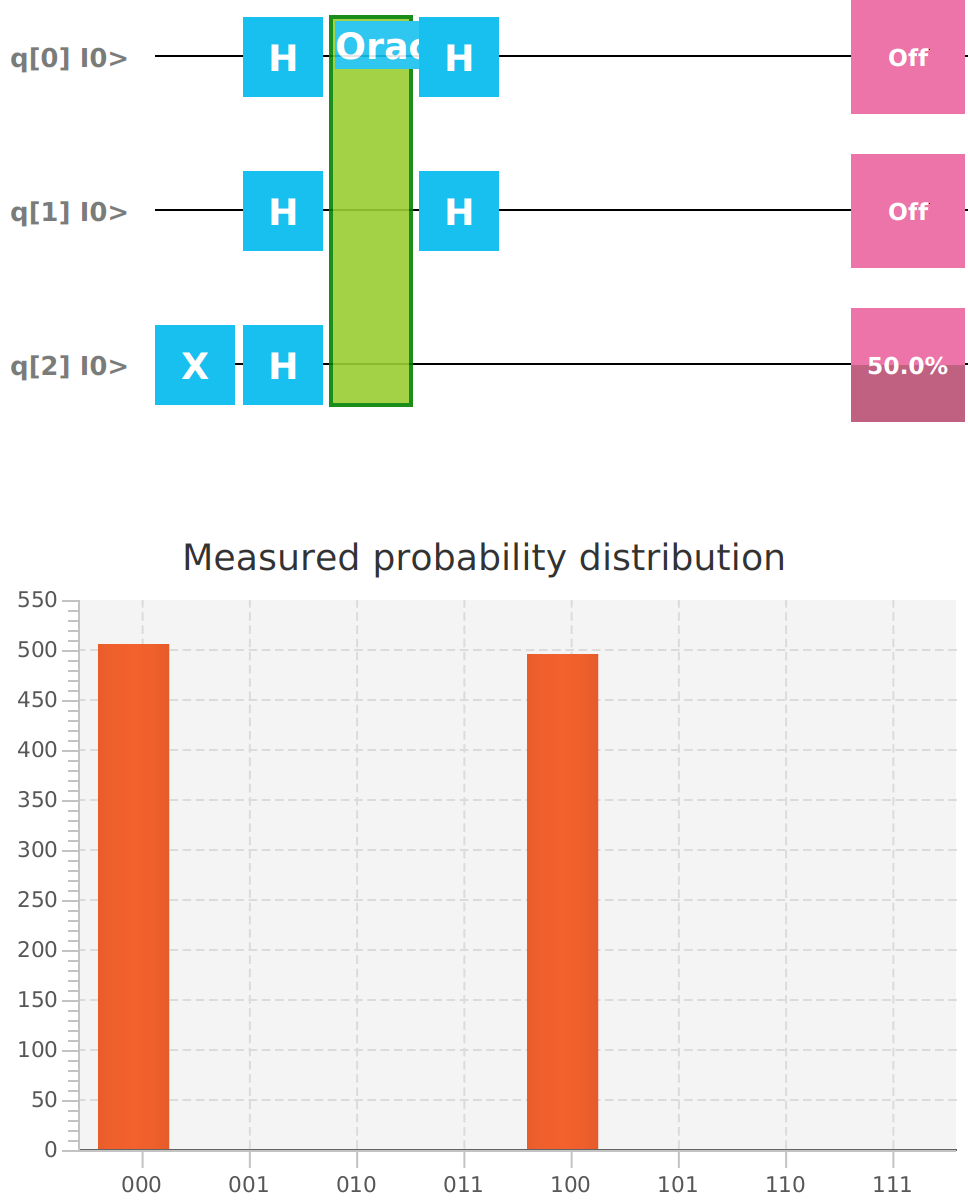
Qubit | Probability: 0.49999988079071045, Mesured: 1

Deutsch Josza Algorithm

Running the Deutsch Algorithm with a random Oracle that is unknown at run time:

mvn clean javafx:run --quiet --file deutschjozsa.xml

If the Oracle is a constant function, the measured value of the first Qubit is guaranteed to be 0. If the Oracle is a balanced function, the measured value of the first Qubit is guaranteed to be 1.

Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 1
----------------------------------------------------
Qubit | Function: 1 Type: balanced
Qubit | Probability: 0.9999998211860657, Mesured: 1
Qubit | Probability: 0.49999991059303284, Mesured: 0
----------------------------------------------------
Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 1
----------------------------------------------------
Qubit | Function: 1 Type: balanced
Qubit | Probability: 0.9999998211860657, Mesured: 1
Qubit | Probability: 0.49999991059303284, Mesured: 0
----------------------------------------------------
Qubit | Function: 1 Type: balanced
Qubit | Probability: 0.9999998211860657, Mesured: 1
Qubit | Probability: 0.49999991059303284, Mesured: 1
----------------------------------------------------
Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 0
----------------------------------------------------
Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 1
----------------------------------------------------
Qubit | Function: 1 Type: balanced
Qubit | Probability: 0.9999998211860657, Mesured: 1
Qubit | Probability: 0.49999991059303284, Mesured: 0
----------------------------------------------------
Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 1
----------------------------------------------------
Qubit | Function: 1 Type: balanced
Qubit | Probability: 0.9999998211860657, Mesured: 1
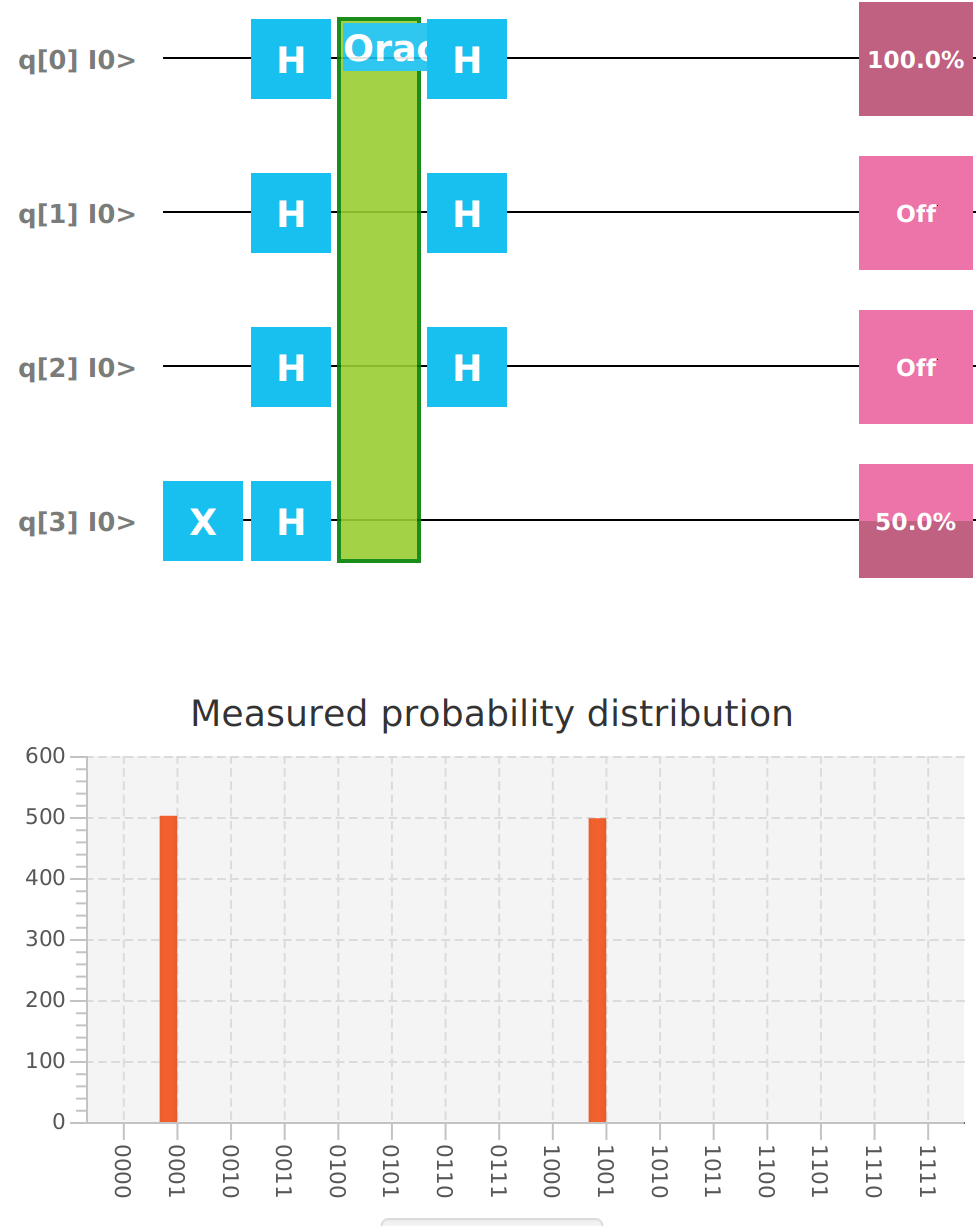
Qubit | Probability: 0.49999991059303284, Mesured: 0

Running the Deutsch Algorithm with 2 Qubits.

mvn clean javafx:run --quiet --file deutschjozsa2.xml

If the Oracle is a constant function, the measured value of the first Qubit is guaranteed to be 0. If the Oracle is a balanced function, the measured value of the first Qubit is guaranteed to be 1.

Qubit | Function: 1 Type: balanced
Qubit | Probability: 0.9999998211860657, Mesured: 1
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 0
----------------------------------------------------
Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 0
----------------------------------------------------
Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 0

Running the Deutsch Algorithm with 3 Qubits.

mvn clean javafx:run --quiet --file deutschjozsa3.xml

If the Oracle is a constant function, the measured value of the first Qubit is guaranteed to be 0. If the Oracle is a balanced function, the measured value of the first Qubit is guaranteed to be 1.

Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 0
----------------------------------------------------
Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 1
----------------------------------------------------
Qubit | Function: 1 Type: balanced
Qubit | Probability: 0.9999998211860657, Mesured: 1
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 0

Running the Deutsch-Jozsa Algorithm with N Qubits.

mvn clean javafx:run --quiet --file deutschjozsa10.xml

If the Oracle is a constant function, the measured value of the first Qubit is guaranteed to be 0. If the Oracle is a balanced function, the measured value of the first Qubit is guaranteed to be 1.

Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 0
----------------------------------------------------
Qubit | Function: 0 Type: constant
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 0
----------------------------------------------------
Qubit | Function: 1 Type: balanced
Qubit | Probability: 0.9999998211860657, Mesured: 1
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.0, Mesured: 0
Qubit | Probability: 0.49999991059303284, Mesured: 0

Grover's Search Algorithm

Running the Deutsch Algorithm with a random Oracle that is unknown at run time:

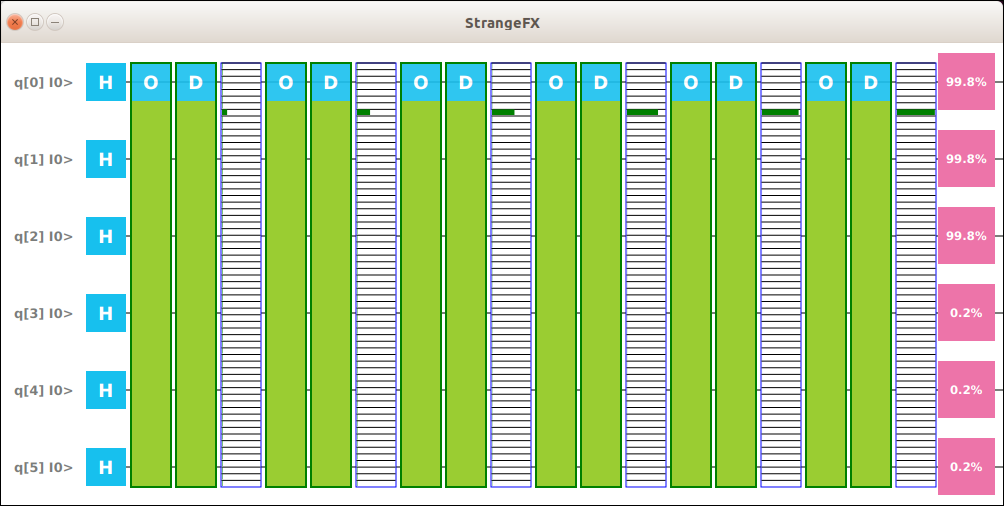
mvn clean javafx:run --quiet --file grover.xml

The algorithm iterates multiple times applying the Oracle and the Diffusor. In each iteration, the probability of measuring the expected solution increases.

In this case, there are 3 Qubits which can encode 8 values. In other words, 3 Qubits can be used to search for a match among 8 records.

Qubits | Qubits: 3 Encoded: 8 Solution: 2 Runs: 2.221441469079183
----------------------------------------------------
Correct Solution Probability after step 1: 0.7812497615814209
Correct Solution Probability after step 2: 0.9453120827674866
----------------------------------------------------
Probability distribution at step: 1
p: 0.031249988824129105
p: 0.031249988824129105
p: 0.7812497615814209
p: 0.031249988824129105
p: 0.031249988824129105
p: 0.031249994412064552
p: 0.031249988824129105
p: 0.031249983236193657
----------------------------------------------------
Probability distribution at step: 2
p: 0.007812506519258022
p: 0.007812506519258022
p: 0.9453120827674866
p: 0.007812506519258022
p: 0.007812500931322575
p: 0.007812506519258022
p: 0.007812500931322575
p: 0.007812498603016138

Running the Deutsch Algorithm with a random Oracle that is unknown at run time:

mvn clean javafx:run --quiet --file grovern.xml

This time, the Grover's Search algorithm is able to search for a match among 256 records. As a conclusion, the computation increases exponentially with the amount of entangled Qubits.

Qubits | Qubits: 8 Encoded: 256.0 Solution: 2 Runs: 12.566370614359172
----------------------------------------------------
Correct Solution Probability after step 1: 0.03479098901152611
Correct Solution Probability after step 2: 0.09463772177696228
Correct Solution Probability after step 3: 0.17972062528133392
Correct Solution Probability after step 4: 0.2847433090209961
Correct Solution Probability after step 5: 0.40317079424858093
Correct Solution Probability after step 6: 0.527620255947113
Correct Solution Probability after step 7: 0.6503432393074036
[...]