Aka Whittaker-Henderson, Whittaker-Eilers Smoother is known as the perfect smoother. Its a discrete-time version of spline smoothing for equally spaced data. It minimizes the functional
where y are the datapoints, z is the smoothed function, and
The smoothed output can be obtained by solving the linear system
difference_matrix for its construction).
Here we see the wood dataset smoothed whith both order 2 and 3.
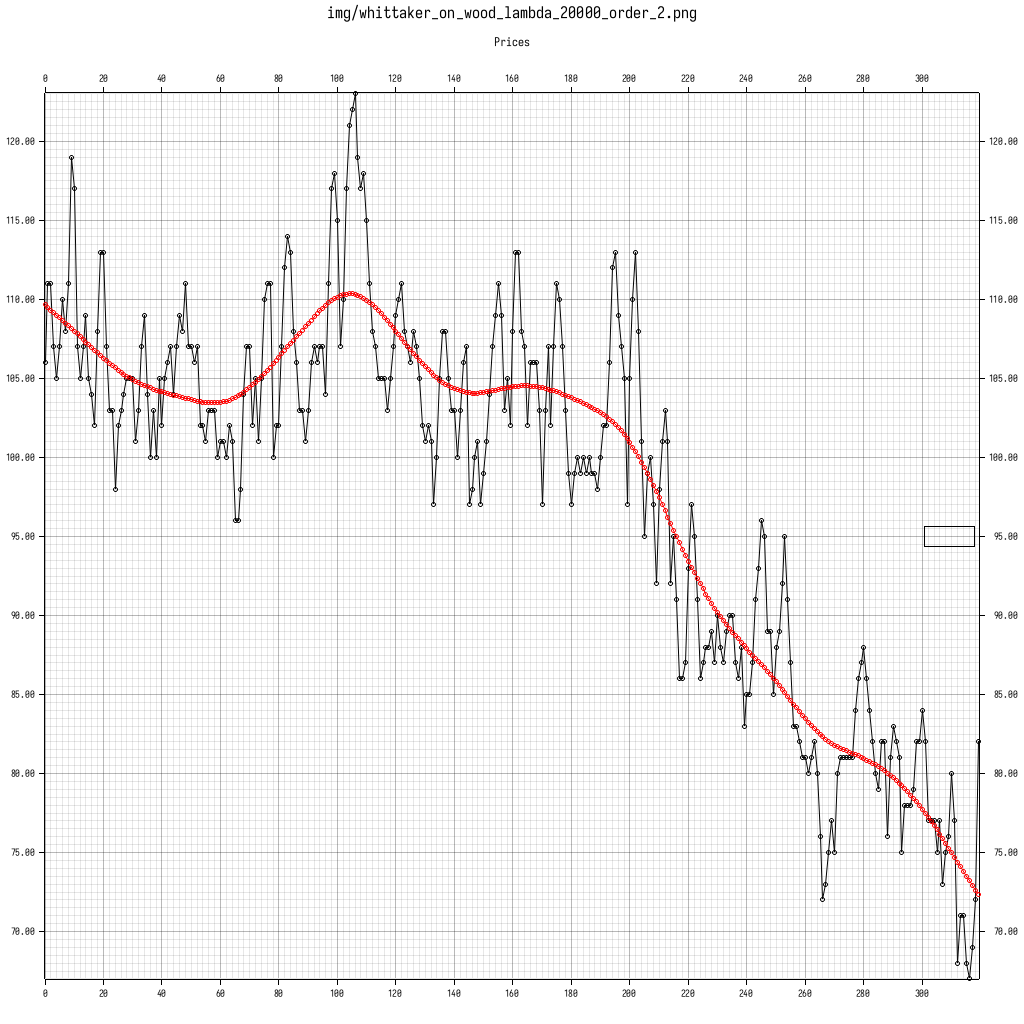
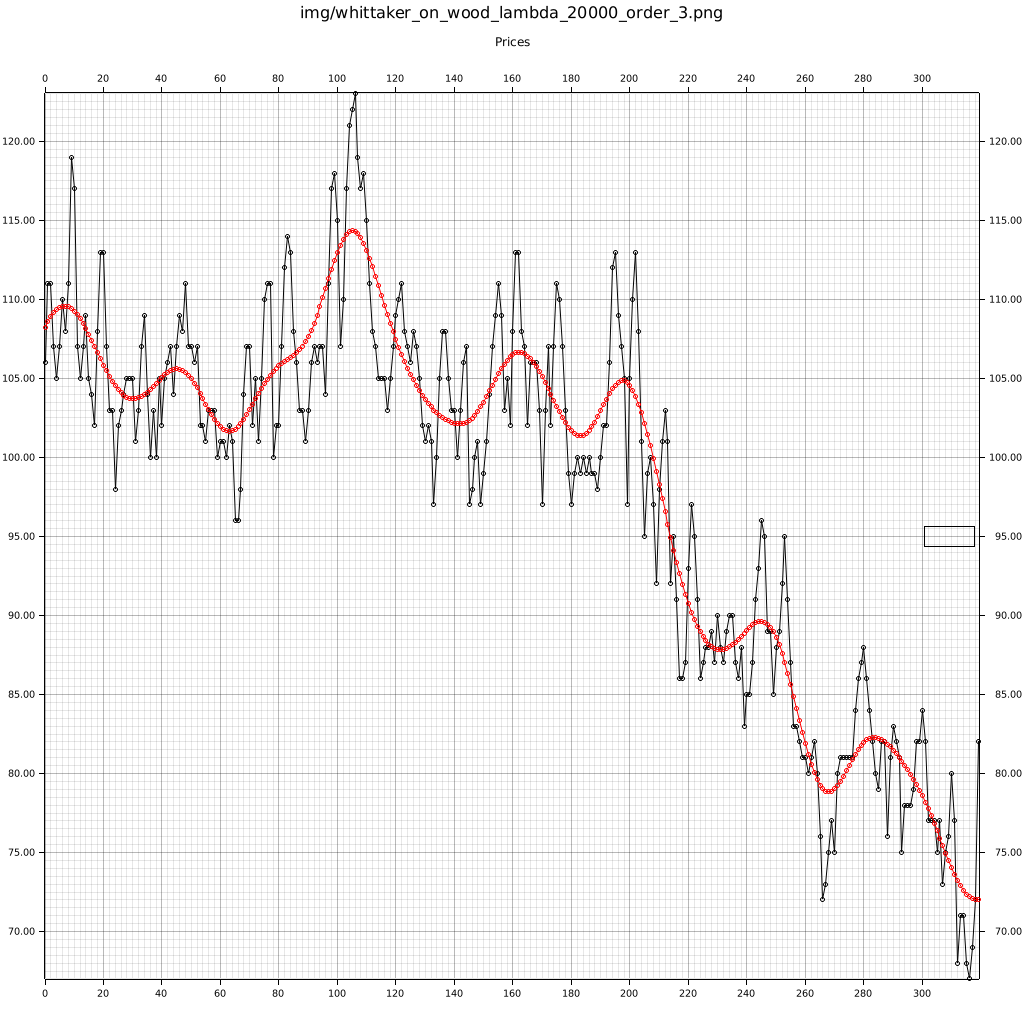
Compared to a moving average smoother, this method does not suffer from a group-delay.
Compared to a convolution kernel such as the savitzky-golay filter, the values at the edge are well defined and don't need to be interpolated. The savitzky-golay filter does have a nice flat passband, but suffers from unsatisfactory high-frequency noise, which is not sufficiently suppressed. This is a particular problem when the derivative of the data is of importance.
However, this smoother takes future values into account and therefore suffers from a look-ahead bias.
To use this smoother in you project, add this to your Cargo.toml:
[dependencies]
whittaker_smoother = "0.1"Now you can use the smoothing function as such:
use whittaker_smoother::whittaker_smoother;
// Here we use the WOOD_DATASET, but this can be any series that you would like to smooth
let raw = Vec::from_iter(WOOD_DATASET.iter().map(|v| *v as f64));
let lambda = 2e4;
let order = 3;
let smoothed = whittaker_smoother(&raw, lambda, order).unwrap();And BAM, that's it! There is you perfectly smoothed series.
See the papers folder for two papers showing additional details of the method.
This implementation was inspired by A python implementation.
- Add benchmarks
- Use sparse matrices if available
- Add function for computing the optimal lambda based on cross-validation (See eilers2003)
Copyright (C) 2020 <Mathis Wellmann wellmannmathis@gmail.com>
This program is free software: you can redistribute it and/or modify it under the terms of the GNU Affero General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU Affero General Public License for more details.
You should have received a copy of the GNU Affero General Public License along with this program. If not, see https://www.gnu.org/licenses/.
