Max O’Cull 3/23/2020
Data sources can be found at John Hopkin’s Github.
confirmed_raw <- read.csv("./time_series_19-covid-Confirmed.csv", header = TRUE)
recovered_raw <- read.csv("./time_series_19-covid-Recovered.csv", header = TRUE)
deaths_raw <- read.csv("./time_series_19-covid-Deaths.csv", header = TRUE)
indy_confirmed <- as.data.frame(t((confirmed_raw[confirmed_raw$Province.State == "Indiana", ])[,5:ncol(confirmed_raw)]))
indy_recovered <- as.data.frame(t((recovered_raw[recovered_raw$Province.State == "Indiana", ])[,5:ncol(recovered_raw)]))
indy_dead <- as.data.frame(t((deaths_raw[deaths_raw$Province.State == "Indiana", ])[,5:ncol(deaths_raw)]))
indy_all <- data.frame(seq(22, nrow(indy_confirmed) + 22 - 1), indy_confirmed, indy_recovered, indy_dead)
colnames(indy_all) <- c("Day", "Confirmed", "Recovered", "Dead")
sk_confirmed <- as.data.frame(t((confirmed_raw[confirmed_raw$Country.Region == "Korea, South", ])[,5:ncol(confirmed_raw)]))
sk_recovered <- as.data.frame(t((recovered_raw[recovered_raw$Country.Region == "Korea, South", ])[,5:ncol(recovered_raw)]))
sk_dead <- as.data.frame(t((deaths_raw[deaths_raw$Country.Region == "Korea, South", ])[,5:ncol(deaths_raw)]))
sk_all <- data.frame(seq(22, nrow(sk_confirmed) + 22 - 1), sk_confirmed, sk_recovered, sk_dead)
colnames(sk_all) <- c("Day", "Confirmed", "Recovered", "Dead")
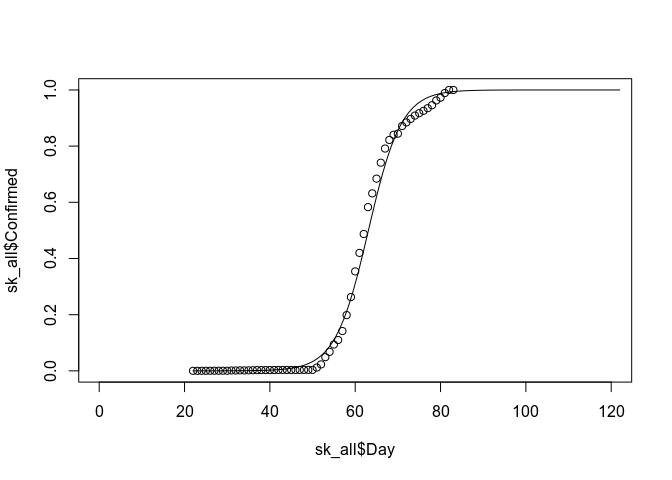
sk_all$Confirmed <- sk_all$Confirmed / max(sk_all$Confirmed) # This is literally just a guess...
sk_fit <- glm(Confirmed ~ Day, data = sk_all, family = binomial)## Warning in eval(family$initialize): non-integer #successes in a binomial
## glm!
summary(sk_fit)##
## Call:
## glm(formula = Confirmed ~ Day, family = binomial, data = sk_all)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.209710 -0.083779 0.007963 0.038130 0.178700
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -16.29510 4.73700 -3.440 0.000582 ***
## Day 0.25825 0.07479 3.453 0.000554 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 54.02933 on 61 degrees of freedom
## Residual deviance: 0.63146 on 60 degrees of freedom
## AIC: 16.77
##
## Number of Fisher Scoring iterations: 7
plot(sk_all$Day, sk_all$Confirmed, ylim=c(0, 1), xlim=c(0, 120))
sk_pred_range <- seq(22, 122, length.out = 100)
sk_pred <- predict(sk_fit, newdata = data.frame(Day = sk_pred_range), type = "response")
lines(sk_pred_range, sk_pred)# Indy
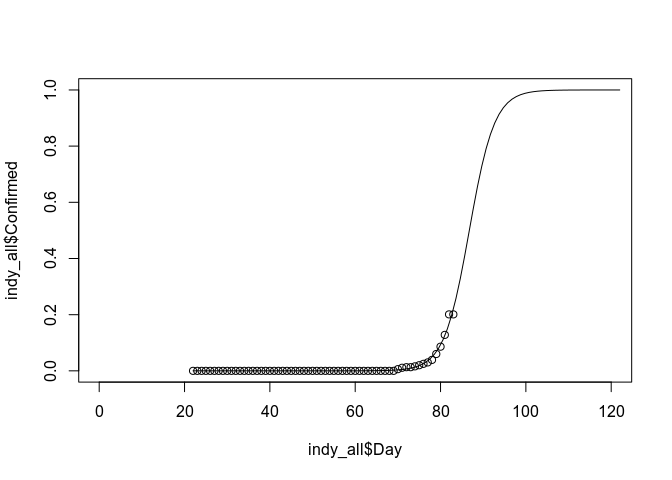
indy_all$Confirmed <- indy_all$Confirmed / 1000 # This is literally just a guess...
# If we optimize on the total confirmed cases (the 1000 magic value) such that
# R^2 is maximized ~~we'll overfit~~ we'll find the most likely scenario.
indy_fit <- glm(Confirmed ~ Day, data = indy_all, family = binomial)## Warning in eval(family$initialize): non-integer #successes in a binomial
## glm!
summary(indy_fit)##
## Call:
## glm(formula = Confirmed ~ Day, family = binomial, data = indy_all)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.070369 -0.012482 -0.001123 -0.000085 0.088017
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -29.3280 29.5306 -0.993 0.321
## Day 0.3381 0.3685 0.918 0.359
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 3.494683 on 61 degrees of freedom
## Residual deviance: 0.045895 on 60 degrees of freedom
## AIC: 5.8228
##
## Number of Fisher Scoring iterations: 11
plot(indy_all$Day, indy_all$Confirmed, ylim=c(0, 1), xlim=c(0, 120))
indy_pred_range <- seq(22, 122, length.out = 100)
indy_pred <- predict(indy_fit, newdata = data.frame(Day = indy_pred_range), type = "response")
lines(indy_pred_range, indy_pred)