基础算法

排序

快速排序

快速排序算法模板 —— 模板题

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

思路：

确定分界点： q[l] ， q[r] , q[(l+r)/2] ，随机 。随便挑一个值为x
调整区间，左边区间所有的数 ≤x , 右边区间所有的数 ≥x（🌟）
递归处理左右两段

解法：

双指针左右 i，j双指针，将左指针i向右边移动，当指针所指数不满足小于等于x的时候，左指针停下，右指针向左移动，当右指针所指数不满足大于等于x的时候，右指针停下，左右指针所指的数相互交换，交换后满足左右指针的条件，可以继续移动，当i>j时，就是已经遍历完整个数组，则递归。

    package main
    
    import "fmt"
    
    func main() {
    	var arr = []int{3, 12, 5, 2, 12, 1, 63, 76}
    	for _, v := range arr {
    		fmt.Print(v, "\t")
    	}
    
    	quickSort(arr, 0, len(arr)-1)
    	fmt.Println()
    	for _, v := range arr {
    		fmt.Print(v, "\t")
    	}
    }
    
    func quickSort(arr []int, l, r int) {
        if l >= r {
    		return
    	} //确定边界
    	// 减1，加1是为了从让指针先移动再做比较
    	i := l - 1  //左指针
    	j := r + 1  //右指针
    	x := arr[(l+r)>>1] //随便去一个值
    	for i < j {
    		for {
    			i++ //左指针向右移动后在做比较
    			if arr[i] >= x {
    				break //左指针指向的值不满足<=x
    			}
    		}
    		for {
    			j-- //右指针向左移动后在做比较
    			if arr[j] <= x {
    				break //右指针指向的值不满足>=x
    			}
    		}
    		if i < j {
    			arr[i], arr[j] = arr[j], arr[i]
    		}
    	}
    	quickSort(arr, l, j)
    	quickSort(arr, j+1, r)
    }

归并排序

归并排序算法模板 —— 模板题

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

思路：

确定分界点：mid = （l+r）/2
递归排序left，right
归并 ——合二为一（🌟）

解法：

双指针

首先确定分界点
选中间值
递归
取 i，j 两指针为左右两个区间的开始
i，j 两指针所指值比较，较小的值添加到临时数组，并向前移动，直到结尾
将两区间剩余到值添加到临时数组中
将临时数组中到值，拿回到原来数组中

package main

import "fmt"

func main() {
	var arr = []int{3, 12, 5, 2, 12, 1, 63, 76}
	for _, v := range arr {
		fmt.Print(v, "\t")
	}

	fmt.Println()
	mergeSort(arr, 0, len(arr)-1)
	fmt.Println()
	for _, v := range arr {
		fmt.Print(v, "\t")
	}
}

func mergeSort(q []int, l, r int) {
	// 	1. 首先确定分界点
	if l >= r {
		return
	}
	// 2. 选中间值
	mid := (l + r) >> 1
	// 3. 递归
	mergeSort(q, l, mid)
	mergeSort(q, mid+1, r)
	// 4. 取 i，j 两指针为左右两个区间的开始
	k := 0
	i := l
	j := mid + 1
	tmp := make([]int, len(q))
	// 5. i,j向前移动，i，j 两指针所指值比较，较小的值添加到临时数组，直到结尾
	for i <= mid && j <= r {
		if q[i] <= q[j] {
			tmp[k] = q[i]
			i++
			k++
		} else {
			tmp[k] = q[j]
			j++
			k++
		}
	}

	// 6. 将两区间剩余到值添加到临时数组中
	for i <= mid {
		tmp[k] = q[i]
		i++
		k++
	}
	for j <= r {
		tmp[k] = q[j]
		j++
		k++
	}
	// 7. 将临时数组中的值，放回原数组
	for i, j := l, 0; i <= r; i, j = i+1, j+1 {
		q[i] = tmp[j]
	}
}

查找

整数二分

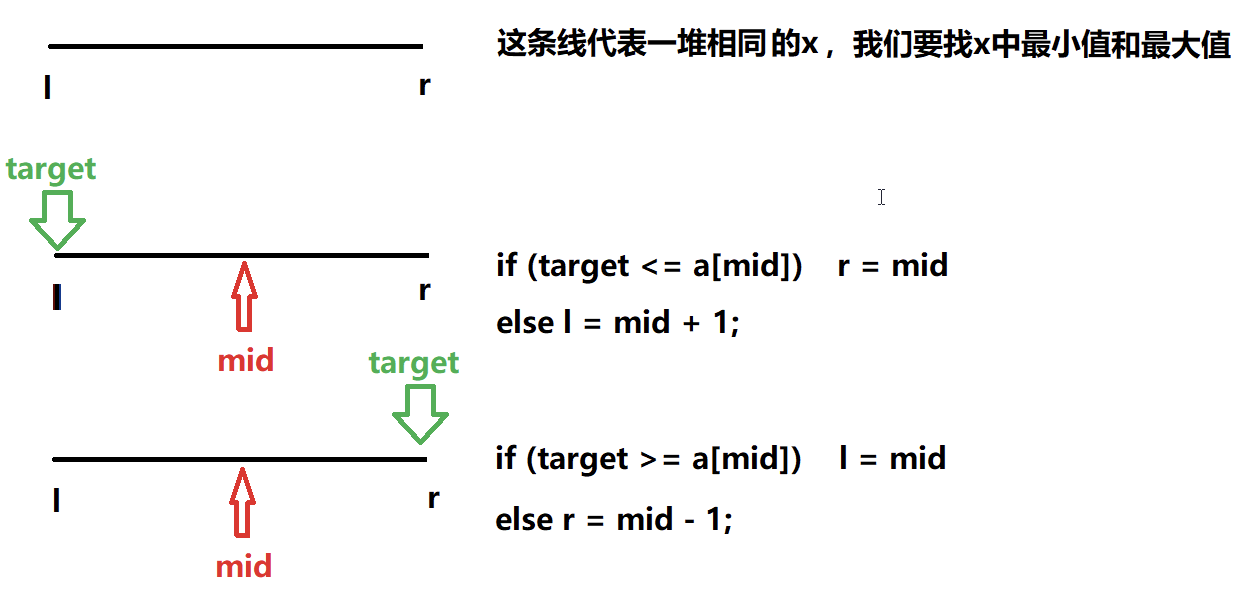
整数二分算法模板 —— 模板题

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

题意：

升序整数数组，查找元素k的起始位置和终止位置（位置从 0 开始计数）

思路：

当题目满足，左右两个区间，一边满足一边不满足时，查找值，可以使用二分查找。

通过检查x是否满足某种性质，来确定边界点

解法：

二分

package main

import "fmt"

// 题意：升序整数数组，查找元素k的起始位置和终止位置（位置从 0 开始计数）
func main() {
	// var n, k int
	// fmt.Scanf("%d%d", &n, &k)
	// var q = make([]int, n)
	// for i := 0; i < n; i++ {
	// 	fmt.Scanf("%d", &q[i])
	// }
	k := 3
	q := []int{1, 2, 2, 3, 3, 4}
	x := []int{5, 4, 3}
	for ; k > 0; k-- {
		fmt.Println(x[k-1])
		l := bsearch_1(q, x[k-1])
		r := bsearch_2(q, x[k-1])
		fmt.Printf("%d %d\n", l, r)
	}
}

func bsearch_1(q []int, x int) int {
	l, r := 0, len(q)-1
	for l < r{
		mid:=(l+r)>>1
		if q[mid]	>= x{
				r = mid	
		}else {
				l = mid + 1
		}
	}
	if q[l] != x {return -1}
	return l
}

func bsearch_2(q []int, x int) int {
	l, r := 0, len(q)-1
	for l < r {
		mid:=(l+r+1) >> 1
		if q[mid] <= x {
			l = mid
		}else{
			r = mid -1
		}
	}
	if q[l] != x {return -1}
	return l
}

高精度

加法

package main

import (
	"fmt"
	"strconv"
)

func main() {
	var a, b string
	fmt.Scan(&a, &b)

	var (
		aSlice = make([]int, 0)
		bSlice = make([]int, 0)
	)
	// 1.大整数存储到数组
	// 倒着存储，低位表示个数，高位表示大数
	// eg. "123456"   ==>   {[6],[5],[4],[3],[2],[1]}
	for i := len(a) - 1; i >= 0; i-- {
		v, _ := strconv.Atoi(string(a[i]))
		aSlice = append(aSlice, v)
	}

	for i := len(b) - 1; i >= 0; i-- {
		v, _ := strconv.Atoi(string(b[i]))
		bSlice = append(bSlice, v)
	}

	// 2.相加  模拟人工相加
	cSlice := add(aSlice, bSlice)
	// 3. 打印结果
	for i := len(cSlice) - 1; i >= 0; i-- {
		fmt.Printf("%d", cSlice[i])
	}
	fmt.Println()
}

// 每一位数为 Ai+Bi+t
func add(a, b []int) (c []int) {
	t := 0 //进位
	for i := 0; i < len(a) || i < len(b); i++ {
		if i < len(a) {
			t += a[i]
		}
		if i < len(b) {
			t += b[i]
		}
		c = append(c, t%10)
		t /= 10
	}
	if t > 0 {
		c = append(c, t)
	}
	return
}

减法

package main

import (
	"fmt"
	"strconv"
)

func main() {
	var a, b string
	fmt.Scan(&a, &b)

	var (
		aSlice = make([]int, 0)
		bSlice = make([]int, 0)
		cSlice []int
	)
	// 1.大整数存储到数组
	// 倒着存储，低位表示个数，高位表示大数
	// eg. "123456"   ==>   {[6],[5],[4],[3],[2],[1]}
	for i := len(a) - 1; i >= 0; i-- {
		v, _ := strconv.Atoi(string(a[i]))
		aSlice = append(aSlice, v)
	}

	for i := len(b) - 1; i >= 0; i-- {
		v, _ := strconv.Atoi(string(b[i]))
		bSlice = append(bSlice, v)
	}

	// 2.比较两个值的大小
	if cmp(aSlice, bSlice) { //a>b
		cSlice = sub(aSlice, bSlice)
		// 3. 打印结果
		for i := len(cSlice) - 1; i >= 0; i-- {
			fmt.Printf("%d", cSlice[i])
		}
	} else { //b>a
		cSlice = sub(bSlice, aSlice)
		// 3. 打印结果
		fmt.Print("-")
		for i := len(cSlice) - 1; i >= 0; i-- {
			fmt.Printf("%d", cSlice[i])
		}
	}

	fmt.Println()
}

// c = a - b
func sub(a, b []int) (c []int) {
	// t 进位
	//Ci=Ai-Bi-t
	for i, t := 0, 0; i < len(a); i++ {
		t = a[i] - t
		if i < len(b) {
			t -= b[i]
		}
		// 为什么 (t+10)%10
		// a-b = t
		// 如果 t> 0 结果为  t
		// t<0  结果为  t+10
		// 两者相结合  (t+10)%10
		// eg. 22-13 ==>   2 - 3 <0,向前借一位  ==> 12-3=9 相等于 （-1+10）%10=9
		c = append(c, (t+10)%10)
		if t < 0 { //证明向前借了一位
			t = 1
		} else {
			t = 0
		}
	}
	for len(c) > 1 && c[len(c)-1] == 0 {
		c = c[:len(c)-1]
	}
	return
}

// 判断 a>=b
func cmp(a, b []int) bool {
	if len(a) != len(b) {
		return len(a) > len(b)
	}
	for i := len(a) - 1; i >= 0; i-- {
		if a[i] != b[i] {
			return a[i] > b[i]
		}
	}
	return true
}

MiHuaaaaaaaa/acwing

基础算法

排序

快速排序

归并排序

查找

整数二分

高精度

加法

减法