LieTorch: Tangent Space Backpropagation
Introduction
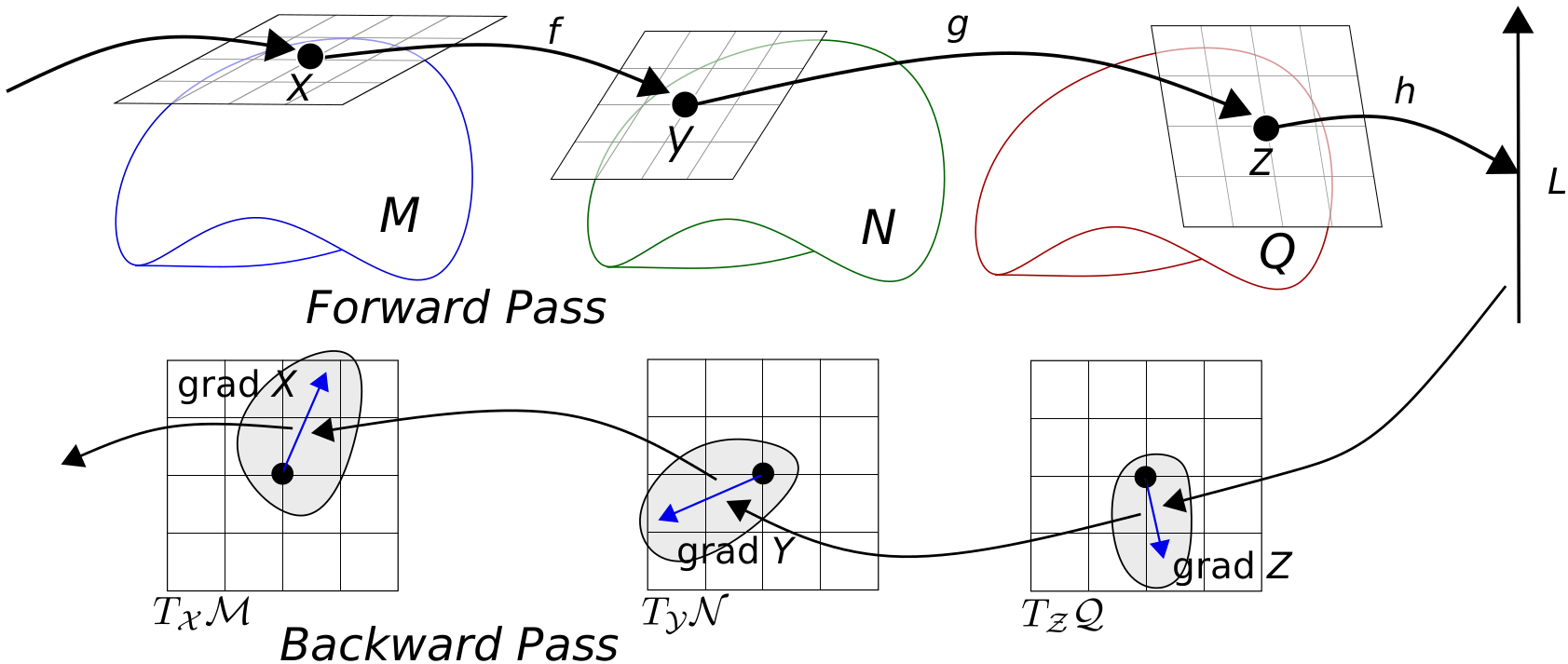
The LieTorch library generalizes PyTorch to 3D transformation groups. Just as torch.Tensor is a multi-dimensional matrix of scalar elements, lietorch.SE3 is a multi-dimensional matrix of SE3 elements. We support common tensor manipulations such as indexing, reshaping, and broadcasting. Group operations can be composed into computation graphs and backpropagation is automatically peformed in the tangent space of each element. For more details, please see our paper:
Tangent Space Backpropagation for 3D Transformation Groups
Zachary Teed and Jia Deng, CVPR 2021
@inproceedings{teed2021tangent,
title={Tangent Space Backpropagation for 3D Transformation Groups},
author={Teed, Zachary and Deng, Jia},
booktitle={Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
year={2021},
}
Installation
Requirements:
- Cuda >= 10.1 (with nvcc compiler)
- PyTorch >= 1.8
We recommend installing within a virtual enviornment. Make sure you clone using the --recursive flag. If you are using Anaconda, the following command can be used to install all dependencies
git clone --recursive https://github.com/princeton-vl/lietorch.git
cd lietorch
conda create -n lie_env
conda activate lie_env
conda install scipy pyyaml pytorch torchvision torchaudio cudatoolkit=10.2 -c pytorch
To run the examples, you will need OpenCV and Open3D. Depending on your operating system, OpenCV and Open3D can either be installed with pip or may need to be built from source
pip install opencv-python open3d
Installing (from source)
Clone the repo using the --recursive flag and install using setup.py (may take up to 10 minutes)
git clone --recursive https://github.com/princeton-vl/lietorch.git
python setup.py install
./run_tests.sh
Installing (pip)
You can install the library directly using pip
pip install git+https://github.com/princeton-vl/lietorch.gitOverview
LieTorch currently supports the 3D transformation groups.
| Group | Dimension | Action |
|---|---|---|
| SO3 | 3 | rotation |
| RxSO3 | 4 | rotation + scaling |
| SE3 | 6 | rotation + translation |
| Sim3 | 7 | rotation + translation + scaling |
Each group supports the following differentiable operations:
| Operation | Map | Description |
|---|---|---|
| exp | g -> G | exponential map |
| log | G -> g | logarithm map |
| inv | G -> G | group inverse |
| mul | G x G -> G | group multiplication |
| adj | G x g -> g | adjoint |
| adjT | G x g*-> g* | dual adjoint |
| act | G x R^3 -> R^3 | action on point (set) |
| act4 | G x P^3 -> P^3 | action on homogeneous point (set) |
| matrix | G -> R^{4x4} | convert to 4x4 matrix |
| vec | G -> R^D | map to Euclidean embedding vector |
| InitFromVec | R^D -> G | initialize group from Euclidean embedding |
Simple Example:
Compute the angles between all pairs of rotation matrices
import torch
from lietorch import SO3
phi = torch.randn(8000, 3, device='cuda', requires_grad=True)
R = SO3.exp(phi)
# relative rotation matrix, SO3 ^ {8000 x 8000}
dR = R[:,None].inv() * R[None,:]
# 8000x8000 matrix of angles
ang = dR.log().norm(dim=-1)
# backpropogation in tangent space
loss = ang.sum()
loss.backward()Converting between Groups Elements and Euclidean Embeddings
We provide differentiable FromVec and ToVec functions which can be used to convert between LieGroup elements and their vector embeddings. Additional, the .matrix function returns a 4x4 transformation matrix.
# random quaternion
q = torch.randn(1, 4, requires_grad=True)
q = q / q.norm(dim=-1, keepdim=True)
# create SO3 object from quaternion (differentiable w.r.t q)
R = SO3.InitFromVec(q)
# 4x4 transformation matrix (differentiable w.r.t R)
T = R.matrix()
# map back to quaterion (differentiable w.r.t R)
q = R.vec()Examples
We provide real use cases in the examples directory
- Pose Graph Optimization
- Deep SE3/Sim3 Registrtion
- RGB-D SLAM / VO
Acknowledgements
Many of the Lie Group implementations are adapted from Sophus.