After knowing how to use api of opencv, including calibrating and undistorting, i wanted to figure out how
the undistorting process work. So i viewed http://paulbourke.net/dome/fisheye/ and learnt projection from
image to hemisphere surface, and wrote undistorting in my own way.
实现了从标定板标定参数, 到校正单张图片, 视频文件和视频流
First my input datas of calibrateing chessboard will locate corner points, then give those points to fisheye
calibrating of opencv which based on Zhengyou Zhang's 1999 paper , this will measure internal and external
parameters, and distortion coefficients. So you can use those parameters
to remap every pixels.
I already have wrote functions including undistorting image data, video data and stream.
实现任意大小图片, 以图片中心为畸变中心, 可以任意扩张输出大小.
后续可能会添加畸变参数和任意位置畸变中心.
根据Paul的网页我们能知道平面到半球上的映射, 当然这只是一半, 还需要将半球上的坐标重新映射到输出平面.
By following Paul's web, first you'd better consider every pixels with polar coordinates and sphere coordinates,
using length and angle to describe pixels, then you can easily calculate whole projection. To undistort,
all you need to do is to make every coordinates on hemisphere map to the new plane - your output plane.
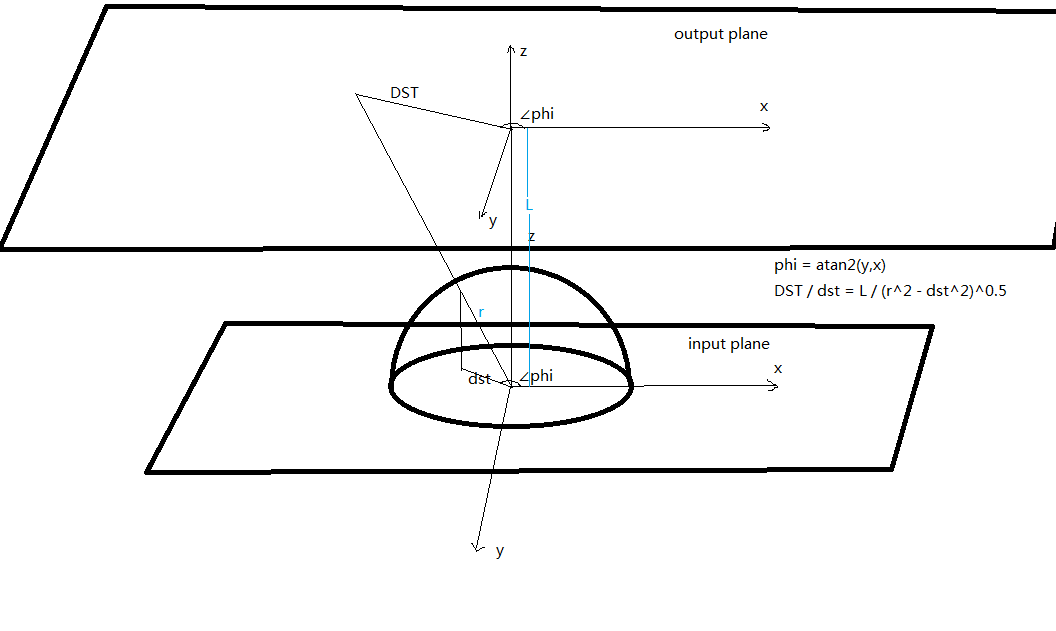
由上图可知反畸变其实就是将输入图像input平面上坐标映射到新平面output上, 利用极坐标系和相似三角形(不需要球坐标系的theta).
一般我们已知r和L(r是镜头半径, L是input和output平面的距离, 一般情况下r等于L), 则利用图上中关系式可求每一点坐标前后映射.
We can easily knowing what we actually want is phi and distance to the center of one point, using similar
rectangle you can transform distance to center on output plane and input plane (this actually uses angle theta),
and both output plane and input plane have same phi.
I wrote three version : without interpolation, with interpolation and optimizing with matrix. Dealing gray
images only, and i didn't consider distorting parameters, maybe i will add it in future. I only upload last two
version.
Input:

Outputs in three way:
实际上真正从原图映射到输出图像的原始数据是会像下面这张无插值的输出, 黑色的空缺通过插值算法填充 :
Without interpolation :

线性插值 :
Linear interpolation :

矩阵加速, 由于矩阵运算的局限性, 在边缘区域所有扩展都是边缘拉伸, 但是不影响上图一样的有效区域内变化 :
Speed up by using mtrix :

代码里有两个版本, 前一个遍历每一pixel进行插值和映射, 后一个利用矩阵加速, 在我的数据和设备能上提升43倍, 满足实时处理.
Every 640*480 image on my very old computer using second way cost 17.25s, and the last way cost 0.395s, speed
up for 4300%