Wavefront Algorithm for Optimal Trajectory Planning in a 2D Environment with Obstacles
Overview
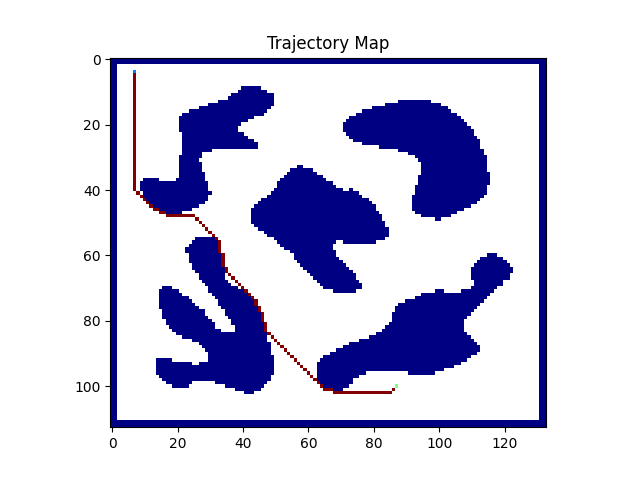
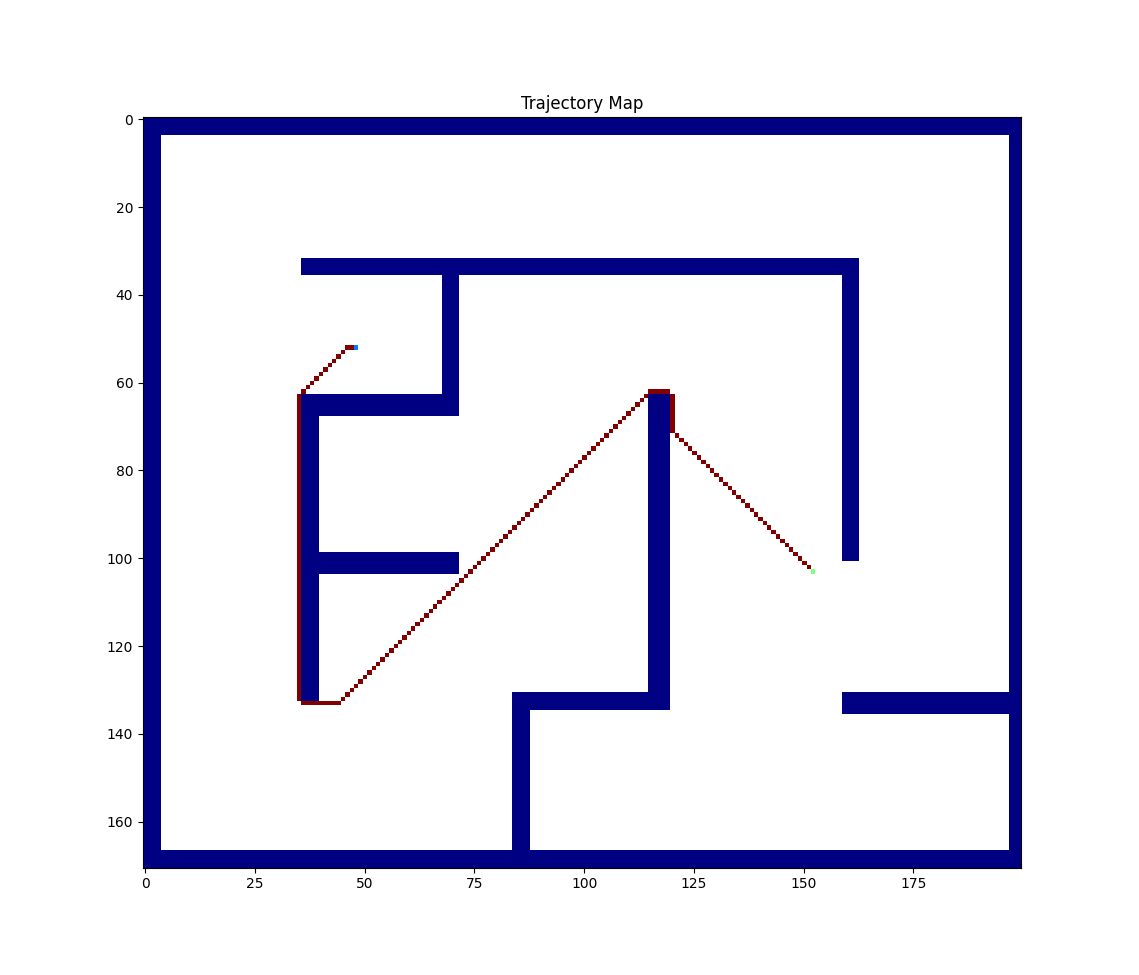
This project aims to develop a solution for finding the optimal trajectory towards a goal in a 2D environment that is closed by obstacles. The proposed approach utilizes the Wavefront Algorithm, a popular pathfinding algorithm that effectively navigates through complex environments.
Args
python main.py [.mat file path] [variable name]Input
Please, Enter X coord. for start: 100
Please, Enter Y coord. for start: 100
Output
value_map =
[[1. 1. 1. ... 1. 1. 1.]
[1. 1. 1. ... 1. 1. 1.]
[1. 1. 1. ... 1. 1. 1.]
...
[1. 1. 1. ... 1. 1. 1.]
[1. 1. 1. ... 1. 1. 1.]
[1. 1. 1. ... 1. 1. 1.]]
trajectory =
100 100
99 100
98 100
97 100
......
......
......
100 149
101 150
102 151
103 152
Time taken: 6.2487 secs
Dependencies
scipy
numpy
matplotlib
timeWavefront Algorithm
Given the start point and the goal point, the algorithm is implemented as follows:
- The goal point is initialized with 2
- The neighboring cells to the goal that are not obstacles are assigned the value of the goal point + 1
- Update the goal value, that is, goal = goal + 1 then repeat steps 1 & 2 until all the spaces are filled.
- The trajectory (shortest distance to the goal) is easily found by taking differences with all neighboring cells, that is, the minimum of the neighboring cells.