Next Steps: coords.py is great but it doesn't use the H9 class yet - it was my earliest file, and it needs refactoring. It should be straightforward - I will have to consider how best to map the integrate the regions into Fuller/Snyder equilaterals. My guess is that it should be fine, as long as I consider the boundaries correctly.
Also, I want to show off using large hexes where there isn't much data (represented by colour) to demonstrate good hierarchic control. The actual drawing/placement tools are in -but not being exploited to show them off.
Distance management, etc, including neighbours, have not yet been implemented. Documentation on district identity could be far better.
News:
New hierarchic drawing getting better, and everlasting hexes is a thing.
Hierarchic Labels are working.
The project is centred on the idea of hierarchic hexagonal grids, while keeping the number of polygons to a minimum. Also - do not be surprised if you find bugs! This is still very much a work in progress!
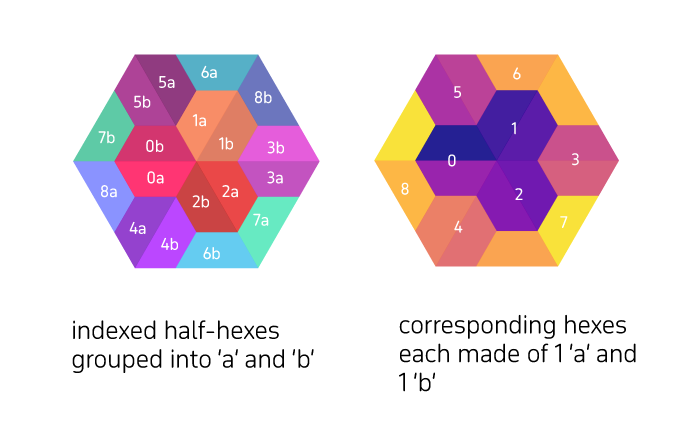
My solution to this quandary is to use half-hexagons ('regular' trapezoids composed of three equilateral triangles) as the primary fundamental. This can be used in a vertex centred / offset 'H9 aperture', where any hexagon can be subtended into 9 smaller hexagons, albeit with three hexagons shared directly along the half-hex line. ('Apertures' normally remain shape centred. Here we do not do that.)
My past research was based on something very similar to the H3 methods currently funded by Uber (the ride company).
This is auxiliary to the work that has been done by many others, including Buckminster Fuller, and Snyder at Oregon University, regarding hex grids in general, as well as discrete global grids (ISEA DGGs), but my focus is more on general 2D grids, rather than just global mapping - also, the grid I use here is vertex centred, whereas most research has been developed on hexagon-centred hierarchic grids. H9 is “only” a left half-shifted Aperture 9 But what makes it special (to me) is that the overlapping hexes only share two parents, not three - the cost being steep enough: no central hex, and an extra overlapped hex. But the advantage is that no matter how high in the hierarchy one goes, one never splits a hexagon into anything more than a half, and only hexagons '6', '7', '8' (districts 12/13, 14/15, 16/17 respectively) ever get sliced in half.
Below is the basic unit hexagon, showing it's division into the 18 half-hexagons that compose it. The numbering is one way of indexing the half-hexagons.
The plane can be tiled using the following:
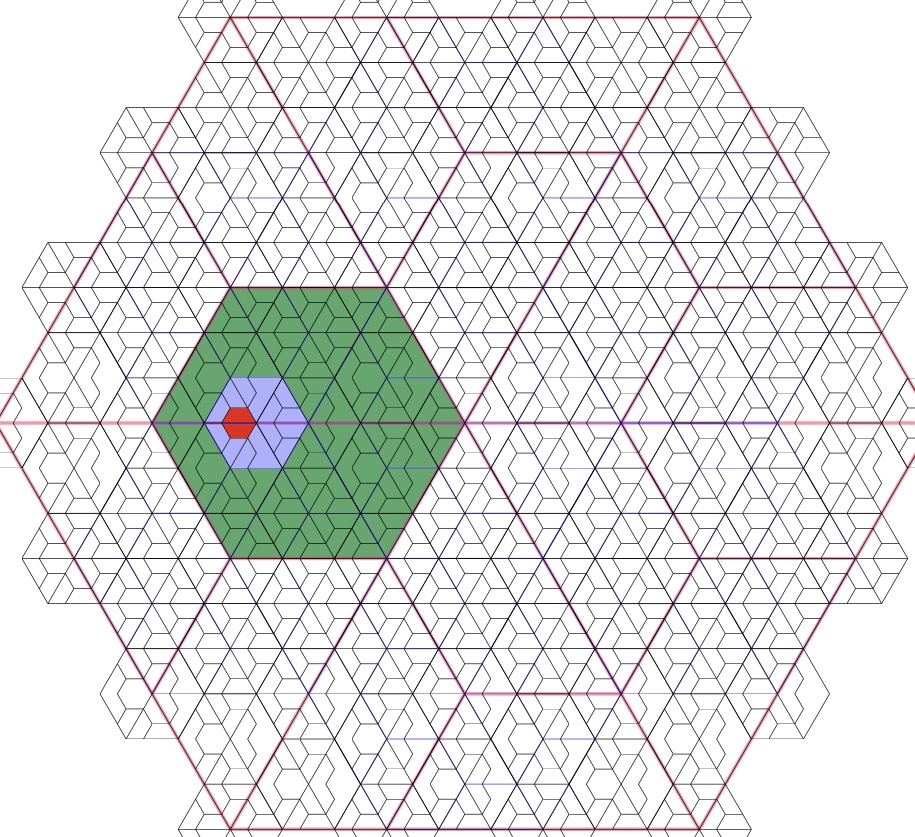
A hexagonal grid hierarchy can be seen below, with the outer hexagon in white, then the successive lower hierarchies in green, blue and red. The hierarchy is unlimited in depth.
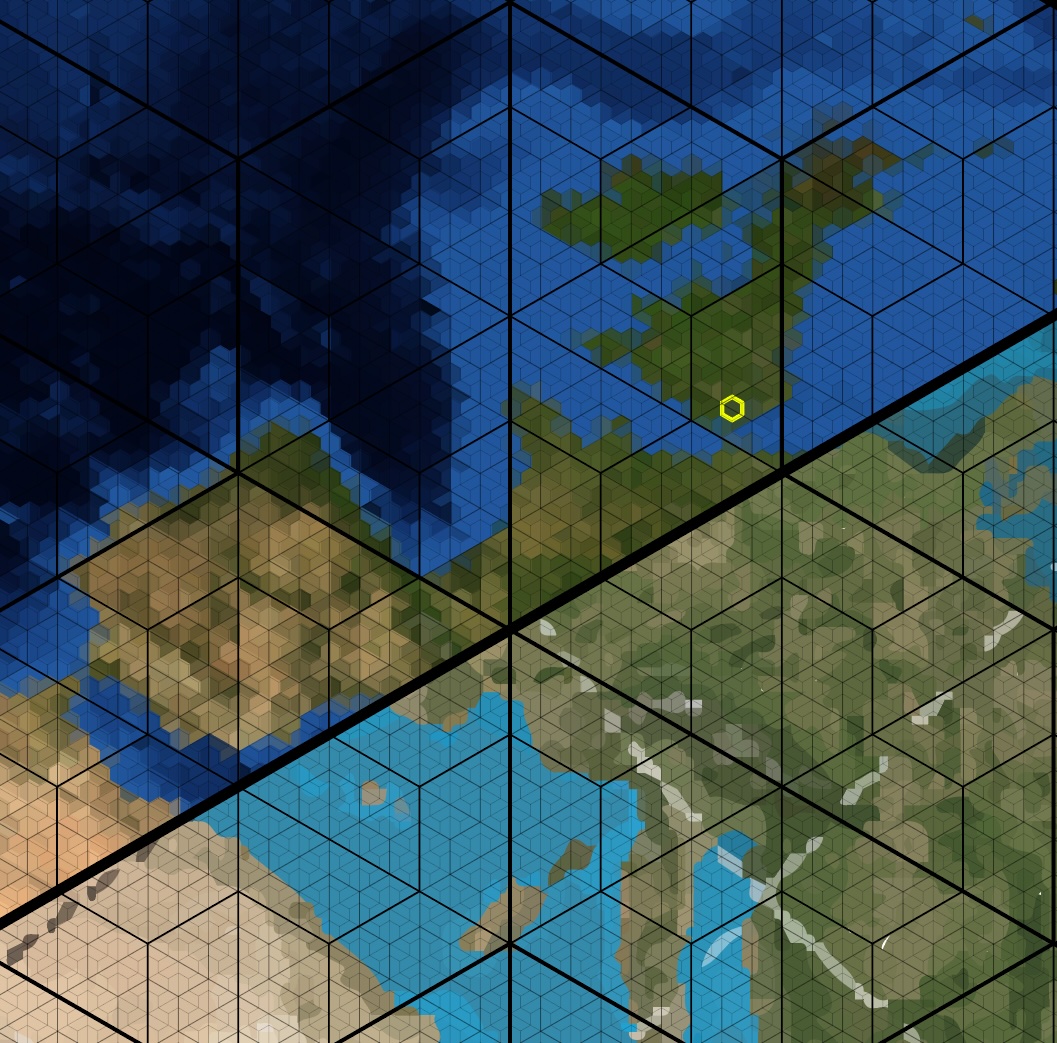
This method can be used on any map projection - ad it is a space partitioning mechanism rather than a projection, but it lends itself particularly well to the Dymaxion (and similar) icosahedral maps. Here one can see my hometown (London) marked out in yellow. What is stunning is that for every hexagon at a given hierarchy for Dymaxion, the area is always the same.
Grid referencing. Likewise, we can use an address system that resolves hierarchy and location extremely easily. One thing that I like is that we can use subtended regions rather than axis-oriented addresses. Why is that nice? It offers a few benefits
- first of all there is only one string (unlike, EG lat/long or OS grids - which still confuse those not familiar with ), and where locality can be kept relevant without having to consider a remote origin.
Another 'feature', is that from any given root, the length of the address tells us about the level of hierarchy. Moreover, merely by shortening the address, we may derive the parent.
Grid coordinates are best done, for this, using base 9, and using a signifier for the half-hex specialisation. One can work out the entire half-hex address from a given hex address - but it does require following some rules.
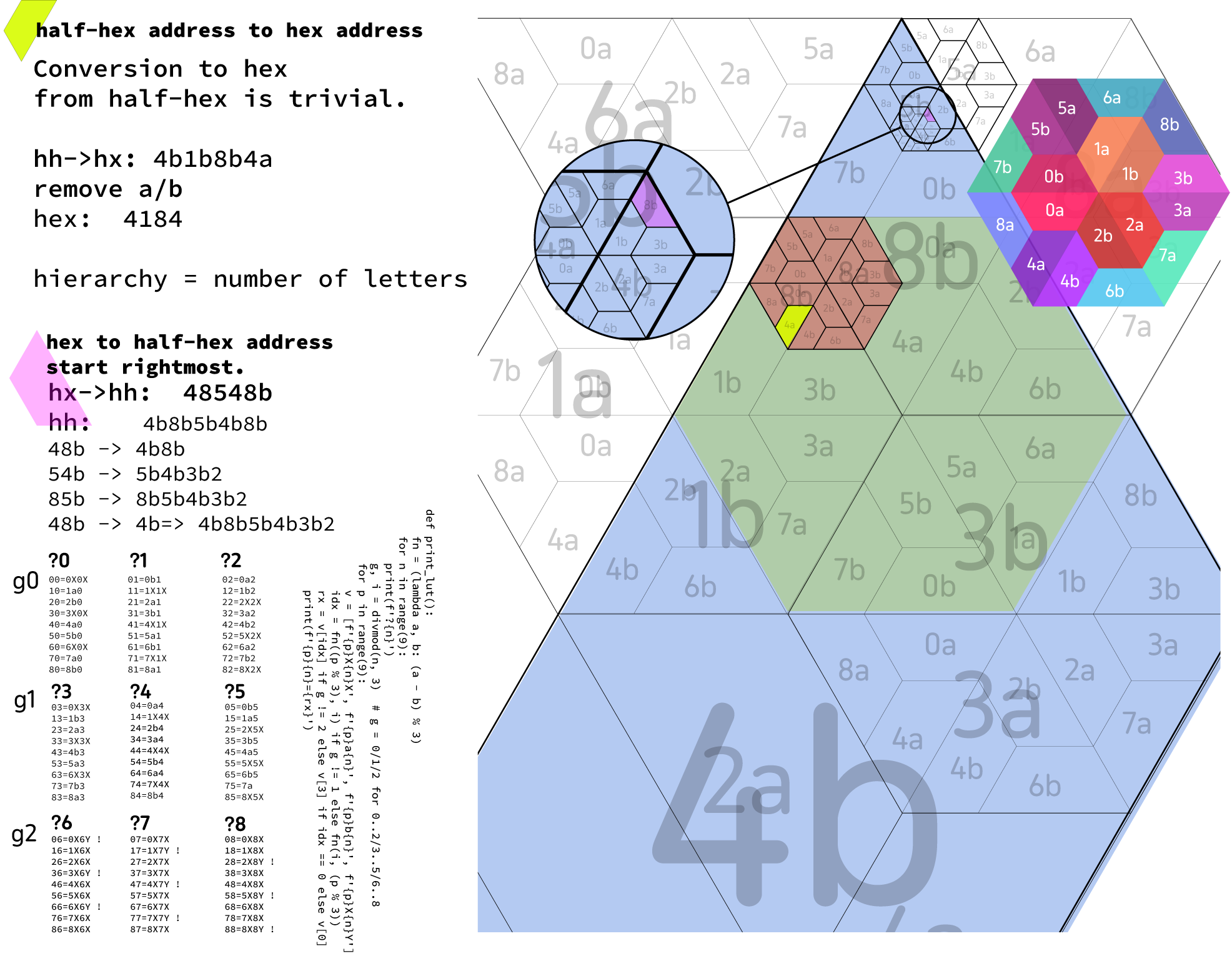Here we see a hierarchic grid addressing system. The 'a/b' of each half-hex could be replaced with
symbols (I currently show the 'a' address, and leave the 'b' blank - 2 explicit characters are not necessary - and maybe the 'a' could be handled with just a '+'), but the point is that we only need to store the final half-hex place (when we have one), as
we can derive the ancestral half-hexagons according to the address we are given.
For example, an address 318705251a, even though it only refers by hexagon address (+the final half-hex), can be reliably decomposed to it's full-half-hex address (3b1a8a7a0b5a2a5a1a) - which is sort of magical (to me anyhow). Needless to say, it also identifies the entire hierarchy, and likewise the depth of this address (9). In terms of spatial coordinates, such a 10-character address provides a location (if we are using the entire surface of the world, on an equal area projection) to a patch of earth consistently 658 square metres in area – a resolution of just over 80 metres. (for contrast, Lat/Long require 2x 3 decimal places on top of the degrees for that, and give an inconsistent areas that depend on how close one is to the equator, being non-equal area projection of course).