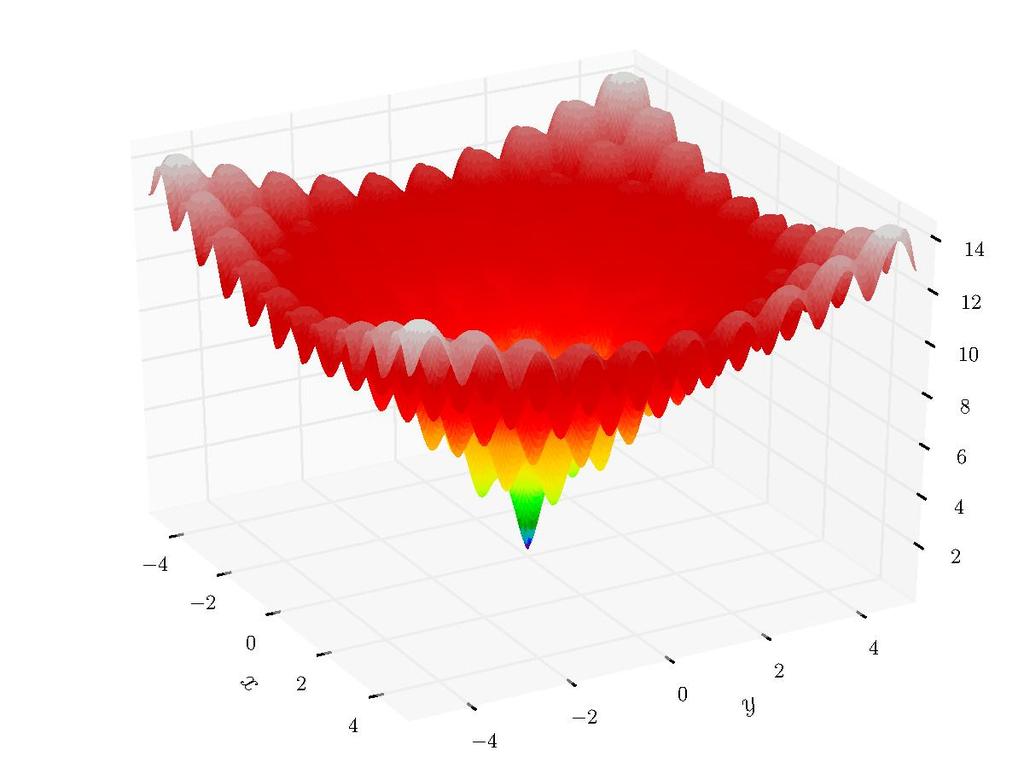
This project contains an implementation of a hill-climbing algorithm as well as a differential evolution algorithm applied to the Ackleys function.
Ackley's function is a function used for testing local optimization algorithms. It has a large number of local minima and one global min at (0, 0)
This function works as follows:
- Randomly generates an initial position (x, y) in the range (-5, 5)
- Check the value of the Ackley's function f(x, y)
- Generate a new position (x', y'):
- x' = ((rand()) - 0.5) * 0.1 + x
- y' = ((rand()) - 0.5) * 0.1 + y
- Compute f(x', y')
- Continue this process until a better position is not found in the last 100 steps
- Run this whole process 100 times
This function works as follows:
- Initializes its parameters.
- Np = 20
- Nc = 100
- Cr = 0.1
- F = 0.8
- Initializes its population of agents
- Selects a candidate agent, currentAgent, from the list.
- Also randomly selects 3 other agents a, b, c, none of which can be the same or equal to currentAgent
- Computes the mutant vector V = a + F(b-c)
- Generates a random number rand from [0-1)
- Checks to see if rand < Cr for each coordinate in the agent. If it is, swap the coordinate with the mutant vector
- If Ackleys(mutantAgent) < Ackleys(currentAgent) set currentAgent to the mutant
- When this has been done Nc times, find the best point and return it