A Secure Sum Protocol for Privacy Preserving ML
When multiple parties, each owning a privacy-sensitive dataset, would like to collectively perform analytics on the union of the datasets - problems may arise regarding data privacy and security concerns of each individual party. Current commercial solutions require each party to share their raw data or local aggregates with a trusted third party or a mediator under an appropriate confidential agreement, and have the mediator compute and share the results.
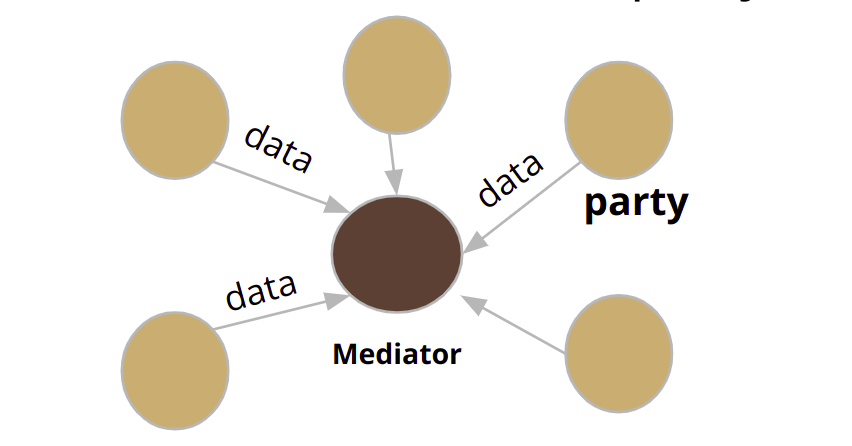
But what if the mediator is not trustworthy?
To address this problem, we are introducing a generalized framework that enables training of machine learning models on multi-party, distributed data in a privacy-preserving manner. The proposed framework assumes an untrusted mediator. Under our framework, each party shares only encrypted local results, and then the mediator aggregates these results to obtain the global result.
Our main contributions would be the following :
-
Developing two secure gradient descent algorithms - one for horizontally partitioned data and another for vertically partitioned data. They are generic and apply to a wide class of machine learning problems such as regression, classification and clustering.
-
Implementing and testing the proposed solution for three analytic use-cases : linear regression, logistic regression and support vector machine, using both real-world and synthetic datasets.
-
Evaluating the performance of the proposed approach in terms of accuracy of the resulting model, communication cost, and latency, and compare it with two baseline approaches - centralized and distributed trusted mediator.
- Shagufta Mehnaz, Gowtham Bellala, and Elisa Bertino. 2017. A Secure Sum Protocol and Its Application to Privacy-preserving Multi-party Analytics. In Proceedings of SACMAT’17, June 21–23, 2017, Indianapolis, IN, USA. DOI: http://dx.doi.org/10.1145/3078861.3078869
- Protocol Description
The following is the list of our assumptions on the parties and the mediator:
-
Each party and the mediator has a secret key and a public key. The public keys of all parties and the mediator are known to all entities.
-
The encryption and decryption operations performed by the parties always follow a particular order.
-
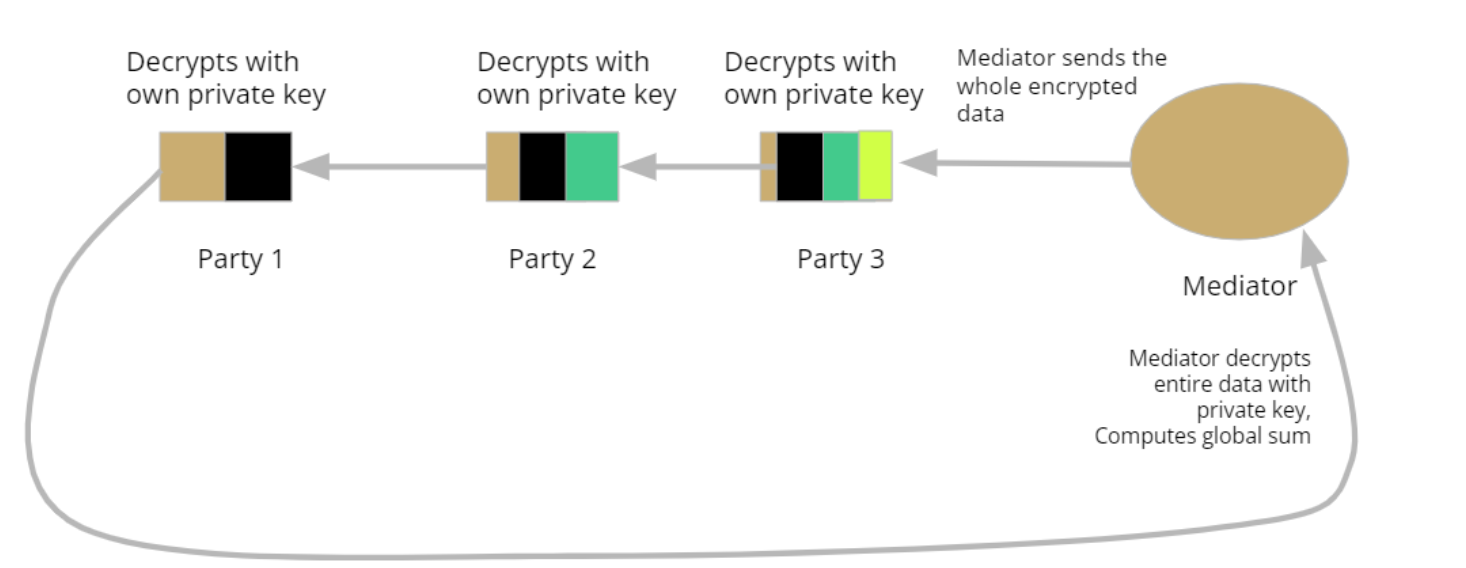
The protocol consists of three stages: input preparation, anonymization and sum calculation. The first phase involves the preparation of input values by each party, which includes dividing the values into segments and recursively encrypting them using the public keys of the mediator and the N parties. In the second phase, the Nth party performs decryption and reshuffling of the segments, passing them on to the N-1th party, and so on, until the 1st party. This results in the anonymization of the segments, with only one layer of encryption remaining with the mediator's key. Finally, in the third phase, the mediator decrypts the segments using their secret key and calculates the sum.
The protocol is depicted in the following diagrams (Fig 1 and 2)
Let’s assume, there are i = 1,2,3, …, N parties. Available data to each party is Si.
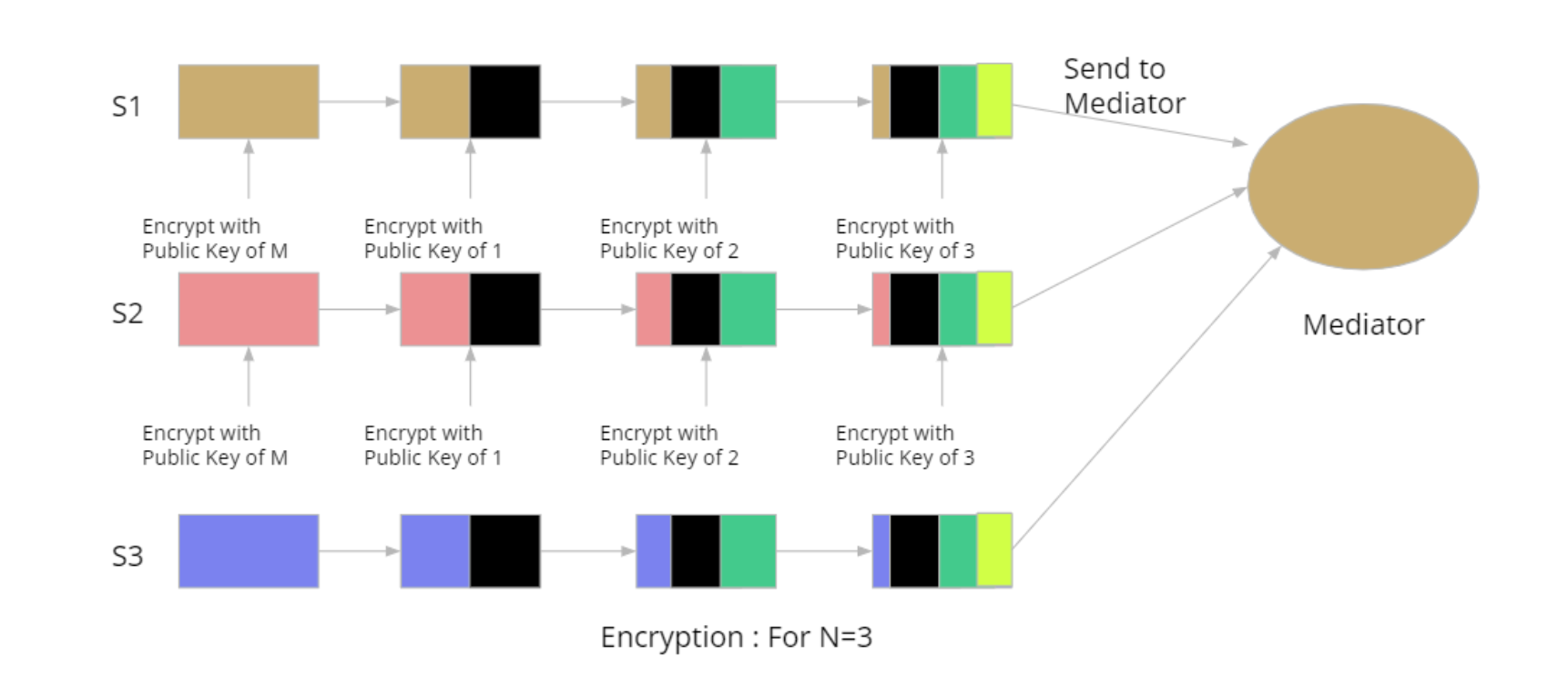
Fig 1 : Step 1- Encryption with Elgamal Cryptosystem
Fig 2 : Step 2- Decryption
- Applying Protocol to Gradient Descent Algorithm Most machine learning algorithms can be formulated as an optimization problem, with the goal of minimizing a cost (or objective) function. Also, most optimization problems rely on gradient descent.
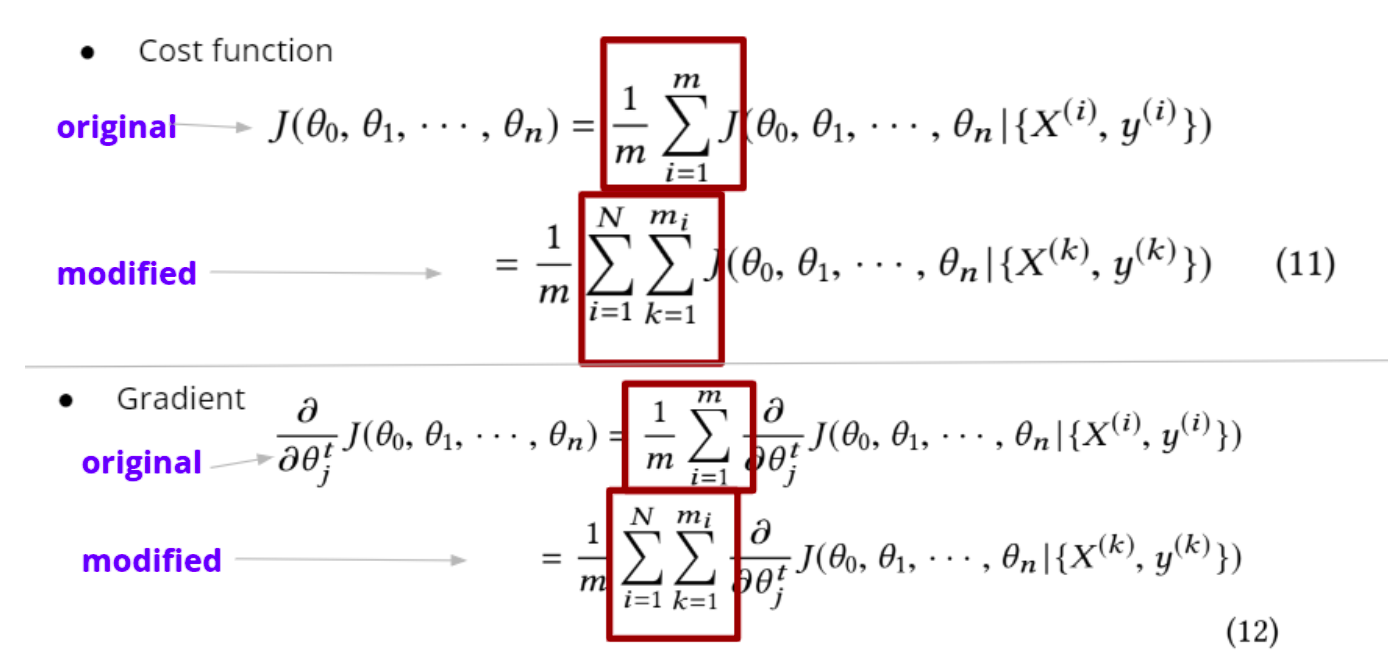
Fig 3 : Modifications in Gradient Descent to Implement Secure Sum
- Created a distributed systems scenario with Docker.
- 3 computers (container names : client1, client2, client3)
- A mediator (container name : server)
- All containers are connected via a bridge network.
- Implemented secure sum protocol for these containers. For encryption algorithm, we used RSA cryptosystem.
- Implemented logistic regression for three scenarios :
- Centralized Trusted : Regular logistic regression on entire train set, without any partitioning.
- Distributed Trusted : Logistic regression on nodes on which the dataset is horizontally partitioned. Here, each node computes gradients locally and sends them to the server unencrypted. After receiving all the gradients, the server updates the weights and sends them back to each node.
- Distributed Untrusted : Similar to distributed trusted, here each of the nodes has a horizontal partition of the dataset. Each node computes gradients locally and sends to the server after encrypting them, following the secure sum protocol. After receiving all the gradients, the server updates the weights and sends them back to each node.
- Trained and tested logistic regression for each scenario, using the dataset SUSY. A total of 10000 entries of the shuffled dataset was taken, and the train and test set were generated by an 80-20 split. The hyperparameters of the model were kept the same across scenarios.
- Computed accuracy, precision, recall and latency (time to train and generate predictions) for all three scenarios.
- Install Docker on your Ubuntu machine. To install Docker on Ubuntu, you can follow these steps:
-
Update the apt package index:
`sudo apt-get update` -
Install the dependencies necessary to use Docker:
`sudo apt-get install apt-transport-https ca-certificates curl gnupg lsb-release` -
Add the Docker GPG key:
`curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo gpg --dearmor -o /usr/share/keyrings/docker-archive-keyring.gpg` -
Add the Docker repository to APT sources:
`echo "deb [arch=amd64 signed-by=/usr/share/keyrings/docker-archive-keyring.gpg] https://download.docker.com/linux/ubuntu $(lsb_release -cs) stable" | sudo tee /etc/apt/sources.list.d/docker.list > /dev/null` -
Update the apt package index again:
`sudo apt-get update` -
Install Docker:
`sudo apt-get install docker-ce docker-ce-cli -
Verify that Docker is installed correctly by running the "hello-world" container:
`sudo docker run hello-world` -
This should download and run a small Docker container, and output a message that says "Hello from Docker!" if everything is working correctly.
-
Note: You may need to run some of these commands with sudo or as a privileged user, depending on your system configuration.
By default, running Docker commands requires sudo privileges. To run Docker commands without using sudo, you can add your user to the docker group, which grants permission to manage Docker as a non-root user.
To add your user to the docker group, follow these steps:
Open a terminal window and enter the following command to add your user to the docker group:
`sudo usermod -aG docker ${USER}`
Replace ${USER} with your username.
To apply the group membership changes, log out and back in, or run the following command:
`newgrp docker`
This command refreshes your group membership without requiring a log out and back in.
Verify that you can run Docker commands without sudo by running the "hello-world" container:
`docker run hello-world`
If everything is working correctly, you should see output similar to this:
`Hello from Docker!`
This message shows that your installation appears to be working correctly.
-
Run build.sh to create the environment.
chmod +x build.sh ./build.sh
You only need to do this once.
-
Run the following commands to simulate each three scenarios :
python3 centralized_trusted.py ./distributed-trusted.sh ./distributed-untrusted.sh
-
build.sh
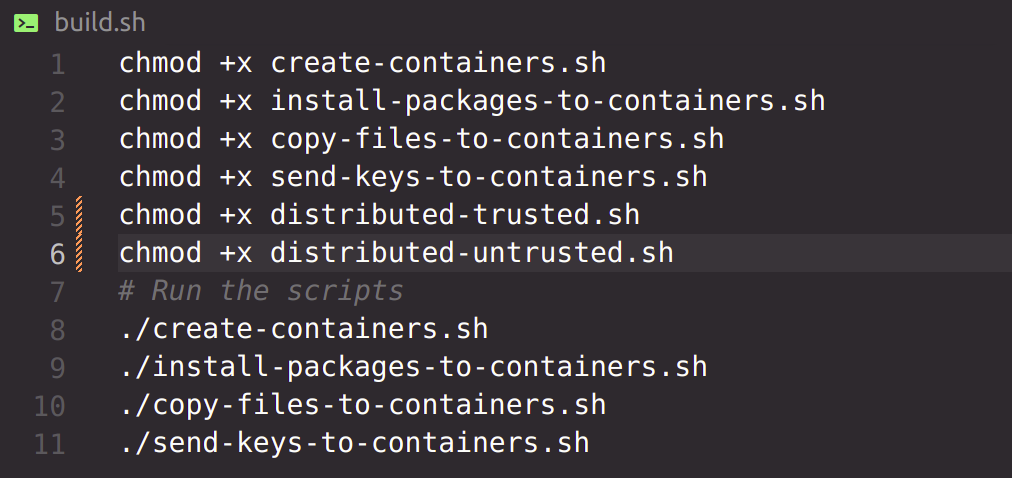| ---- create-containers.sh| ---- install-packages-to-containers.sh
| ---- copy-files-to-containers.sh
sends all the scripts needed to run locally on each computer, such as rsa implementation, logistic regression etc.
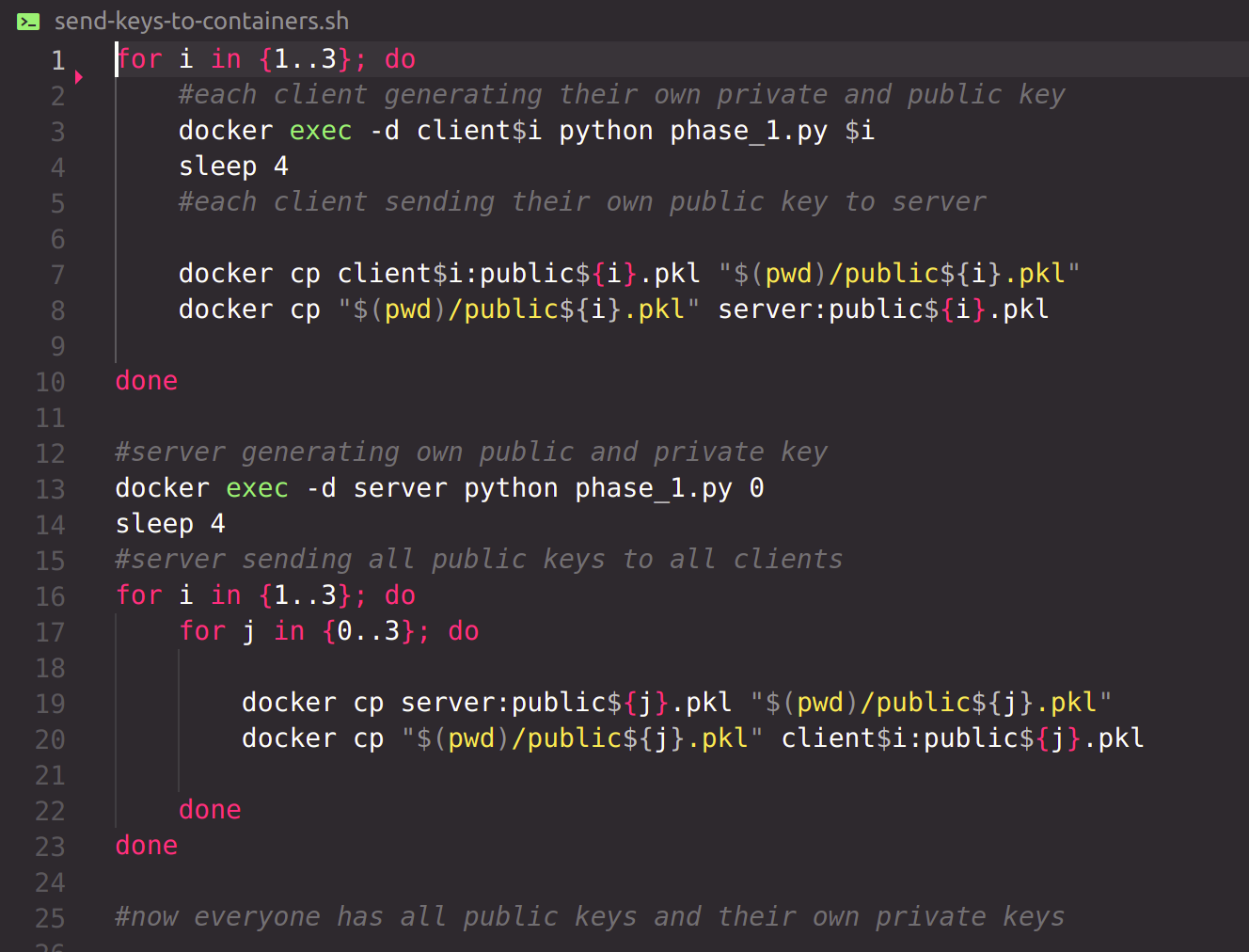
| ---- send-keys-to-containers.sh
Generates private and public key of each container and sends the public keys to every container.
- | ----------------- phase_1.py generates private and public key of each client and server and then stores them in pickle files locally.
Now everyone has all necessary local scripts, all public keys and their own private keys.
- centralized_trusted.py Basic logistic regression performed on the entire dataset, on a central system, without any partitioning.
|-----logreg.py
|-----logreg_client.py
|-----logreg_server.py
|-----logreg_client_inference.py
Restart containers if needed:
Remove any previous loss, gradient or parameters file:
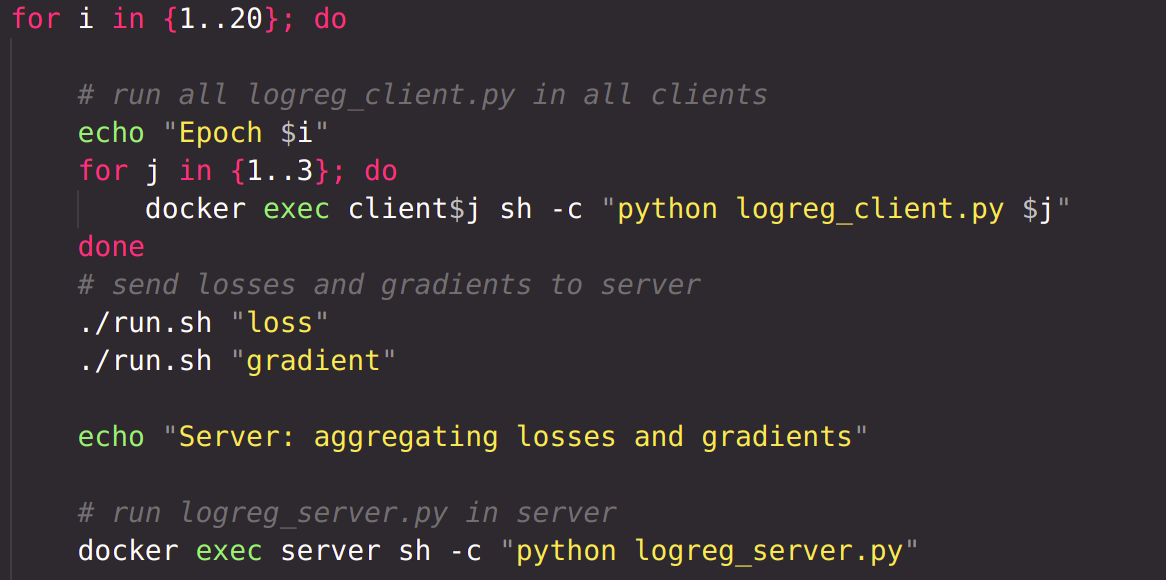
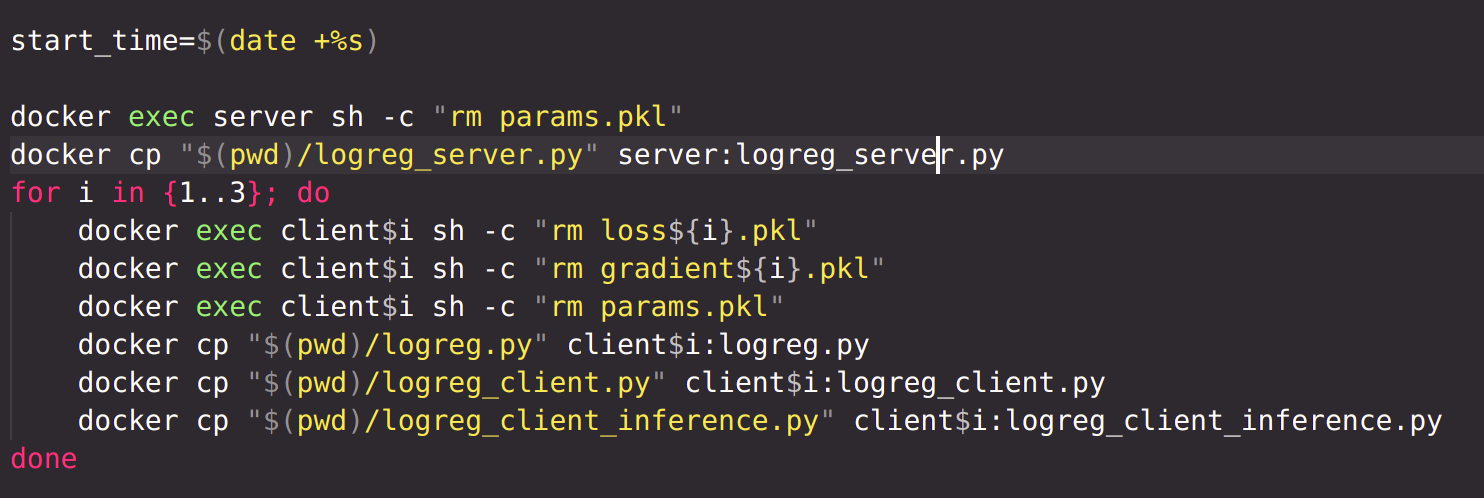For a certain number of epochs, run logreg_client.py which loads previously saved model, runs it for one epoch, saves loss and gradient into files, saves the model. Then, the loss and gradient files are sent to server using netcat. Until they reach the server, the file is resent over and over.
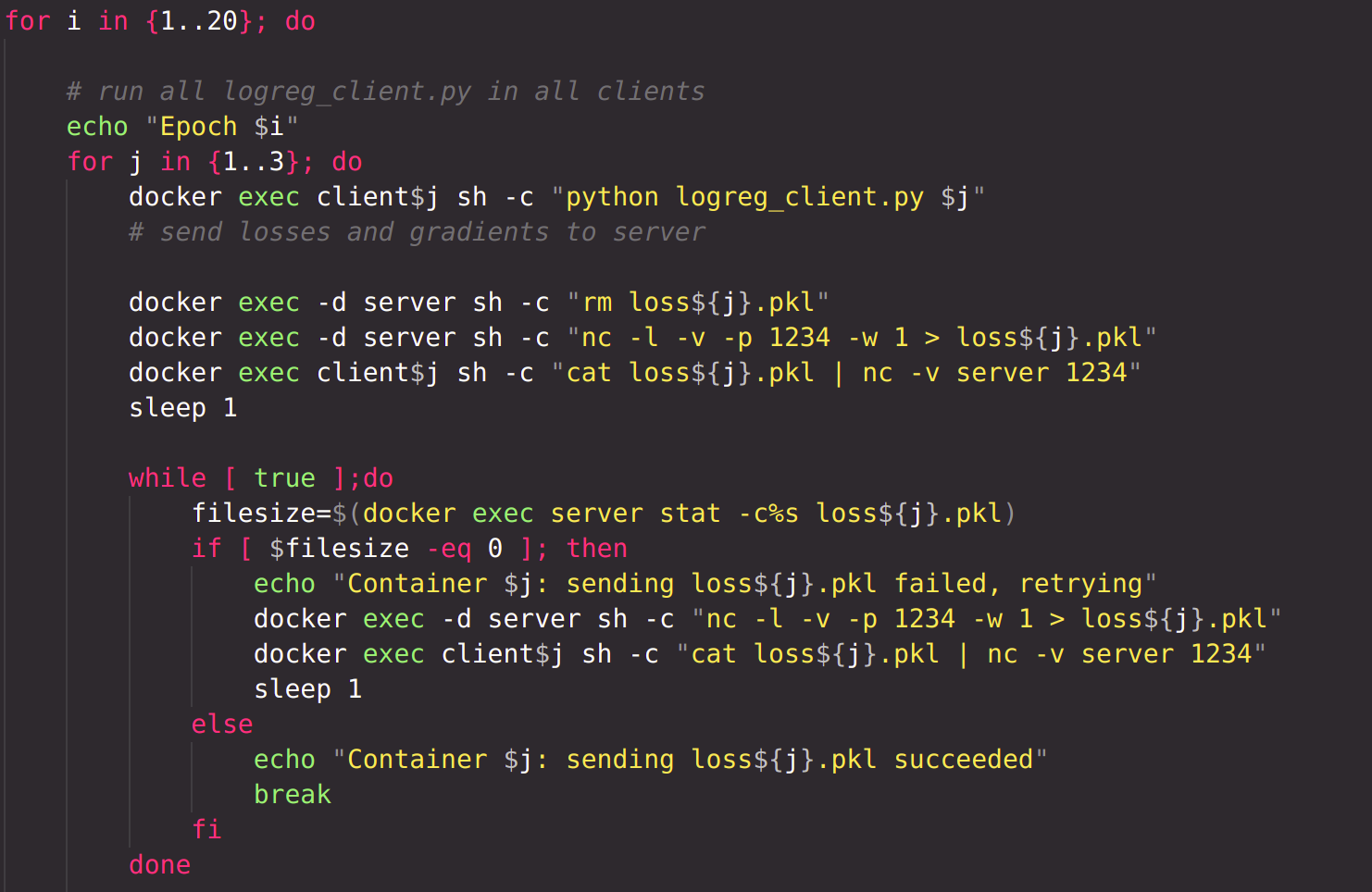
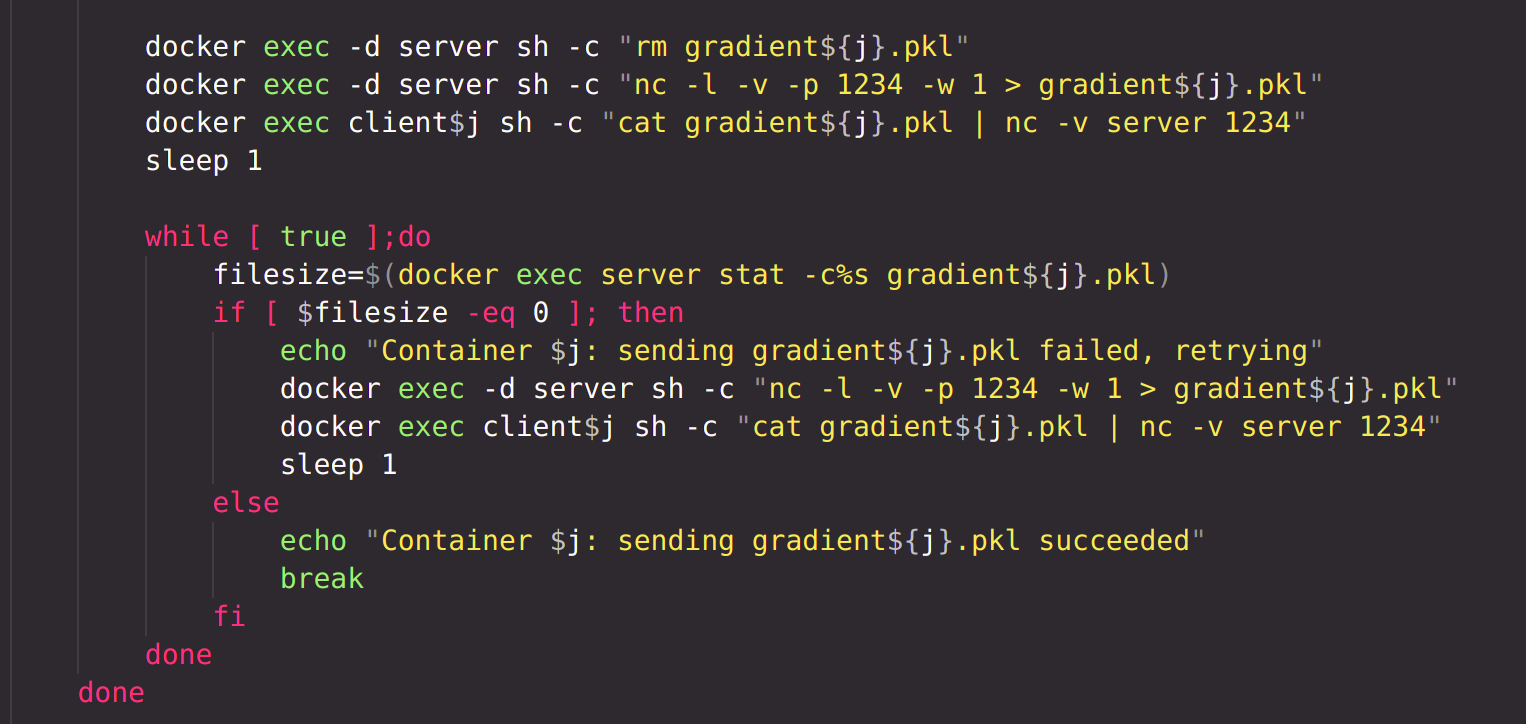
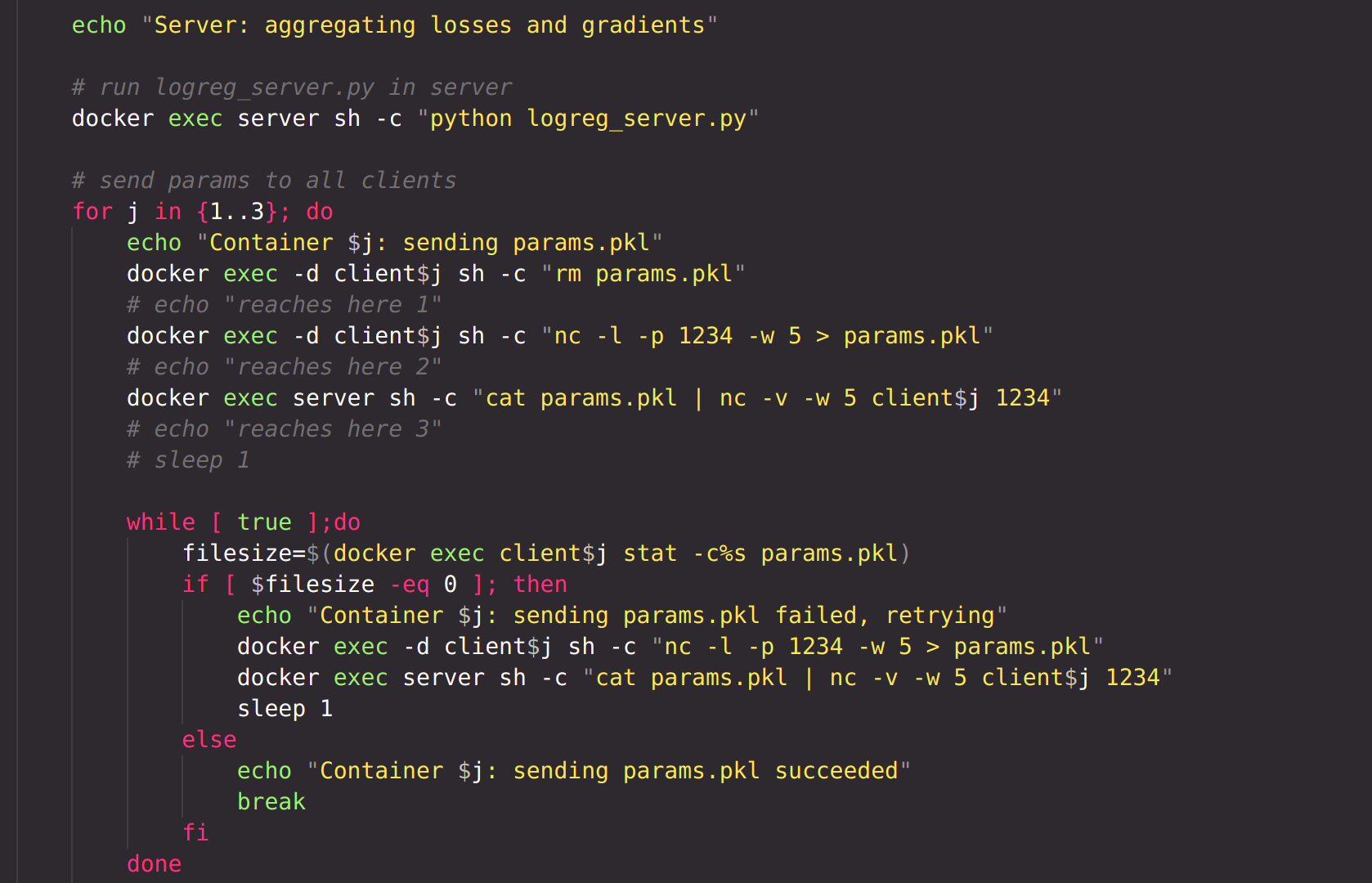
In the server, logreg_server.py is run, which aggregates all the losses and gradients received from each client, generates weights of the model, stores them in file 'params.pkl'. The file is then sent to all clients.
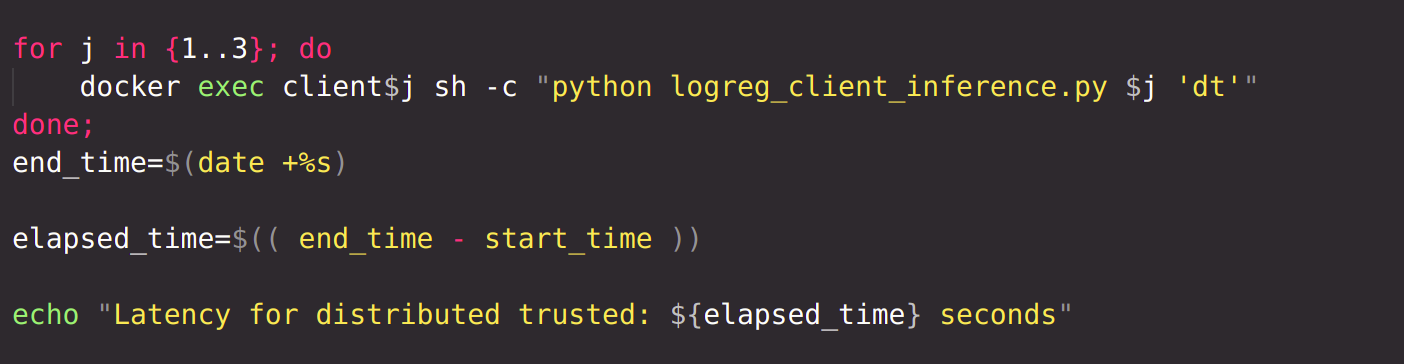
Finally, after the model has been trained for specified epochs, the logreg_client_inference.py file is run on each client locally. Prediction on the test set is generated in each client, and metrics are calculated.
|-----logreg.py
|-----logreg_client.py
|-----logreg_server.py
|-----logreg_client_inference.py
|-----run.sh
- |-----encryption.sh
- |-----phase_2.py
- |-----rsa.py
- |-----decryption.sh
- |-----phase_3.py
- |-----phase_4.py
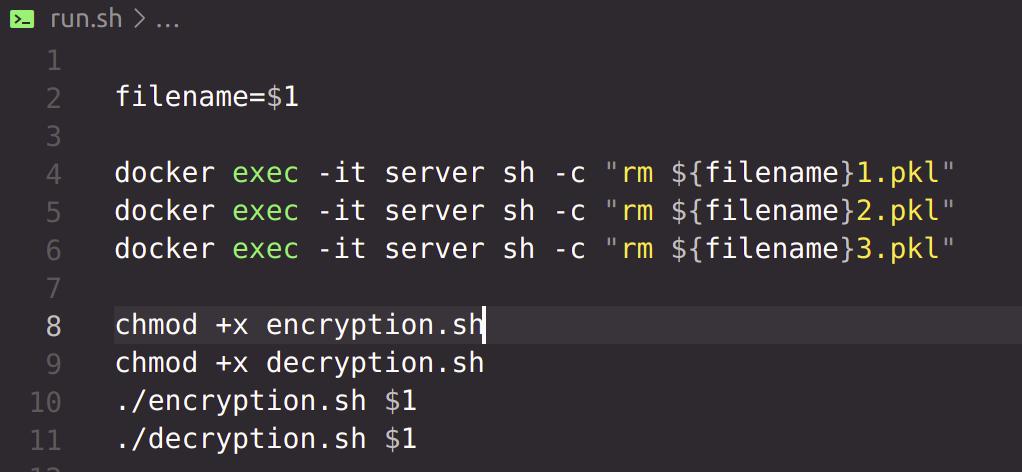
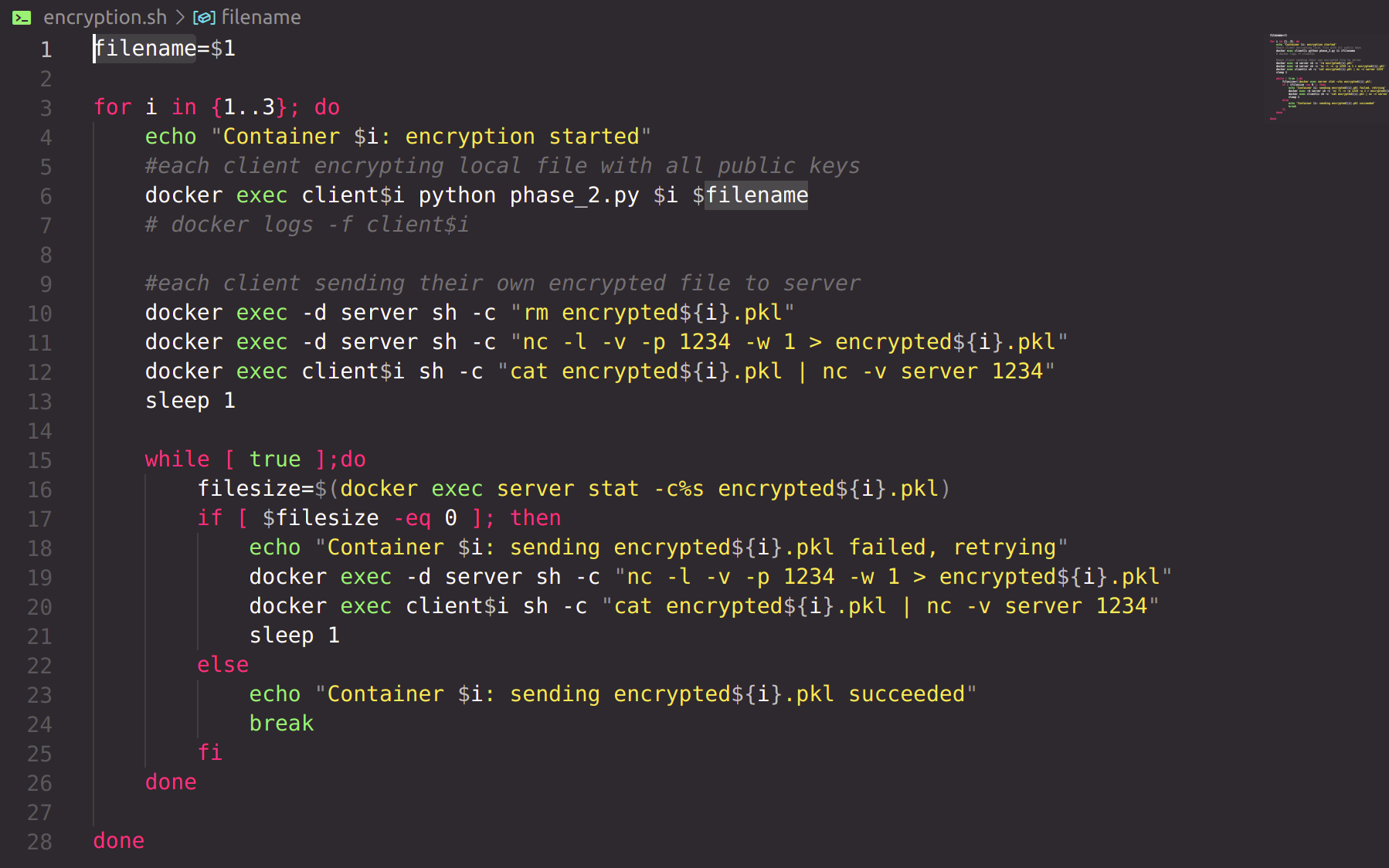
The distributed untrusted scenario is similar to the trusted scenario, except now the losses and gradients are sent from each client to the server following the secure sum protocol. The secure sum protocol is implemented in the run.sh script. The name of the file that has to be sent is provided as a command line argument to this script.
distributed-untrusted.sh
run.sh
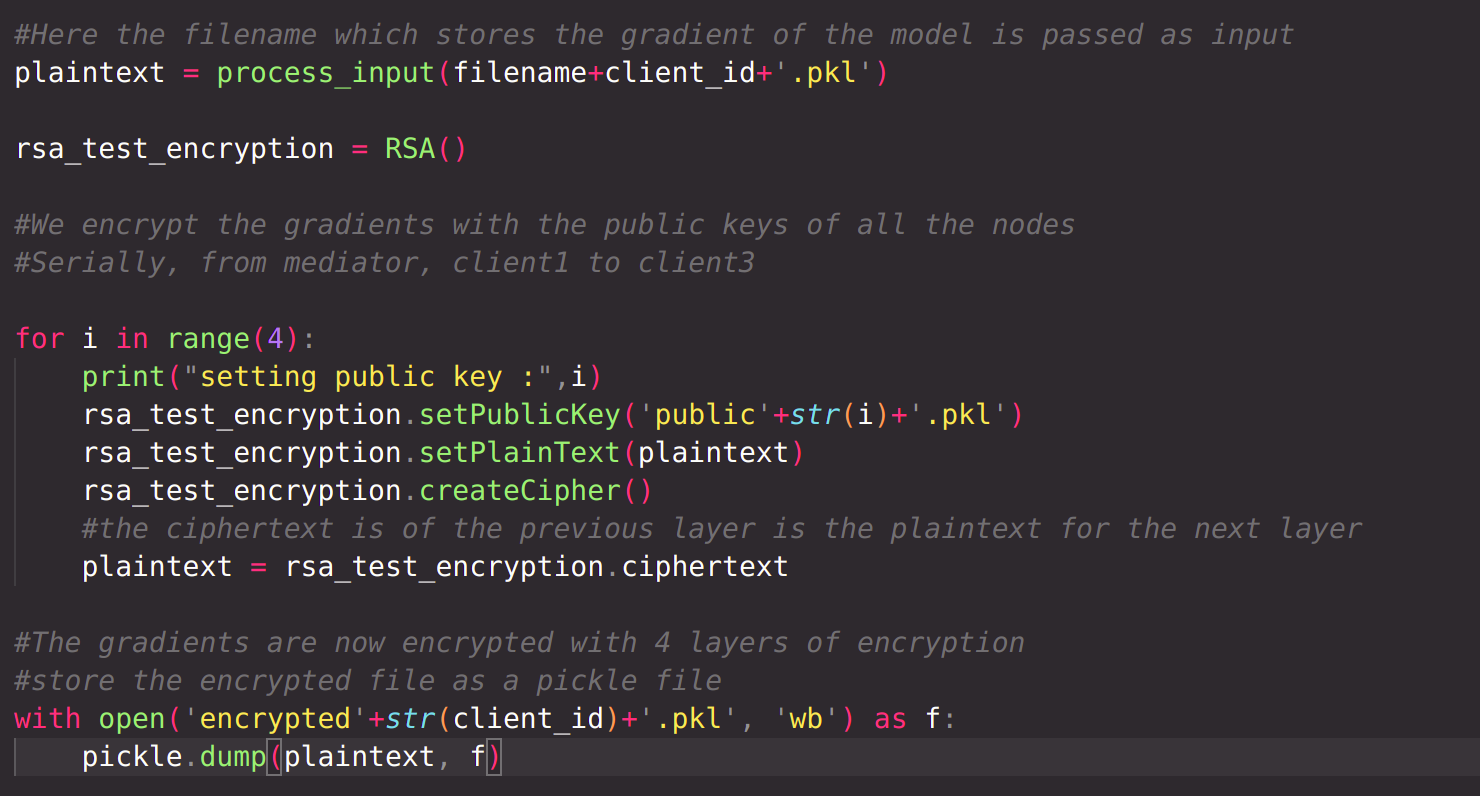
Each client encrypting local file respectively with public keys of client1, client2, client3 and server. Now the local file has 4 layers of encryption. Each encrypted local file is then sent to server.
encryption.sh
The process of multiple-layer encryption with RSA cryptosystem is implemented in the phase_2.py script.
phase_2.py
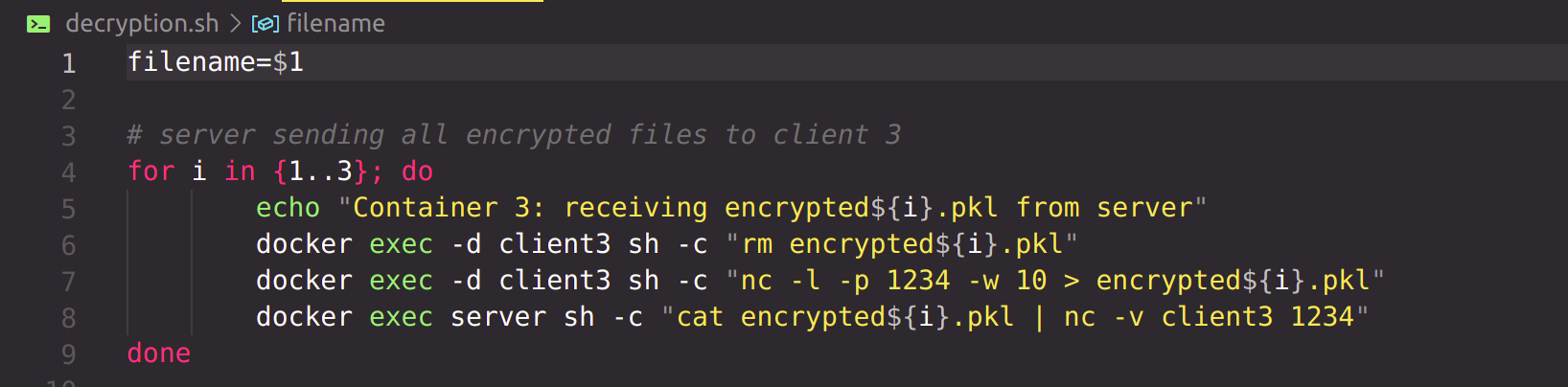
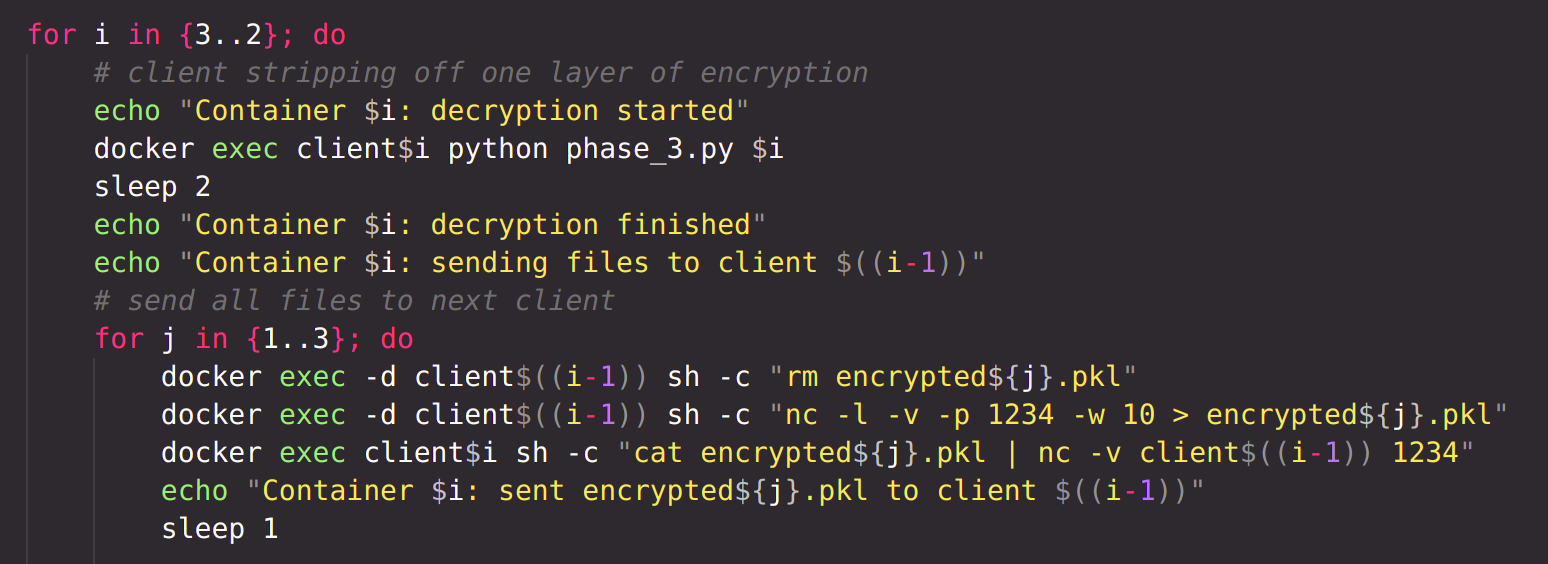
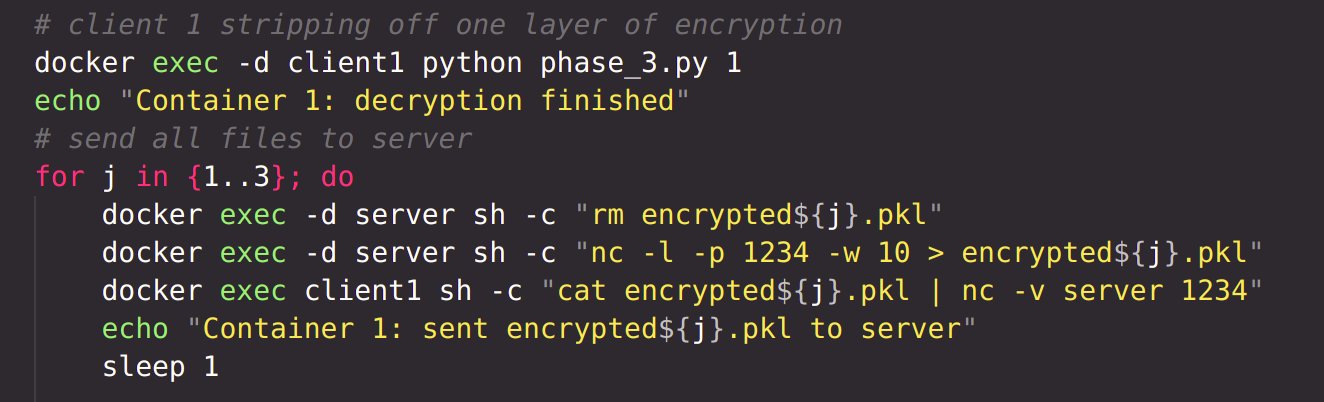
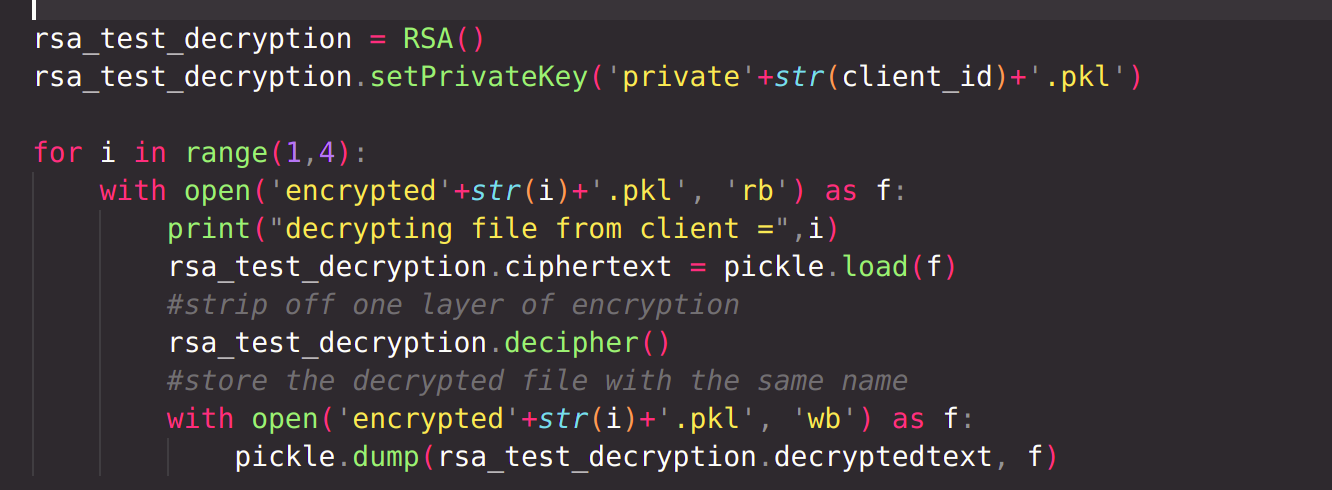
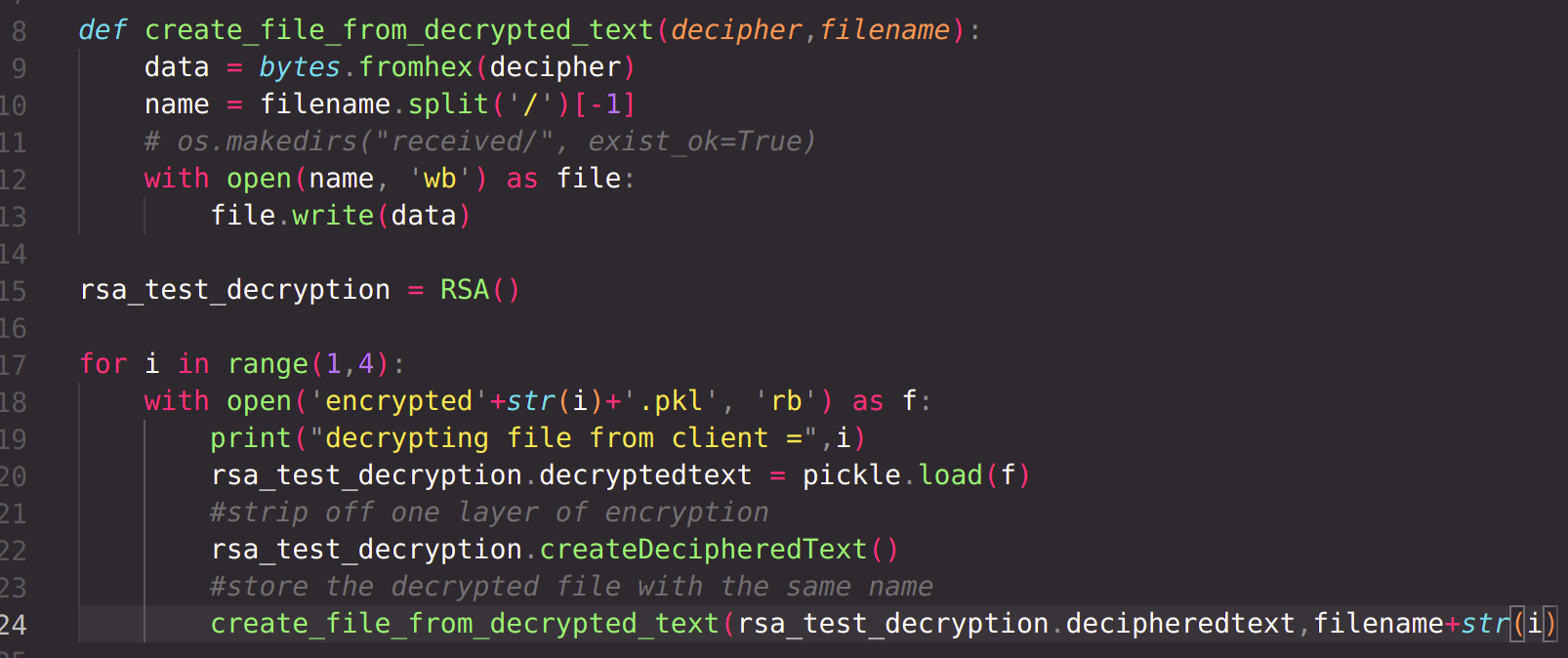
All encrypted files are now at the server. According to the protocol, the server will now send all the encrypted files to Party n. Party n will decrypt all files with it's own private key, stripping off one layer of encryption from all files. Then Party n will send all files to Party n-1, which will perform the same operations. Finally, Party 1 will send the files to server, which will decrypt all files with own private key and reconstruct the files.
decryption.sh
decryption.sh
decryption.sh
decryption.sh
stripping off one layer of encryption from all files :
phase_3.py
reconstruct the files :
phase_4.py
Dataset For Classification: SUSY Dataset
A classification dataset to distinguish between a signal process which produces supersymmetric particles and a background process which does not.
Train set : 10000 Test set : 2000
Dataset For Regression: Bike Sharing Dataset
This dataset contains the hourly and daily count of rental bikes between years 2011 and 2012 in Capital bikeshare system with the corresponding weather and seasonal information.
Centralized Trusted with 10 epochs -
- Accuracy 0.6335
- Recall score 0.7117711771177118
- Precision score 0.5787119856887298
- Latency on centralized trusted: 0.20304107666015625
Distributed Trusted with 10 epochs -
- Accuracy : 0.636
- Precision : 0.8428571428571429
- Recall : 0.12981298129812982
- Latency for distributed trusted: 361 seconds
Distributed Untrusted with 10 epochs -
- Accuracy : 0.636
- Precision : 0.844106463878327
- Recall : 0.24422442244224424
- Latency for distributed untrusted: 3174 seconds
Centralized Trusted with 10 epochs -
- Accuracy 0.4545
- Recall score 1.0
- Precision score 0.4545
- Latency on centralized trusted: 1.637641429901123
Distributed Trusted with 10 epochs -
- Accuracy : 0.4545
- Precision : 0.4545
- Recall : 1.0
- Latency for distributed trusted: 593 seconds
Distributed Untrusted with 10 epochs -
- Accuracy : 0.4545
- Precision : 0.4545
- Recall : 1.0
- Latency for distributed untrusted: 4833 seconds
Centralized Trusted with 10 epochs -
- R2: 0.6006615916518654
- MSE: 0.02731315070372643
- MAE: 0.13545571389229752
- RMSE: 0.165266907467062
- Latency on centralized trusted: 0.06763219833374023
Distributed Trusted with 10 epochs -
- R2: 0.5996337293159302
- MSE: 0.02738345237843939
- MAE: 0.13640264196804466
- RMSE: 0.16547946210463518
- Latency for distributed trusted: 601 seconds
Distributed Untrusted with 10 epochs -
- R2: 0.5996337293159302
- MSE: 0.02738345237843939
- MAE: 0.13640264196804466
- RMSE: 0.16547946210463518
- Latency for distributed untrusted: 4828 seconds