常用数据结构相关的算法,主要是数组、链表相关的算法,比如 双指针算法, 滑动窗口算法 等,不需要什么前置知识,技巧虽然精妙,但你理解起来也不会很困难。但稍微进阶一些的算法技巧,主要是递归相关的算法,比如 回溯算法, 动态规划,或者高级数据结构相关算法 Dijkstra 算法, 字典树算法 等,你不要上来就学它们,否则很容易劝退。这些递归算法需要二叉树算法作为铺垫,你应该先学习我的二叉树专题文章,再去学习这些高级算法,就能融会贯通了。
从 整体到细节,自顶向下 ,从抽象到具体的框架思维是通用的,不只是学习数据结构和算法,学习其他任何知识都是高效的
数据结构的存储方式只有两种: 数组 (顺序存储)和 链表 (链式存储)。
- 先学习像数组、链表这种基本数据结构的常用算法
- 学会基础算法之后,应该先刷二叉树,先刷二叉树,先刷二叉树,最容易培养框架思维的,而且大部分算法技巧,本质上都是树的遍历问题
算法的本质就是「穷举」;能够站在计算机的视角,抽象、化简实际问题,然后用编程的方式去解决问题
- 如何穷举?即无遗漏地穷举所有可能解。
- 如何聪明地穷举?即避免所有冗余的计算,消耗尽可能少的资源求出答案。
- 在做题的时候要思考,联想,进而培养举⼀反三的能力
数组链表代表着计算机最基本的两种存储形式:顺序存储和链式存储,所以他俩可以算是最基本的数据结构;
前缀和技巧适用于 快速、频繁地计算⼀个索引区间内的元素之和 。前缀和的核心内容就是新建一个数组,数组内的元素 preNum[i] 为原数组 [0…i] 的和;
class PrefixSum {
// 前缀和数组
private int[] prefix;
/* 输入一个数组,构造前缀和 */
public PrefixSum(int[] nums) {
prefix = new int[nums.length + 1];
// 计算 nums 的累加和
for (int i = 1; i < prefix.length; i++) {
prefix[i] = prefix[i - 1] + nums[i - 1];
}
}
/* 查询闭区间 [i, j] 的累加和 */
public int query(int i, int j) {
return prefix[j + 1] - prefix[i];
}
}303. Range Sum Query - Immutable Org Doc
这个技巧在生活中运用也挺广泛的,比方说,你们班上有若干同学,每个同学有⼀个期末考试的成绩(满 100 分),那么请你实现⼀个 API,输⼊任意⼀个分数段,返回有多少同学的成绩在这个分数段内。
304. Range Sum Query 2D - Immutable
- 差分数组和前缀和比较类似,不一样的是,差分数组适合频繁对原始数组的某个区间的元素进行增减。
- 构造类似前缀和的 prefix 数组,对原始 nums 数组构造一个 diff 数组,diff 数组的内容就是 nums 数组前后元素的差值, diff[i] = nums[i] - nums[i-1];
现在我们把差分数组抽象成⼀个类,包含 increment 方法和 result 方法:
class Difference{
private int[] diff;
// 构造函数,构造 diff 数组
public Difference(int[] nums){
if(nums.length <=0){
return;
}
diff = new int[nums.length+1];
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i-1];
}
}
// 修改 diff 数组
public void increment(int start,int end,int incr){
// 更新 diff 数组, diff[start...end] + incr diff[end...] - incr
for (int i = start; i < end; i++) {
diff[i] += incr;
}
for (int j = end; j < diff.length; j++) {
diff[j] -= incr;
}
}
// 根据 diff 和原始的 nums 数组,计算结果
public int[] result(){
int[] res = new int[diff.length];
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = diff[i] + res[i-1];
}
return res;
}
}1109. Corporate Flight Bookings
还有一个很类似的题目:
26. Remove Duplicates from Sorted Array
167. Two Sum II - Input Array Is Sorted
使用双指针由内向外移动,相当于暴力解决,可以使用动态规化的方式,这个需要等到动态规化的时候再说 TODO: 5. 最长回文子串
对于单链表的题目,双指针的应用还是非常广泛的。。
基本规律:
- 首先使用到了 虚拟头节点 的技巧,也就是里面的 dump 节点
- 其次,使用到了 p 节点,作为 dump 列表上的一个可移到的头节点,就像拉链的拉头;
- 最后,使用两个分别作为 p1,p2 两个节点的可移动的节点,就像拉链两边的锯齿;
- 这里使用了优先级队列的数据结构,将每个链表的头结点都加到最小堆中,就可以每次获得 k 个节点中的最小结点;
- 还有一个方法就是使用二分和递归的方式,两两进行组合,就是跟上面的合并两个有序链表一个思路了,具体实现可以看下面的程序;
怎么判断是否是环形链表?快慢指针,如果相遇,则是环形链表 141. Linked List Cycle 判断环的起点 142. Linked List Cycle II
- 怎么获得倒数第 K 个节点?如果想获得第 K 个节点,可以 for 循环直接遍历;
- 求倒数 K 个节点 -> 那就是求 N - K 位置的节点
- 怎么知道 N 是多少呢?需要循环一次才能知道,那怎么循环一次就能知道 N-K 呢?
- 设置快慢指针,快指针到 K 的时候,慢指针从 Head 节点出发,两个指针同速前进,快指针到末尾,慢指针的位置就是 N-K 了
ListNode findFromEnd(ListNode head, int k) {
ListNode fast = head;
ListNode slow = head;
int point = 0;
while (fast != null) {
point += 1;
fast = fast.next;
if (point >= k) {
slow = solw.next;
}
}
return solw;
}19. Remove Nth Node From End of List
通过快慢指针来避免第一次获取长度 N,第二次循环到 N/2 的问题,可以一次循环解决问题 876. Middle of the Linked List
因为两个链表的长度不一致,导致使用双指针的时候不知道两个指针什么时候出发合适; HeadA 路程是 a -> c -> b 总数是 A HeadB 路程是 x -> c -> b 总数是 B 可以让 point1 先从 HeadA 出发,走完 HeadA 之后,从 HeadB 出发,此时已经走了路程 A 让 pint2 从 HeadB 出发,走完 HeadB 之后,从 HeadA 出发,此时已经走了路程 B Point1 - Point2 = a - x; 因此: Point1 + x = Point2 + a 从而可以看到,两个再分别通过均速走就可以在交点相遇
160. Intersection of Two Linked Lists ****
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
unordered_map<char, int> need, window;
# 将字符map 到数组中,数组的含义就是字符出现的次数
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}76. 最小覆盖子串
一个根据套路完成的。。成了默写了哈哈 567. 字符串的排列
这个有问题,需要后面再看下 438. 找到字符串中所有字母异位词
3. 无重复字符的最长子串
int binarySearch(int[] nums, int target) {
int left = 0, right = ...;
while(...) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
...
} else if (nums[mid] < target) {
left = ...
} else if (nums[mid] > target) {
right = ...
}
}
return ...;
}704. 二分查找
- 二叉树的思维方式: a. 从上自下的进行遍历 b. 从下自上的递归
- TODO 哪些问题可以用二叉树的思维解决?
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 前序位置
traverse(root.left);
// 中序位置
traverse(root.right);
// 后序位置
}A 在递归调用链表的时候,如何去用递归的方式完成?
/* 递归遍历单链表 */
void traverse(ListNode head) {
if (head == null) {
return;
}
// 前序位置
traverse(head.next);
// 后序位置
}可以看到,实际上对树的遍历就是对链表遍历的扩展,所谓的前序和后序只不过是在递归调用的不同的位置,后序主要就是利用了调用的堆栈,实现了倒序弹出
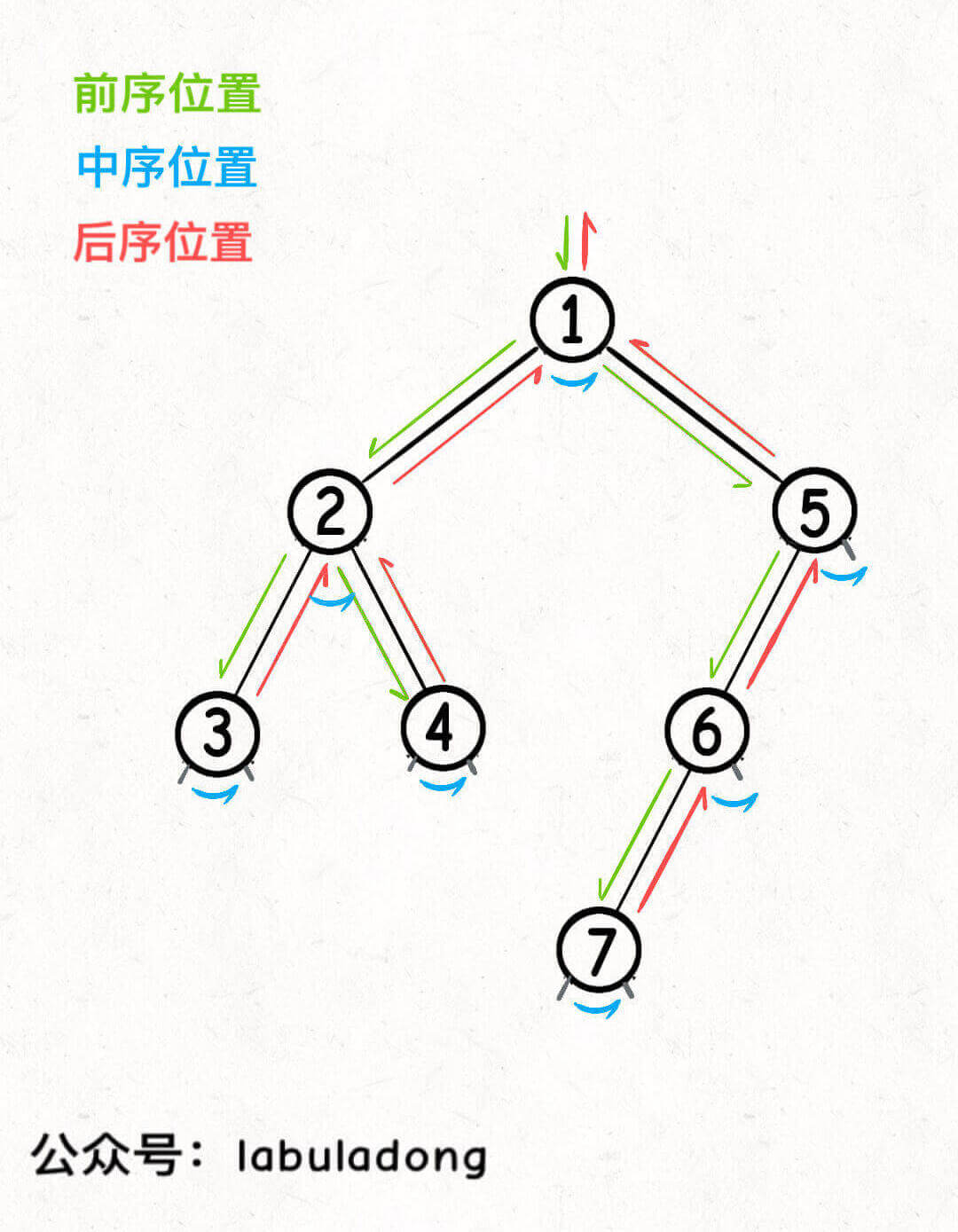
要记住这个图:
前中后序是遍历二叉树过程中处理每一个节点的三个特殊 时间点 ;二叉树的所有问题,就是让你在前中后序位置注入巧妙的代码逻辑,去达到自己的目的,你只需要单独思考 每一个节点应该做什么 ,其他的不用你管,抛给二叉树遍历框架,递归会在所有节点上做相同的操作。
综上,遇到一道二叉树的题目时的通用思考过程是:
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值。
3、无论使用哪一种思维模式,你都要明白二叉树的每一个节点需要做什么,需要在什么时候(前中后序)做。
- 可以利用后序遍历将层数+1,取 Max 值如这个题:No104 树的最大深度
- 后序遍历计算最大值,为啥是后序遍历?-> No543 二叉树的直经
- 将二叉树展开为链表 114. 二叉树展开为链表[fn:3] 大致思路可以整理为节点的左侧节点,拼接到 root 的右节点上,原本的右节点拼接到原左节点的下面;从子节点向根节点分析,那需要是后序遍历,先遍历到子节点,然后拆分子节点,从而构造根节点。
- 一旦你发现题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置写代码了 ->652. 寻找重复的子树 [fn:4] 这里的大致思路就是需要从下至上看子树是否和其他子树一致,如果一致,则向上遍历再比较
- 看当前值是否 <min 或者 >max, 确定是否要裁剪还是继续向下遍历 -> No669 树的裁剪 如何做裁剪?裁剪无非就是把当前节点这只为 null 说明这个接口以及后面的节点都被裁减掉了
- 实战 1:simple 226. 翻转二叉树 [fn:1]
当遇到将树按照层的维度连接或查询,实际就是树的广度优先算法,比如这道题 : 116. 填充每个节点的下一个右侧节点指针[fn:2] 这道题实际上有两种解决方式
- 一种是上面的解决方式,利用栈的特性,将每层数据先放到栈中,再依次弹出栈元素,关键在于如何处置层与层之间的关系,这里使用的是固定推到栈中的一层数据的 size,下次只弹出 size 个元素,这些元素就是在一层内的所有元素;
- 另一种是二叉树的相邻节点抽象成一个「三叉树节点」,这样二叉树就变成了一棵「三叉树」,然后你去遍历这棵三叉树,把每个「三叉树节点」中的两个节点连接就行了: 116. 填充每个节点的下一个右侧节点指针
[fn:4] https://leetcode.cn/problems/find-duplicate-subtrees/
[fn:3] https://leetcode.cn/problems/flatten-binary-tree-to-linked-list/ [fn:2] https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/ [fn:1] https://leetcode.cn/problems/invert-binary-tree/