SIR-Hawkes: Linking Epidemic Models and Hawkes Processes to Model Diffusions in Finite Populations

This repository contains:

Scripts for SIR-Hawkes project: simulation, modeling with SIR and HawkesN.
Three datasets consist of tweet cascades.
A hands-on tutorial to walk you through some main components of the project: simulation, modeling and population size distribution.

Citation

The project was introduced in this paper:

Marian-Andrei Rizoiu, Swapnil Mishra, Quyu Kong, Mark Carman, Lexing Xie. 2018. SIR-Hawkes: 
Linking Epidemic Models and Hawkes Processes to Model Diffusions in Finite Populations. . 
In WWW 2018: The 2018 Web Conference, April 23–27, 2018, Lyon, France. ACM, New York, NY, 
USA, 10 pages. https://doi.org/10.1145/3178876.3186108

License

Both dataset and code are distributed under the Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0) license, a copy of which can be obtained following this link. If you require a different license, please contact us at Marian-Andrei@rizoiu.eu or Lexing.Xie@anu.edu.au.

SIR-Hawkes tutorial

required packages:

- nloptr
- parallel
- data.table

1. Preliminary

We need to first load all required packages for simulation and modeling cascades.

library(parallel)
source('scripts/functions-SIR-HawkesN.R')
source('scripts/functions-size-distribution.R')

2. Stochastic R simulation

We then simulate 20 stochastic SIR realizations. In this step, we chose a set of parameters ( $N = 1300, I_0 = 300, \gamma = 0.2, \beta = 1$ ) for simulation. Given those simulated events, we are going to fit them with both SIR model and our proposed HawkesN model to see their modeling performance.

params.S <- c(N = 1300, I.0 = 300, gamma = 0.2, beta = 1)
nsim <- 20
simdat <- replicate(
    n = nsim,
    generate.stochastic.sir(params = params.S, Tmax = 11, hide.output = T)    
)

Let's take a look at the simulated data (only the first 20 events of the first simulation were shown).

One simulation is identified as four components: - relative times - susceptible population size at each time - infected population size at each time - recovered population size at each time

as.data.frame(simdat[,1])[1:20,]

time	S	I	R	C
0.000000000	1000	300	0	300
0.001861149	999	301	0	301
0.002054043	998	302	0	302
0.002297054	997	303	0	303
0.003679539	996	304	0	304
0.005308822	995	305	0	305
0.010011856	995	304	1	305
0.013833165	995	303	2	305
0.015425608	994	304	2	306
0.018386120	993	305	2	307
0.018890458	992	306	2	308
0.019177649	992	305	3	308
0.032191757	991	306	3	309
0.035561494	990	307	3	310
0.037340979	989	308	3	311
0.038834789	988	309	3	312
0.041421224	987	310	3	313
0.041912680	986	311	3	314
0.043324751	985	312	3	315
0.051393662	984	313	3	316

3. Fit Stochastic SIR on simulated cascades

We fit stochastic SIR in the following steps:

Choose a starting point for all parameters.
Apply LBFGS algorithm for optimizing the likelihood function of SIR model (This step might take quite a lot of time).

# initial fitting point for each execution
params.fit.start <- c(N = 0.1, I.0 = 0.1, gamma = 0.1, beta = 0.1)

.cl <- makeCluster(spec = min(nsim, detectCores()), type = 'FORK')
results <- parSapply(cl = .cl, X = 1:nsim, FUN = function(i) {
    mysim <- as.data.frame(simdat[, i])
    return(fit.stochastic.sir(mysim, params.fit.start))
})
stopCluster(.cl)

# reconstruct result data format
res <- as.data.frame(results[1,])
names(res) <- 1:nsim             
res <- as.data.frame(t(res))     
res$ll <- unlist(results[2,])
complete_res <- res

In the following block, we show how well parameters were retreived by our fitting process. Generally, the median values are closed to the theoretical values with a small standard deviation.

# let's see how well parameters were retreived
prnt <- rbind(params.S[c('N', 'I.0', 'gamma', 'beta')], 
              apply(X = complete_res[, c('N', 'I.0', 'gamma', 'beta')], MARGIN = 2, FUN = median),
              apply(X = complete_res[, c('N', 'I.0', 'gamma', 'beta')], MARGIN = 2, FUN = sd))
rownames(prnt) <- c('theoretical', 'median', 'sd')
print(prnt[, c('N', 'I.0', 'gamma', 'beta')], digits = 2)

                 N I.0 gamma  beta
theoretical 1300.0 300 0.200 1.000
median      1283.5 300 0.200 0.986
sd             3.6   0 0.006 0.026

4. Fit HawkesN on simulated cascades

We need first to pull out the infective events for HawkesN model.

# get the means at given time points, to be able to compare to deterministic
simhistory <- sapply(X = 1:nsim, FUN = function(i) {
  history.S <- SIR2HAWKES.stochastic.event.series(state = simdat[,i])  
})

We model HawkesN on the simulated data following same steps as modeling SIR:

Choose a starting point for all parameters.
Apply LBFGS algorithm for optimizing the likelihood function of HawkesN model (this step might take quite a lot of time).

# start point 
params.fit.start <- c(K = 1, c = 0.1, theta = 0.1, N = 1000)

# fit the event series with HawkesN
.cl <- makeCluster(spec = min(20, detectCores()), type = 'FORK')
results <- parSapply(cl = .cl, X = 1:nsim, FUN = function(i) {
  history.S <- as.data.frame(simhistory[,i])
  fitted.model <- fitSeries(history = history.S, params.fit.start)
})
stopCluster(.cl)
res <- as.data.frame(results['par',])
names(res) <- 1:nsim
res <- data.frame(t(res))

We compare the fitted HawkesN parameters with theoretical HawkesN parameters.

# these are the theoretical parameters
params.H <- c(K = 5, c = 0.001, theta = 0.2, N = 1300)

prnt <- rbind(params.H, 
              apply(X = res, MARGIN = 2, FUN = median, na.rm = T),
              apply(X = res, MARGIN = 2, FUN = sd, na.rm = T))
rownames(prnt) <- c('theoretical', 'median', 'sd')
print(prnt[, c('K', 'theta', 'c', 'N')], digits = 2)

              K theta     c    N
theoretical 5.0  0.20 0.001 1300
median      5.5  0.18 0.100 1292
sd          2.1  8.52 0.000   11

We then compare the fitted HawkesN parameters with theoretical SIR parameters. Theorem 3.1 in our paper reveals the link between HawkesN and SIR models that:

Suppose the new infections in a stochastic SIR process of parameters ${\beta, \gamma, N}$ follow a point process of intensity $\lambda^I(t)$ . Suppose also the events in a HawkesN process with parameters ${\mu, \kappa, \theta, N}$ have the intensity $\lambda^H(t)$ . Let $\mathcal{T} = {\tau_1, \tau_2, \ldots}$ be the set of the times to recovery of the infected individuals in SIR. The expectation of $\lambda^I(t)$ over $\mathcal{T}$ is equal $\lambda^H(t)$ : $E_\mathcal{T}[ \lambda^I(t)] = \lambda^H(t)$ , when $\mu = 0$ , $\beta = \kappa \theta$ , $\gamma = \theta$ .

Given this theorem, we are able to convert HawkesN parameters into SIR parameters and compare them with theoretical SIR parameters.

res$gamma <- res$theta
res$beta <- res$K * res$theta
prnt <- rbind(params.S[c('N', 'gamma', 'beta')], 
              apply(X = res[, c('N', 'gamma', 'beta')], MARGIN = 2, FUN = mean, na.rm = T),
              apply(X = res[, c('N', 'gamma', 'beta')], MARGIN = 2, FUN = sd, na.rm = T))
rownames(prnt) <- c('theoretical', 'median', 'sd')
print(prnt[, c('N', 'gamma', 'beta')], digits = 2)

               N gamma beta
theoretical 1300   0.2  1.0
median      1295   3.5  6.4
sd            11   8.5 13.7

5. Plotting size distribution

In this section, we will study the probability distribution of population size for a given set of parameters.

# theoretical parameters shown previously
params.S <- c(N = 1300, I.0 = 300, gamma = 0.2, beta = 1)
params.H <- c(K = 5, c = 0.001, theta = 0.2, N = 1300)

Let's calculate the transition matrix and the states mapping matrix for an SIR model with the given parameters.

.transition <- construct.transition.matrix.and.states(params = params.S)

Then we construct the event history in required format for HawkesN and we choose the first cascade from our simulated data.

seen_perc <- 0.5
history <- as.data.frame(simhistory[,1])
seenEvents <- round(nrow(history) * seen_perc)

Then we get two size distributions for two scenarios:

when only 1 event is observed (apriori probability size distribution)
when half of events are observed (aposteriori probability size distribution)

# compute size probs at event 1 and current event
size.est.at.zero <- get.size.distribution(params = params.H, .transition = .transition)
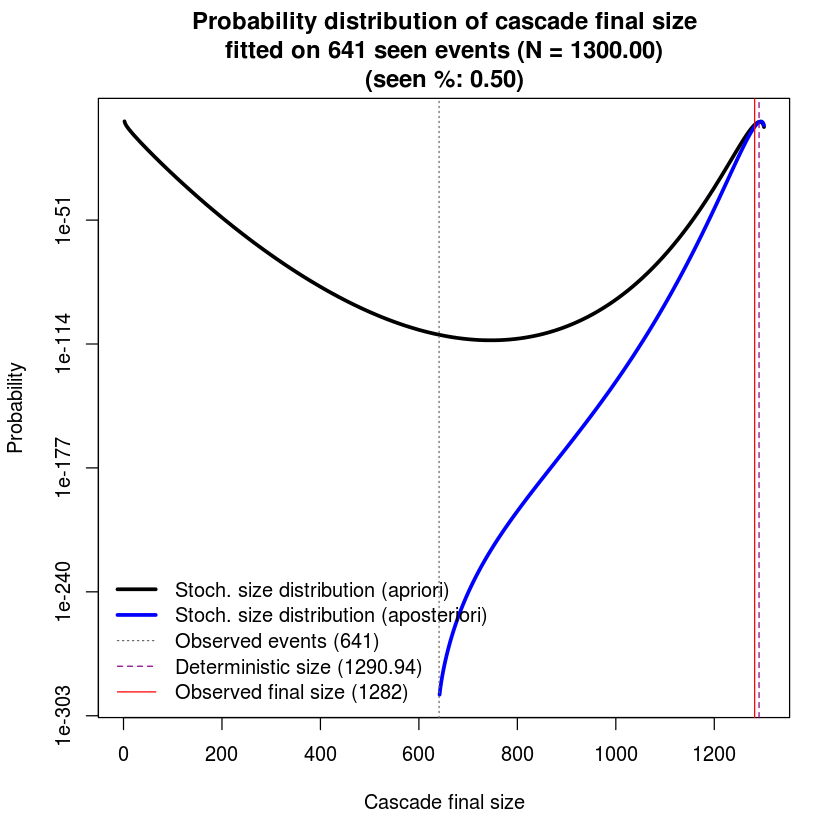
size.est.at.end <- get.size.distribution(params = params.H, .transition = .transition, history = history[seq(seenEvents),])

We then plot both apriori probability size distribution and aposteriori probability size distribution.

# plot our cascade
matplot(cbind(size.est.at.zero$final.state, size.est.at.end$final.state), 
        col = c('black', 'blue'), type = 'l', log = 'y', lty = c(1, 1), lwd = 3,
        xlab = 'Cascade final size', ylab = 'Probability',
        main = sprintf('Probability distribution of cascade final size\nfitted on %d seen events (N = %.2f)\n(seen %%: %.2f)', 
                       seenEvents, params.H['N'], seen_perc) )
abline(v = seenEvents, lty = 3, col = 'gray40')
abline(v = size.est.at.end$theo.mean, lty = 2, col = 'darkmagenta')
abline(v = nrow(history), lty = 1, col = 'red')
legend('bottomleft', 
        legend = c('Stoch. size distribution (apriori)', 
                   'Stoch. size distribution (aposteriori)',
                   sprintf('Observed events (%d)', seenEvents), 
                   sprintf('Deterministic size (%.2f)', size.est.at.zero$theo.mean), 
                   sprintf('Observed final size (%d)', nrow(history)) ), 
        lty = c(1, 1, 3, 2, 1), lwd = c(3, 3, 1, 1, 1), col = c('black', 'blue', 'gray40', 'darkmagenta', 'red'), bty = 'n')

Warning message in xy.coords(x, y, xlabel, ylabel, log = log):
“642 y values <= 0 omitted from logarithmic plot”Warning message in xy.coords(x, y, xlabel, ylabel, log):
“1 y value <= 0 omitted from logarithmic plot”

Several observations (Sec 6.3 in our paper):

The apriori probability size distribution shows two maxima. This provides the following explanation for the general perceived unpredictability of online popularity. For cascades showing a bi-modal apriori size distribution, there are two likely outcomes: either it dies out early or it reaches a large size compared to the maximum population $N$ . At time $t = 0$ is it impossible to di erentiate between the two outcomes.
The aposteriori probability distribution reflects the information gained from the observed events and it shows a single maximum towards the higher size values. The more events we observe, the higher the likelihood of the true value of cascade size.

Notlaughinggirl/sir-hawkes