/linear-programming-manhattan-distance

This program is an algorithm using linear programming to solve an optimization problem which is to minimize the Manhattan distance of given points.

Primary LanguagePython

Optimization of the positioning of relay points on Manhattan using a linear program

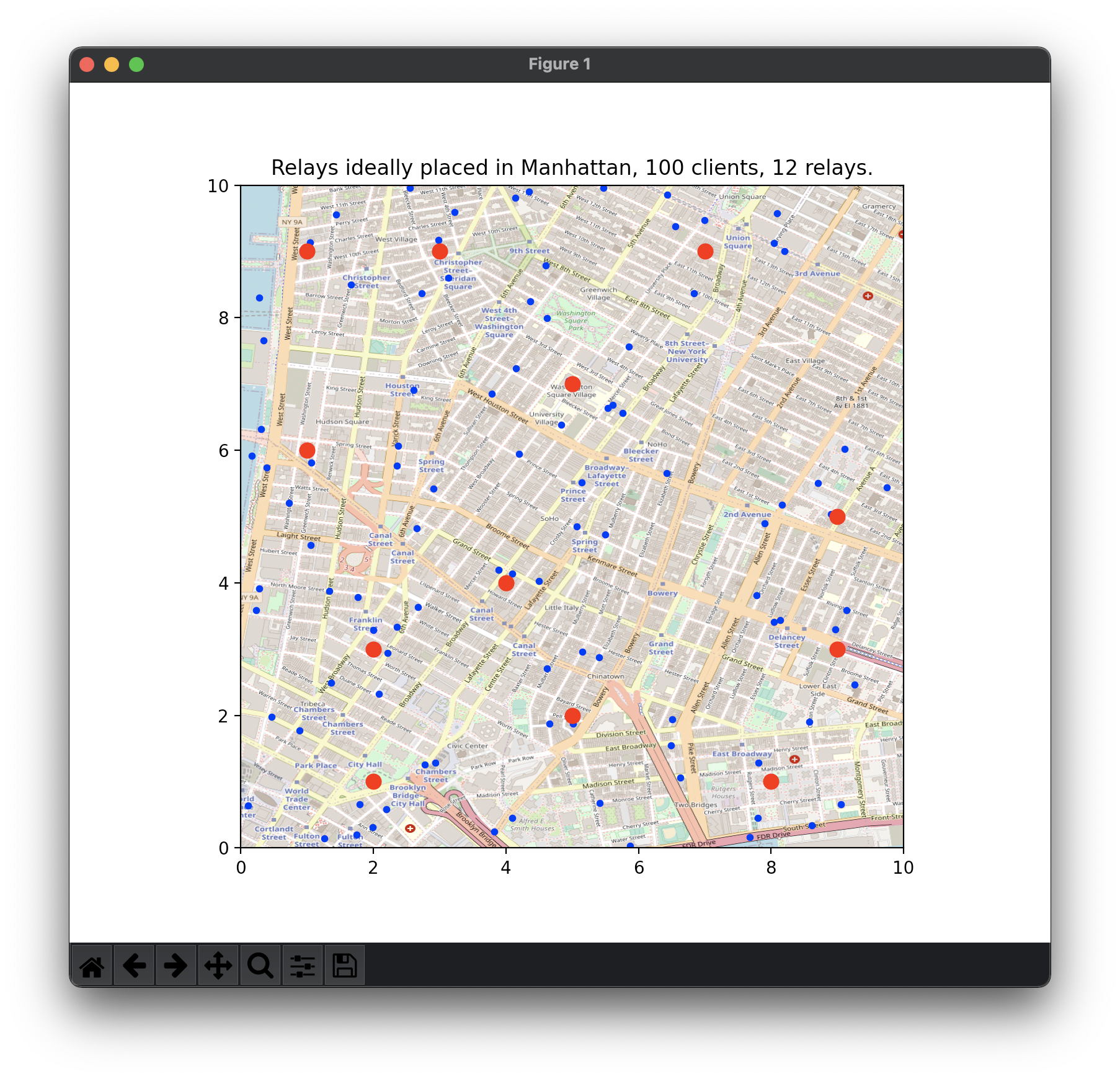
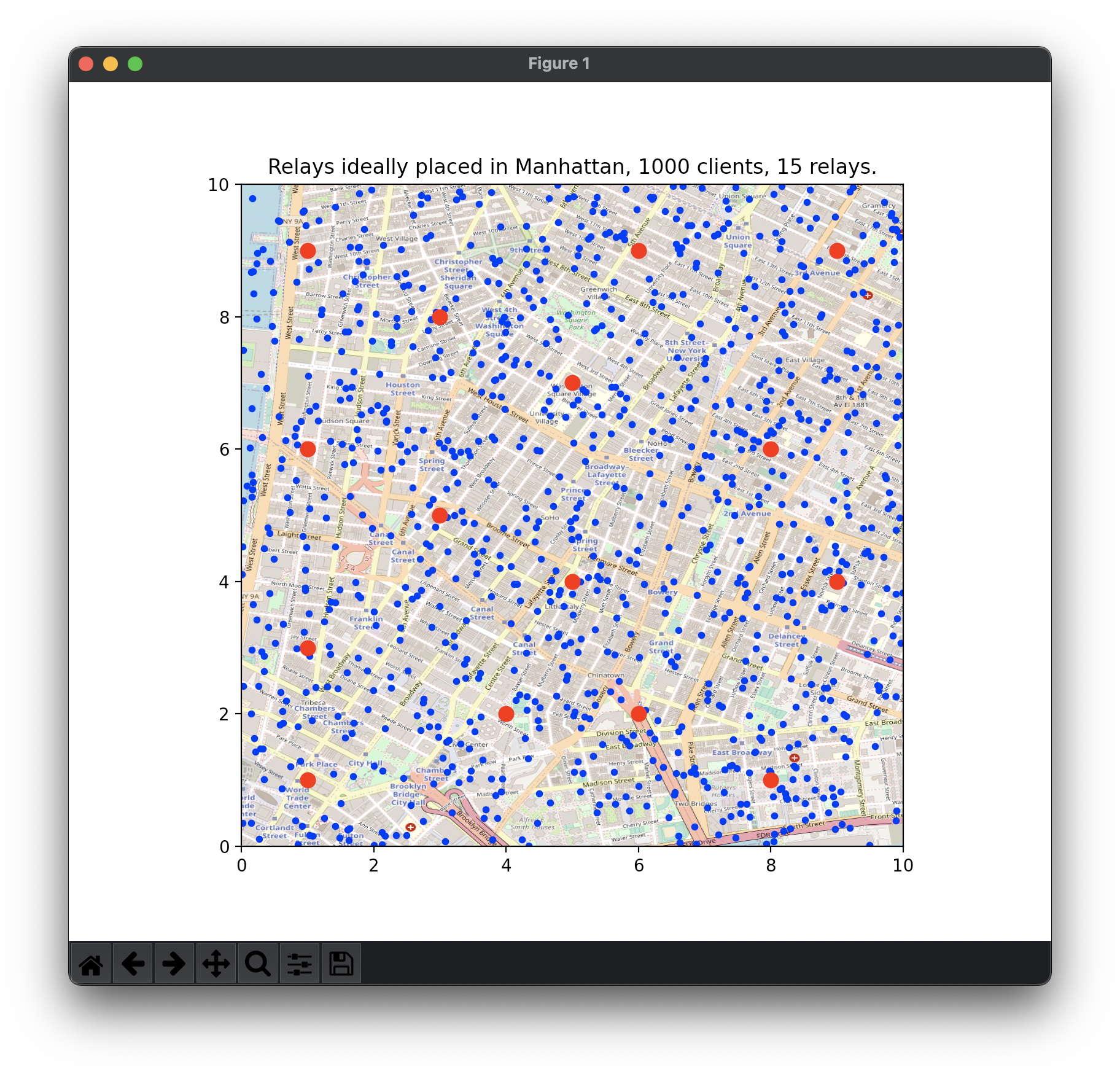
This program is an algorithm using linear programming to solve an optimization problem which is to minimize the Manhattan distance of given points. A clustering method is used to divide the population in several sub-groups on which apply the Simplex algorithm.

Usage

from manhattan import solve

M = [(10, 20), (15, 45), (22, 19), (33, 42)]
p = 2
sol = solve(M, p)

# sol = [(14.0, 19.0), (21.0, 43.0)]

This sample code will basically return the 2 optimized positions for the given set of coordinates M.

Visualization examples

Files

  • linear-programming-manhattan:
    • AUTHORS
    • README
    • manhattan.py: the library, only import solve()
    • manhattan_poc.py: proof of concept using some 2D plot visulization
    • unit_tests.py: unit tests
    • manhattan_city_demo.py: perform the algorithm on Manhattan map
    • SYNTHESE_A.pdf: a brief thesis about the algorithm implementation