get in touch if you'd like to set this up for youself, it's kind of like an LLM for interacting with Harmony, via the Haskell language, TidalCycles, or command line app
The Harmonic Algorithm, written in Haskell and R, generates musical domain specific data inside user defined constraints then filters it down and deterministically ranks it using a tailored Markov Chain model trained on ingested musical data. This presents a unique tool in the hands of the composer or performer which can be used as a writing aid, analysis device, for instrumental study or even in live performance.
This open-source project is based on a long term research agenda that I've pursued for many years, originating from an interest as an electric bass player in performance and composition utilising the overtones of the instrument.
The Harmonic Algorithm takes the underpinning theoretical ideas from this research and realises them in a Command Line Interface. The Harmonic Algorithm is not just useful for electric bass players, but can be utilised by composers and performers on or for any instrument.
The original 2016 research documents on which The Harmonic Algorithm (2018) draws influence can be accessed at the following links:
Core document: original core document (2016)
Reflective document: original reflective document (2016)
The accompanying document for this 2018 project which discusses The Harmonic Algorithm as a creative system can be accessed here: creative system document (2018)
- Haskell Stack Tool (https://docs.haskellstack.org/en/latest/install_and_upgrade/)
- R Interpreter (https://cran.r-project.org/)
- TidyVerse packages for R (from inside R, execute the command
install.packages("tidyverse"))
Once dependencies have been installed, the following steps can be used to build the executable:
- Clone with git (recommended) or download and unzip the Harmonic Algorithm
repository from GitHub. To clone with git, make sure that git is installed on
your system and execute
git clone https://github.com/OscarSouth/theHarmonicAlgorithmin the desired location. - In a terminal or command prompt, navigate to the Harmonic Algorithm directory.
- Run the following command from inside the Harmonic Algorithm directory:
stack --install-ghc build
You can now run The Harmonic Algorithm by executing the following command from
inside it's directory:
stack exec theHarmonicAlgorithm-exe
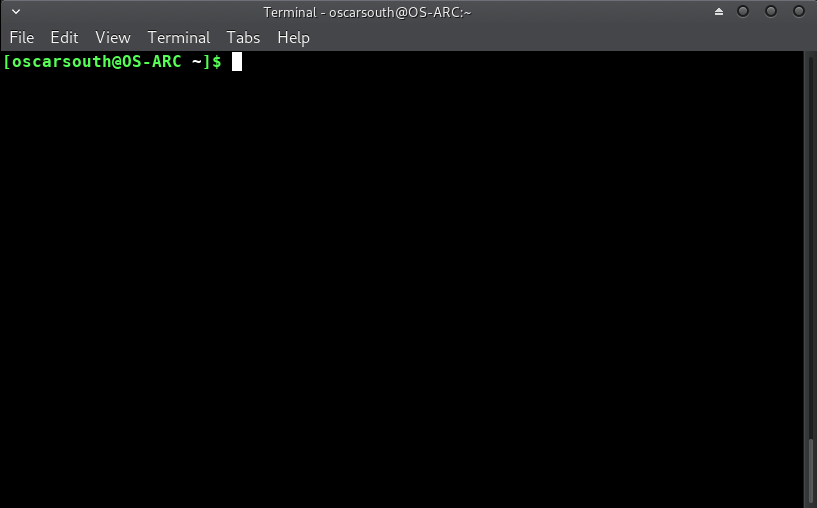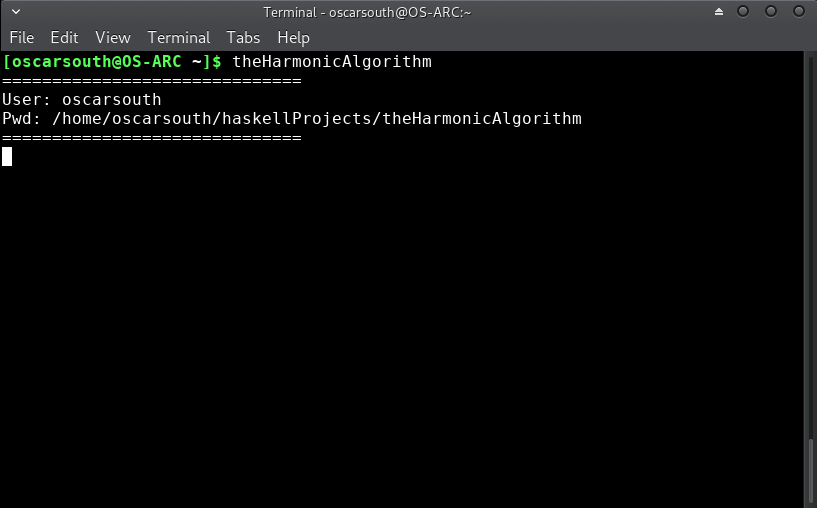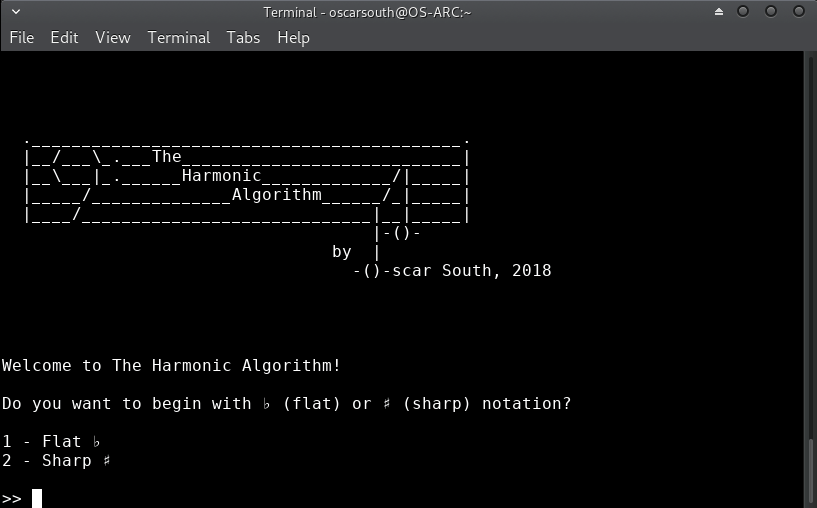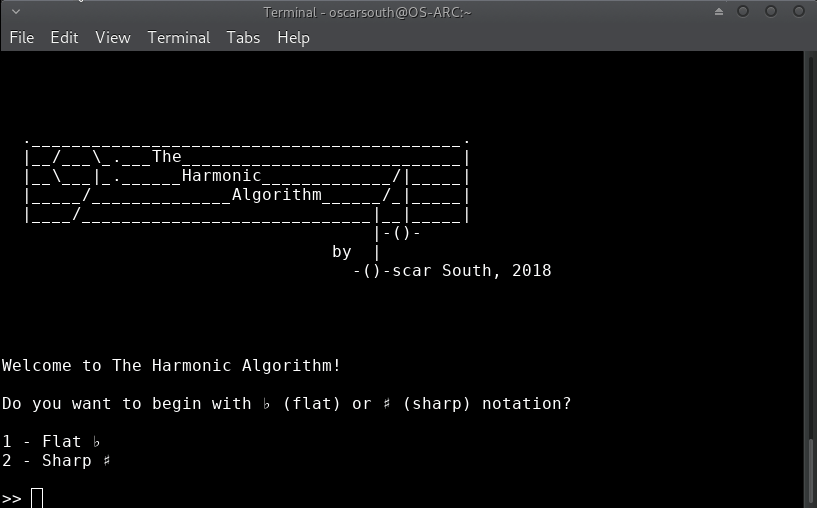
Initially on loading the app, the R interpreter will be booted and required libraries loaded. The Harmonic Algorithm is written primarily in Haskell and interfaces with the R statistical computation language for enhanced dataframe manipulation and plotting functionality:
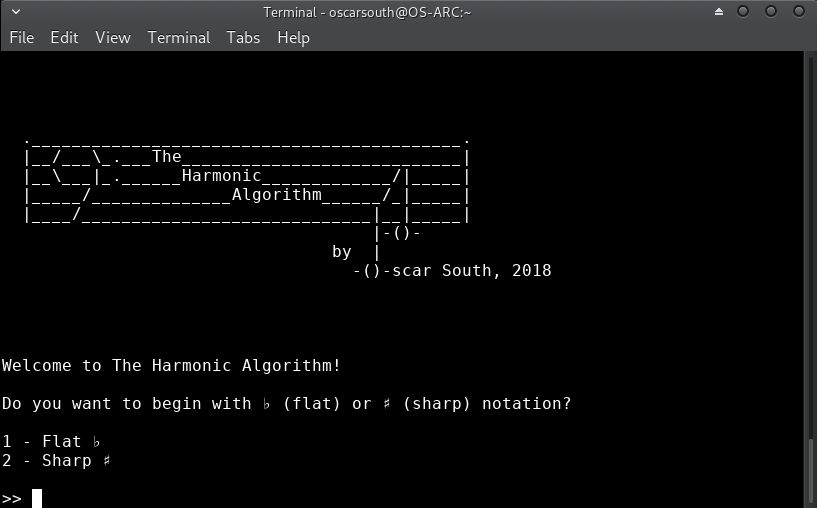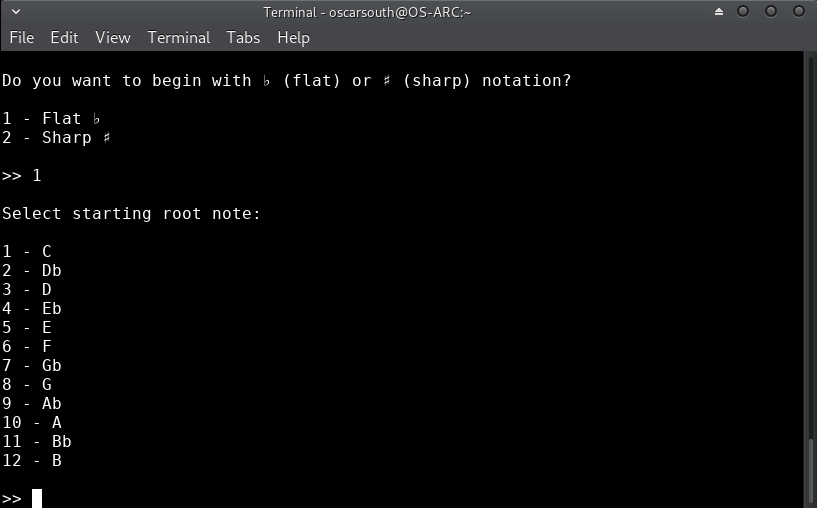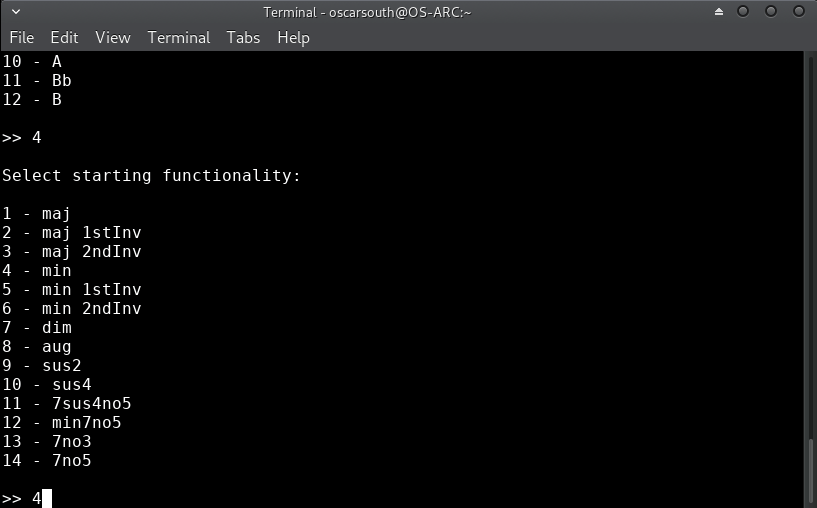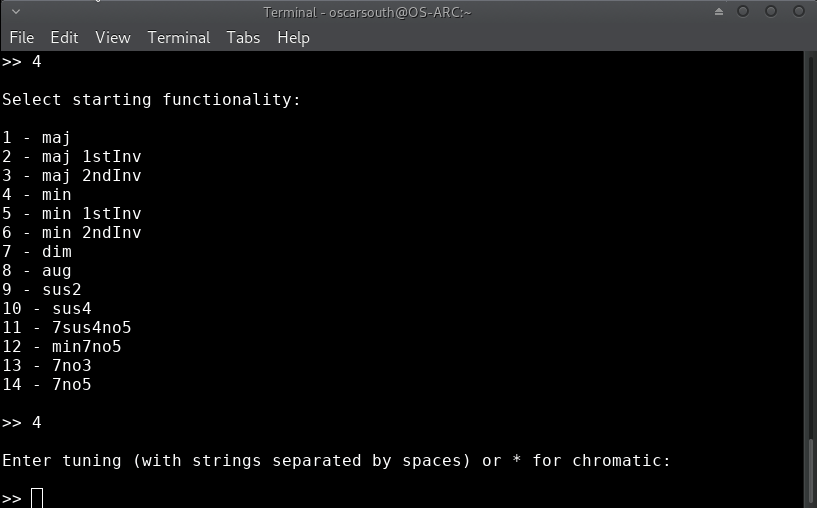
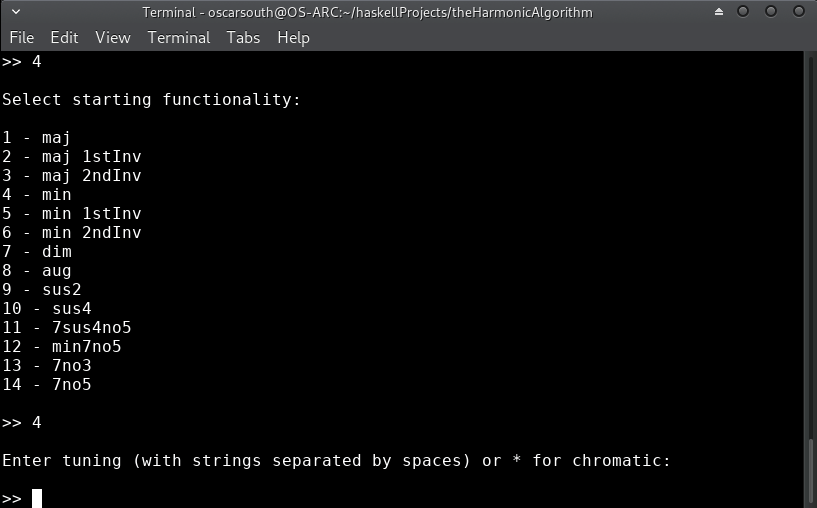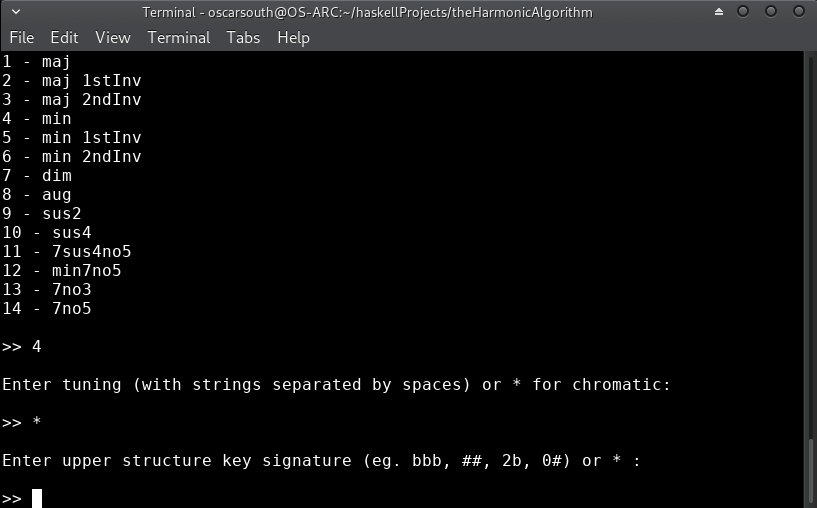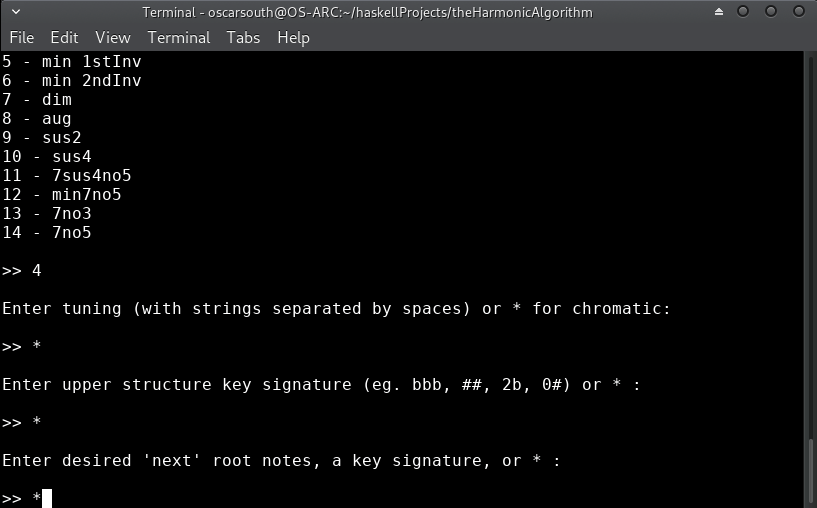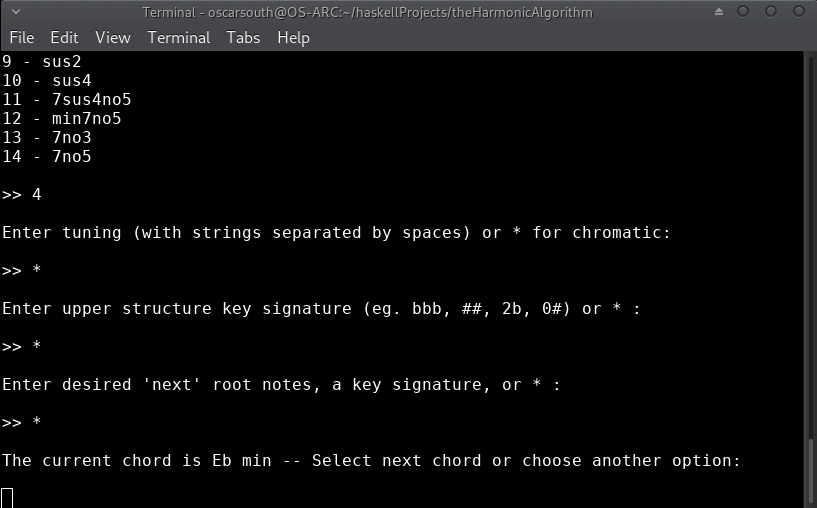
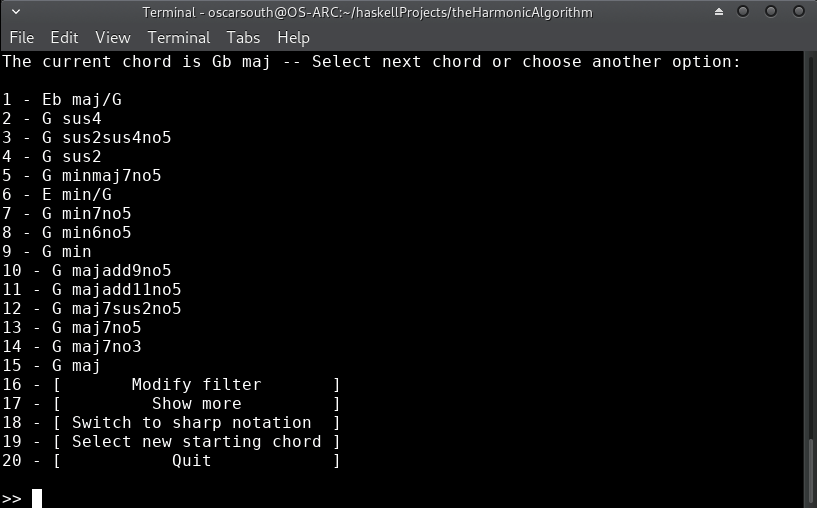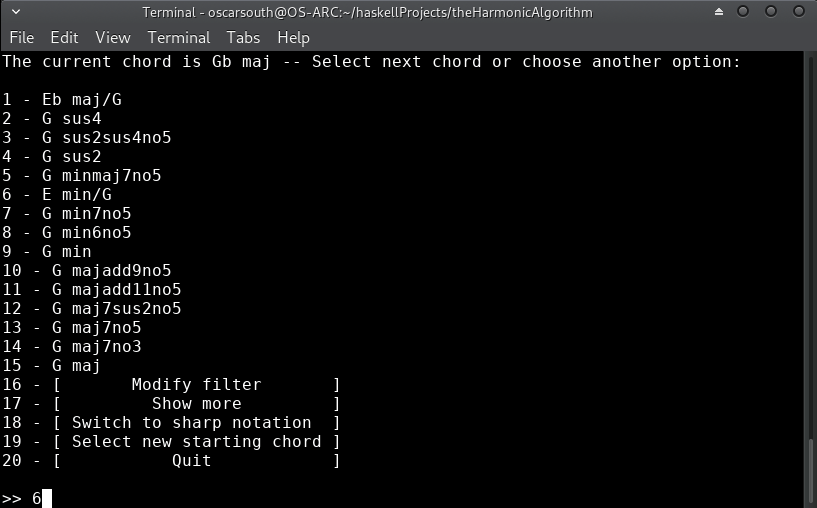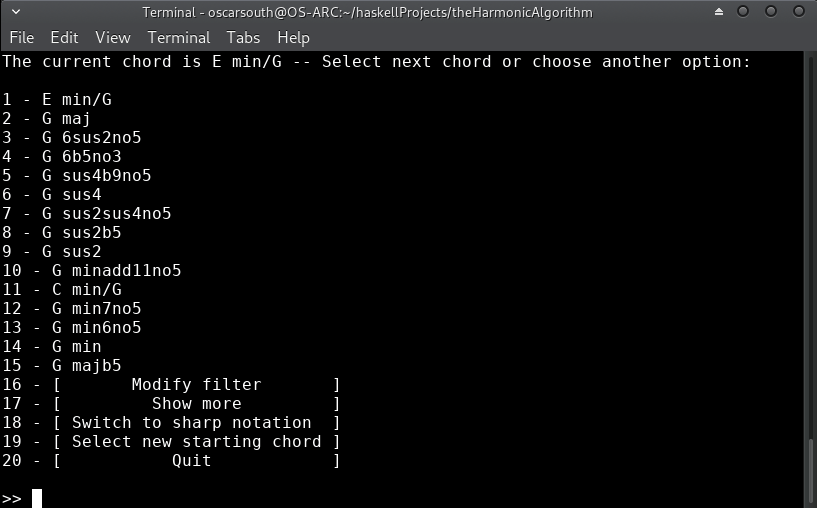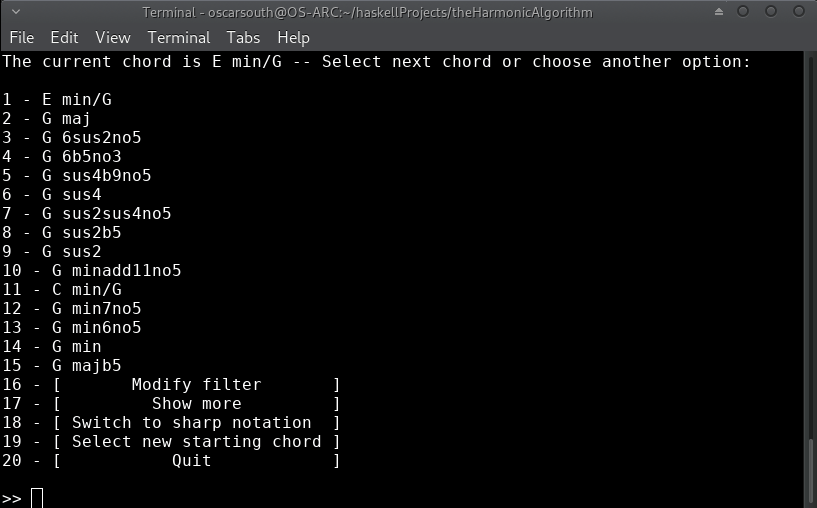
After a moment, the title screen will load and you will be asked a couple of multiple choice questions relating to what enharmonic (flat or sharp) notation style you would prefer to begin with as well as which root note and upper musical structure will be chosen as the initial state.
In this example, flat notation with the starting chord of Eb minor is chosen:
The next selections are related to how the list of 'next' harmonic choices will be filtered down. These can be modified at any time during interactive usage of the app.
-
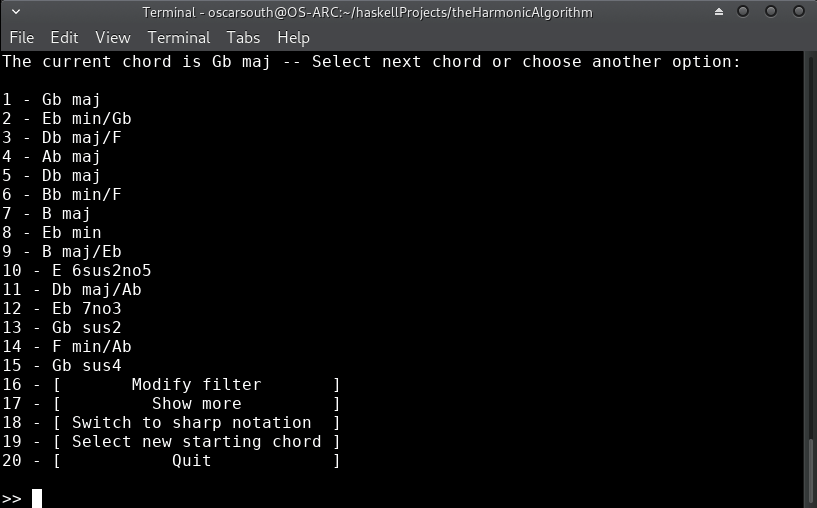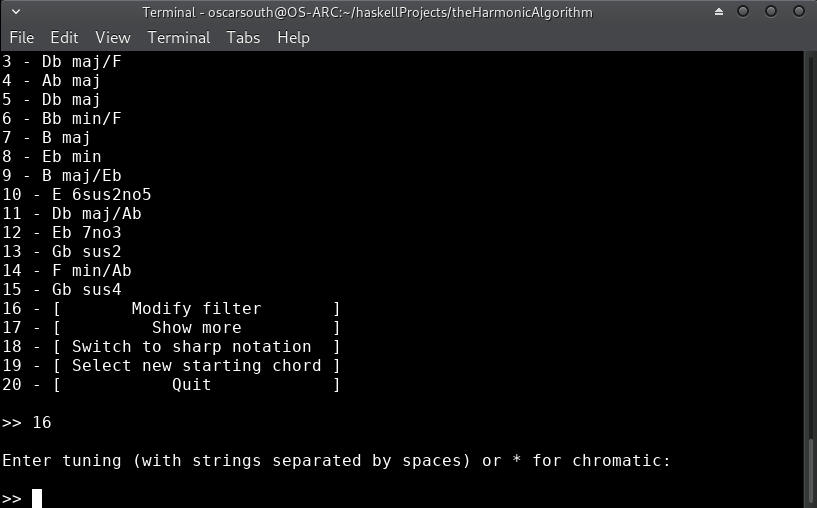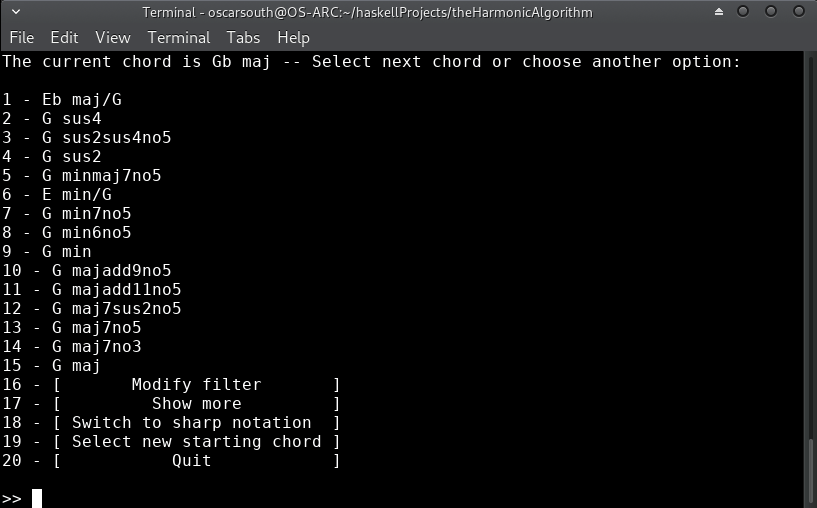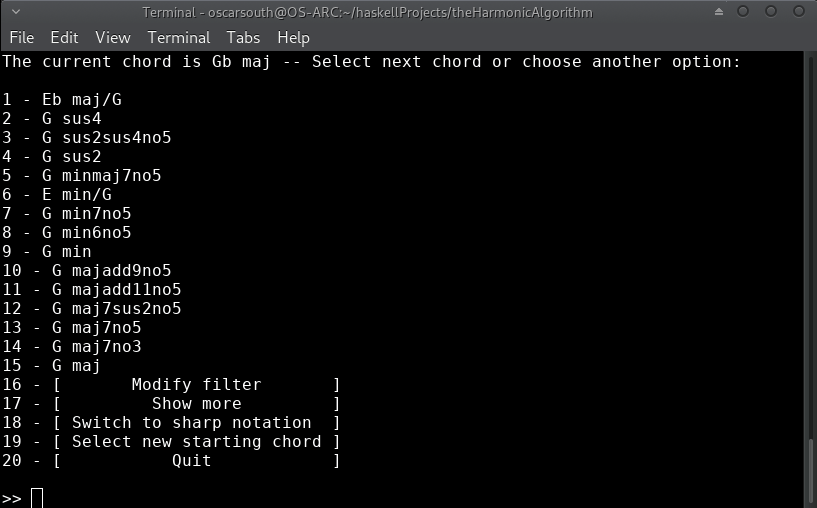
Filtering by overtones or pitch set. This filter will limit possible harmonic choices to those existing inside a set of pitches. This could represent the available overtones of an instrument or a superimposed pitchclass set. To derive overtones of a tuning, simply type the fundamental pitches seperated by spaces (eg.
E A D Gfor standard electric bass). To add individual pitches, append the 'prime' (') symbol. Overtones and individual pitchclasses can be combined freely (eg. the E minor blues scale consisting of the overtones of a G and additional pitches E, A & A#:G E' A' A#'). **for most uses cases where simple filtering by key or root notes is required, it is best to enter*for this filter. -
Filtering by key. This filter will remove any items from the overtones/ pitch class set which are not present in the key specified. Define this filter by by entering a key signature (
bb,###,4b,0#). or alternatively a key can be named (C,F#m,Bb). **where modifying the specified pitchclass set is undesired, enter*. -
Filtering by root notes. This filter will limit the bass note of harmonic choices to a set of pitch classes or key. Define this filter by entering a set of pitches seperated by spaces (
E F# G) or a key signature (1b,#). **note that this filter exists independently of filtering by pitch class set and key and can (intentially) cause stuctures with root notes outside the limits of the upper structure filters to be displayed. To strictly limit by a key, enter the same key signature as entered for the key filter.
Results can also be left unfiltered by entering the wild card * symbol for all
filters. In this case, all filters are left open:
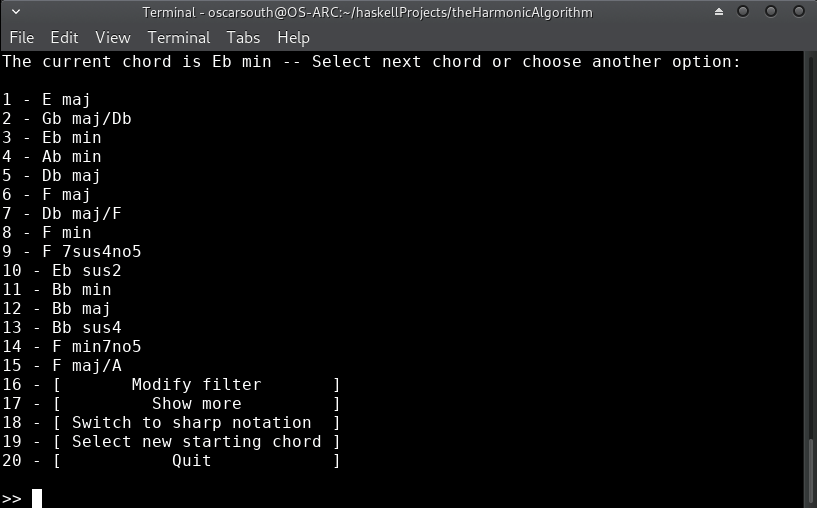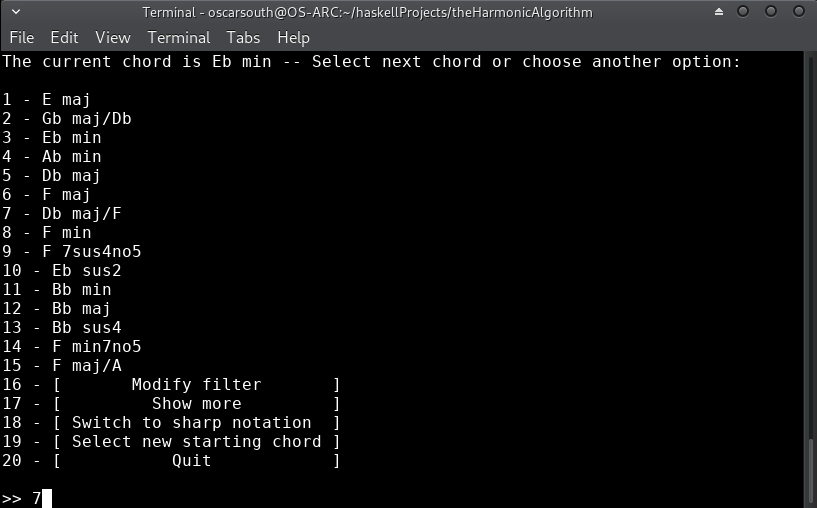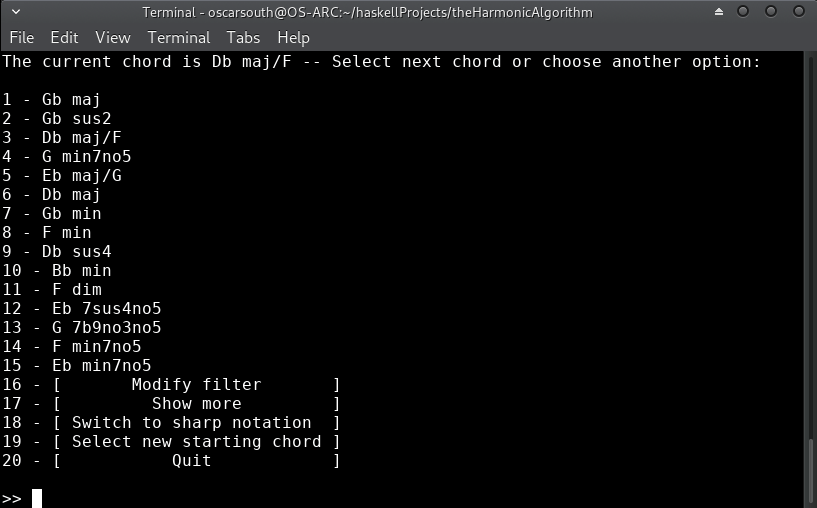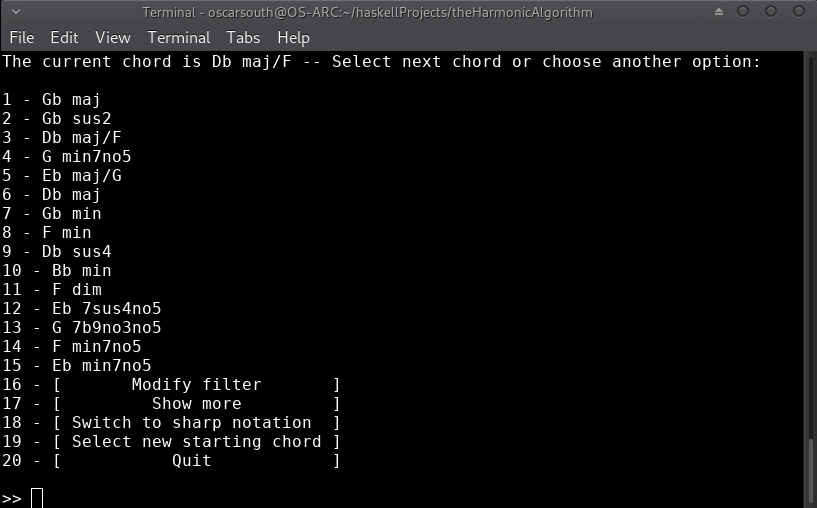
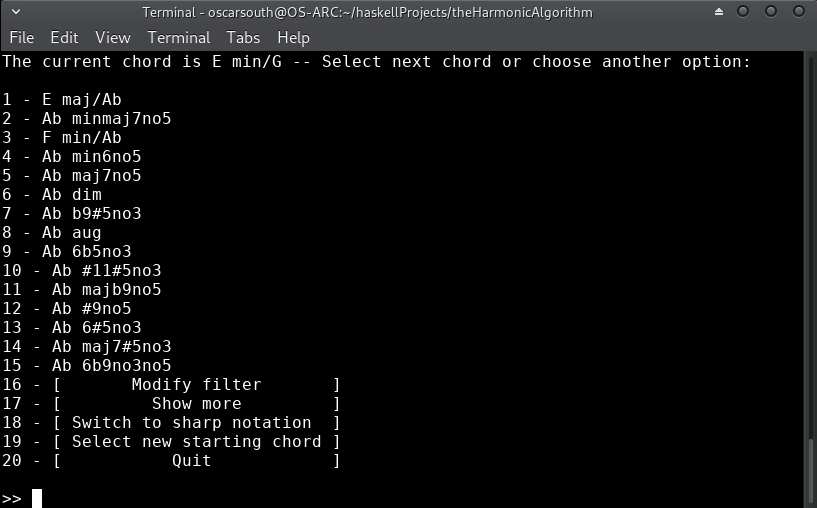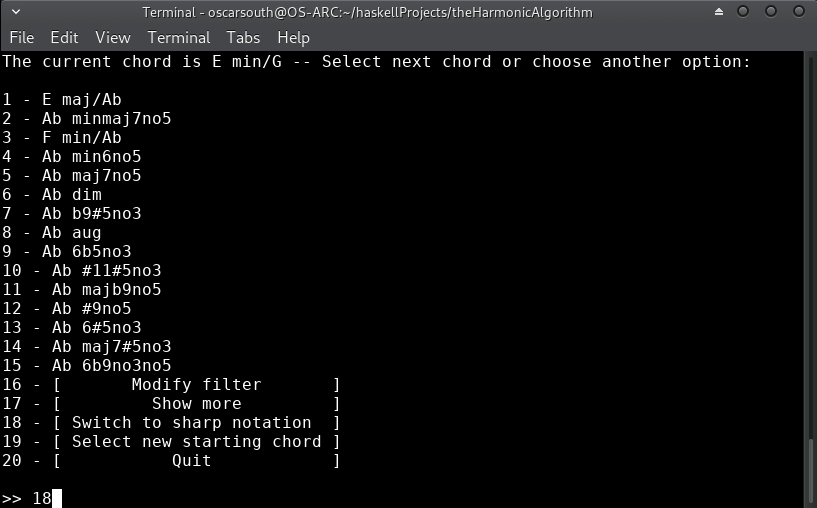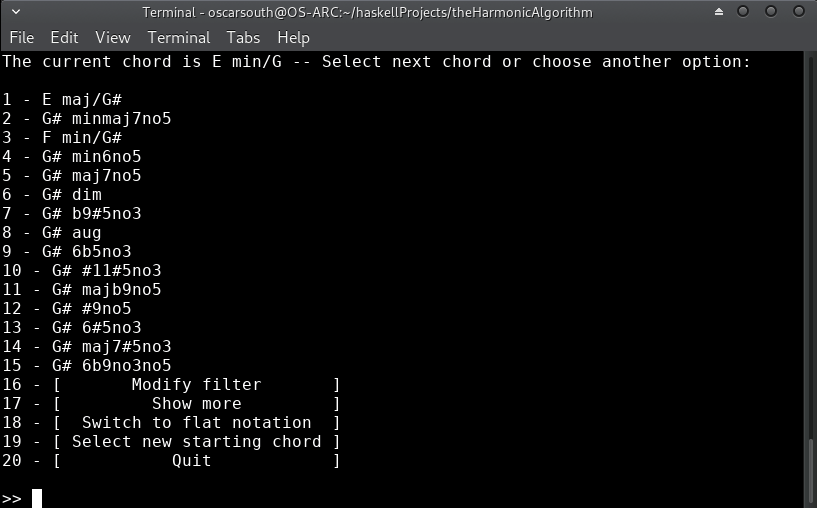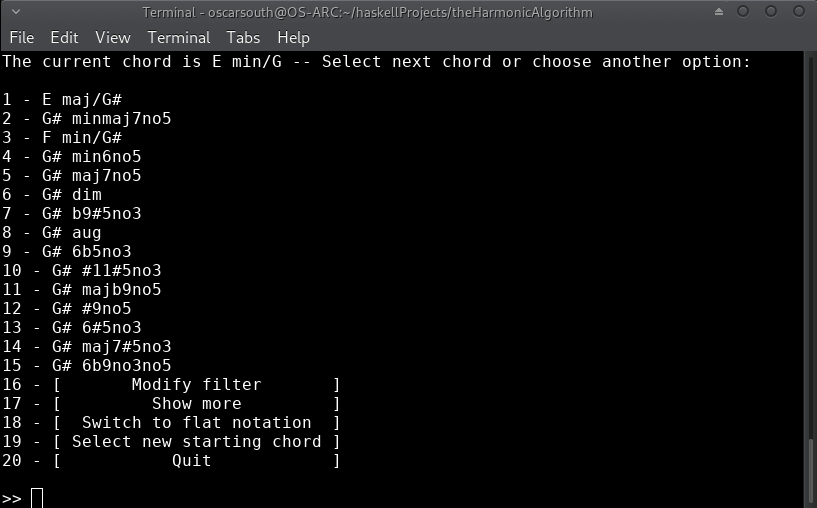
After taking a few moments to train the recommendation model, the initial list of 'next' harmonic choices is displayed along with a few additional options. The possibilities presented are ranked on a combination of learned behavior from the J.S.Bach Chorale harmonisations used to train the model as well as derived dissonance ranking. The model takes prescidence where there is conflict.
The first ranking would be assuming that our current chord is acting as a iii in the key of B. Let's remain in Ebm for now. I've chosen option 7 of Db/F (a VII in Eb voiced in first inversion):
The recommentation system will suggest unique possibilties after each cadence, depending deterministically on recent harmonic motions. It is also possible to remain on the same chord, which is itself a decision and will thus influence recommendations for the next successive movements.
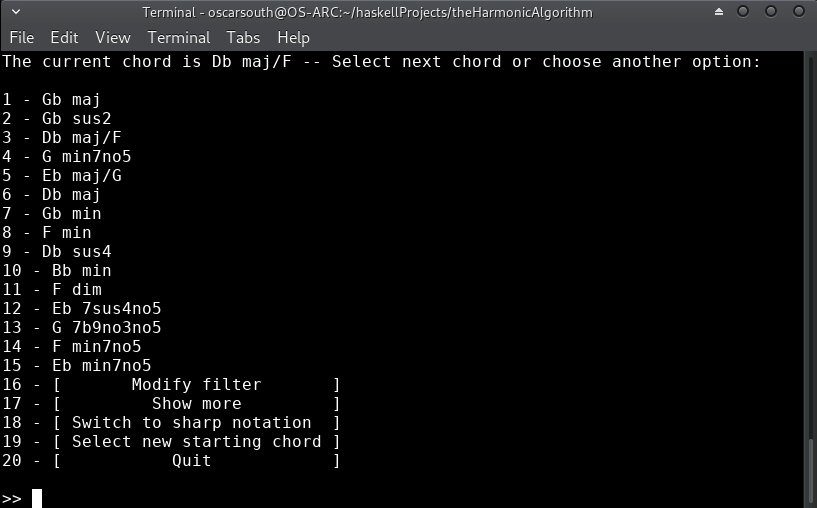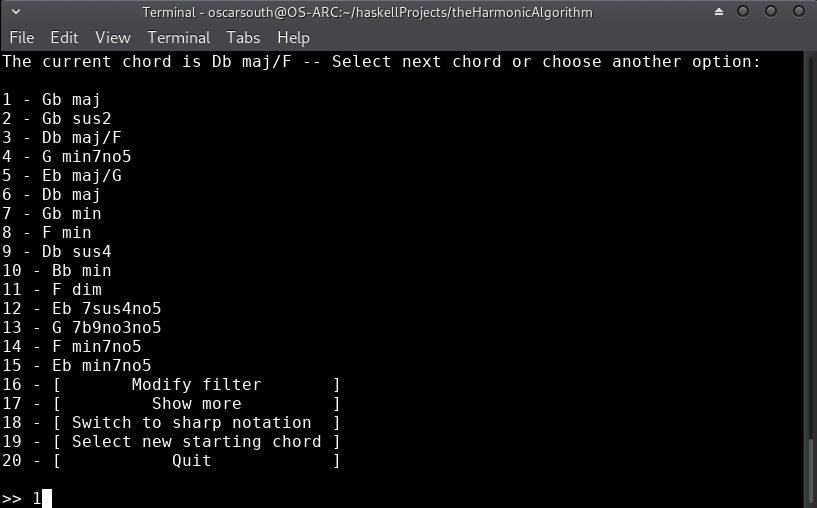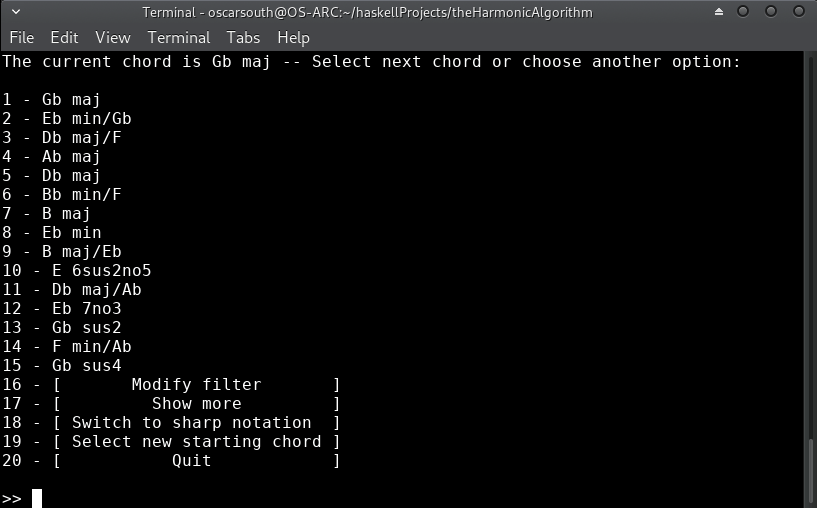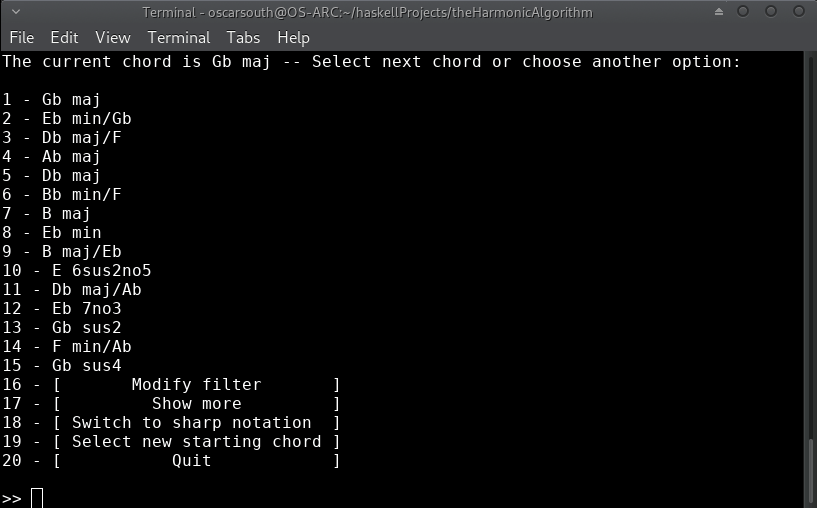
Let's continue with option 1 for an upwards root motion to the III chord (Gb):
Let's maintain the ascending root motion, this time chromatically. In order to see what possibilities are available, I'll filter down the results to show only structures with a G in the bass while keeping the upper tones chromatic:
This gives us some interesting options! Let's modulate! I'm going to choose option 6 and think of it as a v chord (in first inversion) in A minor:
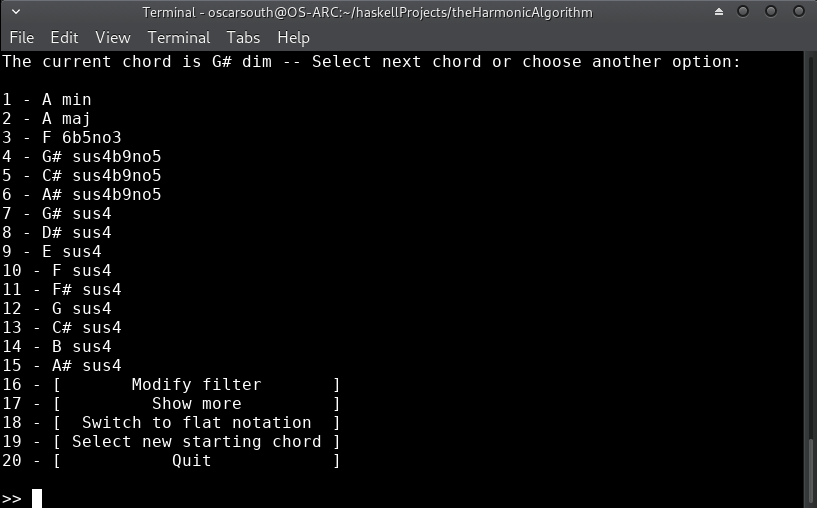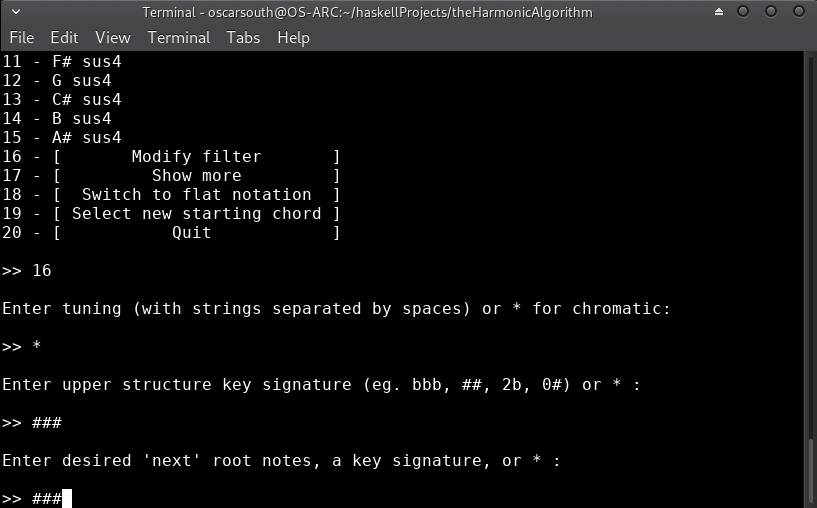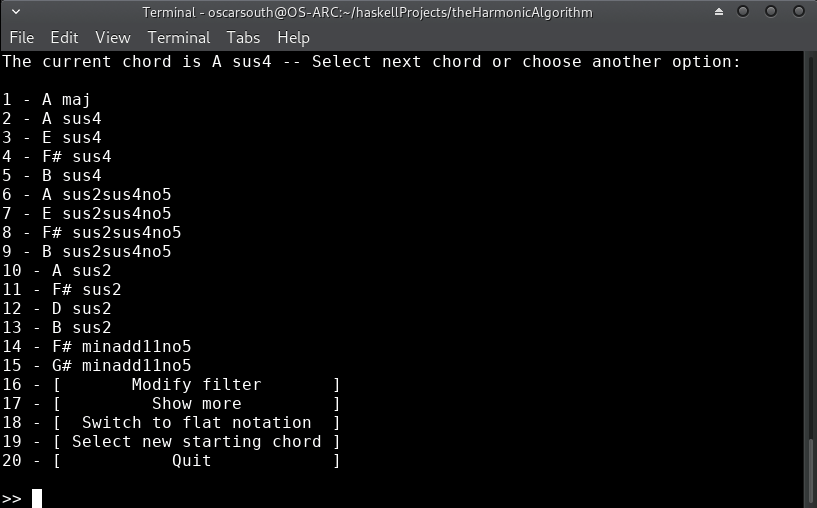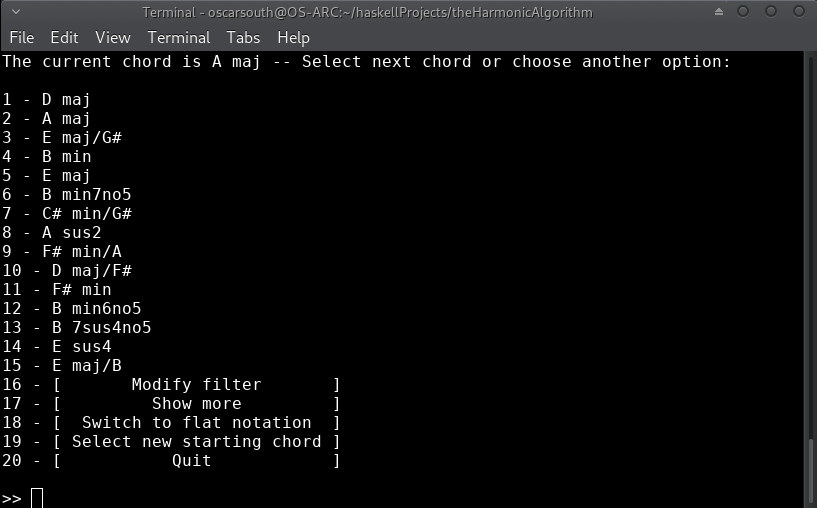
The previous minor v is a weak chord to modulate from, however we're starting to build tension through root motion. Let's modify our filters and see if there is an interesting choice with an upper structure in the key of A minor that will let us continue our chromatic root motion through G#:
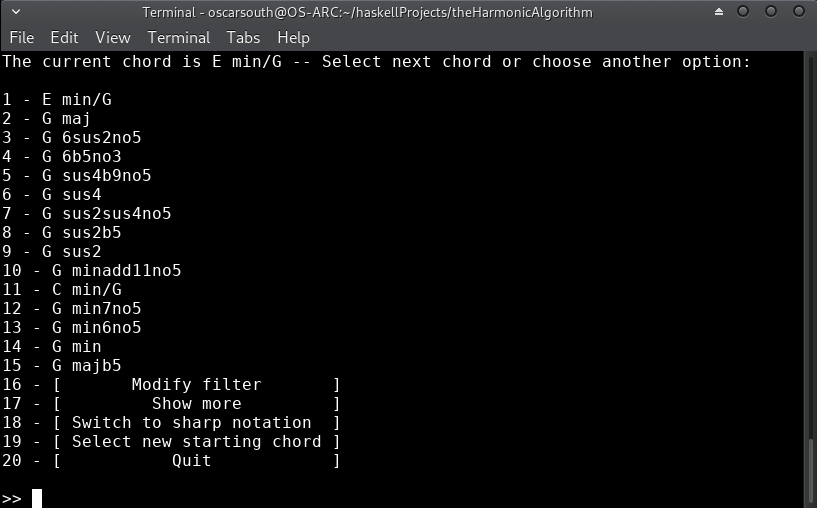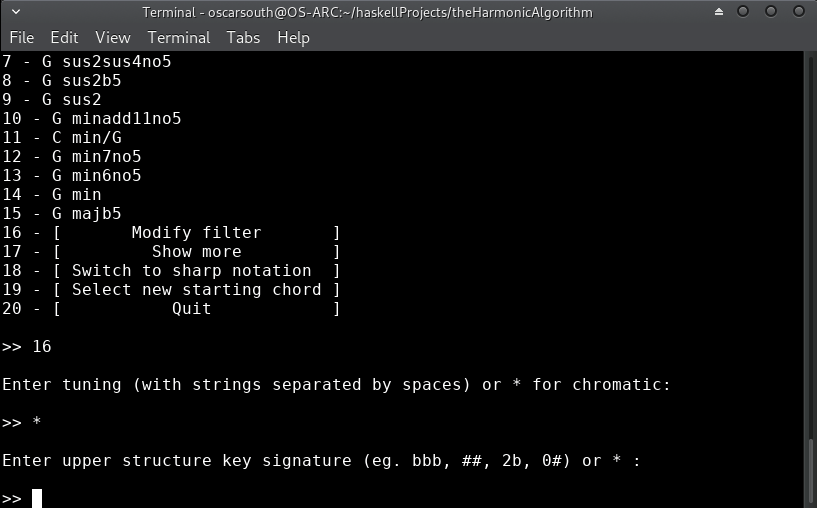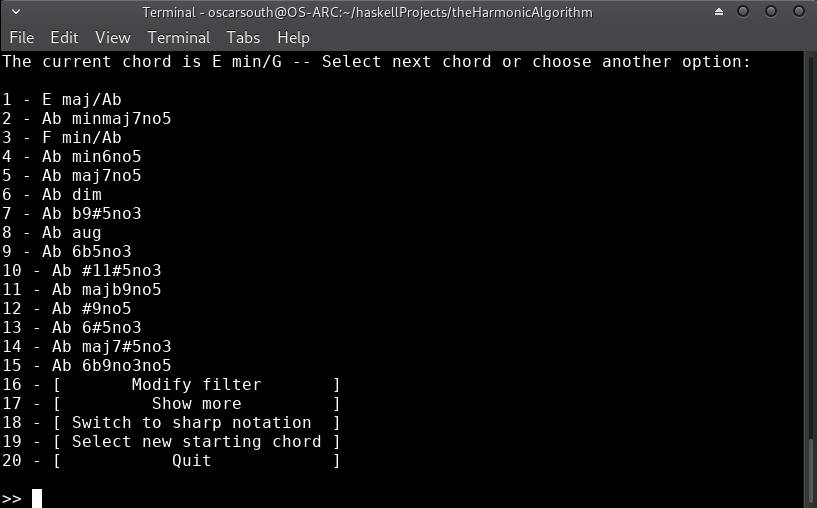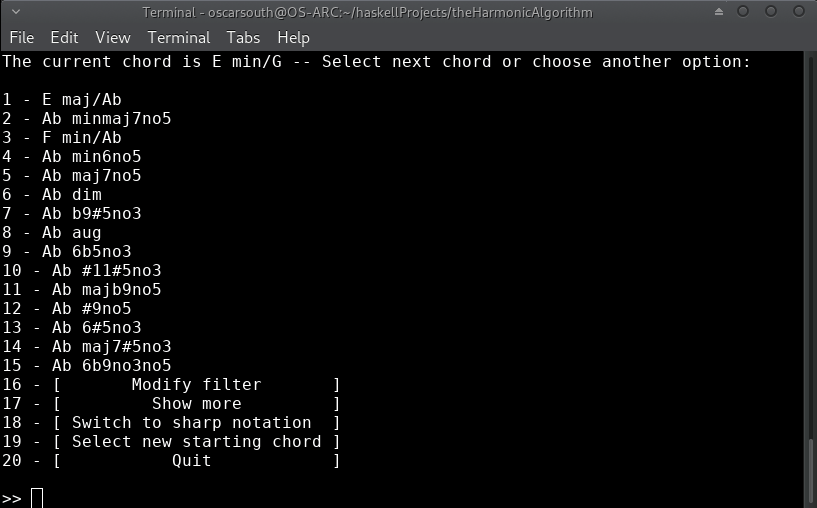
I'd also prefer to read this in sharp enharmonic notation, so I'll switch over:
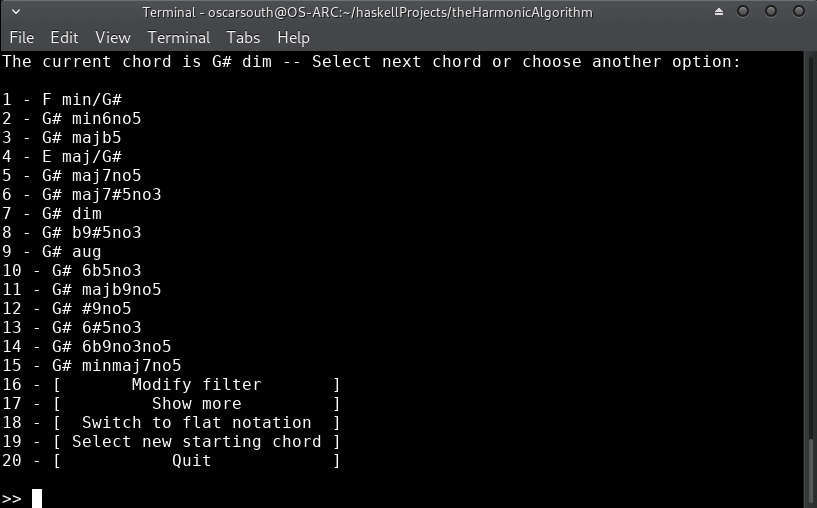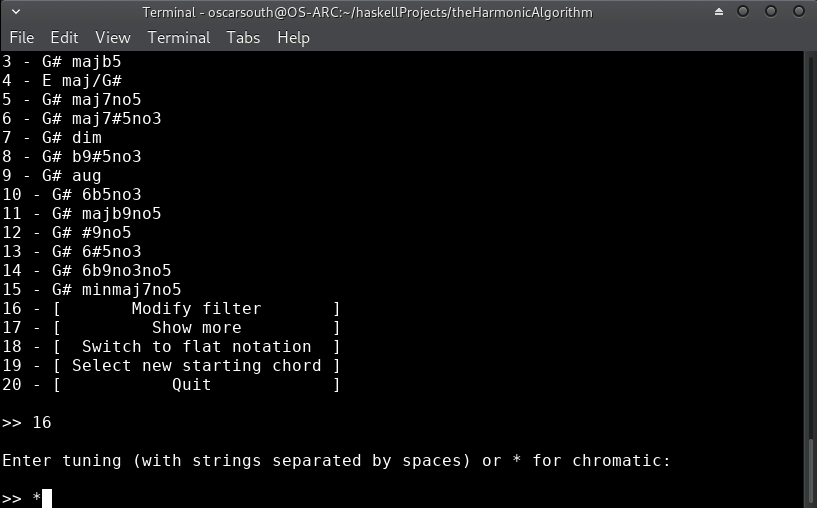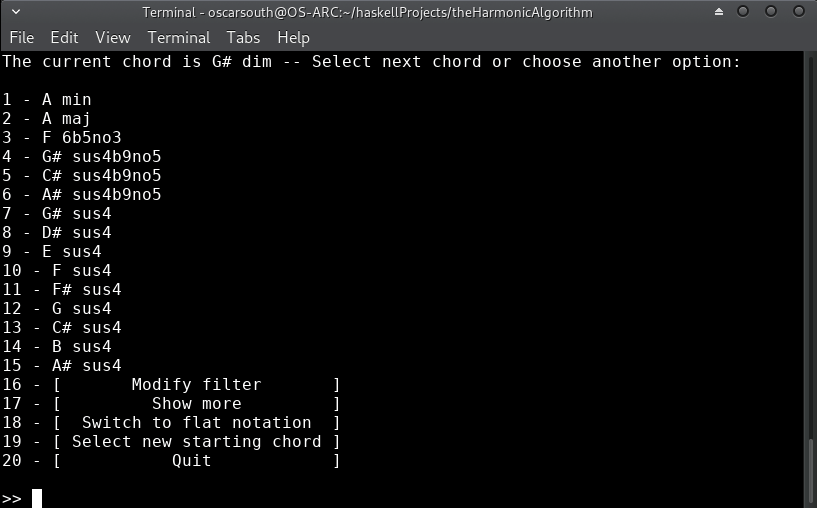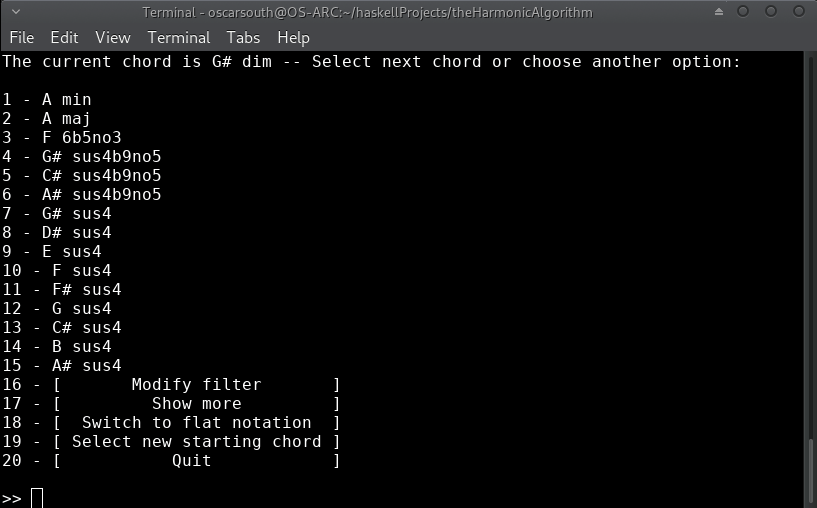
Wow! Some very interesting choices here! The obvious choice would be E/G#, representing a V in first inversion leading into the tonic of Am. This seems too obvious though. Let's go with G# diminished to really build tension as we ascend into the new key:
We know we want to modulate to an A root, so we need to modify the filters.
Since there's already a strong harmonic pull from G# diminished to an A,
lets just set all filters to * and see what the algorithm recommends:
Cool! A minor and A major are our top two recommendations! J.S.Bach really knew what he was doing!
Let's diverge from minor keys and resolve to the major. I'll filter down to diatonic recommendations inside A major and move into the major tonic through a sus4 to add a little ambiguity to the transition:
We're now in the new key and have a variety of choices for where to go next!
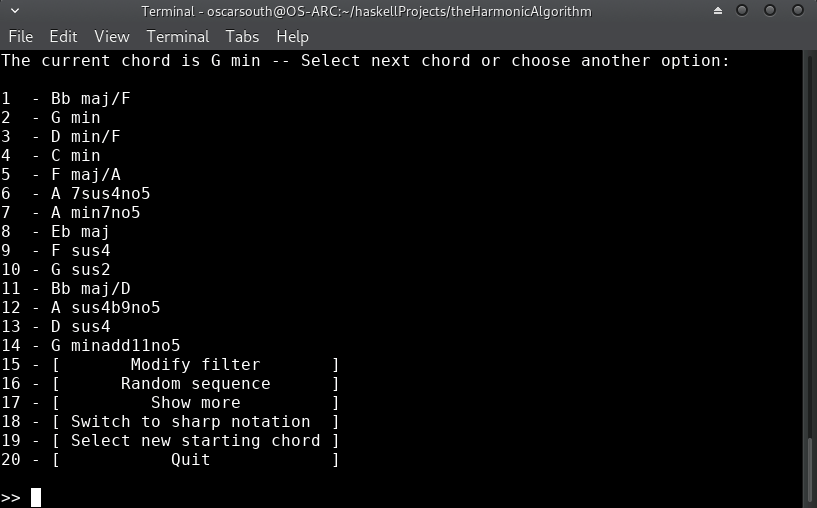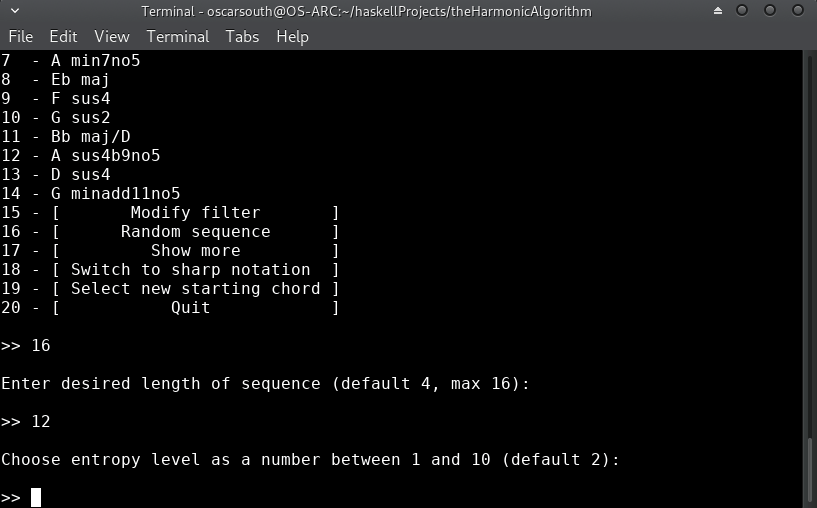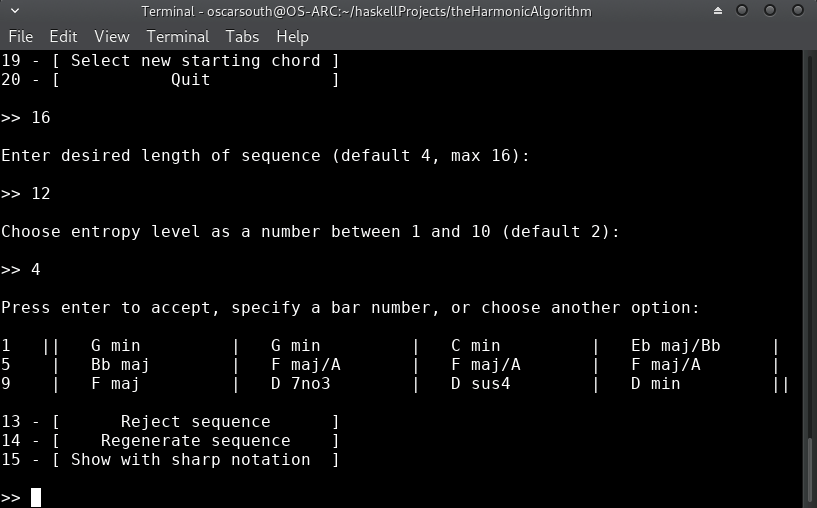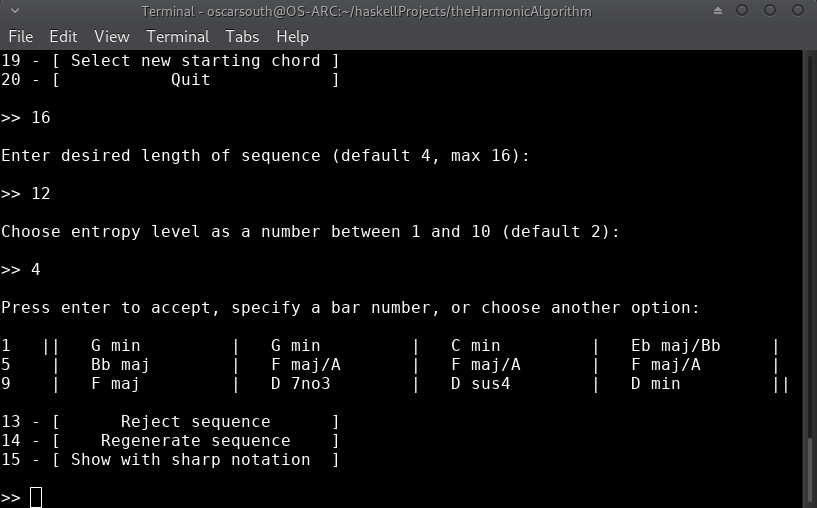
New in Version 1.0.1.0 is the ability to generate Random Sequences of harmonic movement!
Random sequences allow the performer/composer to traverse deterministic space (move through musical cadences!) at a much faster rate and give a 'higher up' viewpoint to the character and nature of harmonic motion in a given musical context. The performer/composer can then 'jump in' to any point of the generated sequence and move through musical space in 'blocks' of harmony.
Let me know if you have any feature suggestions or comments in general and feel free to get in touch through this repository's 'Issues' section: https://github.com/OscarSouth/theHarmonicAlgorithm/issues
Alternatively, use the contact form for my main performance project 'UDAGAN': https://UDAGANuniverse.com/contact
Oscar