This software can generate geometry problems of various difficulties suitable for mathematical contests including the IMO. See the list of already proposed problems.
It was developed as my master thesis.
An example of a non-trivial generated problem whose wording, and figure were entirely generated by the software:
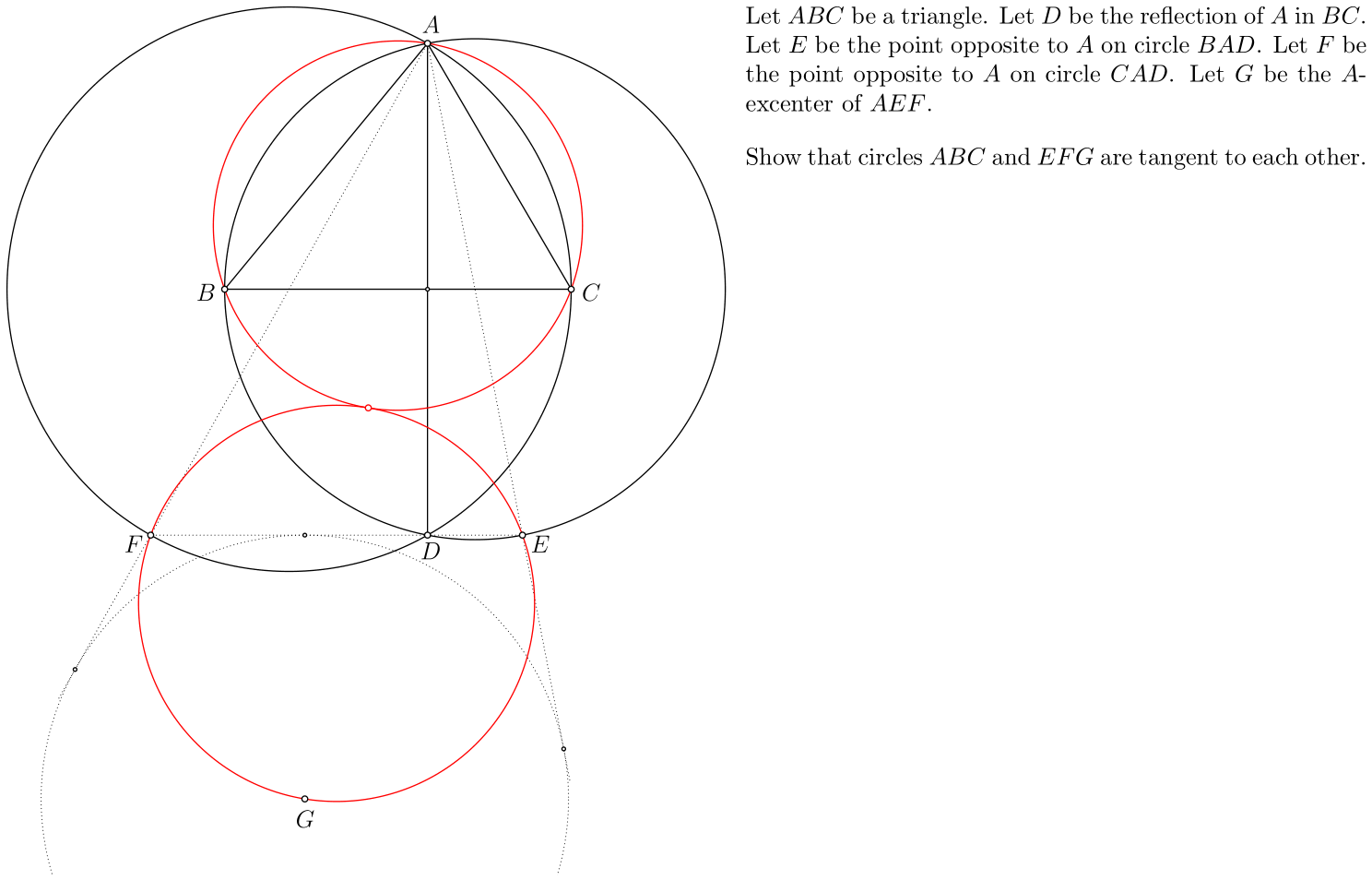
Here is a list of problems that have been created with the aid of the software. Many of them have been generated during the "big experiment" described in the thesis, page 56.
-
IMO 2022, P4 (statement) -- the story how the software helped to generate it is in the solution thread
-
ISL 2020, G6 (statement) -- generated in the big experiment and stated without modification
-
ISL 2020, G3 (statement) -- generated in the big experiment in a version where D was the reflection of B in the midpoint of AC, then generalized after solving
-
IGO 2020, A2 (statement) -- generated in the big experiment and stated without modification
-
MEMO 2021, I3 (statement) -- generated in the big experiment in a version where D was the projection of A onto BC, then generalized after solving
-
CPS 2021, P2 (statement) -- generated in the big experiment and stated without modification
-
CPS 2020, P1 (statement) -- generated in the big experiment and slightly restated
(The list is not exhaustive, it does not include many easier problems used in Czech-Slovak local competitions)
See also the examples from Appendix of the thesis.
There are two major steps:
The main idea is to start with a geometry configuration (such as a triangle) and keep adding new objects (lines, points, circles) into it.
The algorithm sounds simple, but deep down, the algorithm turns out to be fairly complex. The combinatorial explosion is massive and one needs to do a lot of tricks to mitigate it.
The theorems are then verified probabilistically using analytic geometry. In practice, if a geometry theorem holds in 5 random figures, it must holds all the time.
This is done by utilizing geometry theorem proving methods. The main idea of this part is this: If we can prove a theorem, it is not hard enough, as we aim for the hardest problems.
Therefore, the prover is built to prove as many theorems as quickly as possible, unlike the standard problem in theorem proving, which is to prove as many theorems as possible without caring too much about how long it takes.
There also is a heuristic ranking system. The 4 rated aspects are selected based on the author's years of experience in writing geometry problems.
For technical notes regarding the code, installation, and running, see this.
If you are interested in my project, or if you have any other question, contact me via email.