/ICML10

MATLAB scripts to reproduce the results of our ICML 2010 paper

Primary LanguageMATLAB

Support Page for "A Fast Augmented Lagrangian Algorithm for Learning Low-Rank Matrices"

Demo 1: Low-rank matrix completion

This demo shows that the proposed M-DAL algorithm can perform matrix completion of 10,000x10,000 (rank 10) matrix from 1.2M observations very fast (roughly 5 min on a 3.1GHz Opteron (quad-core) machine)

Before running this demo, you need to mex PROPACK routines. On a linux machine what you have to do is (hopefully) just to run the script setup.m in the root folder after extracting the archives.

 setup

If this doesn't work, this demo might be very slow. But you can still run Demo 2 and Demo 3 without PROPACK.

To run the algorithm, just type

 cd demo1
 demo1

The first few lines of the script demo1.m looks like this:

n=10000;    % size of the unknown matrix
m=1200000;  % number of observations
k=10;       % true rank of the unknown matrix
lambda = [1000 700 500 300 200 150 100];
            % regularization constant
eta=10;     % step-size parameter
nrep=10;    % number of repetition

memo=test_matrix_completion(n,m,k,lambda,eta,nrep);

If you also want to try rank 20, just type

 k=20;        % True rank of the unknown matrix
 m=2400000;   % Number of observations
 lambda=[2000 1500 1200 1000 700 500 400 300 200 150 120 100];
 memo=test_matrix_completion(n,m,k,lambda,eta,nrep);

The output (for the default rank 10) should look like this:

lambda   time(s)         #iter_out       #iter_in        #svd            rank            error
----------------------------------------------------------------------------------------------------------------
1000     30.5(± 2.29)    5(± 0)          8(± 0)          32(± 0)         3(± 0)          0.0162(± 0.00369) 
700      71.4(± 4.66)    11(± 0)         18(± 0)         71(± 0)         5(± 0)          0.0132(± 0.00174) 
500      114(± 5.93)     17(± 0)         28(± 0)         110(± 0)        6.40(± 0.516)   0.0112(± 0.00208) 
300      161(± 6.79)     23(± 0)         38.4(± 0.699)   151(± 3.07)     8(± 0)          0.00868(± 0.00065) 
200      202(± 6.50)     29(± 0)         48.4(± 0.699)   190(± 3.07)     9(± 0)          0.0079(± 0.000407) 
150      237(± 6.83)     35(± 0)         58.4(± 0.699)   231(± 3.07)     9(± 0)          0.00519(± 0.000343) 
100      296(± 7.26)     41(± 0)         69.8(± 1.48)    275(± 4.69)     10(± 0)         0.0075(± 0.000209)

Demo 2: Synthetic matrix classification

The task here is to classify 64 x 64 matrices where the true classifier coefficient is a symmetric rank 16 matrix. The proposed M-DAL algorithm is clearly 10-30 times faster than previous algorithms.

To run the script, just type

 cd demo2
 demo2

The first few lines of demo2.m looks like this:

m = 1000;      % Number of samples
n = 64;        % Dimension
k = 16;        % True rank
lambda = 800;  % Regularization constant
algos  = {'dal','lrds','ag','projgrad',};
               % Algorithms
nrep   = 10;   % Number of repetitions

memo = test_matrix_classification(m, n, k, lambda, algos, nrep);

If you want to get the results quickly set nrep to 2

 nrep = 2;

(2 is minimal to compute the standard deviation).

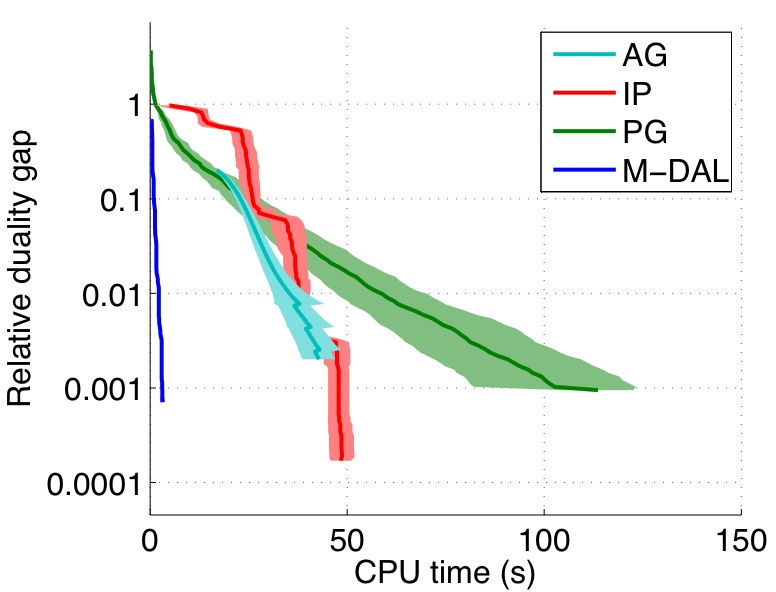
After running the script, you will get a plot like this:

demo2

Here, AG is the accelerated gradient method proposed in Ji & Ye 2009, IP is the interior-point algorithm proposed in Tomioka & Aihara 2007, PG is the projected gradient method proposed in Tomioka & Sugiyama 2008.

The script for AG method used here differs from the script written by Ji & Ye only in that it also outputs computation time as follows:

46c46
< function [Wp,b,fval_vec,itr_counter] = accel_grad_mc(Xtrain,Ytrain,lambda,opt)
---
> function [Wp,b,fval_vec,time_vec,itr_counter] = accel_grad_mc(Xtrain,Ytrain,lambda,opt)
94a95,96
> time_vec = zeros(1,max_itr);
> time0 = cputime;
124a127
>     time_vec(itr_counter) = cputime-time0;

Demo 3: BCI classification with multiple matrices

The task in this experiment is taken from BCI competition 2003 dataset IV. The task is to predict the laterality (left or right) of the upcoming finger movement from EEG signal before it is executed.

Each input data is a short segment of multivariate time-series and is stored in a 28 (channels) x 50 (time points) matrix. We preprocessed each input into three matrices as follows (See Tomioka & Müller 2010 for details)

  • First order component (low-pass filtered at 20Hz) : [28x50]
  • Second order (alpha-band) component (band-pass filtered at 7-15Hz) : [28x28]
  • Second order (beta-band) component (band-pass filtered at 15-30Hz) : [28x28]

This demo comes with preprocessed train-/test- datasets. To run the script, just

 cd demo3
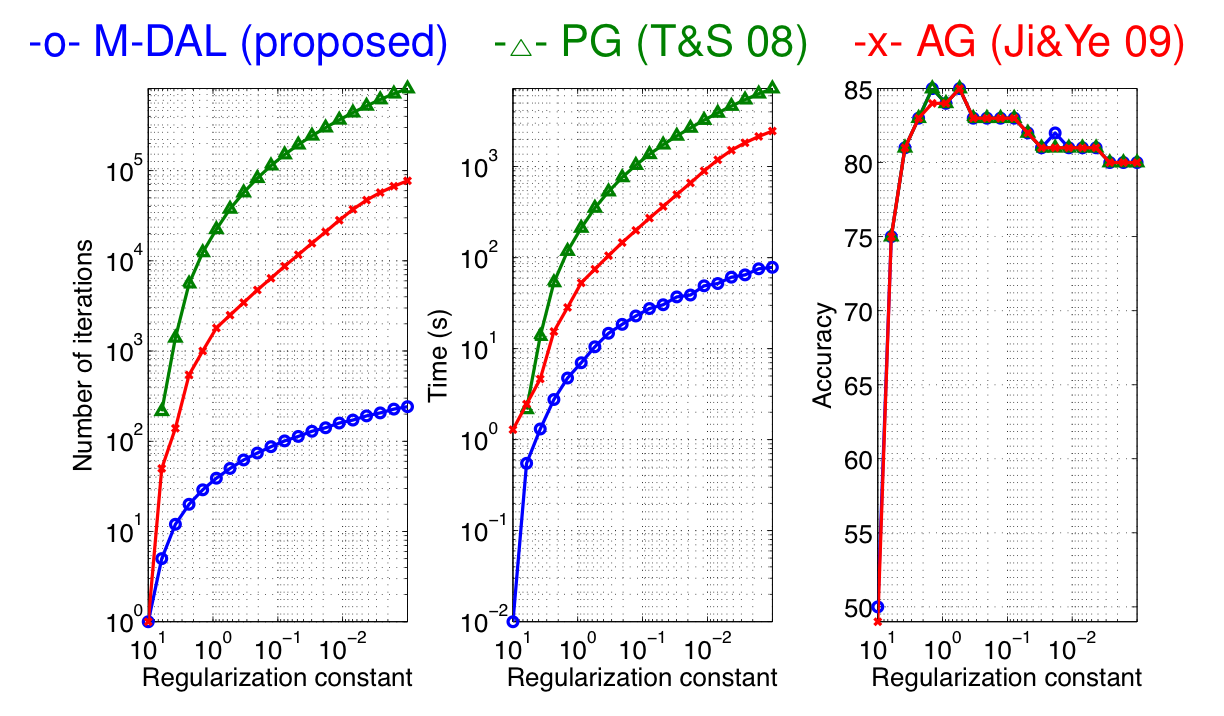
 demo3

The figure below shows that the proposed M-DAL algorithm is roughly 10-100 times faster than the previous AG and PG approaches; IP was not included because it was not straightforward to extend the IP approach in Tomioka & Aihara (2007) to multiple-matrix case (just concatenating matrices along the diagonal makes the problem-size unnecessarily large and is unpractical).

bci

In the figure, the number of iterations, CPU time, and the test accuracy are plotted against the regularization constant. Note that we use a warm start strategy (i.e., we use the solution obtained for one regularization constant to train the next model with a smaller regularization constant). Accordingly the costs (#steps & CPU time) are accumulated from large lambda to small lambda. All algorithms were terminated when the relative duality gap (= (primal obj - dual obj)/primal obj) fell below 1e-3.

The script accel_grad_mmc.m differs from the original as follows

  • It supports multiple input matrices as cell matrices.
  • It computes duality gap (as a stopping criterion).
  • Some speedups (vectorization). The exact diff can be found here.

Contact

Any kind of feedbacks (comments, bug reports, etc) are appreciated. Email: tomioka [AT] ttic.edu

References