Grid Workflows

This repository contains examples of Grid workflows. Each workflow in this repository showcases different API aspects, concepts and techniques to achieve advanced infrastructure configurations and application setup while trying to keep things around 10 lines of code.

WARNING: Grid (currently version 1.0.3) is still under development and not all protection mechanisms are activated. Before you start please familiarize yourself with the security model and verify you rsecurity settings as described here: https://github.com/PhilippLgh/grid-core

Examples

Hello Grid - Grid's version of "hello world"
Ethereum 2.0 with Prysm - Validator, Beaconchain, TestEth.. all you need to get started
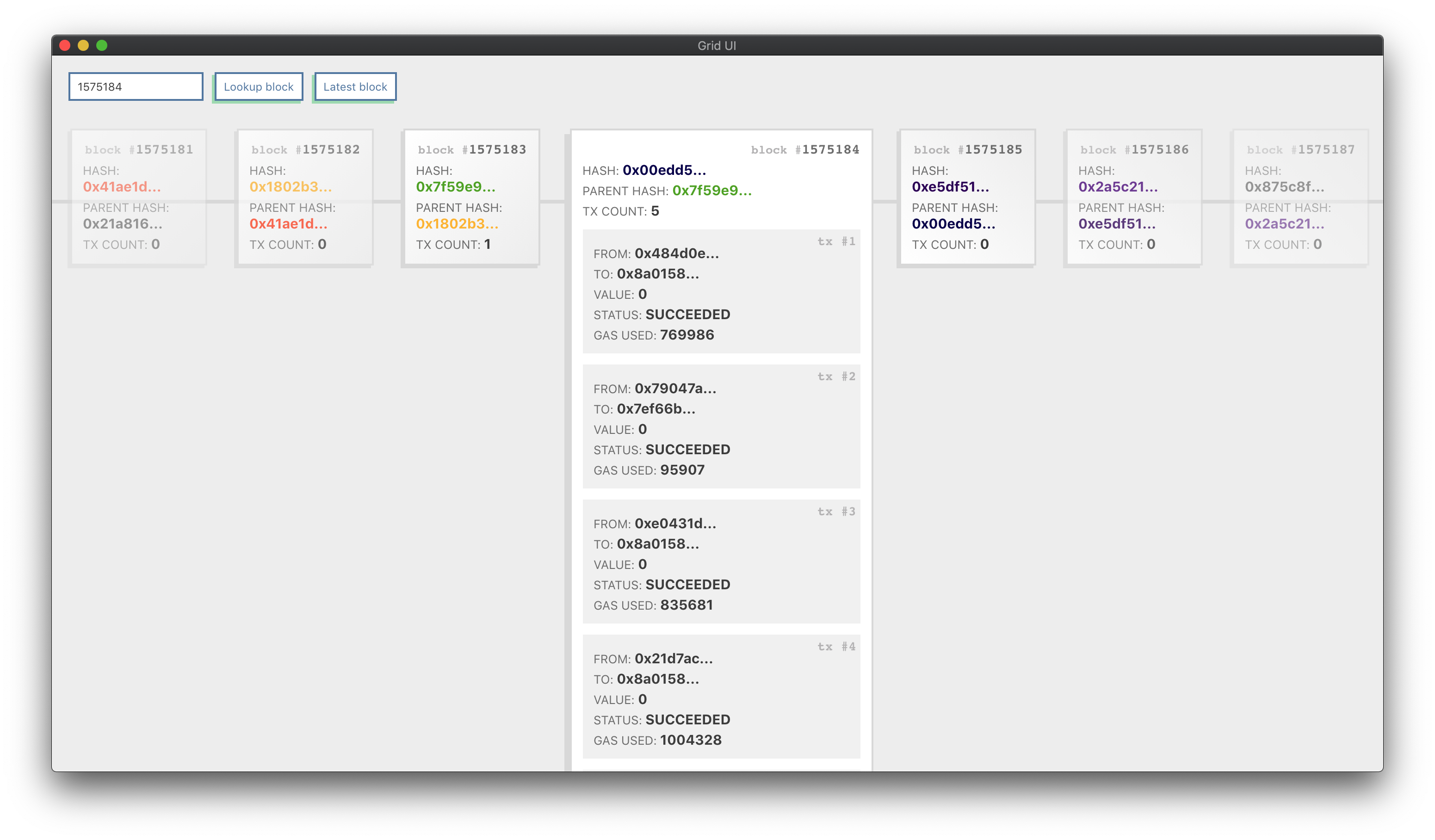
Block Explorer - explore the blockchain visually
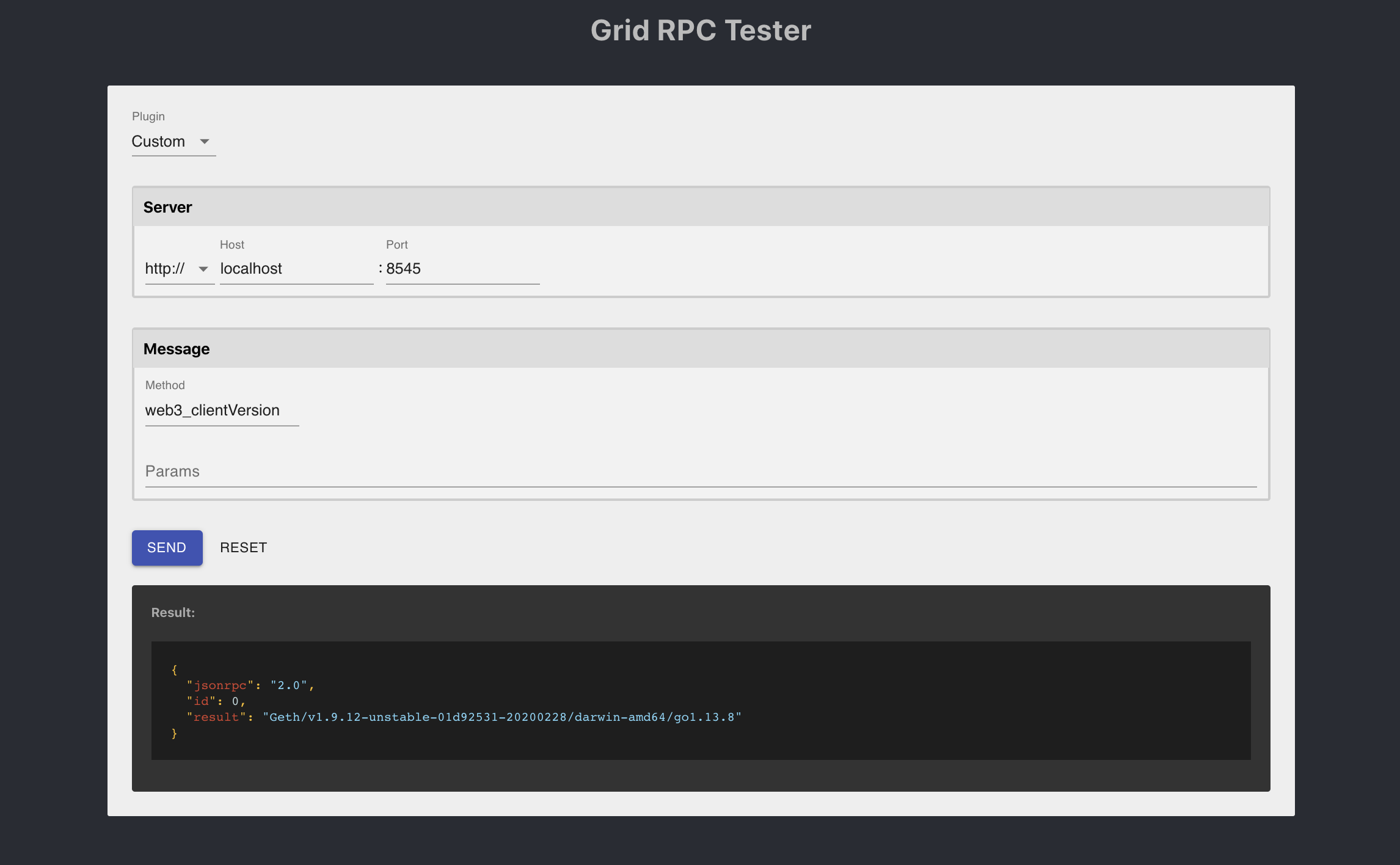
RPC Tester - UI to explore the JSON RPC API of your local node
Ewasm Testnet - Get started with ewasm
REPL - Read–eval–print loop - read a command from stdin, execute with ethers.js on geth. repeat.
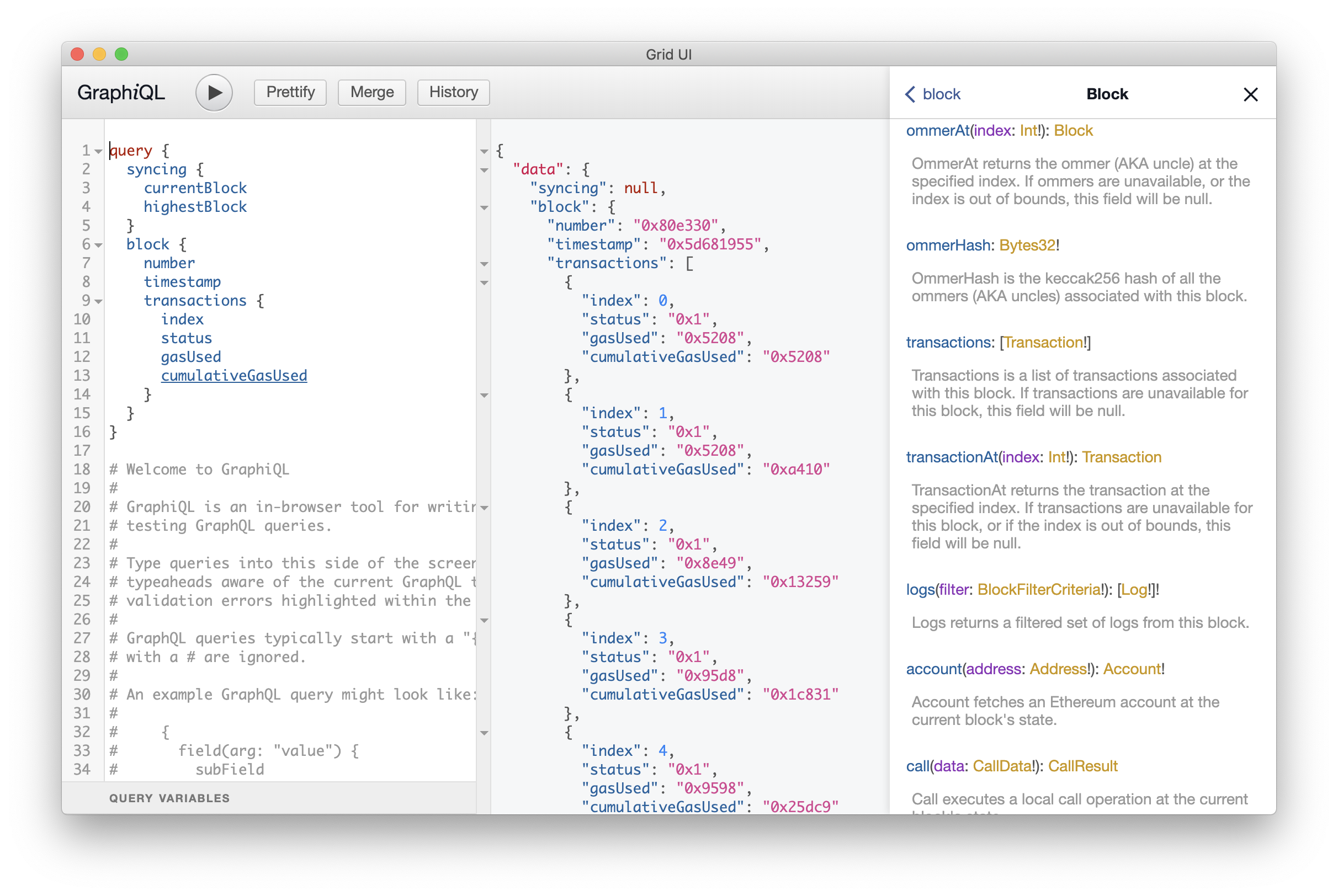
GraphQL Explorer - start Geth's built-in GraphQL UI and query the chain
Hello ZoKrates - proof knowledge of the root of some square number and export a verifier.sol contract
Remix ❤️ Geth - configure a local Geth node to be used with remix.ethereum.org

Hello Grid

Run

grid-core workflow run 0x39830fed4b4b17fcdfa0830f9ab9ed8a1d0c11d9/hello-grid

Description

The obligatory "hello world" for Grid. It just prints "hello grid" to CLI or UI environment - perfect for testing if things are working at all.

Concepts

minimum viable workflow

Eth2 with Prysm

Run

grid-core workflow run 0x39830fed4b4b17fcdfa0830f9ab9ed8a1d0c11d9/eth2-prysm-testnet

Description

This workflow sets up a validator account for the prysm eth2 testnet as described here: https://prylabs.net/participate

The workflow requires a running docker server.

This workflow is WIP.

Concepts

Orchestration of multiple Docker clients and local Geth
- Bonus points: Sharing data between containers and workflow without using fs
Using non-bash docker entrypoints
Using alternative docker registries (Google Cloud)
Prompting user for keys and passwords

Block Explorer

Run

grid-core workflow run 0x39830fed4b4b17fcdfa0830f9ab9ed8a1d0c11d9/block-explorer

Description

This workflow starts a local Geth instance and configures the GraphQL API using the FlagBuilder. It then starts the BlocksApp by @marcgarreau which connects over HTTP to Geth. The Block Explorer can be used to learn more about the blockchain and explore and visualize blocks. More information available in blog post: "Ethereum 101: What’s a Blockchain?"

Screenshots

Concepts:

Geth with GraphQL
Loading a packaged web app with ethpkg and serving it locally
Connecting a UI directly to a workflow binary over HTTP

RPC Tester

Run

grid-core workflow run 0x39830fed4b4b17fcdfa0830f9ab9ed8a1d0c11d9/rpc-tester

Description

This workflow starts a local Geth instance and connects the RPC Tester App by @ryanio to it.

Screenshots

RPC Tester UI

Workflow + Geth logs

Concepts:

Geth with manual/raw flags (no FlagBuilder)
Loading a packaged web app with ethpkg and serving it locally
Connecting a UI directly to RPC
Printing / managing Geth logs + colored output
keepAlive() API

Ewasm Testnet

Run

grid-core workflow run 0x39830fed4b4b17fcdfa0830f9ab9ed8a1d0c11d9/ewasm

Description

This workflow starts the Ewasm testnet in a Docker container, connects ethers.js to it and requests the web3_clientVersion over RPC.

Concepts:

Dockerfile in workflow
- binaries are built using the docker builder pattern
- docker entry point definition
- binary as long running service
FlagBuilder with .docker()

Example output

Grid Version 1.0.3

Grid uses configuration: Projects/workflows/.grid.config.js 

Starting workflow:
======================================================================
Name: ewasm
Version: 1.0.0
Description: This workflow demonstrates how to use Dockerfiles to build binaries such as Ewasm and connect to a container.
======================================================================
Output:
              
INFO : >> hello ewasm
INFO : >> run with config {}
✖ No existing container found for "grid_ewasm"
✔ Created Docker image "grid_ewasm" from Dockerfile
  DOCKER:Step 1/18 : FROM golang:1.13-alpine as builder
  DOCKER:---> 3024b4e742b0
  DOCKER:Step 2/18 : RUN apk update && apk add --no-cache     autoconf build-base binutils cmake make curl file gcc g++ git libgcc libtool linux-headers make musl-dev
  DOCKER:---> Using cache
  DOCKER:---> 84ca854b817d
  DOCKER:Step 3/18 : RUN git clone https://github.com/ewasm/go-ethereum -b ewasm-testnet-milestone1
  DOCKER:---> Using cache
  DOCKER:---> a4178391e40a
  DOCKER:Step 4/18 : RUN cd ./go-ethereum && make geth
  DOCKER:---> Using cache
  DOCKER:---> 81e97751fd10
  DOCKER:Step 5/18 : RUN git clone https://github.com/ewasm/hera
  DOCKER:---> Using cache
  DOCKER:---> 80fe9df70a44
  DOCKER:Step 6/18 : RUN cd hera && git submodule update --init
  DOCKER:---> Using cache
  DOCKER:---> fd4ad6632be1
  DOCKER:Step 7/18 : RUN cd hera && mkdir build
  DOCKER:---> Using cache
  DOCKER:---> 03df92ca9639
  DOCKER:Step 8/18 : WORKDIR /go/hera/build
  DOCKER:---> Using cache
  DOCKER:---> b8375edf4636
  DOCKER:Step 9/18 : RUN cmake .. -DBUILD_SHARED_LIBS=ON
  DOCKER:---> Using cache
  DOCKER:---> 0d0b4333e1ea
  DOCKER:Step 10/18 : RUN cmake --build .
  DOCKER:---> Using cache
  DOCKER:---> 3e9daafe5fdf
  DOCKER:Step 11/18 : FROM alpine:latest
  DOCKER:---> 965ea09ff2eb
  DOCKER:Step 12/18 : RUN apk add --no-cache ca-certificates
  DOCKER:---> Using cache
  DOCKER:---> 188a80acf5d6
  DOCKER:Step 13/18 : COPY --from=builder /go/go-ethereum/build/bin/geth /usr/local/bin/
  DOCKER:---> Using cache
  DOCKER:---> 829626f816df
  DOCKER:Step 14/18 : COPY --from=builder /go/hera/build/src/libhera.so /usr/local/bin/
  DOCKER:---> Using cache
  DOCKER:---> d68908996c8e
  DOCKER:Step 15/18 : WORKDIR /usr/local/bin
  DOCKER:---> Using cache
  DOCKER:---> 6651100b225c
  DOCKER:Step 16/18 : RUN wget https://raw.githubusercontent.com/ewasm/testnet/ewasm-testnet-milestone1/ewasm-testnet-geth-config.json
  DOCKER:---> Using cache
  DOCKER:---> e6eb97e3fc98
  DOCKER:Step 17/18 : RUN geth --datadir /tmp/ewasm-node/4201/ init ewasm-testnet-geth-config.json
  DOCKER:---> Using cache
  DOCKER:---> 40764add28c7
  DOCKER:Step 18/18 : EXPOSE 8545 8546 8547 30303 30303/udp
  DOCKER:---> Using cache
  DOCKER:---> d46779dfd92e
  DOCKER:Successfully built d46779dfd92e
  DOCKER:Successfully tagged grid_ewasm:latest
✔ Created Docker container "grid_ewasm" from Dockerfile
INFO : >> client: Geth/v1.8.17-evmc.6.0.0-1-stable/linux-amd64/go1.13.4
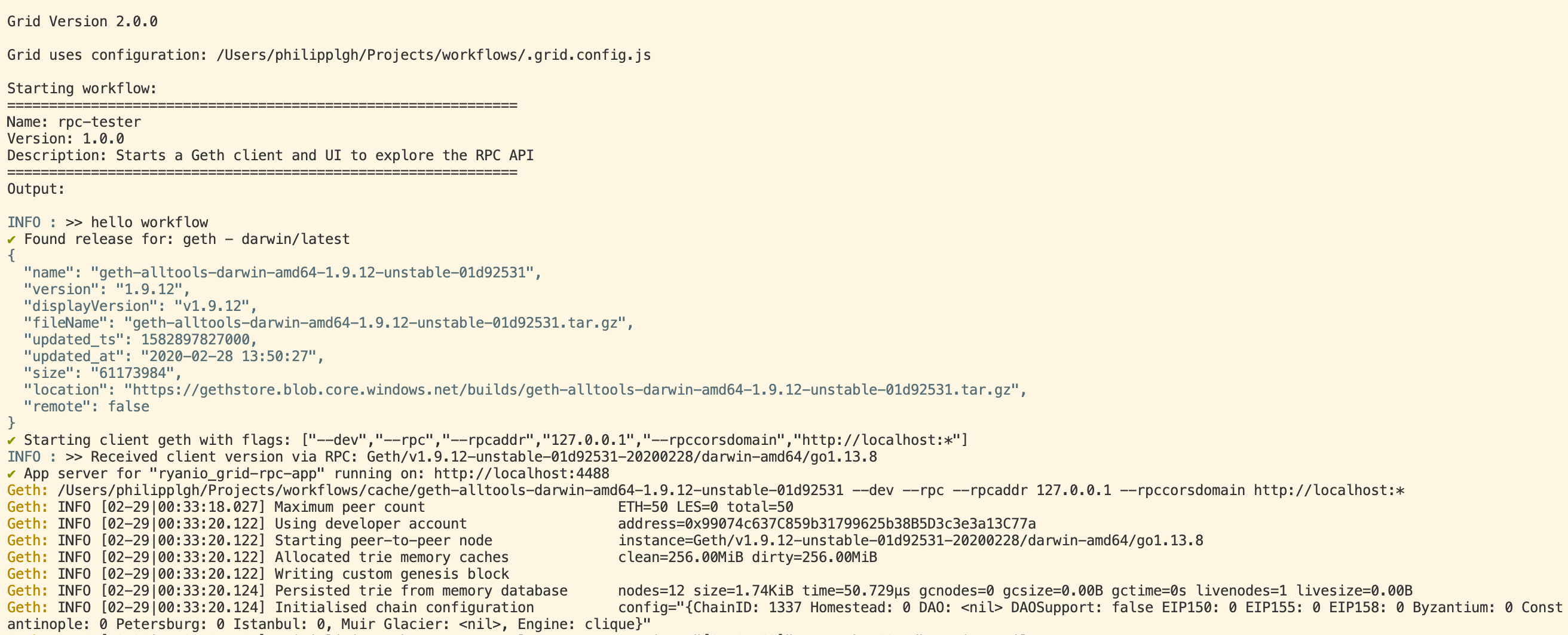
INFO : >> network: { chainId: 66, name: 'unknown' }

REPL: read eval print loop

Run

grid-core workflow run 0x39830fed4b4b17fcdfa0830f9ab9ed8a1d0c11d9/ethers-repl

Description

This workflow starts a <client> instance. client and version are flags that can be passed to the workflow to specify which client. Defaults are geth and latest. It configures the RPC API with the FlagBuilder in a client agnostic way and connects ethers.js to it. Last but not least the workflow enters a loop where it uses Grid's prompt API to ask the user for input and execute it as ethers.js commands. The result is similar to the JSRE REPL Console but with ethers.js and theoretically any client that can open an RPC endpoint.

Concepts

prompt user for input
export run function parameter description
processing of user provided flags: --client=geth

Example Output

Grid Version 2.0.0
Grid uses configuration: Projects/workflows/.grid.config.js 

Starting workflow:
=============================================================
Name: ethers-repl
Version: 1.0.0
Description: This workflow creates Read–eval–print loop (REPL) and executes ethers.js commands on a local Geth instance.
=============================================================
Output:
              
INFO : >> hello repl
INFO : >> run with config { client: 'geth', version: 'latest' }
✔ Found release for: geth - darwin/latest
{
  "name": "geth-alltools-darwin-amd64-1.9.12-unstable-01d92531",
  "version": "1.9.12",
  "displayVersion": "v1.9.12",
  "fileName": "geth-alltools-darwin-amd64-1.9.12-unstable-01d92531.tar.gz",
  "updated_ts": 1582897827000,
  "updated_at": "2020-02-28 13:50:27",
  "size": "61173984",
  "location": "https://gethstore.blob.core.windows.net/builds/geth-alltools-darwin-amd64-1.9.12-unstable-01d92531.tar.gz",
  "remote": false
}
✔ Starting client geth with flags: ["--dev","--rpc","--rpcaddr","127.0.0.1","--rpccorsdomain","localhost:*,127.0.0.1:*"]
INFO : >> Received client version via RPC: Geth/v1.9.12-unstable-01d92531-20200228/darwin-amd64/go1.13.8
INFO : >> ethers.js:  4.0.40
INFO : Type something in this interactive ethers REPL
INFO : Try: ethereum.getNetwork()
> ethereum.getNetwork()
INFO : result: <Promise> =>  { chainId: 1337, name: 'unknown' }
>

GraphQL Explorer

Run

grid-core workflow run 0x39830fed4b4b17fcdfa0830f9ab9ed8a1d0c11d9/graphql-explorer

Description

This workflow configures Geth to start the integrated GraphQL server and opens the UI to write and run queries.

Screenshots

GraphiQL Interface

Concepts

Navigating to local server

Hello ZoKrates

Run

grid-core workflow run 0x39830fed4b4b17fcdfa0830f9ab9ed8a1d0c11d9/hello-zokrates

Description

This workflow runs the official DockerHub hosted ZoKrates container. It moves source code into the running container, executes various commands from the "hello world" tutorial on the ZoKrates binary inside the container and finally exports the verifier.sol.

Concepts

Run DockerHub containers
Execution of bash commands with and without entrypoint
Move files between workflow and container

Example Output

Grid Version 1.0.3

Grid uses configuration: Projects/workflows/.grid.config.js 

Starting workflow:
======================================================================
Name: hello-zokrates
Version: 1.0.0
Description: Runs the ZoKrates 'hello world' and exports the verifier.sol
======================================================================
Output:
              
INFO : >> hello zokrates {}
✔ Found existing Docker container
✔ Docker client ready!
ZoKrates: compile output:
 [
  'Compiling root.zok',
  ',|Compiled program:',
  'def main(_0, _1) -> (1):',
  '(1 * _0) * (1 * _0) == 1 * _4',
  '# _2, _3 = ConditionEq((-1) * _1 + 1 * _4)',
  '((-1) * _1 + 1 * _4) * (1 * _3) == 1 * _2',
  '(1 * ~one + (-1) * _2) * ((-1) * _1 + 1 * _4) == 0',
  '(1 * ~one) * (1 * ~one + (-1) * _2) == 1 * ~out_0',
  ' return ~out_0',
  "Compiled code written to 'out'",
  "Human readable code to 'out.ztf'",
  'Number of constraints: 4'
]
ZoKrates: setup phase output:
 [
  'Performing setup...',
  ',def main(_0, _1) -> (1):',
  '(1 * _0) * (1 * _0) == 1 * _4',
  '# _2, _3 = ConditionEq((-1) * _1 + 1 * _4)',
  '((-1) * _1 + 1 * _4) * (1 * _3) == 1 * _2',
  '(1 * ~one + (-1) * _2) * ((-1) * _1 + 1 * _4) == 0',
  '(1 * ~one) * (1 * ~one + (-1) * _2) == 1 * ~out_0',
  ' return ~out_0',
  'WARNING: You are using the G16 scheme which is subject to malleability. See zokrates.github.io/reference/proving_schemes.html#g16-malleability for implications.',
  ',Has generated 7 points',
  ',Setup completed.'
]
ZoKrates: execute program output:
 [
  '2Computing witness...',
  'def main(_0, _1) -> (1):',
  '(1 * _0) * (1 * _0) == 1 * _4',
  '# _2, _3 = ConditionEq((-1) * _1 + 1 * _4)',
  '((-1) * _1 + 1 * _4) * (1 * _3) == 1 * _2',
  '(1 * ~one + (-1) * _2) * ((-1) * _1 + 1 * _4) == 0',
  '(1 * ~one) * (1 * ~one + (-1) * _2) == 1 * ~out_0',
  ' return ~out_0',
  'Witness: ',
  ',["1"]'
]
ZoKrates: "generate a proof of computation" output:
 [
  'Generating proof...',
  ',WARNING: You are using the G16 scheme which is subject to malleability. See zokrates.github.io/reference/proving_schemes.html#g16-malleability for implications.',
  ',Tgenerate-proof successful: {',
  '        "proof": {',
  '            "a": ["0x2ea377caf7635203e02a1c3e0e48b73cc7bcdab40449275f884a248e2302d598", "0x1ac3d8199aebe63c36d867942bb8a62361973e51390c41d7c27283dbd02076a9"],',
  '            "b": [["0x030dc19cb238db5cf3ef90c463e6d8d5ba06f452dc443e49fdfa2f5e878e46fd", "0x27f7b46b36f968d5f4dab8b8b15f7fa63766325646403aa3a89ce584dde0898f"], ["0x12e5a0601c9906932350d2c1fb34faa270591fe7d5b29a8b399f7622c03cdc9f", "0x0757e81a7a3240939c9ebb724695f5696b9b89c5fd734028bfaf6160de218fbd"]],',
  '            "c": ["0x22557b4a1d67dcc661a1a689c62e1b0200cc847daac959df352d85b03c0049bf", "0x02f47002c238a84d04da2eddb26c62655682f2f141085ef8b3247b324851fc3c"]',
  '        },',
  '        "inputs": ["0x000000000000000000000000000000000000000000000000000000000001bba1", "0x0000000000000000000000000000000000000000000000000000000000000001"]',
  '    }'
]
ZoKrates: "export a solidity verifier" output:
 [ 'Exporting verifier...', ',Finished exporting verifier.' ]
INFO : files: [
  'total 10700',
  ',Adrwxr-xr-x  1 zokrates zokrates     4096 Mar  3 11:19 .',
  'drwxr-xr-x  1 root     root         4096 Feb 25 11:06 ..',
  '-rw-r--r--  1 zokrates zokrates      220 Apr  4  2018 .bash_logout',
  '-rw-r--r--  1 zokrates zokrates     3771 Apr  4  2018 .bashrc',
  '-rw-r--r--  1 zokrates zokrates      807 Feb 25 11:16 .profile',
  'drwxr-xr-x  1 zokrates zokrates     4096 Feb 25 11:16 .zokrates',
  '-rw-r--r--  1 zokrates zokrates      227 Mar  3 11:19 abi.json',
  'drwxr-xr-x 12 zokrates zokrates     4096 Feb 25 11:05 examples',
  '-rw-r--r--  1 zokrates zokrates      727 Mar  3 11:19 out',
  '-rw-r--r--  1 zokrates zokrates      262 Mar  3 11:19 out.ztf',
  '-rw-r--r--  1 zokrates zokrates      816 Mar  3 11:19 proof.json',
  '-rw-r--r--  1 zokrates zokrates     3032 Mar  3 11:19 proving.key',
  '-rw-r--r--  1 root     root          112 Mar  3 11:19 root.zok',
  '-rw-r--r--  1 zokrates zokrates     1504 Mar  3 11:19 verification.key',
  '-rw-r--r--  1 zokrates zokrates    24736 Mar  3 11:19 verifier.sol',
  '-rw-r--r--  1 zokrates zokrates       53 Mar  3 11:19 witness',
  '-rwxr-xr-x  1 zokrates zokrates 10859016 Feb 25 11:16 zokrates'
]
INFO : contract // This file is LGPL3 Licensed
pragma solidity ^0.6.1;

/**
 * @title Elliptic curve operations on twist points for alt_bn128
 * @author Mustafa Al-Bassam (mus@musalbas.com)
 * @dev Homepage: https://github.com/musalbas/solidity-BN256G2
 */

library BN256G2 {
    uint256 internal constant FIELD_MODULUS = 0x30644e72e131a029b85045b68181585d97816a916871ca8d3c208c16d87cfd47;
    uint256 internal constant TWISTBX = 0x2b149d40ceb8aaae81be18991be06ac3b5b4c5e559dbefa33267e6dc24a138e5;
    uint256 internal constant TWISTBY = 0x9713b03af0fed4cd2cafadeed8fdf4a74fa084e52d1852e4a2bd0685c315d2;
    uint internal constant PTXX = 0;
    uint internal constant PTXY = 1;
    uint internal constant PTYX = 2;
    uint internal constant PTYY = 3;
    uint internal constant PTZX = 4;
    uint internal constant PTZY = 5;

    /**
     * @notice Add two twist points
     * @param pt1xx Coefficient 1 of x on point 1
     * @param pt1xy Coefficient 2 of x on point 1
     * @param pt1yx Coefficient 1 of y on point 1
     * @param pt1yy Coefficient 2 of y on point 1
     * @param pt2xx Coefficient 1 of x on point 2
     * @param pt2xy Coefficient 2 of x on point 2
     * @param pt2yx Coefficient 1 of y on point 2
     * @param pt2yy Coefficient 2 of y on point 2
     * @return (pt3xx, pt3xy, pt3yx, pt3yy)
     */
    function ECTwistAdd(
        uint256 pt1xx, uint256 pt1xy,
        uint256 pt1yx, uint256 pt1yy,
        uint256 pt2xx, uint256 pt2xy,
        uint256 pt2yx, uint256 pt2yy
    ) public view returns (
        uint256, uint256,
        uint256, uint256
    ) {
        if (
            pt1xx == 0 && pt1xy == 0 &&
            pt1yx == 0 && pt1yy == 0
        ) {
            if (!(
                pt2xx == 0 && pt2xy == 0 &&
                pt2yx == 0 && pt2yy == 0
            )) {
                assert(_isOnCurve(
                    pt2xx, pt2xy,
                    pt2yx, pt2yy
                ));
            }
            return (
                pt2xx, pt2xy,
                pt2yx, pt2yy
            );
        } else if (
            pt2xx == 0 && pt2xy == 0 &&
            pt2yx == 0 && pt2yy == 0
        ) {
            assert(_isOnCurve(
                pt1xx, pt1xy,
                pt1yx, pt1yy
            ));
            return (
                pt1xx, pt1xy,
                pt1yx, pt1yy
            );
        }

        assert(_isOnCurve(
            pt1xx, pt1xy,
            pt1yx, pt1yy
        ));
        assert(_isOnCurve(
            pt2xx, pt2xy,
            pt2yx, pt2yy
        ));

        uint256[6] memory pt3 = _ECTwistAddJacobian(
            pt1xx, pt1xy,
            pt1yx, pt1yy,
            1,     0,
            pt2xx, pt2xy,
            pt2yx, pt2yy,
            1,     0
        );

        return _fromJacobian(
            pt3[PTXX], pt3[PTXY],
            pt3[PTYX], pt3[PTYY],
            pt3[PTZX], pt3[PTZY]
        );
    }

    /**
     * @notice Multiply a twist point by a scalar
     * @param s     Scalar to multiply by
     * @param pt1xx Coefficient 1 of x
     * @param pt1xy Coefficient 2 of x
     * @param pt1yx Coefficient 1 of y
     * @param pt1yy Coefficient 2 of y
     * @return (pt2xx, pt2xy, pt2yx, pt2yy)
     */
    function ECTwistMul(
        uint256 s,
        uint256 pt1xx, uint256 pt1xy,
        uint256 pt1yx, uint256 pt1yy
    ) public view returns (
        uint256, uint256,
        uint256, uint256
    ) {
        uint256 pt1zx = 1;
        if (
            pt1xx == 0 && pt1xy == 0 &&
            pt1yx == 0 && pt1yy == 0
        ) {
            pt1xx = 1;
            pt1yx = 1;
            pt1zx = 0;
        } else {
            assert(_isOnCurve(
                pt1xx, pt1xy,
                pt1yx, pt1yy
            ));
        }

        uint256[6] memory pt2 = _ECTwistMulJacobian(
            s,
            pt1xx, pt1xy,
            pt1yx, pt1yy,
            pt1zx, 0
        );

        return _fromJacobian(
            pt2[PTXX], pt2[PTXY],
            pt2[PTYX], pt2[PTYY],
            pt2[PTZX], pt2[PTZY]
        );
    }

    /**
     * @notice Get the field modulus
     * @return The field modulus
     */
    function GetFieldModulus() public pure returns (uint256) {
        return FIELD_MODULUS;
    }

    function submod(uint256 a, uint256 b, uint256 n) internal pure returns (uint256) {
        return addmod(a, n - b, n);
    }

    function _FQ2Mul(
        uint256 xx, uint256 xy,
        uint256 yx, uint256 yy
    ) internal pure returns (uint256, uint256) {
        return (
            submod(mulmod(xx, yx, FIELD_MODULUS), mulmod(xy, yy, FIELD_MODULUS), FIELD_MODULUS),
            addmod(mulmod(xx, yy, FIELD_MODULUS), mulmod(xy, yx, FIELD_MODULUS), FIELD_MODULUS)
        );
    }

    function _FQ2Muc(
        uint256 xx, uint256 xy,
        uint256 c
    ) internal pure returns (uint256, uint256) {
        return (
            mulmod(xx, c, FIELD_MODULUS),
            mulmod(xy, c, FIELD_MODULUS)
        );
    }

    function _FQ2Add(
        uint256 xx, uint256 xy,
        uint256 yx, uint256 yy
    ) internal pure returns (uint256, uint256) {
        return (
            addmod(xx, yx, FIELD_MODULUS),
            addmod(xy, yy, FIELD_MODULUS)
        );
    }

    function _FQ2Sub(
        uint256 xx, uint256 xy,
        uint256 yx, uint256 yy
    ) internal pure returns (uint256 rx, uint256 ry) {
        return (
            submod(xx, yx, FIELD_MODULUS),
            submod(xy, yy, FIELD_MODULUS)
        );
    }

    function _FQ2Div(
        uint256 xx, uint256 xy,
        uint256 yx, uint256 yy
    ) internal view returns (uint256, uint256) {
        (yx, yy) = _FQ2Inv(yx, yy);
        return _FQ2Mul(xx, xy, yx, yy);
    }

    function _FQ2Inv(uint256 x, uint256 y) internal view returns (uint256, uint256) {
        uint256 inv = _modInv(addmod(mulmod(y, y, FIELD_MODULUS), mulmod(x, x, FIELD_MODULUS), FIELD_MODULUS), FIELD_MODULUS);
        return (
            mulmod(x, inv, FIELD_MODULUS),
            FIELD_MODULUS - mulmod(y, inv, FIELD_MODULUS)
        );
    }

    function _isOnCurve(
        uint256 xx, uint256 xy,
        uint256 yx, uint256 yy
    ) internal pure returns (bool) {
        uint256 yyx;
        uint256 yyy;
        uint256 xxxx;
        uint256 xxxy;
        (yyx, yyy) = _FQ2Mul(yx, yy, yx, yy);
        (xxxx, xxxy) = _FQ2Mul(xx, xy, xx, xy);
        (xxxx, xxxy) = _FQ2Mul(xxxx, xxxy, xx, xy);
        (yyx, yyy) = _FQ2Sub(yyx, yyy, xxxx, xxxy);
        (yyx, yyy) = _FQ2Sub(yyx, yyy, TWISTBX, TWISTBY);
        return yyx == 0 && yyy == 0;
    }

    function _modInv(uint256 a, uint256 n) internal view returns (uint256 result) {
        bool success;
        assembly {
            let freemem := mload(0x40)
            mstore(freemem, 0x20)
            mstore(add(freemem,0x20), 0x20)
            mstore(add(freemem,0x40), 0x20)
            mstore(add(freemem,0x60), a)
            mstore(add(freemem,0x80), sub(n, 2))
            mstore(add(freemem,0xA0), n)
            success := staticcall(sub(gas(), 2000), 5, freemem, 0xC0, freemem, 0x20)
            result := mload(freemem)
        }
        require(success);
    }

    function _fromJacobian(
        uint256 pt1xx, uint256 pt1xy,
        uint256 pt1yx, uint256 pt1yy,
        uint256 pt1zx, uint256 pt1zy
    ) internal view returns (
        uint256 pt2xx, uint256 pt2xy,
        uint256 pt2yx, uint256 pt2yy
    ) {
        uint256 invzx;
        uint256 invzy;
        (invzx, invzy) = _FQ2Inv(pt1zx, pt1zy);
        (pt2xx, pt2xy) = _FQ2Mul(pt1xx, pt1xy, invzx, invzy);
        (pt2yx, pt2yy) = _FQ2Mul(pt1yx, pt1yy, invzx, invzy);
    }

    function _ECTwistAddJacobian(
        uint256 pt1xx, uint256 pt1xy,
        uint256 pt1yx, uint256 pt1yy,
        uint256 pt1zx, uint256 pt1zy,
        uint256 pt2xx, uint256 pt2xy,
        uint256 pt2yx, uint256 pt2yy,
        uint256 pt2zx, uint256 pt2zy) internal pure returns (uint256[6] memory pt3) {
            if (pt1zx == 0 && pt1zy == 0) {
                (
                    pt3[PTXX], pt3[PTXY],
                    pt3[PTYX], pt3[PTYY],
                    pt3[PTZX], pt3[PTZY]
                ) = (
                    pt2xx, pt2xy,
                    pt2yx, pt2yy,
                    pt2zx, pt2zy
                );
                return pt3;
            } else if (pt2zx == 0 && pt2zy == 0) {
                (
                    pt3[PTXX], pt3[PTXY],
                    pt3[PTYX], pt3[PTYY],
                    pt3[PTZX], pt3[PTZY]
                ) = (
                    pt1xx, pt1xy,
                    pt1yx, pt1yy,
                    pt1zx, pt1zy
                );
                return pt3;
            }

            (pt2yx,     pt2yy)     = _FQ2Mul(pt2yx, pt2yy, pt1zx, pt1zy); // U1 = y2 * z1
            (pt3[PTYX], pt3[PTYY]) = _FQ2Mul(pt1yx, pt1yy, pt2zx, pt2zy); // U2 = y1 * z2
            (pt2xx,     pt2xy)     = _FQ2Mul(pt2xx, pt2xy, pt1zx, pt1zy); // V1 = x2 * z1
            (pt3[PTZX], pt3[PTZY]) = _FQ2Mul(pt1xx, pt1xy, pt2zx, pt2zy); // V2 = x1 * z2

            if (pt2xx == pt3[PTZX] && pt2xy == pt3[PTZY]) {
                if (pt2yx == pt3[PTYX] && pt2yy == pt3[PTYY]) {
                    (
                        pt3[PTXX], pt3[PTXY],
                        pt3[PTYX], pt3[PTYY],
                        pt3[PTZX], pt3[PTZY]
                    ) = _ECTwistDoubleJacobian(pt1xx, pt1xy, pt1yx, pt1yy, pt1zx, pt1zy);
                    return pt3;
                }
                (
                    pt3[PTXX], pt3[PTXY],
                    pt3[PTYX], pt3[PTYY],
                    pt3[PTZX], pt3[PTZY]
                ) = (
                    1, 0,
                    1, 0,
                    0, 0
                );
                return pt3;
            }

            (pt2zx,     pt2zy)     = _FQ2Mul(pt1zx, pt1zy, pt2zx,     pt2zy);     // W = z1 * z2
            (pt1xx,     pt1xy)     = _FQ2Sub(pt2yx, pt2yy, pt3[PTYX], pt3[PTYY]); // U = U1 - U2
            (pt1yx,     pt1yy)     = _FQ2Sub(pt2xx, pt2xy, pt3[PTZX], pt3[PTZY]); // V = V1 - V2
            (pt1zx,     pt1zy)     = _FQ2Mul(pt1yx, pt1yy, pt1yx,     pt1yy);     // V_squared = V * V
            (pt2yx,     pt2yy)     = _FQ2Mul(pt1zx, pt1zy, pt3[PTZX], pt3[PTZY]); // V_squared_times_V2 = V_squared * V2
            (pt1zx,     pt1zy)     = _FQ2Mul(pt1zx, pt1zy, pt1yx,     pt1yy);     // V_cubed = V * V_squared
            (pt3[PTZX], pt3[PTZY]) = _FQ2Mul(pt1zx, pt1zy, pt2zx,     pt2zy);     // newz = V_cubed * W
            (pt2xx,     pt2xy)     = _FQ2Mul(pt1xx, pt1xy, pt1xx,     pt1xy);     // U * U
            (pt2xx,     pt2xy)     = _FQ2Mul(pt2xx, pt2xy, pt2zx,     pt2zy);     // U * U * W
            (pt2xx,     pt2xy)     = _FQ2Sub(pt2xx, pt2xy, pt1zx,     pt1zy);     // U * U * W - V_cubed
            (pt2zx,     pt2zy)     = _FQ2Muc(pt2yx, pt2yy, 2);                    // 2 * V_squared_times_V2
            (pt2xx,     pt2xy)     = _FQ2Sub(pt2xx, pt2xy, pt2zx,     pt2zy);     // A = U * U * W - V_cubed - 2 * V_squared_times_V2
            (pt3[PTXX], pt3[PTXY]) = _FQ2Mul(pt1yx, pt1yy, pt2xx,     pt2xy);     // newx = V * A
            (pt1yx,     pt1yy)     = _FQ2Sub(pt2yx, pt2yy, pt2xx,     pt2xy);     // V_squared_times_V2 - A
            (pt1yx,     pt1yy)     = _FQ2Mul(pt1xx, pt1xy, pt1yx,     pt1yy);     // U * (V_squared_times_V2 - A)
            (pt1xx,     pt1xy)     = _FQ2Mul(pt1zx, pt1zy, pt3[PTYX], pt3[PTYY]); // V_cubed * U2
            (pt3[PTYX], pt3[PTYY]) = _FQ2Sub(pt1yx, pt1yy, pt1xx,     pt1xy);     // newy = U * (V_squared_times_V2 - A) - V_cubed * U2
    }

    function _ECTwistDoubleJacobian(
        uint256 pt1xx, uint256 pt1xy,
        uint256 pt1yx, uint256 pt1yy,
        uint256 pt1zx, uint256 pt1zy
    ) internal pure returns (
        uint256 pt2xx, uint256 pt2xy,
        uint256 pt2yx, uint256 pt2yy,
        uint256 pt2zx, uint256 pt2zy
    ) {
        (pt2xx, pt2xy) = _FQ2Muc(pt1xx, pt1xy, 3);            // 3 * x
        (pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt1xx, pt1xy); // W = 3 * x * x
        (pt1zx, pt1zy) = _FQ2Mul(pt1yx, pt1yy, pt1zx, pt1zy); // S = y * z
        (pt2yx, pt2yy) = _FQ2Mul(pt1xx, pt1xy, pt1yx, pt1yy); // x * y
        (pt2yx, pt2yy) = _FQ2Mul(pt2yx, pt2yy, pt1zx, pt1zy); // B = x * y * S
        (pt1xx, pt1xy) = _FQ2Mul(pt2xx, pt2xy, pt2xx, pt2xy); // W * W
        (pt2zx, pt2zy) = _FQ2Muc(pt2yx, pt2yy, 8);            // 8 * B
        (pt1xx, pt1xy) = _FQ2Sub(pt1xx, pt1xy, pt2zx, pt2zy); // H = W * W - 8 * B
        (pt2zx, pt2zy) = _FQ2Mul(pt1zx, pt1zy, pt1zx, pt1zy); // S_squared = S * S
        (pt2yx, pt2yy) = _FQ2Muc(pt2yx, pt2yy, 4);            // 4 * B
        (pt2yx, pt2yy) = _FQ2Sub(pt2yx, pt2yy, pt1xx, pt1xy); // 4 * B - H
        (pt2yx, pt2yy) = _FQ2Mul(pt2yx, pt2yy, pt2xx, pt2xy); // W * (4 * B - H)
        (pt2xx, pt2xy) = _FQ2Muc(pt1yx, pt1yy, 8);            // 8 * y
        (pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt1yx, pt1yy); // 8 * y * y
        (pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt2zx, pt2zy); // 8 * y * y * S_squared
        (pt2yx, pt2yy) = _FQ2Sub(pt2yx, pt2yy, pt2xx, pt2xy); // newy = W * (4 * B - H) - 8 * y * y * S_squared
        (pt2xx, pt2xy) = _FQ2Muc(pt1xx, pt1xy, 2);            // 2 * H
        (pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt1zx, pt1zy); // newx = 2 * H * S
        (pt2zx, pt2zy) = _FQ2Mul(pt1zx, pt1zy, pt2zx, pt2zy); // S * S_squared
        (pt2zx, pt2zy) = _FQ2Muc(pt2zx, pt2zy, 8);            // newz = 8 * S * S_squared
    }

    function _ECTwistMulJacobian(
        uint256 d,
        uint256 pt1xx, uint256 pt1xy,
        uint256 pt1yx, uint256 pt1yy,
        uint256 pt1zx, uint256 pt1zy
    ) internal pure returns (uint256[6] memory pt2) {
        while (d != 0) {
            if ((d & 1) != 0) {
                pt2 = _ECTwistAddJacobian(
                    pt2[PTXX], pt2[PTXY],
                    pt2[PTYX], pt2[PTYY],
                    pt2[PTZX], pt2[PTZY],
                    pt1xx, pt1xy,
                    pt1yx, pt1yy,
                    pt1zx, pt1zy);
            }
            (
                pt1xx, pt1xy,
                pt1yx, pt1yy,
                pt1zx, pt1zy
            ) = _ECTwistDoubleJacobian(
                pt1xx, pt1xy,
                pt1yx, pt1yy,
                pt1zx, pt1zy
            );

            d = d / 2;
        }
    }
}
// This file is MIT Licensed.
//
// Copyright 2017 Christian Reitwiessner
// Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
// The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
// THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
pragma solidity ^0.6.1;
library Pairing {
    struct G1Point {
        uint X;
        uint Y;
    }
    // Encoding of field elements is: X[0] * z + X[1]
    struct G2Point {
        uint[2] X;
        uint[2] Y;
    }
    /// @return the generator of G1
    function P1() pure internal returns (G1Point memory) {
        return G1Point(1, 2);
    }
    /// @return the generator of G2
    function P2() pure internal returns (G2Point memory) {
        return G2Point(
            [11559732032986387107991004021392285783925812861821192530917403151452391805634,
             10857046999023057135944570762232829481370756359578518086990519993285655852781],
            [4082367875863433681332203403145435568316851327593401208105741076214120093531,
             8495653923123431417604973247489272438418190587263600148770280649306958101930]
        );
    }
    /// @return the negation of p, i.e. p.addition(p.negate()) should be zero.
    function negate(G1Point memory p) pure internal returns (G1Point memory) {
        // The prime q in the base field F_q for G1
        uint q = 21888242871839275222246405745257275088696311157297823662689037894645226208583;
        if (p.X == 0 && p.Y == 0)
            return G1Point(0, 0);
        return G1Point(p.X, q - (p.Y % q));
    }
    /// @return r the sum of two points of G1
    function addition(G1Point memory p1, G1Point memory p2) internal returns (G1Point memory r) {
        uint[4] memory input;
        input[0] = p1.X;
        input[1] = p1.Y;
        input[2] = p2.X;
        input[3] = p2.Y;
        bool success;
        assembly {
            success := call(sub(gas(), 2000), 6, 0, input, 0xc0, r, 0x60)
            // Use "invalid" to make gas estimation work
            switch success case 0 { invalid() }
        }
        require(success);
    }
    /// @return r the sum of two points of G2
    function addition(G2Point memory p1, G2Point memory p2) internal returns (G2Point memory r) {
        (r.X[1], r.X[0], r.Y[1], r.Y[0]) = BN256G2.ECTwistAdd(p1.X[1],p1.X[0],p1.Y[1],p1.Y[0],p2.X[1],p2.X[0],p2.Y[1],p2.Y[0]);
    }
    /// @return r the product of a point on G1 and a scalar, i.e.
    /// p == p.scalar_mul(1) and p.addition(p) == p.scalar_mul(2) for all points p.
    function scalar_mul(G1Point memory p, uint s) internal returns (G1Point memory r) {
        uint[3] memory input;
        input[0] = p.X;
        input[1] = p.Y;
        input[2] = s;
        bool success;
        assembly {
            success := call(sub(gas(), 2000), 7, 0, input, 0x80, r, 0x60)
            // Use "invalid" to make gas estimation work
            switch success case 0 { invalid() }
        }
        require (success);
    }
    /// @return the result of computing the pairing check
    /// e(p1[0], p2[0]) *  .... * e(p1[n], p2[n]) == 1
    /// For example pairing([P1(), P1().negate()], [P2(), P2()]) should
    /// return true.
    function pairing(G1Point[] memory p1, G2Point[] memory p2) internal returns (bool) {
        require(p1.length == p2.length);
        uint elements = p1.length;
        uint inputSize = elements * 6;
        uint[] memory input = new uint[](inputSize);
        for (uint i = 0; i < elements; i++)
        {
            input[i * 6 + 0] = p1[i].X;
            input[i * 6 + 1] = p1[i].Y;
            input[i * 6 + 2] = p2[i].X[0];
            input[i * 6 + 3] = p2[i].X[1];
            input[i * 6 + 4] = p2[i].Y[0];
            input[i * 6 + 5] = p2[i].Y[1];
        }
        uint[1] memory out;
        bool success;
        assembly {
            success := call(sub(gas(), 2000), 8, 0, add(input, 0x20), mul(inputSize, 0x20), out, 0x20)
            // Use "invalid" to make gas estimation work
            switch success case 0 { invalid() }
        }
        require(success);
        return out[0] != 0;
    }
    /// Convenience method for a pairing check for two pairs.
    function pairingProd2(G1Point memory a1, G2Point memory a2, G1Point memory b1, G2Point memory b2) internal returns (bool) {
        G1Point[] memory p1 = new G1Point[](2);
        G2Point[] memory p2 = new G2Point[](2);
        p1[0] = a1;
        p1[1] = b1;
        p2[0] = a2;
        p2[1] = b2;
        return pairing(p1, p2);
    }
    /// Convenience method for a pairing check for three pairs.
    function pairingProd3(
            G1Point memory a1, G2Point memory a2,
            G1Point memory b1, G2Point memory b2,
            G1Point memory c1, G2Point memory c2
    ) internal returns (bool) {
        G1Point[] memory p1 = new G1Point[](3);
        G2Point[] memory p2 = new G2Point[](3);
        p1[0] = a1;
        p1[1] = b1;
        p1[2] = c1;
        p2[0] = a2;
        p2[1] = b2;
        p2[2] = c2;
        return pairing(p1, p2);
    }
    /// Convenience method for a pairing check for four pairs.
    function pairingProd4(
            G1Point memory a1, G2Point memory a2,
            G1Point memory b1, G2Point memory b2,
            G1Point memory c1, G2Point memory c2,
            G1Point memory d1, G2Point memory d2
    ) internal returns (bool) {
        G1Point[] memory p1 = new G1Point[](4);
        G2Point[] memory p2 = new G2Point[](4);
        p1[0] = a1;
        p1[1] = b1;
        p1[2] = c1;
        p1[3] = d1;
        p2[0] = a2;
        p2[1] = b2;
        p2[2] = c2;
        p2[3] = d2;
        return pairing(p1, p2);
    }
}

contract Verifier {
    using Pairing for *;
    struct VerifyingKey {
        Pairing.G1Point a;
        Pairing.G2Point b;
        Pairing.G2Point gamma;
        Pairing.G2Point delta;
        Pairing.G1Point[] gamma_abc;
    }
    struct Proof {
        Pairing.G1Point a;
        Pairing.G2Point b;
        Pairing.G1Point c;
    }
    function verifyingKey() pure internal returns (VerifyingKey memory vk) {
        vk.a = Pairing.G1Point(uint256(0x1936c240636390dc823e3a728e94b208eb53c6756d81da57ec3425e05d43ac10), uint256(0x2d70ff78e8216bf29d58923a686d9738278b8ce2fd822e197c85b09286d15566));
        vk.b = Pairing.G2Point([uint256(0x2b4daf047abe2e7f0b311118c1b963b63695dc0d769cea78849604434de055bf), uint256(0x29c13ecb6f33dbc4b3b8a02e2e255511ce4c26a8a2f299efcc94caf2de4fce00)], [uint256(0x1da9020008df7f549751f8a251af3b2dc4a2ad3e0870de54acaedd9fc1b47e17), uint256(0x25ea0d7e2b29de431b86a943db30dbf4d98f68df9ca8a9628d14d1591e817d90)]);
        vk.gamma = Pairing.G2Point([uint256(0x011016e22ae045444f50fb80f246ec486c7e02af09132cd38c4fcf484983e4f2), uint256(0x00e83c788c2878d1d5eba3ed49b0d81e4c0487dedc3e4d1c2baab5833785b62f)], [uint256(0x05eb89e741ed5b5d611cebf92d1ed02cd6f3311089f0d400df7d9ced5a48fd41), uint256(0x132a90a3b0d369ccd66e2a5ba04a935e44d8ad5dca93a76bba592a578130a911)]);
        vk.delta = Pairing.G2Point([uint256(0x065f6a3323a2abffd621fc263f348eb914904b68d5897729ae34a6b9d33f0852), uint256(0x0c3b60f59d3bd50328a04c0ff6d979199685d0526f89f6ac29d6174ce24707a2)], [uint256(0x26e7ebce2b44efef6b6315938e33f0a8ecc82dbad635c9efa681ed85bbb59982), uint256(0x12e0f3721230a0f38f6c9913048d5230fd2615ef3ff7f6ee4b20dfe0bdea1a86)]);
        vk.gamma_abc = new Pairing.G1Point[](3);
        vk.gamma_abc[0] = Pairing.G1Point(uint256(0x1ef8d5d70234aa3e3d8fc4e3f1ca01c703182580b581106798f05b35fd5082c0), uint256(0x2e468046d4ae35138e2032224925d5389712e5ca5e68f4d9c1e1858e7d65602d));
        vk.gamma_abc[1] = Pairing.G1Point(uint256(0x0cefae0e3fa6aa25a4485ab7b21d32794d3431a4e4a5ca82ea427b831534c2c9), uint256(0x23e3d2035b70884e547638b111870f5957f58ad8068f7a21470164ad361e1e88));
        vk.gamma_abc[2] = Pairing.G1Point(uint256(0x030ffe78ec3de150e8688db619bde78e21e894754e6be5ed83742677628b24bc), uint256(0x053392f88cfa9092dfbc0bd199d8159e56207779473c24fc601eff91bcd345ca));
    }
    function verify(uint[] memory input, Proof memory proof) internal returns (uint) {
        uint256 snark_scalar_field = 21888242871839275222246405745257275088548364400416034343698204186575808495617;
        VerifyingKey memory vk = verifyingKey();
        require(input.length + 1 == vk.gamma_abc.length);
        // Compute the linear combination vk_x
        Pairing.G1Point memory vk_x = Pairing.G1Point(0, 0);
        for (uint i = 0; i < input.length; i++) {
            require(input[i] < snark_scalar_field);
            vk_x = Pairing.addition(vk_x, Pairing.scalar_mul(vk.gamma_abc[i + 1], input[i]));
        }
        vk_x = Pairing.addition(vk_x, vk.gamma_abc[0]);
        if(!Pairing.pairingProd4(
             proof.a, proof.b,
             Pairing.negate(vk_x), vk.gamma,
             Pairing.negate(proof.c), vk.delta,
             Pairing.negate(vk.a), vk.b)) return 1;
        return 0;
    }
    event Verified(string s);
    function verifyTx(
            uint[2] memory a,
            uint[2][2] memory b,
            uint[2] memory c,
            uint[2] memory input
        ) public returns (bool r) {
        Proof memory proof;
        proof.a = Pairing.G1Point(a[0], a[1]);
        proof.b = Pairing.G2Point([b[0][0], b[0][1]], [b[1][0], b[1][1]]);
        proof.c = Pairing.G1Point(c[0], c[1]);
        uint[] memory inputValues = new uint[](input.length);
        for(uint i = 0; i < input.length; i++){
            inputValues[i] = input[i];
        }
        if (verify(inputValues, proof) == 0) {
            emit Verified("Transaction successfully verified.");
            return true;
        } else {
            return false;
        }
    }
}

======================================================================

Remix with Geth

Run

Description

Configures downloads, configures and starts a local Geth instance so that it can be used with the hosted remix.ethereum.org IDE.

PhilippLgh/Grid-Workflows

Grid Workflows

Examples

Hello Grid

Run

Description

Concepts

Eth2 with Prysm

Run

Description

Concepts

Block Explorer

Run

Description

Screenshots

Concepts:

RPC Tester

Run

Description

Screenshots

Concepts:

Ewasm Testnet

Run

Description

Concepts:

Example output

REPL: read eval print loop

Run

Description

Concepts

Example Output

GraphQL Explorer

Run

Description

Screenshots

Concepts

Hello ZoKrates

Run

Description

Concepts

Example Output

Remix with Geth

Run

Description

Concepts