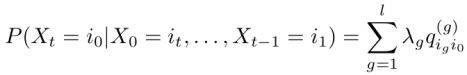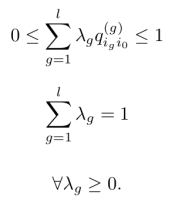pip install mtdlearn
The Generalized Mixture Transition Distribution (MTDg) model was proposed in 1985 by Raftery[1]. It aimed to approximate higher order Markov Chains, but can be used as a standalone model.
Where lambdas are lag parameters and Qg = [qigi0(g)] is a m x m transition matrix representing relationship between g lag and the present state.
To parameters have to meet following constraints to produce probabilities:
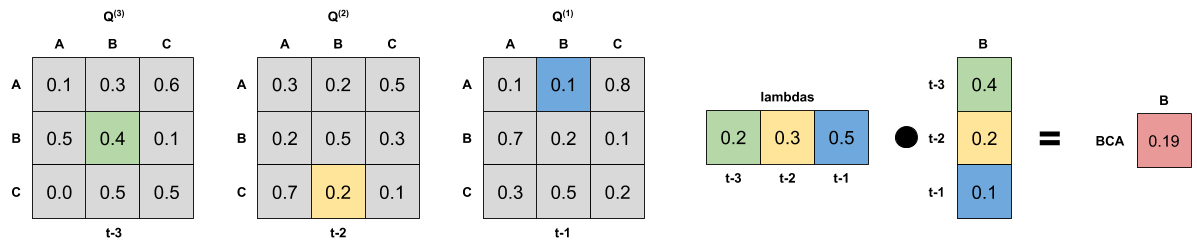
The model can be easier understood as weighted probabilities (by lambdas) of Qg matrices. The example below shows how to calculate a probability of transition B->C->A->B from an order 3 MTDg model:
The number independent parameters of the MTDg model equals (ml - m + 1)(l - 1) and for Markov Chain ml(m-1). You can find a comparison of the number of parameters below.
| States | Order | Markov Chain | MTDg[1] |
|---|---|---|---|
| 2 | 1 | 2 | 2 |
| 2 | 2 | 4 | 3 |
| 2 | 3 | 8 | 4 |
| 2 | 4 | 16 | 5 |
| 3 | 1 | 6 | 6 |
| 3 | 2 | 18 | 10 |
| 3 | 3 | 54 | 14 |
| 3 | 4 | 162 | 18 |
| 5 | 1 | 20 | 20 |
| 5 | 2 | 100 | 36 |
| 5 | 3 | 500 | 52 |
| 5 | 4 | 2500 | 68 |
| 10 | 1 | 90 | 90 |
| 10 | 2 | 900 | 171 |
| 10 | 3 | 9000 | 252 |
| 10 | 4 | 90000 | 333 |
from mtdlearn.mtd import MTD
from mtdlearn.preprocessing import PathEncoder
from mtdlearn.datasets import ChainGenerator
## Generate data
cg = ChainGenerator(('A', 'B', 'C'), 3, min_len=4, max_len=5)
x, y = cg.generate_data(1000)
## Encode paths
pe = PathEncoder(3)
pe.fit(x, y)
x_tr3, y_tr3 = pe.transform(x, y)
## Fitting model
model = MTD(order=3)
model.fit(x_tr3, y_tr3)
For more usage examples please refer to examples section.
GitHub Issues for bug reports, feature requests and questions.
Any contribution is welcome! Please follow this branching model.
MIT License (see LICENSE).
- Introduction to MTDg model The Mixture Transition Distribution Model for High-Order Markov Chains and Non-Gaussian Time Series by André Berchtold and Adrian Raftery
- Paper with estimation algorithm implemented in the package An EM algorithm for estimation in the Mixture Transition Distribution model by Sophie Lèbre and Pierre-Yves Bourguinon.