In the context of a algorithms course, the Santa-Challenge could be solved as a voluntary exercise. This repository contains the code and a short description on how the exercise is solved. This challenge has originally been uploaded to kaggle.com in 2016.
Refer to the wiki for the description of the problem and for additional information.
See Result for the result achieved with the code in this repository.
Santa's magical sleigh has gone missing. Unfortunately, Christmas is very close and Santa does not want to cancel. Therefore, Santa needs the help of Computer-Science students with nothing better to do than to determine a tour to deliver the gifts as efficient as possible and to save Christmas.
Clone the git repository:
git clone https://github.com/Resistor10k1/santa-challenge.git
cd santa-challenge
And just run the build script:
bash build.sh
Or do it manually:
mkdir build && cd build
cmake ..
cmake --build . --target all
NOTE: If the Clang compiler is used, the libomp-dev library must be installed.
Jump into to build folder (cd build) and run the program. The program takes the relative path to the data file as an argument. If no argument is given, a small example data file is taken to show the program's functionality.
./santa-challenge "../data/gifts.csv"
Three different data files are available in the data folder:
- example_data.csv: A very small data set of 15 gifts. Suitable for a quick test-run of the program.
- small_gifts.csv: A small data set of 200 gifts. Suitable for testing.
- gifts.csv: The data set of 100'000 gifts, used to solve the challenge.
When the calculations are finished, the result is saved in the folder data. The format of the file is output_trips_<year>-<month>-<day>_<hour>-<minute>.csv.
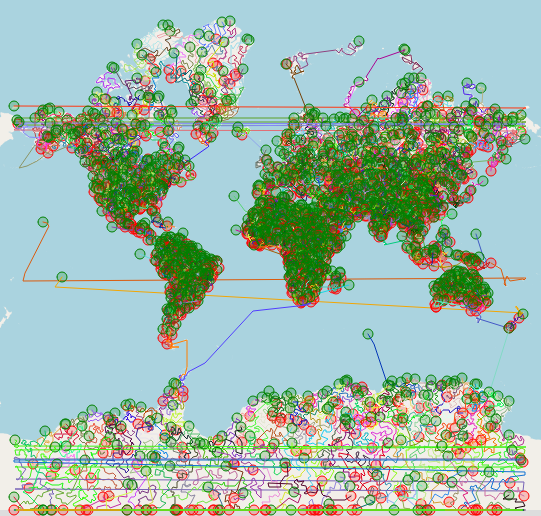
In a first step, all gifts are sorted by the distance to the North-Pole in ascending order. Starting with the closest gift, the tours are built with Nearest-Neighbour approach to find an initial solution. For each tour, a Simulated Annealing algorithm is run, to improve the existing tour and find a better solution.
Simulated-Annealing parameters:
| Parameter | Value |
|---|---|
| Neighbourhood size for 2-opt swapping | 25 |
| "Cooling" intervall with |
32 |
| "Reheating" intervall with |
128 |
| Initial temperature |
100'000 |
| Final temperature |
0.001 |
For verifing the solution a Jupyter notebook provided by the lecturer is used. The achieved weighted-reindeer-weariness is 13'449'226'461.1015 in 1430 trips. It took 20'749'713 ms => 5.76 h to find this solution.
The main work is done by the Nearest-Neighbour algorithm, because without Simulated-Annealing a
All tours are shown in Figure "Overview of all tours". All tours are also shown in an interactive map.
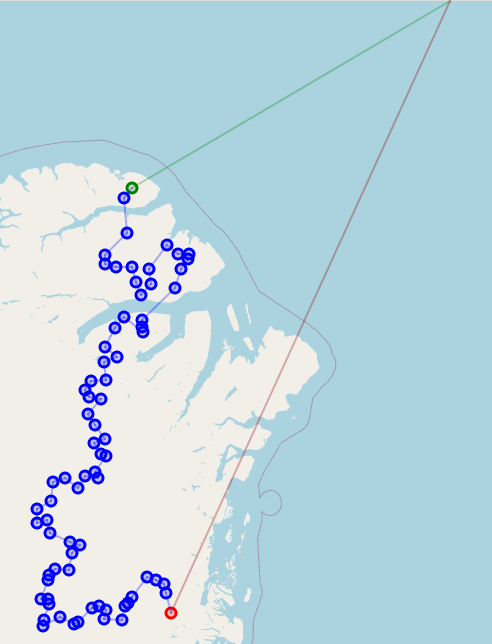
A single tour looks something like this:
All code is written in C++. For a detailed code documentation refer to this Link.
In general, just find 'a' solution and then try to improve it with local improvements such as k-opt Neighbourhood, Randomized Local Search or Simulated Annealing.
- Fill the sleigh with knapsack and the closest locations and optimize with some TSP algorithm.
- K-means clustering to group the locations which are close to each other. Apply some threshold (heuristics) for maximum distance within the group and also check that the sleigh weight is not exceeded. Start with the locations furthest away and optimize with some TSP algorithm.
How to cluster:
- Take the closest point p0 and add it to the sleigh.
- Check if the sleigh still has space and add the closest point to p0 to the sleigh. Repeat.
- Solve TSP locally in the found point subset. The two closest point to the pole are the start resp. end points.
- Restart