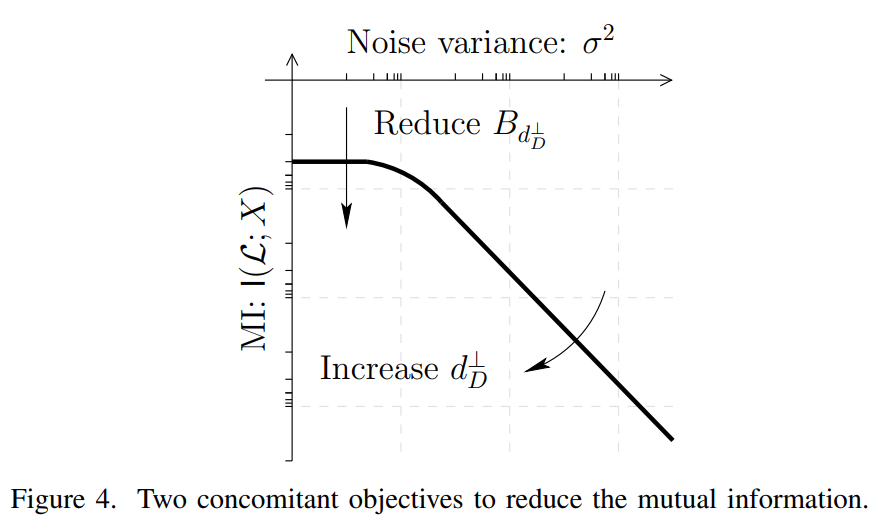
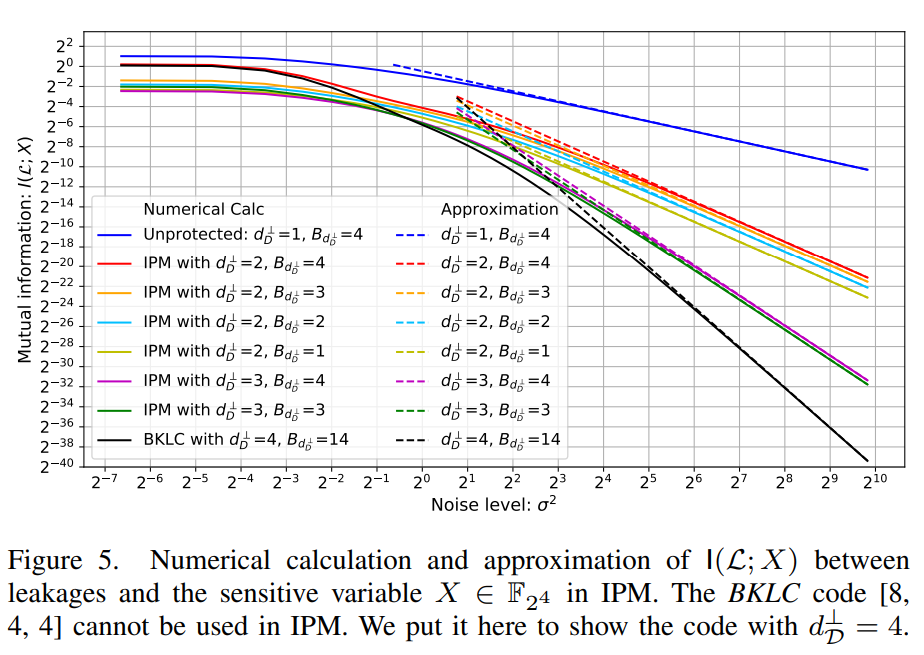
Open-source for Optimizing IPM by A Coding Theory Approach

This repo is created for the open-source of the paper Optimizing Inner Product Masking Scheme by A Coding Theory Approach, which was published by IEEE Transactions on Information Forensics and Security (T-IFS). All the data and scripts would allow researchers to verify and reproduce our results.

Basically, we present here the exhaustive study of all linear codes for Inner Product Masking (IPM)^[1,2] and show how to choose optimal linear codes for IPM. In particular, we give the optimal instances with n=2, 3 shares and l=4, 8 bits, respectively. All linear codes presented here are checked formally by Magma Computational Algebra System ^[3].

We recommend the Mathjax Plugin for Github on Chrome to have a better display of mathematical formulas.

1 Basics

1.1 Weight enumerator of a linear code

The weight enumerator ^[4] specifies the number of codewords of the same Hamming weights in a linear code $\mathcal{C}$. It is defined as:

It can also be denoted as: $[ (i, B_i), ~s.t. ~B_i\neq 0]$. We use the one further compact in this repository to save spaces. For instance, the weight enumerator of the code [8, 4, 4] is $[(0, 1), (4, 14), (8, 1)]$, then we write as $[0,1, 4, 14, 8, 1]$.

1.2 Equivalent codes

Two linear codes are said to be equivalent if one can be obtained from the other by a series of operations of the following two types:

an arbitrary permutation of the coordinate positions, and
in any coordinate position, multiplication by any nonzero scalar.

It is interesting to notice that equivalent linear codes have the same weight distribution.

2 Optimal codes for IPM

We present hereafter an exhaustive study of the linear codes for IPM, and show the optimal codes that can be a takeaway conclusion.

2.1 IPM with $n$=2 shares and $l$=4 bits

See here: Optimal codes IPM (n=2 & $l$=4).

The optimal codes are given in Tab. II in Section 2. We also present one example of BKLC code with parameter [8, 4, 4] which is better than all codes used in IPM. This BKLC code has been used in RSM (Rotating Sbox Masking) scheme during DPA Contest V4.1&4.2.

2.2 IPM with $n$=2 shares and $l$=8 bits

See here: Optimal codes IPM (n=2 & $l$=8).

The optimal codes are given in Tab. II in Section 2. We also present one example of BKLC code with parameter [16, 8, 5] which is better than all codes used in IPM.

2.3 IPM with $n$=3 shares and $l$=4 bits

See here: Optimal codes IPM (n=3 & $l$=4).

The optimal codes are given in Tab. II in Section 2. We also present one example of BKLC code with parameter [12, 4, 6], which is equivalent the best codes used in IPM.

2.4 IPM with $n$=3 shares and $l$=8 bits

See here: Optimal codes IPM (n=3 & $l$=8).

We present the weight enumerators of all 255*255=65025 linear codes for IPM. We omit the detaild tables for the sake of brevity, but only present all codes with maximized dual distance $d_{\mathcal{D}}^\perp$.

The optimal codes are given in Tab. II in Section 2. We also present one example of BKLC code with parameter [24, 8, 8], which is not as good as the best codes in IPM.

2.5 Information-theoretic evaluation ^[4]

We propose to use two parameters, the dual distance $d_{D}^\perp$ and the coefficient $B_{d_{D}^\perp}$, to characterize the side-channel resistance of IPM. The impact of two parameters on mutual informaiont are depicted as follows ^{[4, Fig. 4]}.

With $n$=2 shares and $l$=4 bits, all sixes classes of IPM codes and also one BKLC code are evaulated by using mutual information shown as follows ^{[4, Fig. 5]}.

3 Magma scripts

We share the Magma scripts to easily check the validity of our results. See here: Magma scripts. The corresponding logs are also provided here: Magma logs.

Copyright and License

This repository is placed into the public domain. Anyone can redistribute it and/or modify it under the GNU General Public License version 3.0.

Contacts

Wei Cheng (wei.cheng AT telecom-paris.fr)
Sylvain Guilley (sylvain.guilley AT secure-ic.com)

References

[1] Josep Balasch, Sebastian Faust, Benedikt Gierlichs, Clara Paglialonga, François-Xavier Standaert. Consolidating Inner Product Masking. ASIACRYPT (1) 2017: 724-754.

[2] Josep Balasch, Sebastian Faust, Benedikt Gierlichs. Inner Product Masking Revisited. EUROCRYPT (1) 2015: 486-510.

[3] Wieb Bosma, John Cannon, and Catherine Playoust, The Magma algebra system. I. The user language, J. Symbolic Comput., 24 (1997), 235–265. Accessed Jan 20, 2019.

[4] Wei Cheng, Sylvain Guilley, Claude Carlet, Sihem Mesnager and Jean-Luc Danger, Optimizing Inner Product Masking Scheme by A Coding Theory Approach. The IEEE Transactions on Information Forensics and Security, doi: 10.1109/TIFS.2020.3009609.

[5] Wei Cheng, Claude Carlet, Kouassi Goli, Jean-Luc Danger and Sylvain Guilley. Detecting Faults in Inner Product Masking Scheme - IPM-FD: IPM with Fault Detection. PROOFS 2019: 17-32, 2019.

Qomo-CHENG/OC-IPM