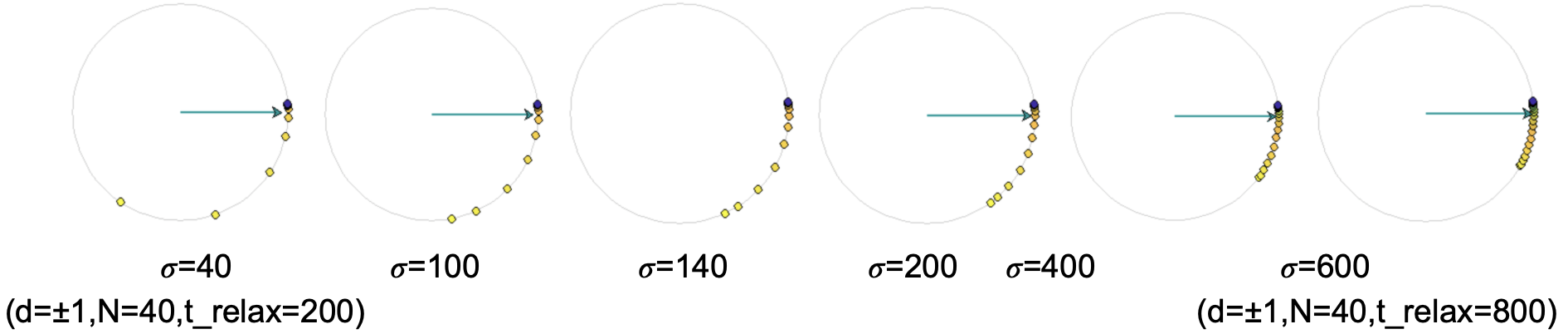/OSC-AD

Artifacts for "Physical Oscillator Model for Supercomputing"

Primary LanguageMATLAB

Artifact Description (AD) / Artifact Evaluation (AE)

Title: Physical Oscillator Model for Supercomputing

Table of Contents

A. Abstract

A parallel program together with the parallel hardware it is running on is not only a vehicle to solve numerical problems, it is also a complex system with interesting dynamical behavior: resynchronization and desynchronization of parallel processes, propagating phases of idleness, and the peculiar effects of noise and system topology are just a few examples. We propose a physical oscillator model (POM) to describe aspects of the dynamics of interacting parallel processes. Motivated by the well-known Kuramoto Model, a process with its regular compute-communicate cycles is modeled as an oscillator which is coupled to other oscillators (processes) via an interaction potential. Instead of a simple all-to-all connectivity as in the standard Kuramoto model, we employ a sparse topology matrix mapping the communication structure and thus the inter-process dependencies of the program onto the oscillator model and propose two interaction potentials that are suitable for different scenarios in parallel computing: resource-scalable and resource-bottlenecked applications. The former are not limited by a resource bottleneck such as memory bandwidth or network contention, while the latter are. As opposed to the original Kuramoto model, which has a periodic sinusoidal potential that is attractive for small angles, our characteristic potentials are always attractive for large angles and only differ in the short-distance behavior. We show that the model with appropriate potentials can mimic the propagation of delays and the synchronizing and desynchronizing behavior of scalable and bottlenecked parallel programs, respectively.

B. Description

We further provide an artifact description and an artifact evaluation appendix at https://doi.org/10.5281/zenodo.8386950. To allow a third party to duplicate the findings, this article describes the MATLAB source code for the implementation of the Physical Oscillator Model (POM) and the additional information about software environments and experimental design and method used for the results shown in the paper "Physical Oscillator Model for Supercomputing". It further contains videos and additional results that, owing to page restrictions, could not be included in this paper.

B.1 Check-list (artifact meta information)

  • B1.1.1 Algorithms and Programs: We used three MPI-parallel benchmarks.
1. MPI-parallel PISOLVER code -- mimics resource-scalable parallel programs -- calculates the value of pi using the midpoint rule with 500 M steps.
2. MPI-parallel STREAM Triad -- mimic resource-bottlenecked parallel programs -- sweep A(:)=B(:)+s*C(:) alternating with MPI pair-wise MPI_Irecv, MPI_Send and MPI_Wait routines.
3. MPI-parallel slow Schönauer vector Triad -- mimic resource-bottlenecked parallel programs --- sweep A(:)=B(:)+cos(C(:)/D(:)) alternating with MPI pair-wise MPI_Irecv, MPI_Send and MPI_Wait routines; the low-throughput cosine and floating-point division shifts the bandwidth saturation point to a higher number of cores.

The first code is scalable (no contention on memory interfaces, shared caches, or network interfaces), while the other two show saturation effects on ccNUMA domains due to memory bandwidth contention.

  • B1.1.2 Compilation: The C++ programming language is employed by all three MPI-parallel benchmarks. See below for details on compiler and MPI versions.
CXX: "mpiicpc"
STD optimizations: "-O3"
SIMD optimizations (Meggie): "-xHost -xAVX"
SIMD optimizations (SuperMUC-NG): "-xCORE-AVX512 -qopt-zmm-usage=high"
Intel Trace Analyzer and Collector, ITAC: "-trace"

  • B1.1.3 Binary
x86

  • B1.1.4 Hardware
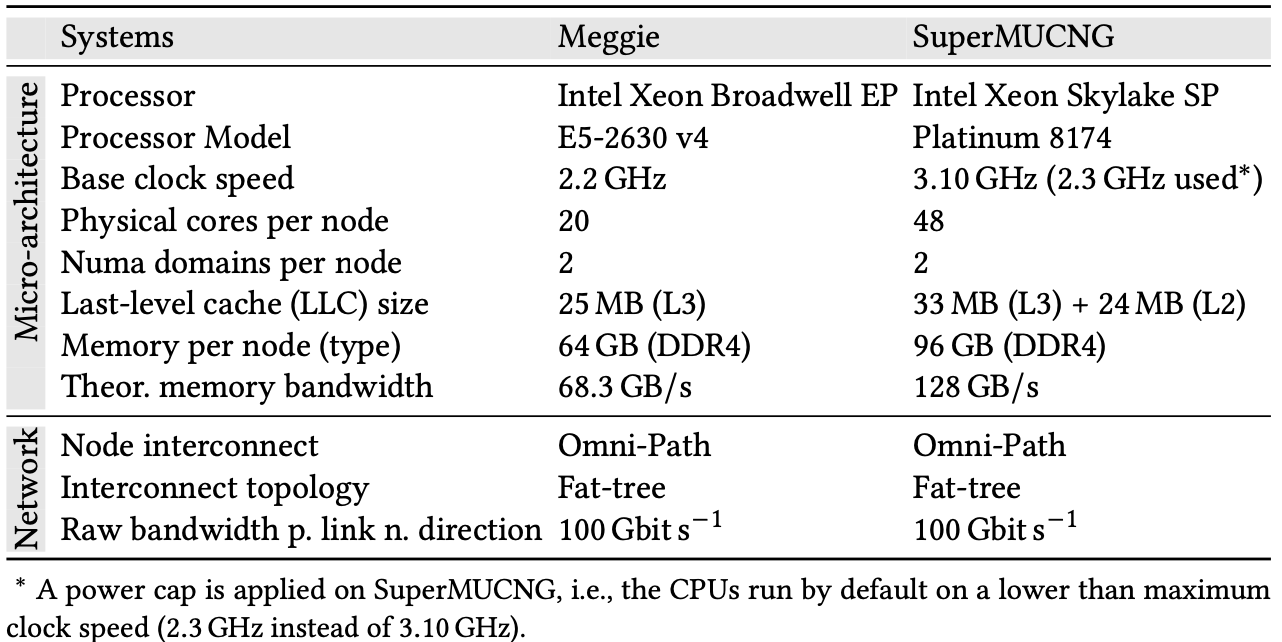
    To ensure the broad applicability of our results, we conducted most experiments on two systems having significant differences in the number of cores per ccNUMA domain and memory bandwidth per socket:
1. Meggie: 10 core Intel Xeon Broadwell E5-2630 v4 CPUs and fat-tree 100 Gbit/s Omni-Path 
2. SuperMUC-NG: 24 core Intel Xeon Skylake SP Platinum 8174 CPUs and fat-tree 100 Gbit/s Omni-Path

Key hardware specifications of systems are described below:

  • B1.1.5 Run-time environment and state: A comprehensive state description of the system that was utilized to conduct the experiments depicted in the paper's figures can be found in Meggie-state.csv. This lists comprehensive hardware information on

    • libraries and compilers along with their versions
    • operating system kernel, version and other details
    • CPUset
    • topology (cores, cache, NUMA)
    • NUMA balancing
    • general memory details
    • transparent huge pages
    • performance energy bias
    • hardware power limits

  • B1.1.6 Output

The work considers the runtime of each process at each iteration in seconds and the delay propagation speed in ranks/sec as primary metrics.

  • B1.1.7 Publicly available?
yes

B.2. How software can be obtained (if available)

To download the software, check out the following websites:

B.3. Hardware dependencies

Experiments were conducted on SuperMUC-NG (Intel Xeon Skylake SP CPUs) at a fixed clock frequency of 2.3 GHz (fixed, turbo disabled), and on Meggie (Intel Xeon Broadwell CPUs) at the base clock-frequency of 2.2 GHz (fixed, turbo disabled). The reproducibility of experiments requires mapping consecutive MPI processes to consecutive cores and fixing the frequency (i.e., switching off the turbo mode).

B.4. Software dependencies

The following versions of MATLAB and Intel Trace Analyzer and Collector (ITAC) were used.

  • MATLAB model's implementation, version 2023, update 0
  • MATLAB tool, version 2022, update R2022a
  • Intel Trace Analyzer and Collector, version 2021, update 6

Key software specifications on both systems are described below:

B.5. Datasets

  1. Resource-scalable parallel programs: The MPI-parallel PISOLVER code comprises a large number of back-to-back double-precision divide instructions, whose throughput is exactly one instruction per 16 clock cycles on Broadwell.

  2. Resource-bottlenecked parallel programs: Working sets were chosen large enough to not fit into any cache, which is at least 10x the last-level cache size, i.e., L3 caches (non-inclusive victim L3+L2 caches) in the Broadwell (Skylake) processors of Meggie (SuperMUC-NG). Data sharing across overlapping kernels was ruled out to eliminate the possibility of cache reuse.

    • MPI-parallel McCalpin STREAM TRIAD, A(:)=B(:)+s*C(:): An overall working set of 48 GB (2 x 10^9 elements) on Meggie and 1.2 GB (5 x 10^7 elements) on SuperMUC-NG is split evenly across the MPI processes, respectively.
    • MPI-parallel slow Schönauer TRIAD, A(:)=B(:)+cos(C(:)/D(:)): An overall working set of 1.6 GB (5 x 10^7 elements) on SuperMUC-NG is split evenly across the MPI processes.

    After each full loop traversal, each MPI rank i sends and receives data to and from each of its direct neighbors i + 1 and i - 1. The process topology is an open-chain.

C. Installation

Please install above-mentioned software dependencies.

D. Experiment workflow

To reproduce the experimental results, git clone the following repository:

git clone https://github.com/RRZE-HPC/OSC-AD && cd OSC-AD

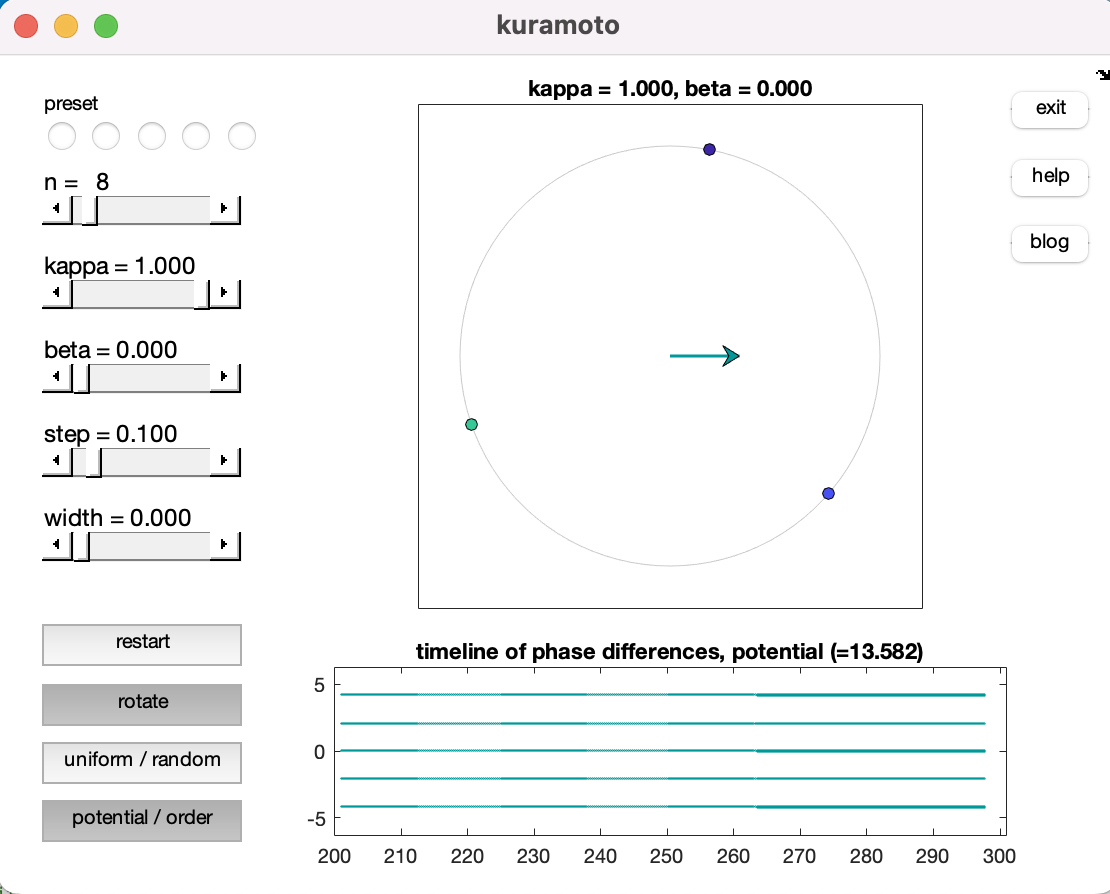
Run the kuramoto.m script and generate results using the available configuration options shown. Below is a sample output visualisation:

Defining communication topologies

Communication topologies topology(j,i) of MPI-parallel micro-benchmarks are described below.

topology = zeros(n);
for i = 1:N
    for j = 1:N  
    	x = j-i;
        d = ...; % 1 (next) or 2 (next-to-next) communication only
        if ...
        (x == d) % lower dth sub-diagonal (non-periodic)
        (-x == d) % upper dth sub-diagonal (non-periodic)
        ((-x == d) | (x == n-d)) % upper dth and lower (n-d)th sub-diagonal (periodic)
        ((x == d) | (-x == n-d)) % lower dth and upper (n-d)th sub-diagonal (periodic)
        (abs(x) == d) % both upper and lower dth sub-diagonal (non-periodic)
        ((abs(x) == d) | (abs(x) == n-d)) % both upper and lower dth and (n-d)th sub-diagonals (periodic) 
            topology(j,i) = 1;
        end       
    end
end

E. Evaluation and expected result

Run the MATLAB implementation according to the README file and compare the results in the paper. Validation of our Physical Oscillator Model (POM) was done by applying comparison with experimental collected traces on two platforms. Navigate to the links of Google documents, mentioned in Section G of this article, or to the videos repository to access the videos of stored measured results. If executed on the same hardware as described, we anticipate that these figures will be close to those in the paper.

F. Experiment customization

We took a number of measures to create a reproducible experimental environment and minimize any noise from system sources. Before actual measurements were taken, at least 50 warm-up time steps with barrier synchronization were performed to allow the MPI runtimes to settle and eliminate first-call overhead. In MPI programs, noise or one-off delays were generated by extending the computational phase on certain MPI ranks via doing extra work.

G. Results analysis discussion

Communication delays for non-blocking calls were measured by time spent in the MPI_Waitall function.

Boilerplate graphical visualization output

In the figure above POMviz.png, we show the output from the MATLAB model's implementation. Beyond the circle diagram option for result visualization, implementation display two further options:

  1. the timeline of phase differences for oscillators
  2. the timeline of potentials

See Listings below for both.

  1. Timeline visualization of phase-differences for oscillators.

    for j = 1:length(t)
    g=dot(topology,theta(:,j)-theta(:,j)',2)
    fprintf(outputfile,'%6.3f %6.3f \n',t,g); 
end

  2. Boilerplate graphical visualization for potential.

    for j = 1:length(t)
    v=sum(dot(topology,tanh(abs(theta(:,j)-theta(:,j)')),2))
    fprintf(outputfile,'%6.3f %6.3f \n',t,v);
end

Impact of sigma for resource-bottlenecked programs

The following figure shows the effect of sigma (from Equation 4 of paper) on the resource-bottlenecked programs.

sigma.png

Videos: MPI programs analogy with POM

Two communication topologies are considered for each case:

  1. d=+-1, i.e., process P_i send and receive from P_{i+1} and P_{i-1} processes
  2. d=+-1, -2, i.e., process P_i receive from P_{i+1} and P_{i-1}, while send to P_{i+1}, P_{i-1} and P_{i-2}

POM results for analogy with two MPI-parallel codes were considered for two systems; press the play button to watch the videos showing 30 iterations.

H. Summary

Please see the Section 6 of the paper for a summary.

I. Notes

Please cite the work as:

Bibtex:

@INPROCEEDINGS{POM2023,
author={Afzal, Ayesha and Hager, Georg and Wellein, Gerhard},
booktitle={2023 IEEE/ACM Performance Modeling, Benchmarking and Simulation of High Performance Computer Systems (PMBS)},
title={Physical Oscillator Model for Supercomputing},
year={2023},
doi={10.1145/3624062.3625535}}

  • A. Afzal, G. Hager, and G. Wellein: Physical Oscillator Model for Supercomputing -- Data Artifact Appendix. DOI:10.5281/zenodo.8386950

Bibtex:

@INPROCEEDINGS{POMAD2023,
author={Afzal, Ayesha and Hager, Georg and Wellein, Gerhard},
booktitle={[online]},
title={Physical Oscillator Model for Supercomputing {--} Data Artifact Appendix},
year={2023},
doi={10.5281/zenodo.8386950}}