A time-resolved theory of information encoding in recurrent neural networks

This repository contains the implementation code for manuscript:
A time-resolved theory of information encoding in recurrent neural networks

Overview

In this work, we show theoretically and empirically that more tightly balanced networks can track time-varying signals more reliably which results in a higher information rate. Moreover, this example code demonstrates how training an RNN on tracking a time-varying input makes it more tightly balanced, and tracking on multiple stimuli leads to the emergence of tightly balanced subnetworks that are weakly connected in between.

Installation

Prerequisites

Download Julia

Dependencies

Julia (>= 1.5, tested on 1.6)
Flux, PyPlot, Statistics, DelimitedFiles,RandomNumbers, ForwardDiff, BSON
scipy

Getting started

To install the required packages, run the following in the julia REPL after installing Julia:

using Pkg

for pkg in ["Flux", "PyPlot", "Statistics", "DelimitedFiles", "RandomNumbers", "ForwardDiff", "BSON"]
    Pkg.add(pkg)
end

For example, to train an RNN on tracking two OU-signals, run:

include("example_code/runOneStimulus.jl")
end

Repository Overview

src/

Contains the source files.
generateInputOutputOUAnalytical.jl - solves the OU-process distributionally correct to generate input and target output.
trainingBalancedNets.jl - trains a RNN on the autoencoder task and visualizes the results during training.

example_code/

Example scripts for training networks on one, two and three stimuli.
runOneStimulus.jl trains an RNN on tracking one OU-signal showing that the network becomes more tightly balanced over training epochs.
runTwoStimuli.jl trains an RNN on two OU-signal stimulus showing that the network becomes more tightly balanced over training epochs and breaks up into two weakly-connected subnetworks.
runTheeStimuli.jl trains an RNN on two OU-signal stimulus showing that the network becomes more tightly balanced over training epochs and breaks up into three weakly-connected subnetworks.

Training dynamics of eigenvalues:

Here is a visualization of the recurrent weight matrix and the eigenvalues throughout across training epochs.

Implementation details

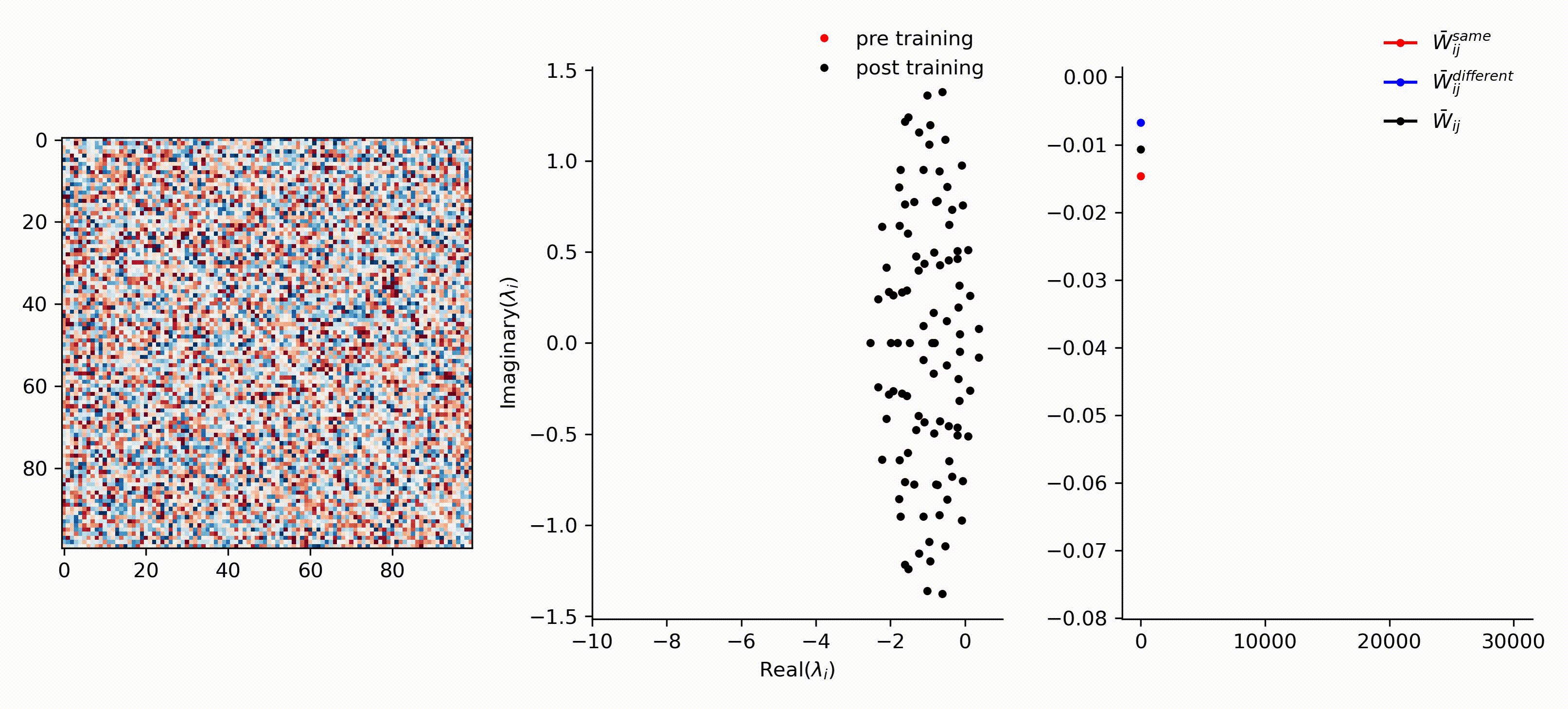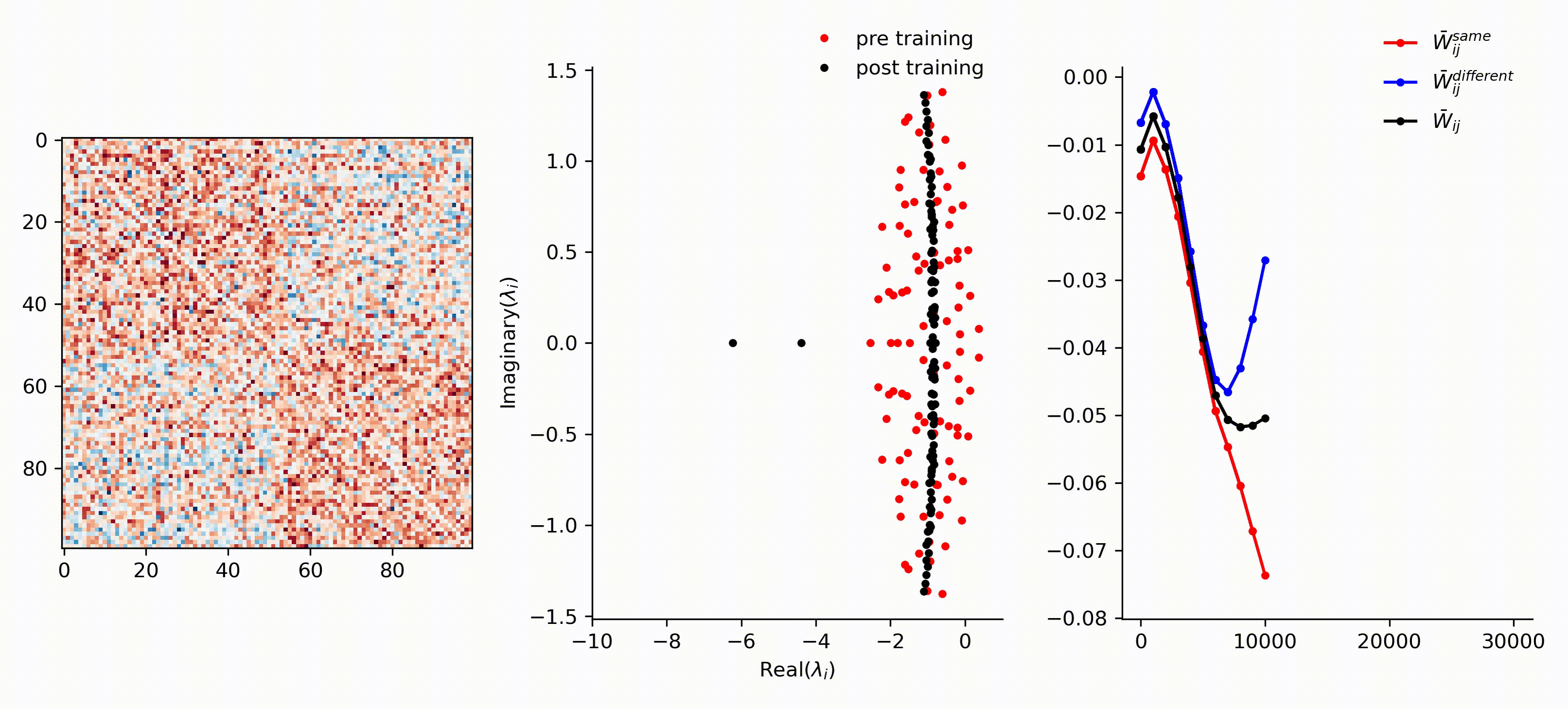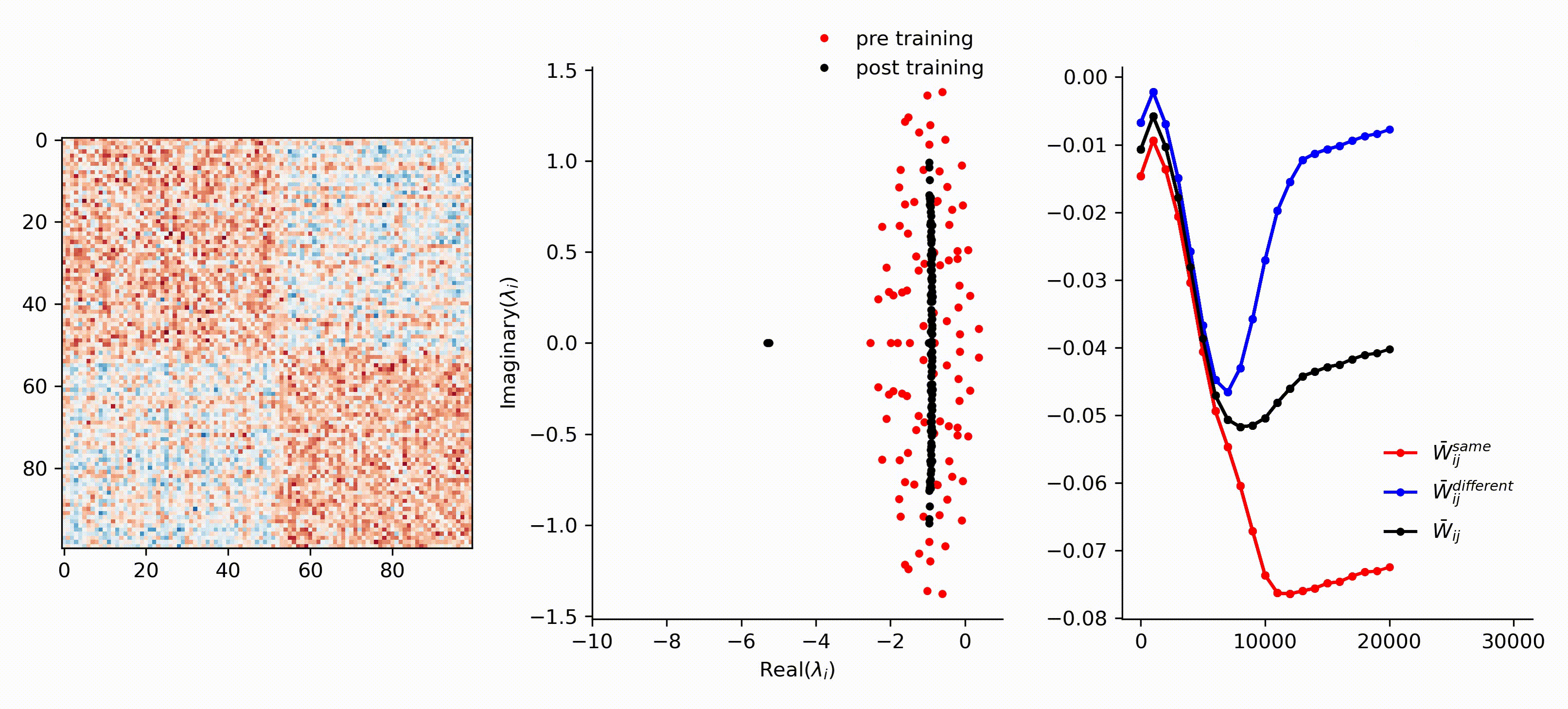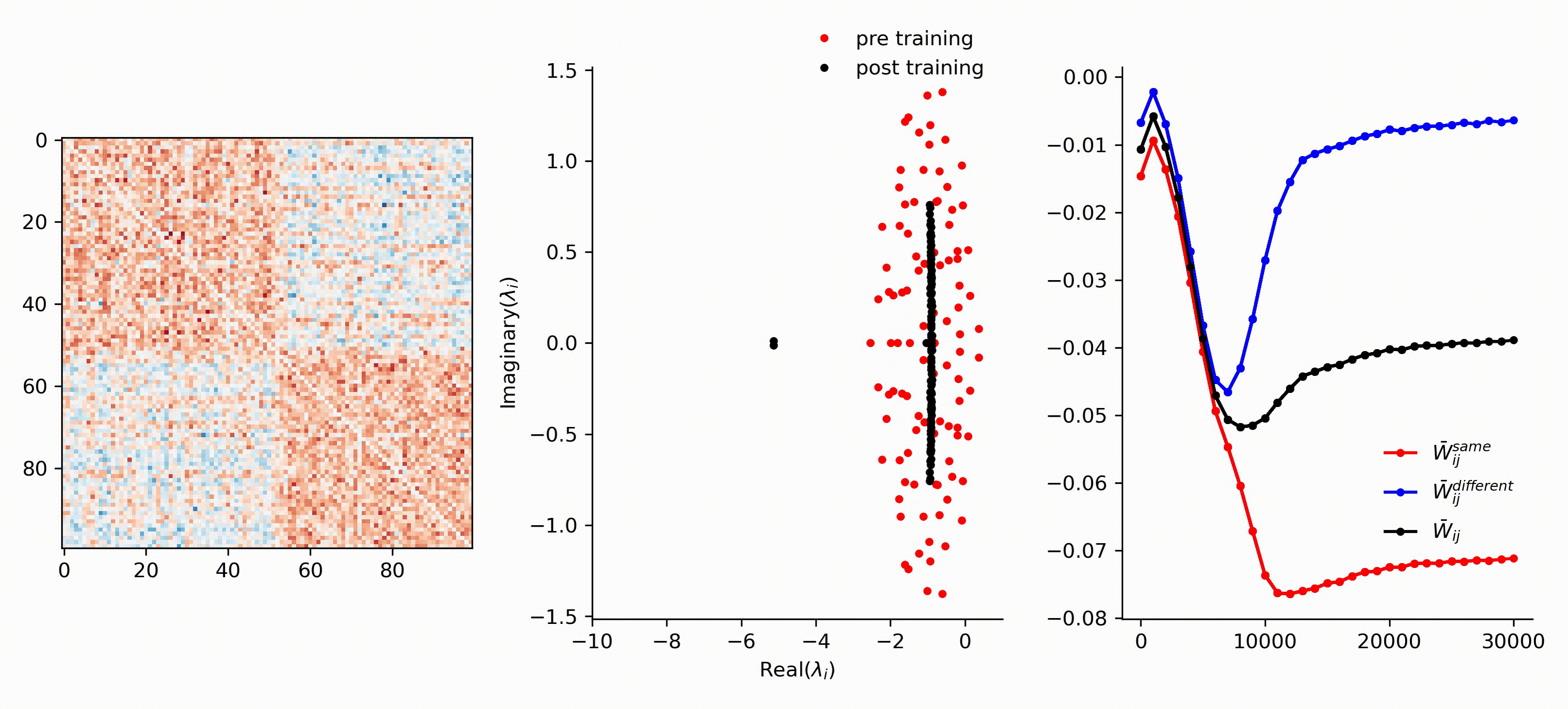
A full specification of packages used and their versions can be found in packages.txt .
Results were found not to depend strongly on details of parameters (e.g. temporal discretization dt, network size N, batch size B etc).
For learning rates the default ADAM parameters were used to avoid any impression of fine-tuning.
For all calculations, a 'burn-in' period was discarded to let the network state converge to a stationary state.
All simulations were run on a single CPU and took on the order of minutes to a few of hours.

RainerEngelken/NeurIPS2022