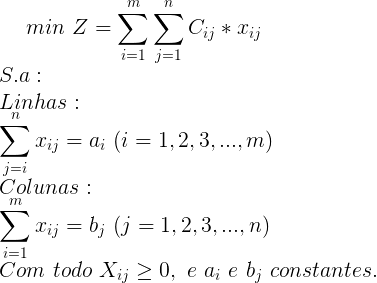Aplicação em python com uso do método simplex para otimizar entregas de uma rede de farmácias.
Desenvolver um programa com o fim de aplicar uma modelagem para minimização do custo de entregas entre farmácias e clientes. Foi considerado como custo a distância entre as lojas e os destinos, para assim determinar quais estabelecimentos devem fazer a entrega a um certo cliente de modo a minimizar o custo, levando em consideração o estoque de cada loja e a quantidade requisitada em cada pedido.
Esta é a modelagem que minimiza o custo de transporte, e que será usada no método simplex:
Este algoritmo, necessita de dois aquivos .csv, que são "farmacias.csv" e "solicitacoes.csv", ambos contém um índice, latitude, longitude e estoque ou demanda, separados por vírgula. Como no exemplo:
- "farmacias.csv"
| Loja | Latitude | Longitude | Estoque |
|---|---|---|---|
| 1 | -16.751524 | -43.879035 | 50 |
| 2 | -16.713941 | -43.853944 | 50 |
| 3 | -16.740076 | -43.870815 | 50 |
- "solicitacoes.csv"
| Cliente | Latitude | Longitude | Solicitação |
|---|---|---|---|
| 1 | -16.690414 | -43.836981 | 5 |
| 2 | -16.713023 | -43.837304 | 45 |
| 3 | -16.730625 | -43.857152 | 100 |
Após os arquivos serem lidos, as coordenadas são armazenadas e é calculada a distância de todas as lojas para cada solicitação utilizando a Fórmula de Haversine, que é uma importante equação usada em navegação, fornecendo distâncias entre dois pontos no globo a partir de suas latitudes e longitudes, estas serão o custo de transporte de cada loja para cada cliente.
- Tabela do Problema Inicial
| Lojas | S1 | S2 | S3 | Estoque |
|---|---|---|---|---|
| L1 | 8 | 6 | 3 | 50 |
| L2 | 3 | 2 | 2 | 50 |
| L3 | 7 | 5 | 2 | 50 |
| Solicitação | 5 | 45 | 100 | --- |
Com esses dados obtemos a função objetivo e restrições:
Z = 8x1 + 6x2+ 3x3 + 3x4 + 3x5 + 3x6 + 7x7 + 5x8 + 2x9
Sujeito a:
x1 + x2 + x3 <= 50
x4 + x5 + x6 <= 50
x7 + x8 + x9 <= 50
x1 + x4 + x7 = 5
x2 + x6 + x8 = 45
x3 + x7 + x9 = 100
x1, x2, x3, x4, x5, x6, x7, x8, x9 >= 0
Estas restrições são organizadas para servirem como entrada para o sistema de solução online para otimização de transporte, desenvolvido na CEFET-MG, sisponível no seguinte endereço: SIMO.
Por final, o algoritmo gera um arquivo txt da modelagem que pode ser transferido para o SIMO que gera a solução de forma clara, por meio de tabelas, indicando as lojas de saída, quantidade e clientes de destino.
- Solução para o exemplo acima
| Loja | Quant. | Cliente |
|---|---|---|
| 1 | 50 | 3 |
| 2 | 5 | 1 |
| 2 | 45 | 2 |
| 3 | 50 | 3 |
| Custo Total: | 10.0 Km | |
| Número de Farmácias: | 3 | |
| Número de Clientes: | 3 |
Caso o problema seja desbalanceado, o algoritmo fará o tratamento automático adicionando as variáveis fantasmas para balanceá-lo e alertará o usuário.
Para executar esse algoritmo, é necessesário ter instalado o python (v. 3.7.5) ou superior, o numpy (v. 1.17.4).
Para rodar pelo terminal, utilize o seguinte comando no diretório do algoritmo:
python3 otimiza.py <csv_fornecimento> <csv_destinos>
Especificando os dois arquivos csv correspondentes as lojas e aos clientes, conforme exemplificado anteriormente.
-
Mirrális Dias Santana - Graduando em Ciência da Computação - IFNMG - Montes Claros/MG
-
Reinaldo Junio Dias de Abreu - Graduando em Ciência da Computação - IFNMG - Montes Claros/MG
Aplicação desenvolvida como trabalho de conclusão para disciplina de Pesquisa Operacional, ministrada pela professora Luciana Balieiro Cosme.