PINO

Physics-informed Neural Operator for Learning Partial Differential Equation

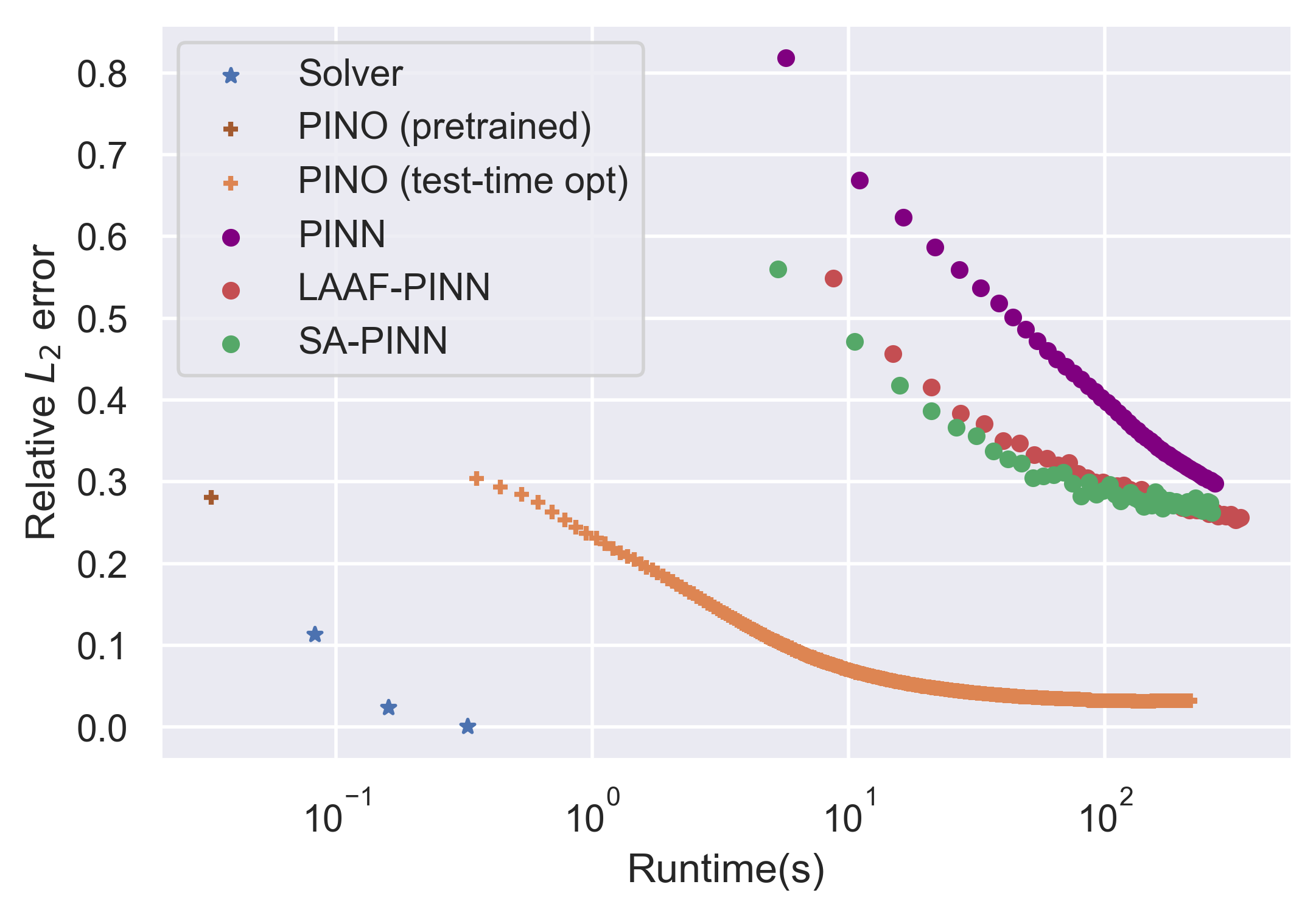
Abstract: Machine learning methods have recently shown promise in solving partial differential equations (PDEs). They can be classified into two broad categories: solution function approximation and operator learning. The Physics-Informed Neural Network (PINN) is an example of the former while the Fourier neural operator (FNO) is an example of the latter. Both these approaches have shortcomings. The optimization in PINN is challenging and prone to failure, especially on multi-scale dynamic systems. FNO does not suffer from this optimization issue since it carries out supervised learning on a given dataset, but obtaining such data may be too expensive or infeasible. In this work, we propose the physics-informed neural operator (PINO), where we combine the operating-learning and function-optimization frameworks, and this improves convergence rates and accuracy over both PINN and FNO models. In the operator-learning phase, PINO learns the solution operator over multiple instances of the parametric PDE family. In the test-time optimization phase, PINO optimizes the pre-trained operator ansatz for the querying instance of the PDE. Experiments show PINO outperforms previous ML methods on many popular PDE families while retaining the extraordinary speed-up of FNO compared to solvers. In particular, PINO accurately solves long temporal transient flows and Kolmogorov flows, while PINN and other methods fail to converge.

Requirements

Pytorch 1.8.0 or later
wandb
tqdm
scipy
h5py
numpy
DeepXDE:latest
Latest code from tensordiffeq github master branch (Not tensordiffeq 0.19)
tensorflow 2.4.0

Data description

Burgers equation

burgers_pino.mat

Darcy flow

spatial domain: $x\in (0,1)^2$
Data file: piececonst_r421_N1024_smooth1.mat, piececonst_r421_N1024_smooth2.mat
Raw data shape: 1024x421x421

Long roll out of Navier Stokes equation

spatial domain: $x\in (0, 1)^2$
temporal domain: $t\in [0, 49]$
forcing: $0.1(\sin(2\pi(x_1+x_2)) + \cos(2\pi(x_1+x_2)))$
viscosity = 0.001

Data file: nv_V1e-3_N5000_T50.mat, with shape 50 x 64 x 64 x 5000

train set: -1-4799
test set: 4799-4999

Navier Stokes with Reynolds number 500

spatial domain: $x\in (0, 2\pi)^2$
temporal domain: $t \in [0, 0.5]$
forcing: $-4\cos(4x_2)$
Reynolds number: 500

Train set: data of shape (N, T, X, Y) where N is the number of instances, T is temporal resolution, X, Y are spatial resolutions.

NS_fft_Re500_T4000.npy : 4000x64x64x65
NS_fine_Re500_T128_part0.npy: 100x129x128x128
NS_fine_Re500_T128_part1.npy: 100x129x128x128

Test set: data of shape (N, T, X, Y) where N is the number of instances, T is temporal resolution, X, Y are spatial resolutions.

NS_Re500_s256_T100_test.npy: 100x129x256x256
NS_fine_Re500_T128_part2.npy: 100x129x128x128

Configuration file format: see .yaml files under folder configs for detail.

Code for Burgers equation

Train PINO

To run PINO for Burgers equation, use, e.g.,

python3 train_burgers.py --config_path configs/pretrain/burgers-pretrain.yaml --mode train

To test PINO for burgers equation, use, e.g.,

python3 train_burgers.py --config_path configs/test/burgers.yaml --mode test

Code for Darcy Flow

Operator learning

To run PINO for Darcy Flow, use, e.g.,

python3 train_operator.py --config_path configs/pretrain/Darcy-pretrain.yaml

To evaluate operator for Darcy Flow, use, e.g.,

python3 eval_operator.py --config_path configs/test/darcy.yaml

Test-time optimization

To do test-time optimization for Darcy Flow, use, e.g.,

python3 run_pino2d.py --config_path configs/finetune/Darcy-finetune.yaml --start [starting index] --stop [stopping index]

Baseline

To run DeepONet, use, e.g.,

python3 deeponet.py --config_path configs/pretrain/Darcy-pretrain-deeponet.yaml --mode train

To test DeepONet, use, e.g.,

python3 deeponet.py --config_path configs/test/darcy.yaml --mode test

Code for Navier Stokes equation

Train PINO for short time period

To run operator learning, use, e.g.,

python3 train_operator.py --config_path configs/pretrain/Re500-pretrain-05s-4C0.yaml

To evaluate trained operator, use

python3 eval_operator.py --config_path configs/test/Re500-05s.yaml

To run test-time optimization, use

python3 train_PINO3d.py --config_path configs/***.yaml

To train Navier Stokes equations sequentially without running train_PINO3d.py multiple times, use

python3 run_pino3d.py --config_path configs/[configuration file name].yaml --start [index of the first data] --stop [which data to stop]

Baseline for short time period

To train DeepONet, use

python3 deeponet.py --config_path configs/[configuration file].yaml --mode train

To test DeepONet, use

python3 deeponet.py --config_path configs/[configuration file].yaml --mode test

To train and test PINNs, use, e.g.,

python3 pinns.py --config_path configs/baseline/Re500-pinns-05s.yaml --start [starting index] --stop [stopping index]

To train and test LAAF-PINN, use, e.g.,

python3 pinns.py configs/baseline/Re500-pinns-05s-LAAF.yaml --start [starting index] --stop [stopping index]

To train and test SA-PINNs, first copy the latest code of tensordiffeq under the working directory. Then run:

DDEBACKEND=pytorch python3 pinns.py configs/baseline/Re500-pinns-05s-SA.yaml --start [starting index] --stop [stopping index]

Baseline for long roll out

To train and test PINNs, use

python3 pinns.py --config_path configs/baseline/NS-50s.yaml --start [starting index] --stop [stopping index]