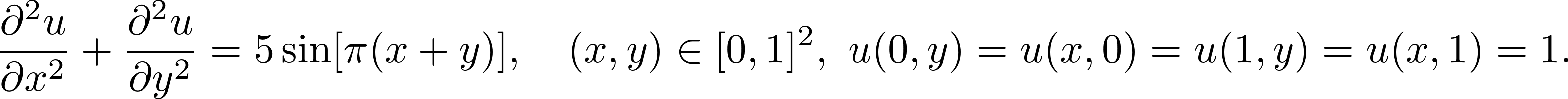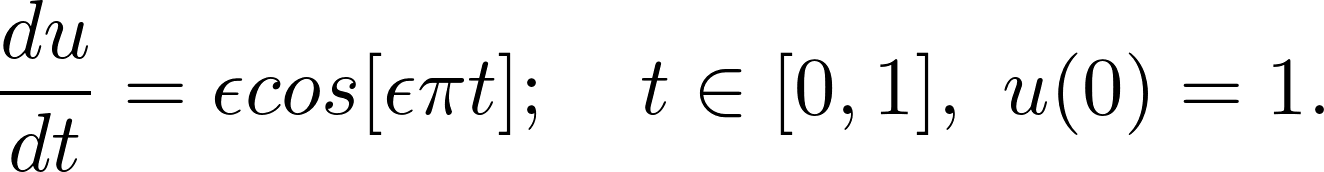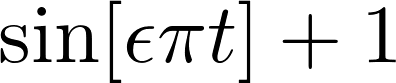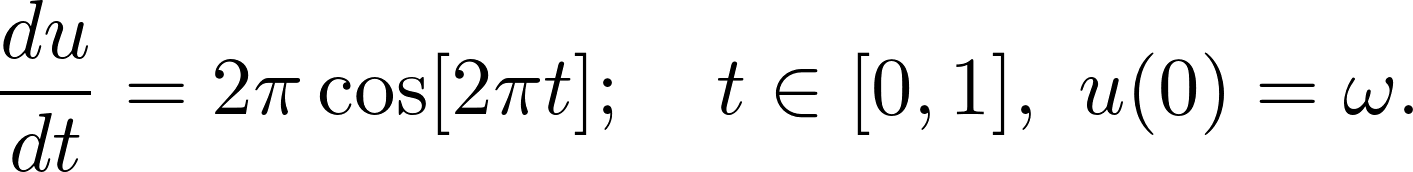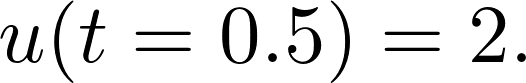PyDEns

PyDEns is a framework for solving Ordinary and Partial Differential Equations (ODEs & PDEs) using neural networks. With PyDEns one can solve

PDEs & ODEs from a large family including heat-equation, poisson equation and wave-equation
parametric families of PDEs
PDEs with trainable coefficients.

This page outlines main capabilities of PyDEns. To get an in-depth understanding we suggest you to also read the tutorial.

Getting started with PyDEns: solving common PDEs

Let's solve poisson equation

using simple feed-forward neural network with tahn-activations. The first step is to add a grammar of tokens - expressions used for writing down differential equations - to the current namespace:

from pydens import Solver, NumpySampler, add_tokens
import numpy as np

add_tokens()
# we've now got functions like sin, cos, D in our namespace. More on that later!

You can now set up a PyDEns-model for solving the task at hand using configuration dictionary. Note the use of differentiation token D and sin-token:

pde = {'n_dims': 2,
       'form': lambda u, x, y: D(D(u, x), x) + D(D(u, y), y) - 5 * sin(np.pi * (x + y)),
       'boundary_condition': 1}

body = {'layout': 'fa fa fa f',
        'units': [15, 25, 15, 1],
        'activation': [tf.nn.tanh, tf.nn.tanh, tf.nn.tanh]}

config = {'body': body,
          'pde': pde}

us = NumpySampler('uniform', dim=2) # procedure for sampling points from domain

and run the optimization procedure

dg = Solver(config)
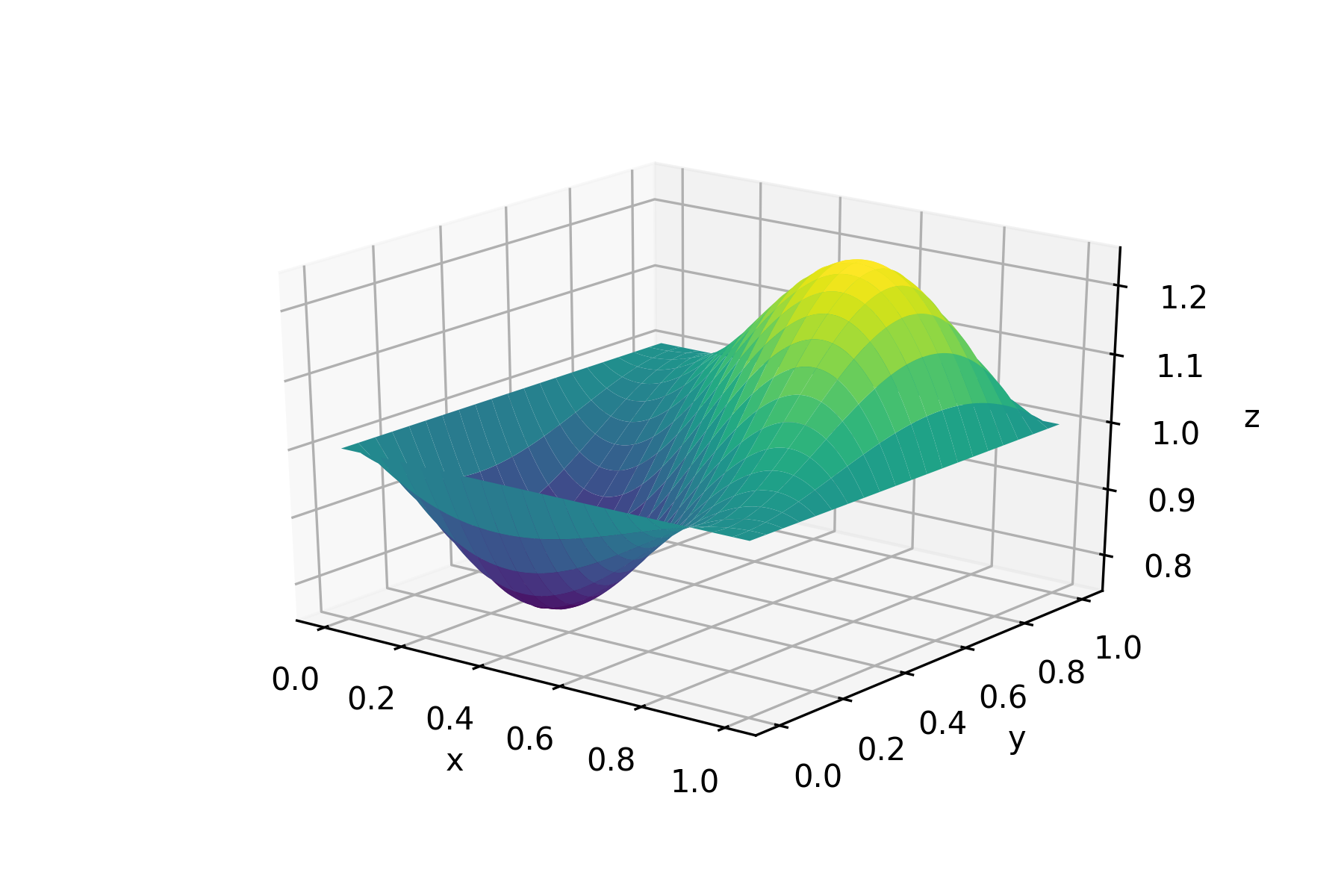
dg.fit(batch_size=100, sampler=us, n_iters=1500)

in a fraction of second we've got a mesh-free approximation of the solution on [0, 1]X[0, 1]-square:

Going deeper into PyDEns-capabilities

PyDEns allows to do much more than just solve common PDEs: it also deals with (i) parametric families of PDEs and (ii) PDEs with trainable coefficients.

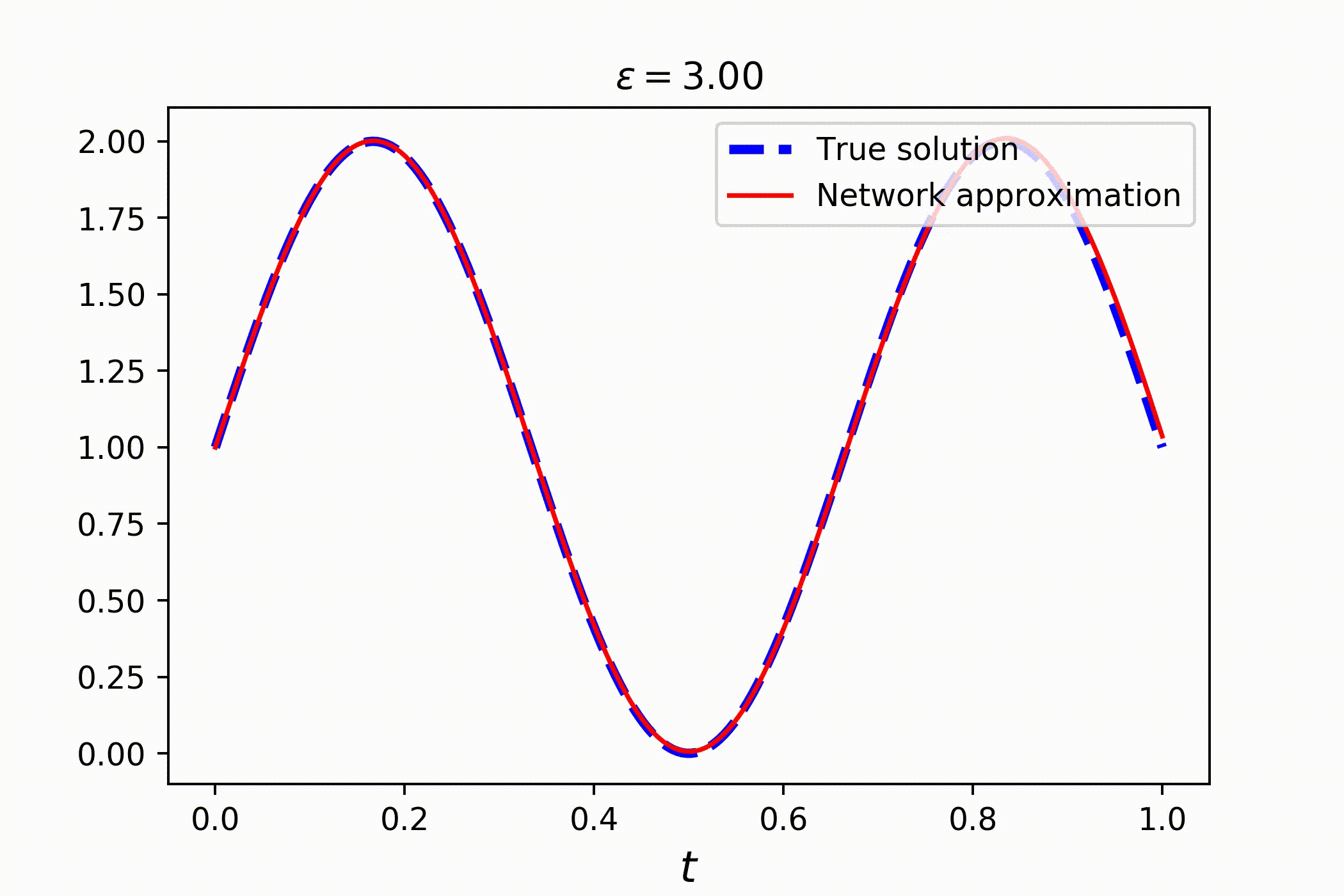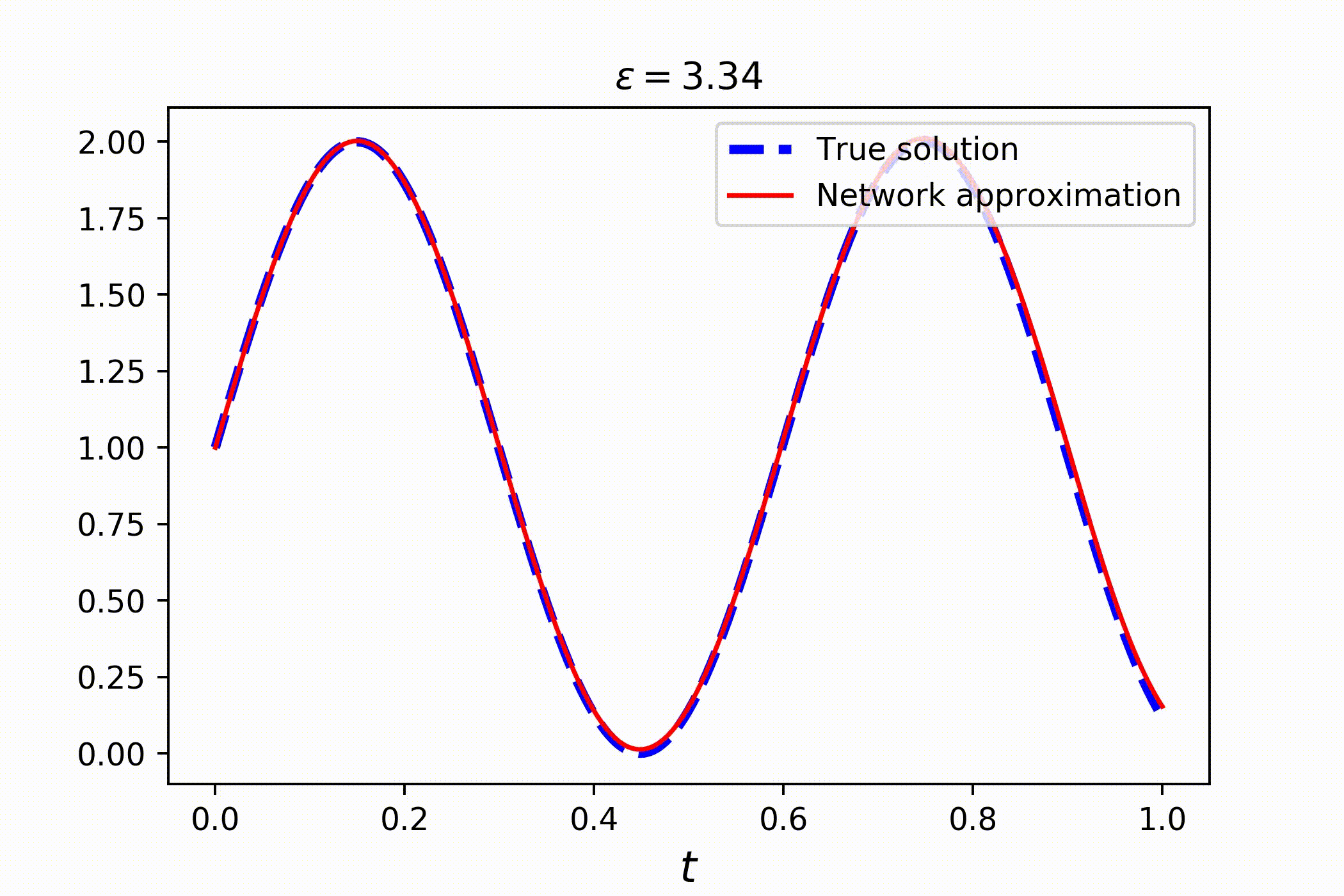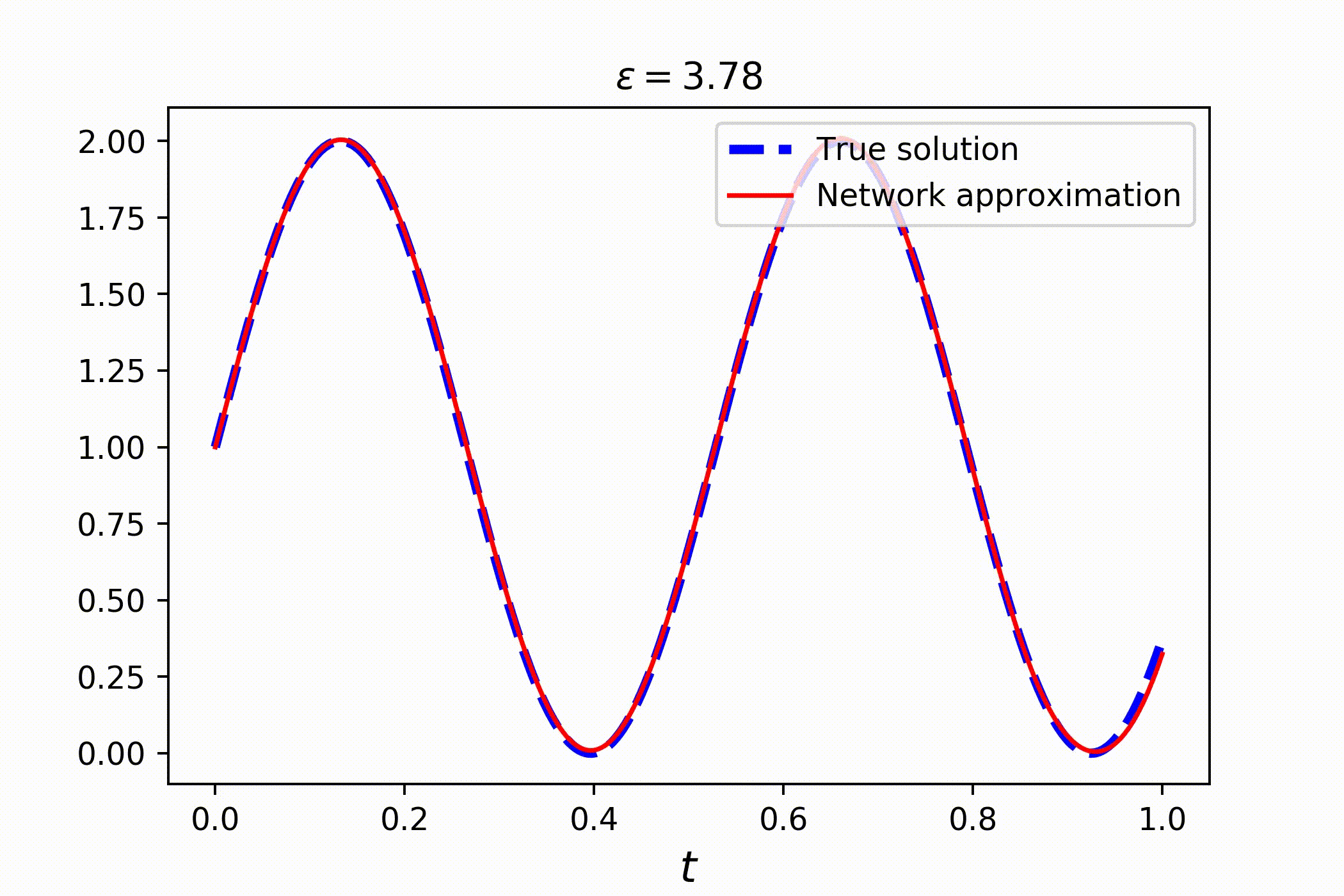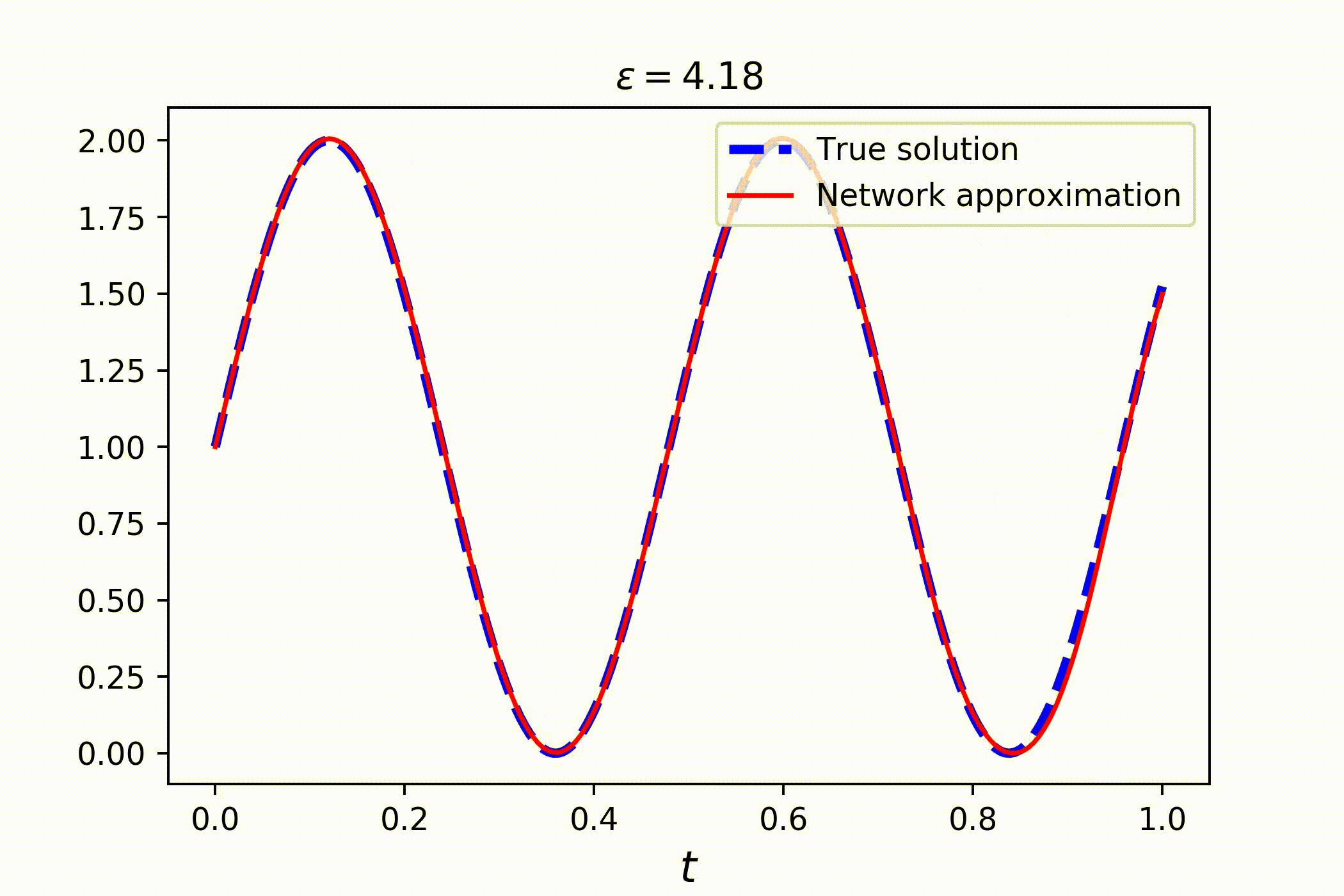
Solving parametric families of PDEs

Consider a family of ordinary differential equations

Clearly, the solution is a sin wave with a phase parametrized by ϵ:

Solving this problem is just as easy as solving common PDEs. You only need to introduce parameter in the equation, using token P:

pde = {'n_dims': 1,
       'form': lambda u, t, e: D(u, t) - P(e) * np.pi * cos(P(e) * np.pi * t),
       'initial_condition': 1}

config = {'pde': pde}
# One for argument, one for parameter
s = NumpySampler('uniform') & NumpySampler('uniform', low=1, high=5)

dg = Solver(config)
dg.fit(batch_size=1000, sampler=s, n_iters=5000)
# solving the whole family takes no more than a couple of seconds!

Check out the result:

Solving PDEs with trainable coefficients

With PyDEns things can get even more interesting! Assume that the initial state of the system is unknown and yet to be determined:

Of course, without additional information, the problem is undefined. To make things better, let's fix the state of the system at some other point:

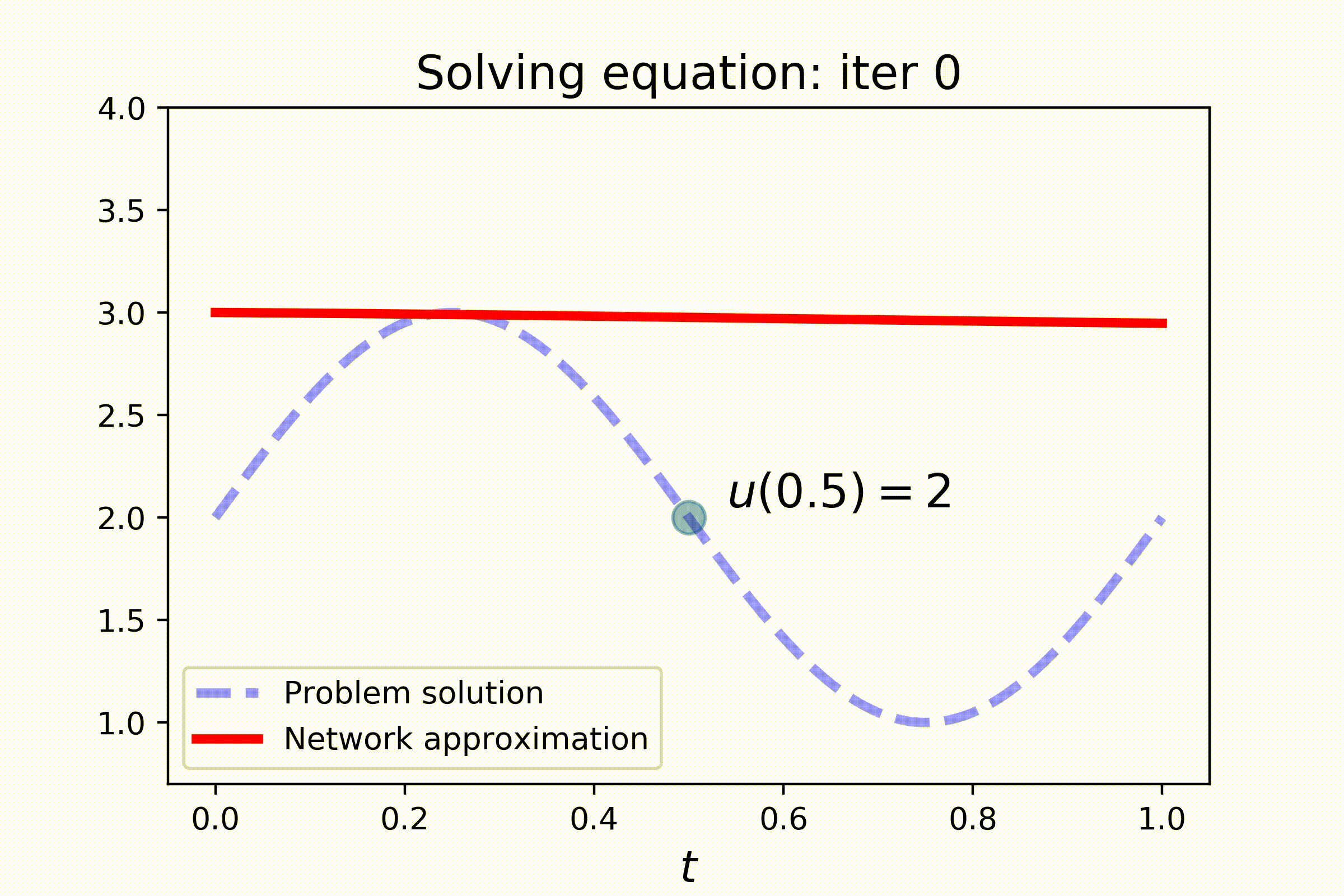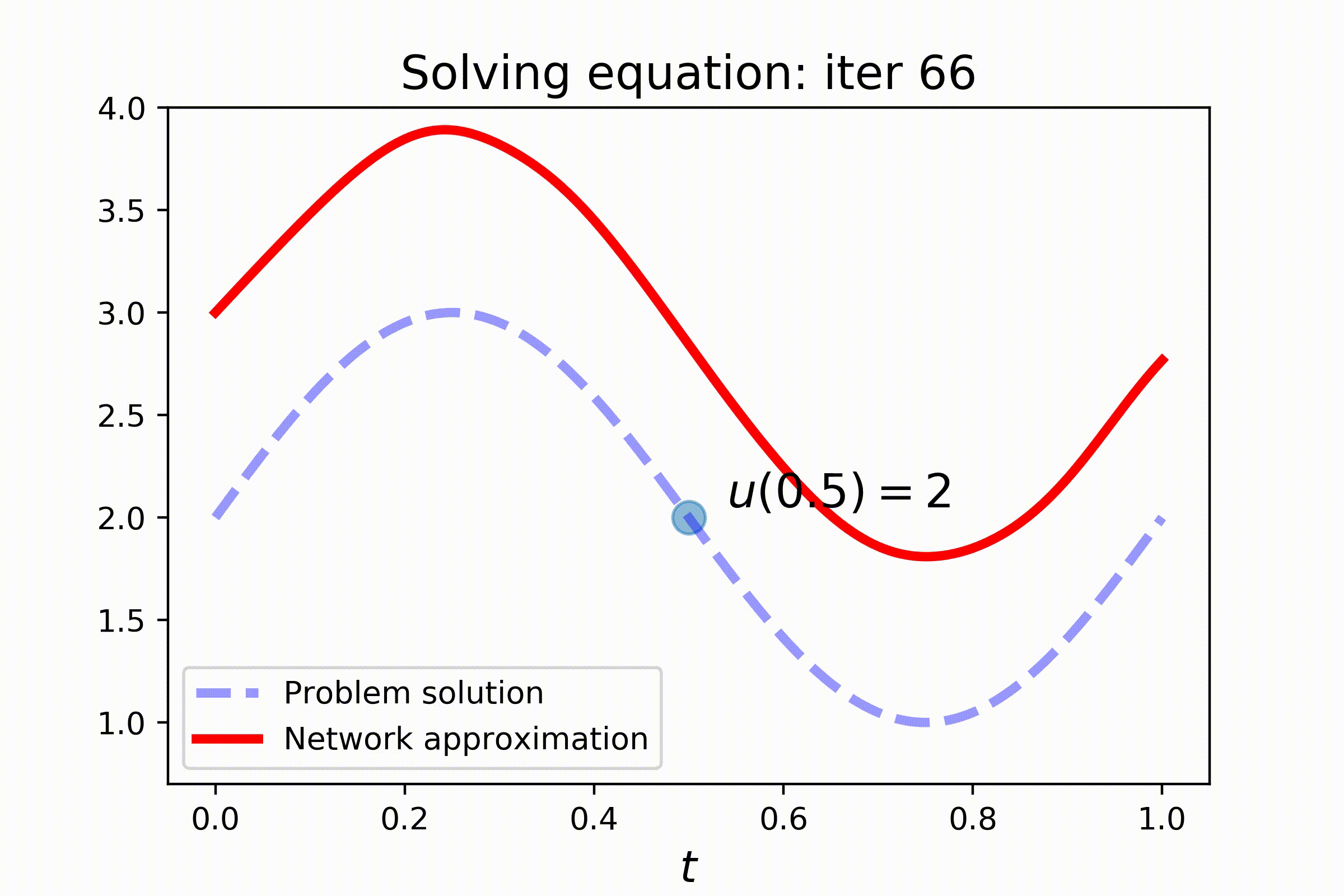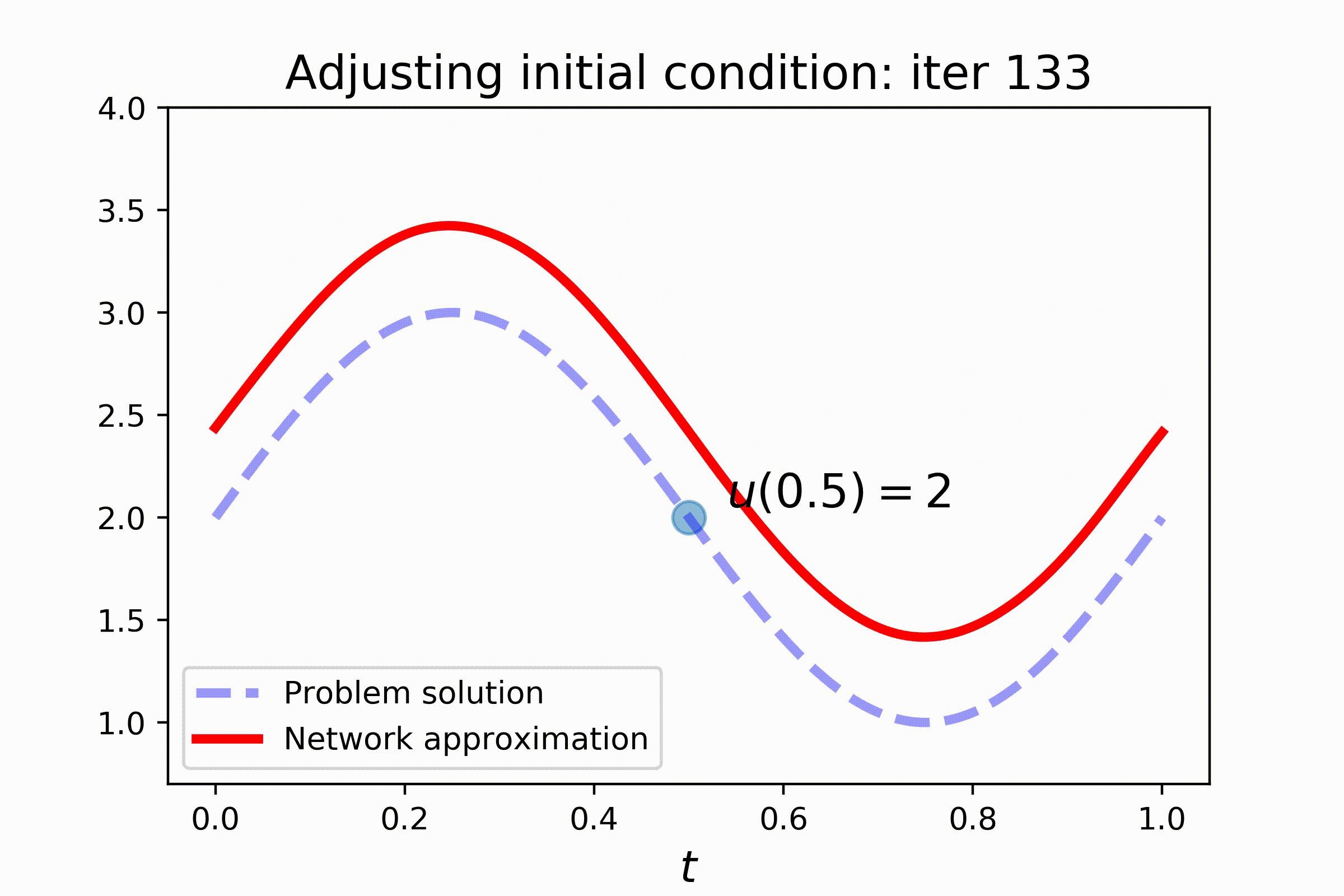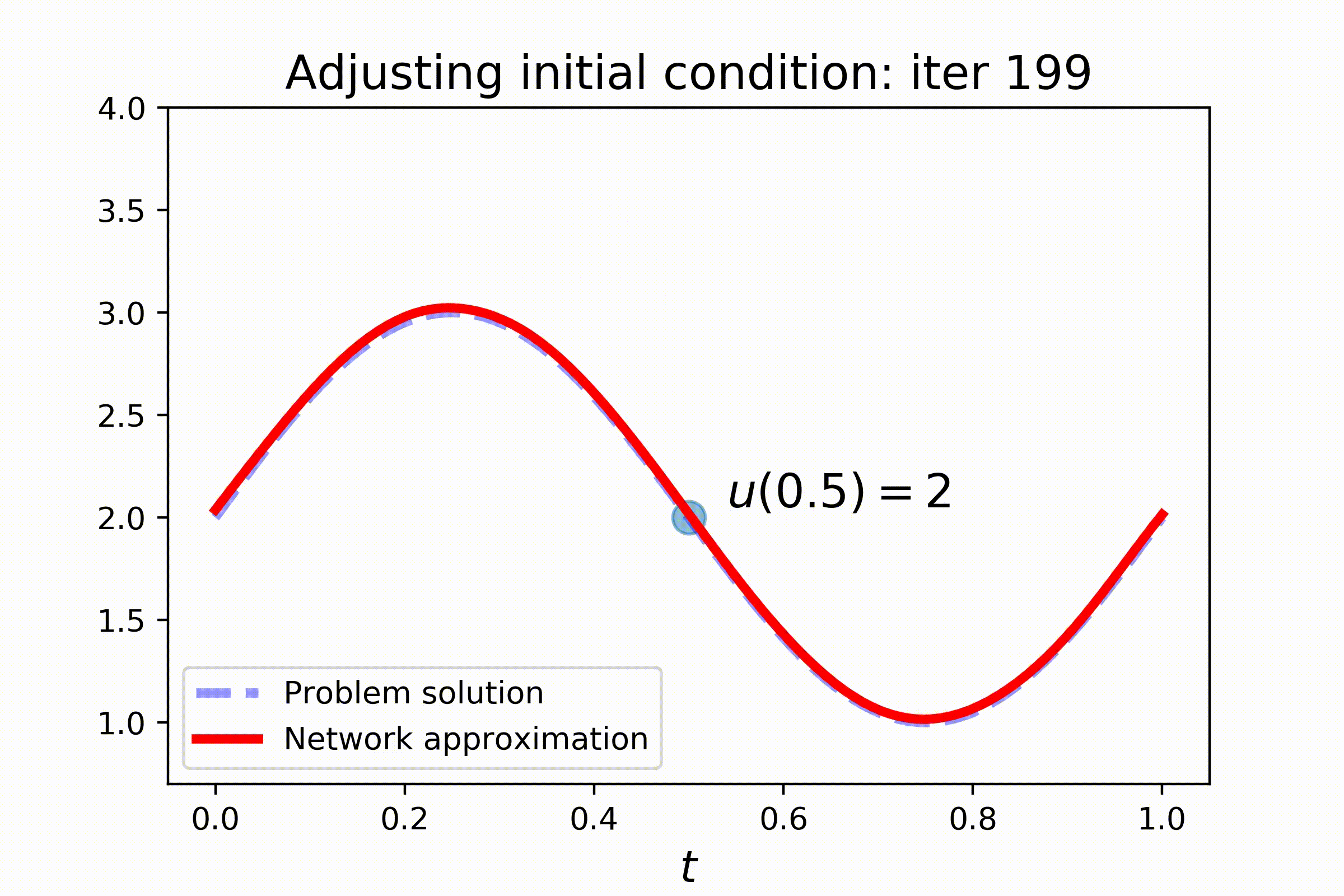
Setting this problem requires a slightly more complex configuring. Note the use of V-token, that stands for trainable variable, in the initial condition of the problem. Also pay attention to train_steps-key of the config, where two train steps are configured: one for better solving the equation and the other for satisfying the additional constraint:

pde = {'n_dims': 1,
       'form': lambda u, t: D(u, t) - 2 * np.pi * cos(2 * np.pi * t),
       'initial_condition': lambda: V(3.0)}

config = {'pde': pde,
          'track': {'u05': lambda u, t: u - 2},
          'train_steps': {'initial_condition_step': {'scope': 'addendums',
                                                     'loss': {'name': 'mse', 'predictions': 'u05'}},
                          'equation_step': {'scope': '-addendums'}}}

s1 = NumpySampler('uniform')
s2 = ConstantSampler(0.5)

Model-fitting comes in two parts now: (i) solving the equation and (ii) adjusting initial condition to satisfy the additional constraint:

dg.fit(batch_size=150, sampler=s1, n_iters=2000, train_mode='equation_step')
dg.fit(batch_size=150, sampler=s2, n_iters=2000, train_mode='initial_condition_step')

Check out the results:

Installation

First of all, you have to manually install tensorflow, as you might need a certain version or a specific build for CPU / GPU.

Stable python package

With modern pipenv

pipenv install pydens

With old-fashioned pip

pip3 install pydens

Development version

pipenv install git+https://github.com/analysiscenter/pydens.git

pip3 install git+https://github.com/analysiscenter/pydens.git

Installation as a project repository:

Do not forget to use the flag --recursive to make sure that BatchFlow submodule is also cloned.

git clone --recursive https://github.com/analysiscenter/pydens.git

In this case you need to manually install the dependencies.

Citing PyDEns

Please cite PyDEns if it helps your research.

Roman Khudorozhkov, Sergey Tsimfer, Alexander Koryagin. PyDEns framework for solving differential equations with deep learning. 2019.

@misc{pydens_2019,
  author       = {Khudorozhkov R. and Tsimfer S. and Koryagin. A.},
  title        = {PyDEns framework for solving differential equations with deep learning},
  year         = 2019
}

Runfa-Zhang/pydens