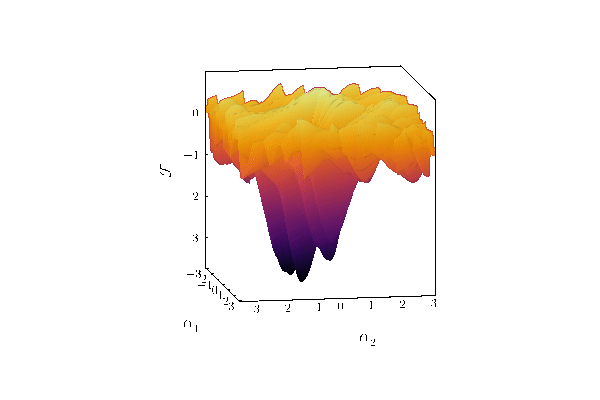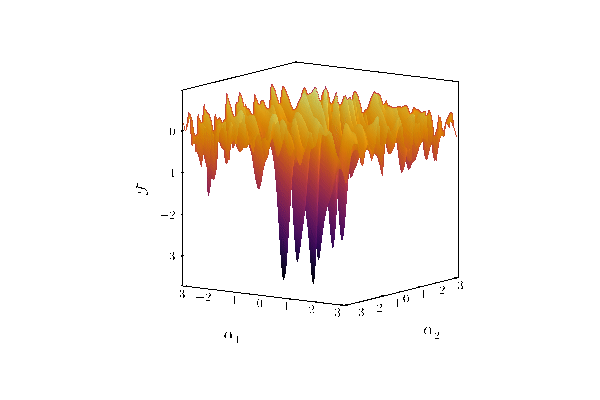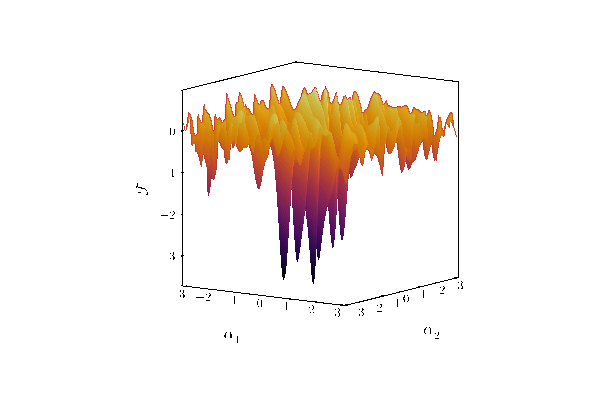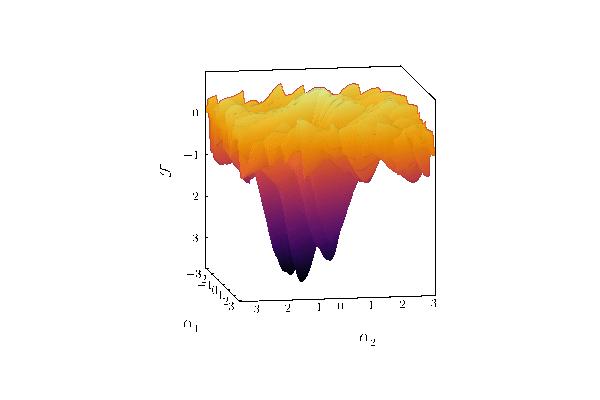Pulses.jl

Quantum optimal control made easy.

What is Quantum Optimal Control?

We go through life interacting with mechanisms that are controlled. For example, cruise control in a car will maintain a specific speed by appropriately applying fuel into the engine (or breaking). Of course, for the car to understand when it should apply fuel, it must have some feedback (closed-loop control)-- such as the speedometer. There are systems that do not need feedback (open-loop control), such as an electric clothes dryer that will continue operating for some time, regardless of clothes dryness.

Quantum systems, such as quantum computers, have parameters that we can control -- similar to the injection of fuel to a car engine, or the amount of heat to generate for an electric clothes dryer. The goal of quantum optimal control is to produce a desired operation (e.g. a quantum gate, or a quantum state) by computing pulses.

Why Pulses.jl?

There are already many quantum optimal control software packages out in the universe. Pulses.jl attempts to be tiny (under 100 lines of code!), while also being quite powerful. We achieve this by utilizing Julia and the Julia ecosystem, such as:

Zygote.jl for automatic differentiation
Optim.jl for multivariate optimization

Usage

] activate .
target = [...;...]
system = System(H_d, [H_c, ...])
initial_pulse = [...]
sol = Pulses.find_pulse(target, system, Δt, inital_pulse)

You may find more examples in examples.

Examples

Here are some examples and visualizations that were generated with Pulses.jl. The system Hamiltonians are taken to be superconducting Transmons.

Namely, the problem is the find pulses $\alpha(t)$ given a model of quantum device, whose Hamiltonian has the general form:

$$H(t) = H_d + \sum_i \alpha_i(t) H_{ci}$$ where $H_d$ is the drift Hamiltonian, and $H_c$ are Hamiltonians that interact with the system with come coupling $\alpha(t)$. The quantum gates are then solutions to the Schrödinger equation:

$$U(t_f, t_i) = \mathcal{T} \exp\left(-i \int_{t_i}^{t_f} H(t) dt\right).$$

The goal is to find $\alpha(t)$ such that $U$ is equal to our desired quantum gate.

Hadamard Gate (H)

We want the Hadamard gate, which in matrix form is:

$$H = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$$

Pulses.jl finds the minimum of this loss landscape:

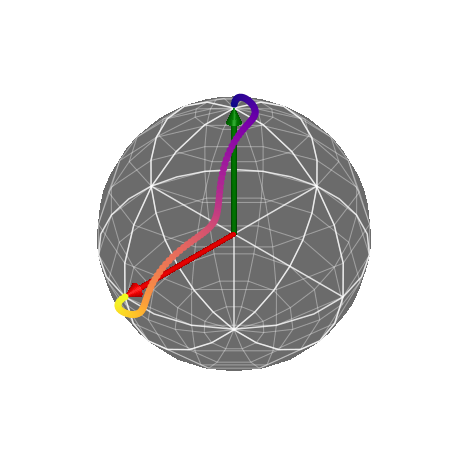
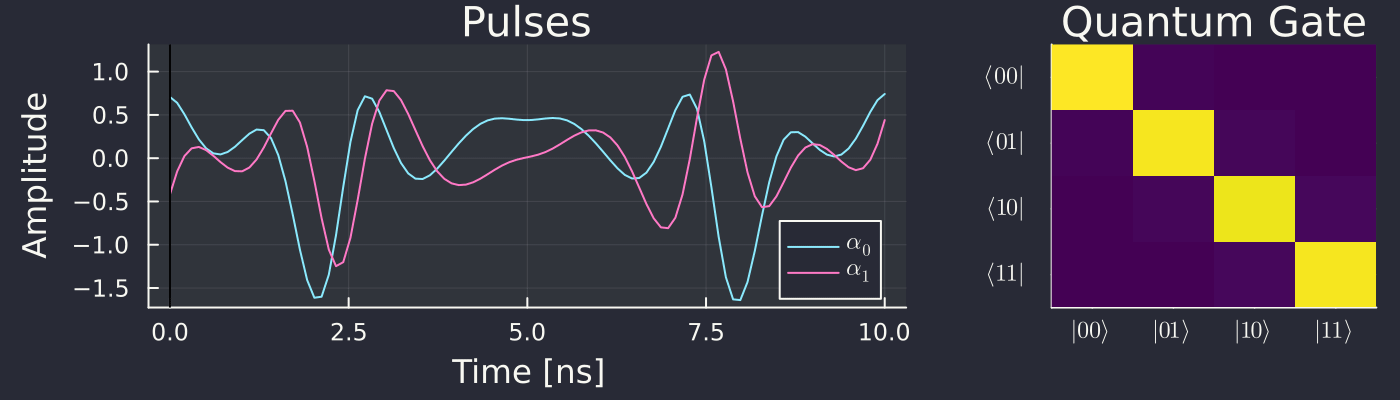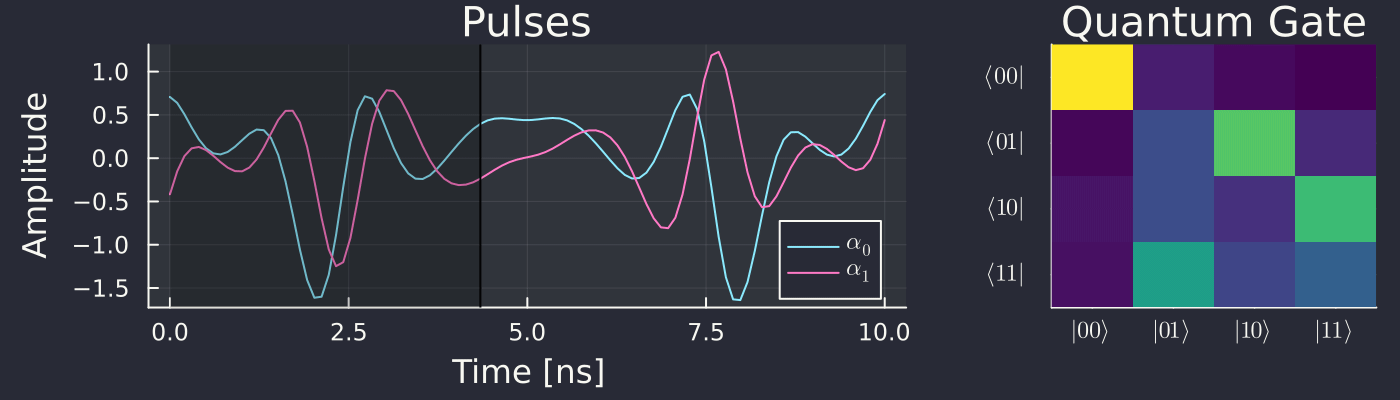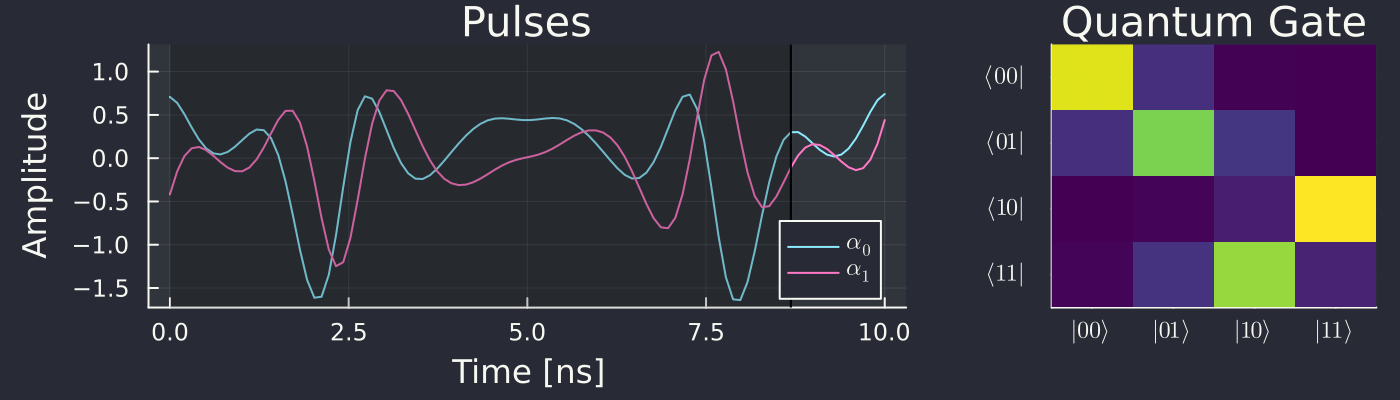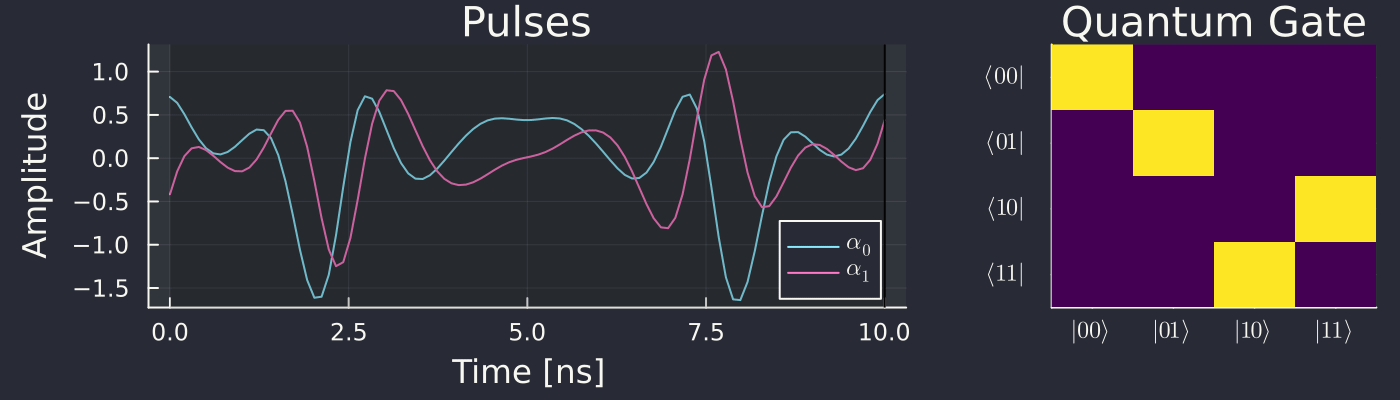
We then plot the found pulses, and also evolve a qubit in time using the pulses. Namely, starting in the state $\ket{0}$, we look at $\ket{\psi(t)} = U(t)\ket{0}$, where at final $t=T$, $\ket{\psi(T)} = H\ket{0} = \frac{1}{\sqrt{2}}\left(\ket{0} + \ket{1}\right)$.

Plot of $\ket{\psi(t)}$ on the Bloch sphere:

Controlled-NOT (CNOT)

We want the CNOT gate, which in matrix form is:

$$CNOT = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix}$$

Pulses.jl finds the minimum of this loss landscape:

We then plot the evolution of the gate $U(t)$ given the found pulses. At final moment in time $t=T$, the gate is indeed $U(T) = CNOT$.

How to cite

@software{Volya_Pulses_jl_A_tiny_2022,
    author = {Volya, Daniel},
    title = {{Pulses.jl: A tiny quantum optimal control library.}},
    month = {12},
    year = {2022},
    publisher = {Zenodo},
    url = {https://github.com/RustyBamboo/Pulses.jl},
}

License

Distributed under the MIT License. See LICENSE for more information.