DP-Knapsack

NTU SC2001 Example Class Project We have a knapsack of capacity weight $C$ (a positive integer) and $n$ types of objects.

Problem Statement

Each object of the ith type has weight $w_i$ and profit $p_i$ (all $w_i$ and all $p_i$ are positive integers, $i = 0, 1, …, n-1$).

There are unlimited supplies of each type of objects.

Find the largest total profit of any set of the objects that fits in the knapsack.

Let $P(C)$ be the maximum profit that can be made by packing objects into the knapsack of capacity $C$.

(1) Give a recursive definition of the function $P(C)$.

$P(C) = 0;\quad$ $\text{when } C = 0 \text{ or } n = 0$

$P(C) = max(P(C), P(C-weight[i])+P(i));\quad$ $\text{for } weight[i] < C$

$i:\text{any object available}$

(2) Draw the subproblem graph for $P(14)$ where n is 3 with the weights and profits given below.

	0	1	2
$W_i$	4	6	8
$P_i$	7	6	9

Fig1. Subproblem graph

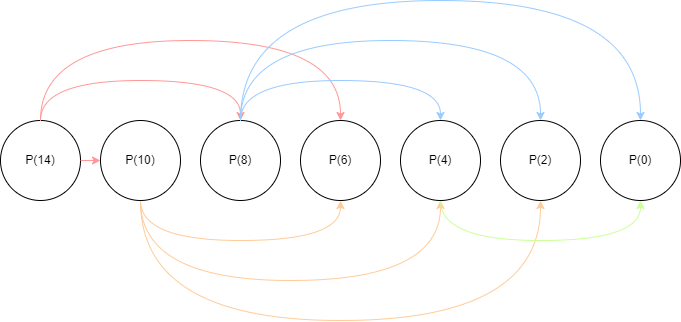
(3) Give a dynamic programming algorithm to compute the maximum profit, given a knapsack of capacity $C$, $n$ types of objects with weights $W_i$ and profits $P_i$ using the bottom up approach.

The algorithm:

Since we have unlimited objects for use, a simple $1D$ array can be used instead of a $2D$ array in the original Knapsack problem.

Each element in the array, namely dp[i] represents the maximum profit which can be stored in a knapsack of capacity i.

Following the recursive formula, we can construct the botton-up algorithm as following:

    dp[] = int[capacity+1];
    for(every object i < n){
        for(every capacity j < C){
            if w[i] <= j
                dp[j] = max(dp[j], p[i] + dp[j - W[i]])
        }
    }
    return dp[capacity]

Time complexity: $\Theta((W+1)*N)$. As we can take all items multiple number of times, we check all of them $(1\text{ to }N)$ for all weights from $0$ to $W$. Hence, $\text{time complexity} = (W+1) * N$

Space complexity: $\Theta(W+1)$. We maintain a dp array of size $W+1$, where $dp[i]$ denotes the maximum profit for capacity $i$. Hence, $\text{space complexity} = W+1$

(4) Code your algorithm in a programming language

a. show the running result of $P(14)$ with weights and profits given in (2).

b. Show the running result of $P(14)$ with weights and profits given below.

	0	1	2
$W_i$	5	6	8
$P_i$	7	6	9

see code

Ry3nG/Dp-Knapsack