This is a fast variant of the PyTorch GPT-2 trainer from Andrej Karpathy's llm.c repo, which attains the same final validation loss in:
- 2.4B tokens instead of 10B
- 10.8 minutes on 8xH100 instead of 45
It uses the following techniques:
- Modernized architecture: Rotary embeddings, QK-Norm, and ReLU^2.
- Projection layers initialized to zero (muP-like).
- Untied head from embedding and init to zero.
- New optimizer: Muon - Momentum Orthogonalized by Newton-schulz.
To execute the training, run the following three commands. They should all complete within <20min on an 8xH100 with decent internet connection.
pip install -r requirements.txt
python data/cached_fineweb10B.py 24 # downloads only the first 2.4B training tokens to save time
./run.shThe result will be a transformer with 124M active parameters trained for 4768 steps on 2.4B tokens of Fineweb [1], achieving ~3.275 validation loss. For comparison, the default llm.c PyTorch trainer yields >3.28 validation loss after training for 19560 steps on 10B tokens.
The following is the progression of world records for the task of training a model with 124M active parameters to 3.28 validation loss on FineWeb in the minimal amount of time on an 8xH100 machine.
- 45 minutes: llm.c baseline (05/28/24) [training log] (note: the 90 minute time is on 8xA100; it's 45 minutes on 8xH100)
- 31.4 minutes: Architectural modernizations and learning rate tuning (06/06/24) [training log] (note: this uses half the tokens as the baseline but isn't yet twice as fast since it's slower PyTorch code rather than raw CUDA. also note: by far the biggest improvement here came from simply tripling the learning rate.)
- 24.9 minutes: Introduced the Muon optimizer (10/04/24)
- 22.3 minutes: Muon improvements (10/11/24) [reproducible log]
- 15.2 minutes: Pad embeddings & architectural modernizations (10/14/24) [reproducible log]
- 13.1 minutes: Distributed the overhead of Muon (10/18/24) [reproducible log]
- 12.0 minutes: Upgraded PyTorch from 2.4.1 to 2.5.0 (10/18/24) [reproducible log] (note: this now runs at the same speed per step as the CUDA llm.c trainer!)
- 10.8 minutes: Untied embed and lm_head (11/03/24) [reproducible log]
Direct contributors to these records: @Grad62304977, @bozavlado, myself
Note: The original llm.c baseline is intended to be closer to a replication of GPT-2 than to an optimized LLM training. So it's no surprise that there is room to improve; as @karpathy has said, 'llm.c still has a lot of pending optimizations.' In addition, many of the techniques used in these records are completely standard, such as rotary embeddings. The goal of this benchmark/speedrun is simply to find out which techniques actually work, and maybe come up with some new ones.
A: Because it is a competitive benchmark. In particular, if you attain a new speed record (using whatever method you want), there is an open invitation for you to post that record (on arXiv or X) and thereby vacuum up all the clout for yourself. I will even help you do it by reposting you as much as I can.
Q: NanoGPT speedrunning is cool and all, but meh it probably won't scale and is just overfitting to val loss
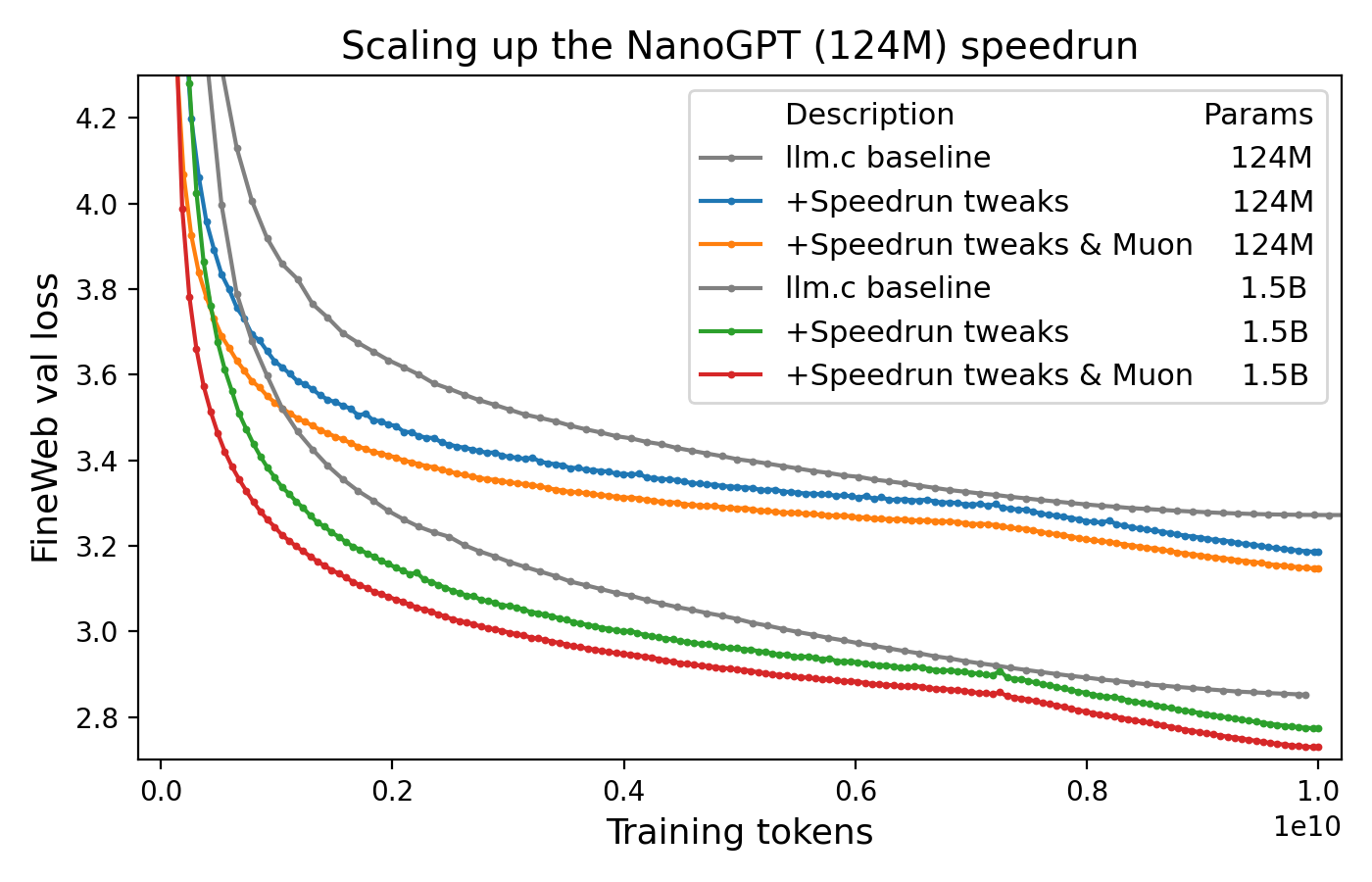
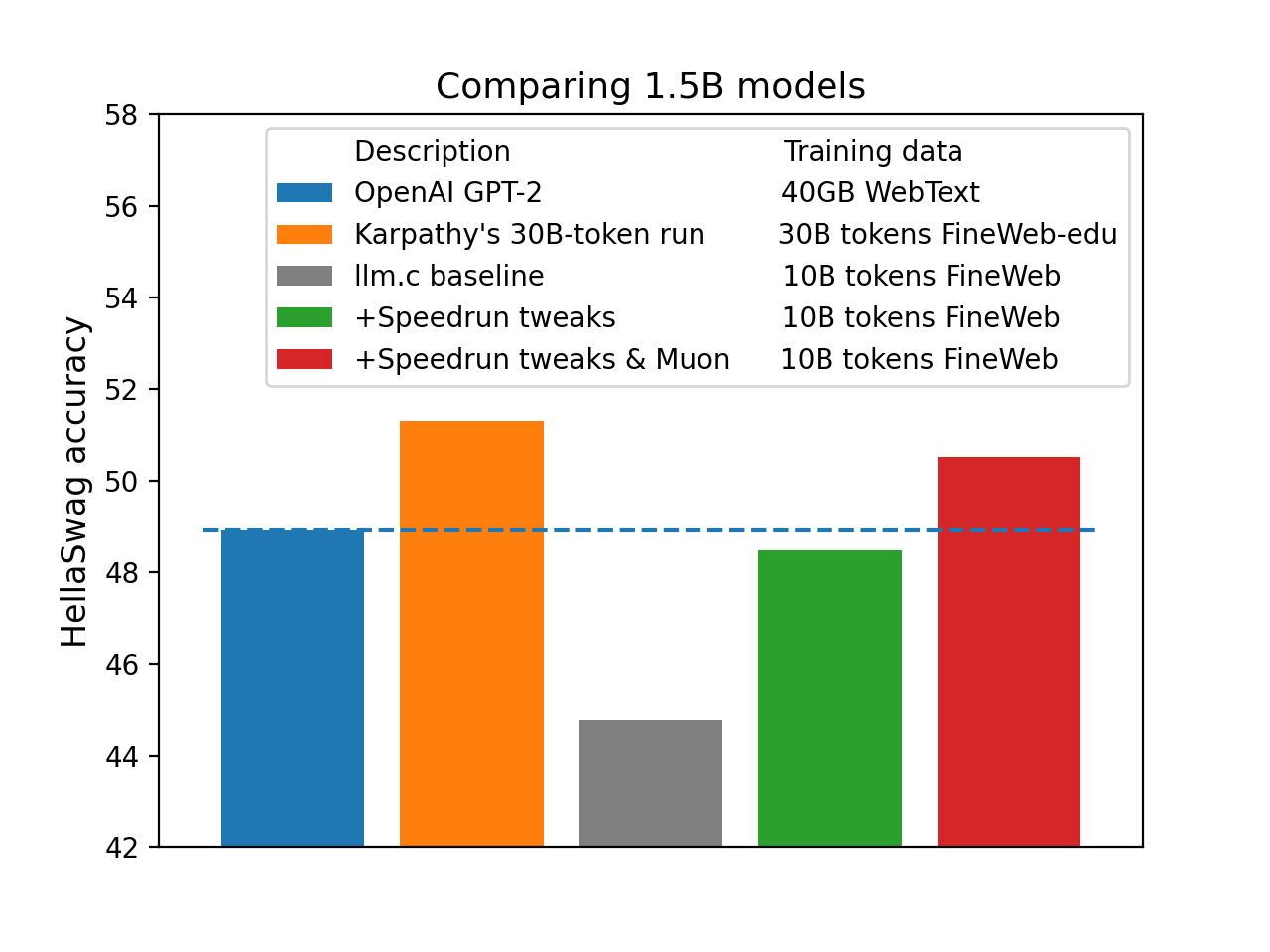
A: Ok, well, "at scale" is an infinite category (what if the methods stop working only for >100T models?), so it's impossible for me to conclusively refute the allegation that whatever we're doing here doesn't work at scale. But if you care about 1.5B models, then you might be convinced by this result:
Straightforwardly scaling up the speedrun to 1.5B parameters yields a model with GPT-2 (1.5B)-level quality 2.5x more cheaply than @karpathy's baseline ($233 instead of $576):
Muon is defined as follows:
Where NewtonSchulz5 is the following Newton-Schulz iteration [2, 3], which approximately replaces G with U @ V.T where U, S, V = G.svd().
@torch.compile
def zeroth_power_via_newtonschulz5(G, steps=5, eps=1e-7):
assert len(G.shape) == 2
a, b, c = (3.4445, -4.7750, 2.0315)
X = G.bfloat16() / (G.norm() + eps)
if G.size(0) > G.size(1):
X = X.T
for _ in range(steps):
A = X @ X.T
B = A @ X
X = a * X + b * B + c * A @ B
if G.size(0) > G.size(1):
X = X.T
return X.to(G.dtype)For this training scenario, Muon has the following favorable properties:
- Less memory usage than Adam
- ~1.5x faster training
- <2% wallclock overhead
Many of the choices made to generate this optimizer were obtained experimentally by our pursuit of CIFAR-10 speedrunning. In particular, we experimentally obtained the following practices:
- Using Nesterov momentum inside the update, with orthogonalization applied after momentum.
- Using a specifically quintic Newton-Schulz iteration as the method of orthogonalization.
- Using non-convergent coefficients for the quintic polynomial in order to maximize slope at zero, and thereby minimize the number of necessary Newton-Schulz iterations. It turns out that the variance doesn't actually matter that much, so we end up with a quintic that (rapidly) converges to the range 0.68, 1.13 upon repeated application, rather than to 1.
- Running the Newton-Schulz iteration in bfloat16 (whereas Shampoo implementations often compute the preconditioners via inverse-pth-roots in fp32 or fp64).
Our use of a Newton-Schulz iteration for orthogonalization traces to Bernstein & Newhouse (2024), who suggested it as a way to compute Shampoo [5, 6] preconditioners, and theoretically explored Shampoo without preconditioner accumulation. In particular, Jeremy Bernstein @jxbz sent us the draft, which caused us to experiment with various Newton-Schulz iterations as the orthogonalization method for this optimizer. If we had used SVD instead of a Newton-Schulz iteration, this optimizer would have been too slow to be useful. Bernstein & Newhouse also pointed out that Shampoo without preconditioner accumulation is equivalent to steepest descent in the spectral norm, and therefore Shampoo can be thought of as a way to smooth out spectral steepest descent. The proposed optimizer can be thought of as a second way of smoothing spectral steepest descent, with a different set of memory and runtime tradeoffs compared to Shampoo.
Here's a good startup script for a fresh instance. If you get torchrun not found after this upon running then just close and reopen your tmux tab.
sudo apt-get update
sudo apt-get install vim tmux python3-pip python-is-python3 -y
git clone https://github.com/KellerJordan/modded-nanogpt.git
cd modded-nanogpt
tmux
pip install numpy==1.23.5 huggingface-hub tqdm
pip install --upgrade torch &
python data/cached_fineweb10B.py 30
To run on fewer GPUs, just modify the 1-liner run.sh to have a different --nproc_per_node. If you don't have enough memory to fit the batch size, then
go into train_gpt2.py and scale down the device_batch_size by either 1/2 or 1/4.
Both of these changes will have no effect on the training - you should get the exact same loss curve as the most recent record, because the training code
will automatically adjust the gradient accumulation in order to have the same total batch size.
- Penedo, Guilherme, et al. "The fineweb datasets: Decanting the web for the finest text data at scale." arXiv preprint arXiv:2406.17557 (2024).
- Nicholas J. Higham. Functions of Matrices. Society for Industrial and Applied Mathematics, 2008. Equation 5.22.
- Günther Schulz. Iterative Berechnung der reziproken Matrix. Z. Angew. Math. Mech., 13:57–59, 1933.
- Jeremy Bernstein and Laker Newhouse. "Old Optimizer, New Norm: An Anthology." arxiv preprint arXiv:2409.20325 (2024).
- Vineet Gupta, Tomer Koren, and Yoram Singer. "Shampoo: Preconditioned stochastic tensor optimization." International Conference on Machine Learning. PMLR, 2018.
- Anil, Rohan, et al. "Scalable second order optimization for deep learning." arXiv preprint arXiv:2002.09018 (2020).
- Hägele, Alexander, et al. "Scaling Laws and Compute-Optimal Training Beyond Fixed Training Durations." arXiv preprint arXiv:2405.18392 (2024).