Chess is a strategical two player board game played on a 8x8 checkered board
where a player tries to capture opponent's king while protecting his own with the
help of 16 pieces and 6 types each of which has a unique set of possible moves.
- Download the repository as zip and extract it.
- Python should be installed on the system.
- Open command prompt in the extracted folder.
- Run this command:
pip install -r requirements.txt - Run the game with this command:
python game.py - Choose game mode from command prompt.
- Enjoy !!🙂
Engine keeps track of the turn and if that player selects a piece, all the valid
moves of that piece are highlighted and if square is selected among those,
the move is played and turn switches to other player. Game ends when the
player in turn has no valid moves left.
All the moves of opponent's pieces are generated and if any of the piece
is attacking the king, the current player is in check.
All possible moves of selected piece are generated.
- If the king is in check and a move doesn't prevent it, it is not valid.
- If the king is not in check, but a move causes check, it is not valid.
Player is given option to choose it's preferred color.
After player has made the move, computer generates a move for it's color.
The move is played and waits for next player move.
There are several versions which have differnet ways of generating moves:
- Random Move Generator: All the pieces are iterated one by one if the piece
has any valid move. A random number is generated. If the number is greater
than the threshold, that piece is selected to make the move and a random move
among the valid moves is made. - Greedy Move Generator: The move which results in capturing highest scored
piece from opponent immediately is selected. If no move results in capturing,
a random move is selected. - Minimax Algorithm: Minimax is extended version of greedy algorithm where
instead for each move of one player all moves of opponent are generated and so
on and best score among all cases is selected. This algorithm is based on
backtracking.
Assumptions
We will take a state of board and calculate the score of current position.
Let's assume that a positive score is favorable for white and negative
score favors black. So, a white player will try to move pieces in a way
which allows him to increase the score of board. For now, we assume we have
a function to calculate the score from board.
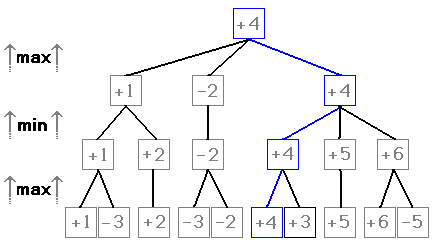
Min Max Tree
We consider the state of board generated by each move as a child node of
previous state of board. After one move, the turn switches so next layer
will consider all opponents moves and so on. Once we reach desired depth
we calculate the score of all the leaf node boards.
We assume that both players play optimally. If the turn at leaf node is
white's, we will take the maximum of all child nodes and assign it to
parent nodes as white is trying to maximise the score. Among all the parent
nodes, we take the minimum and assign it to their parents because turn
switches and black tries to minimise the score. The final score of root node
is the best score the player can get from current state of board and the
move is made to achieve that score.
An example of simple game tree:
Efficiency of algorithm
The maximum number of moves a piece has is 32(Queen on centre) and other
pieces have 3-16 moves. So the number of leaf nodes increase exponentially
as we try to increase the number of layers. For a depth of 2, on average
there are 4000 leaf nodes and for depth 3, there are 25000 leaf nodes and
calculating the score will require some calculations and doing that for
each leaf node is inefficient, so it's not feasible to go beyond 3 layers
without any optimizations.
Alpha beta pruning
In alpha beta pruning, we avoid searching the branches that will not yield
the optimal score in any case.
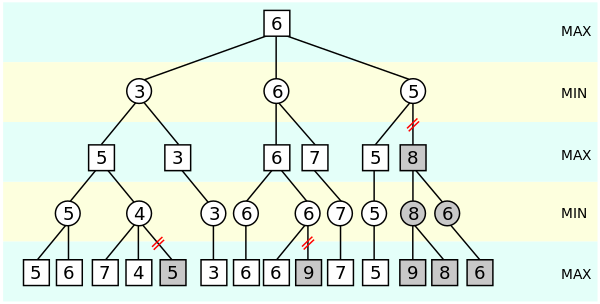
In this tree, consider the rightmost subtree. The score of one subtree is 5.
We already have a score of 6 from middle subtree which is greater than 5.
If the rest of subtree in rightmost branch gives a score of greater than 5,
it will not be considered as this is opponent's turn and it will minimize the
score. If it is less than 6, then also it will not be considered as it is
not optimal. So we don't need to calculate the tree at all which decreases the
number of leaves evaluated.
Observed efficiency after using alpha beta pruning, for a depth of 2, only
500 leaf nodes are evaluated and for depth of 3, 5000 leaf nodes are evaluated
which is a significant improvement. The number of nodes evaluated depends on
the evaluation of score. With a better evaluation function, we can further
reduce the nodes evaluated by a great amount.
Evaluation function
Each piece has a base score associated with it. In a game of chess, pawn is
worth 1 point, bishop and knight are worth 3 points, rook is worth 5 point and
queen is worth 9 points. We can assign scores to pieces similar to this basis.
But, just the piece itself is not an appropriate measure. The position of
piece also matters. I have added piece tables which grants bonus points if
a certain type of piece is on a strong square, thus motivating the computer
to make certain moves thus improving the structure. The number of valid moves
is also considered a factor as a piece free to move is stronger than a trapped
piece. If a piece is defending other pieces or attacking other pieces, it is
stronger which is also taken into account.
We can tweak the points awarded for each of these parameters and add other
factors to make a better evaluation function.