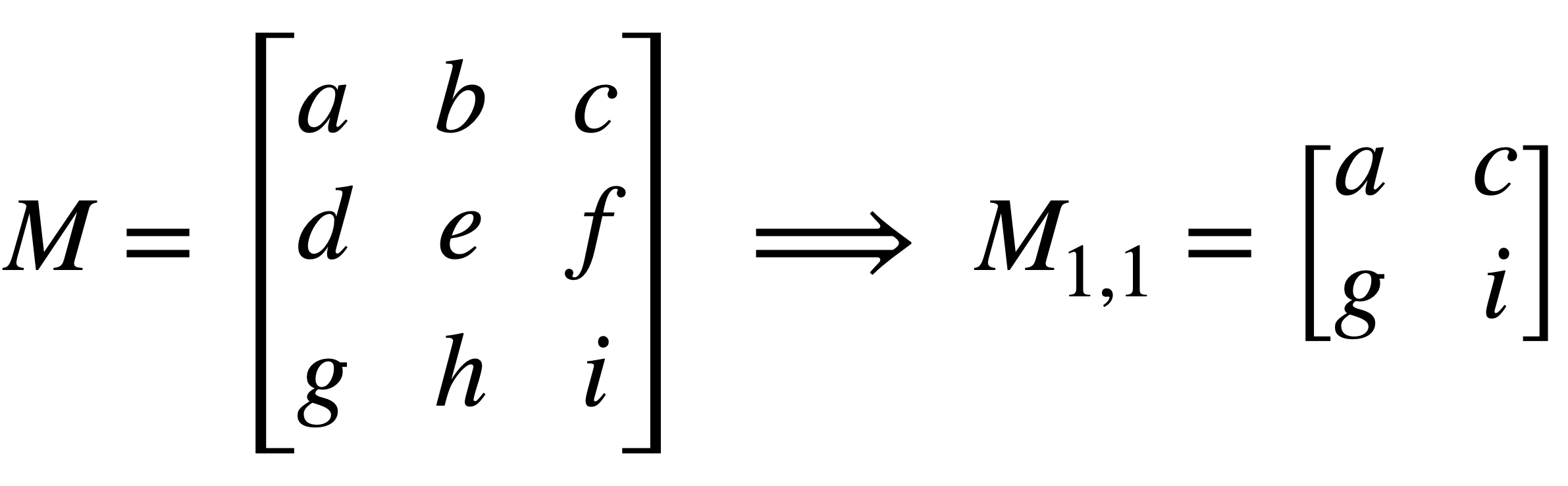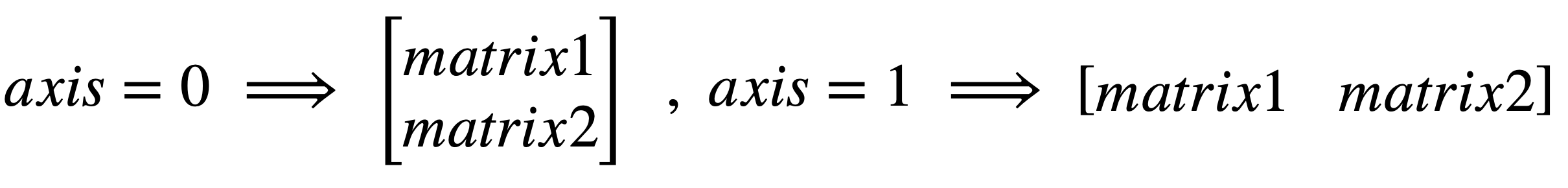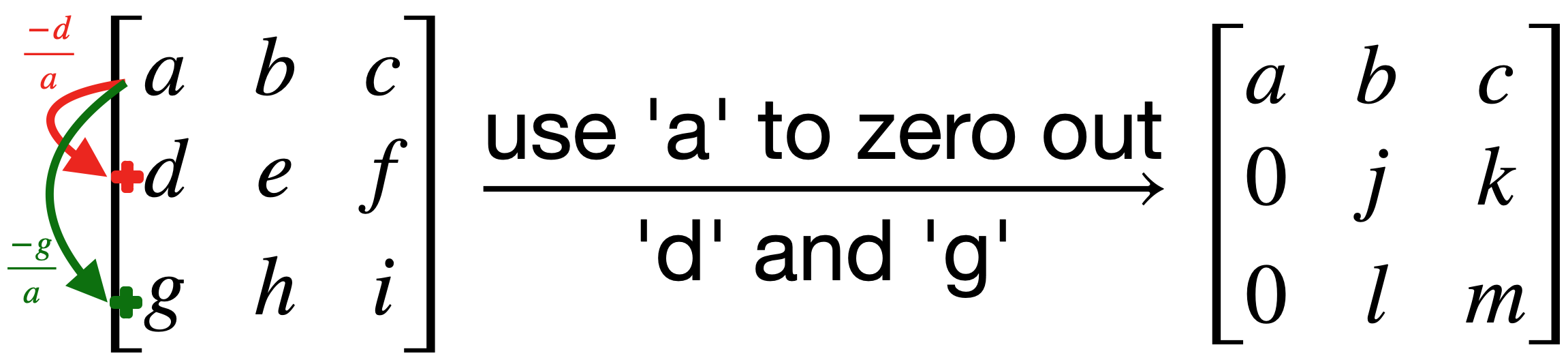In this homework we are going to implement a Linear Algebra library for c++.
In this library we are going to implement different functions to allow our users to easilly work and manipulate different matrices.
We will be implementing all our functions in hw1.cpp and hw1.h. remember you should put all declarations in the .h and all the implementations in the .cpp file.
In order to have a matrix in c++ we need a 2D vector. We use the following line in order to reduce our syntax.
using Matrix = std::vector<std::vector<double>>;From now on we can use the keyword Matrix instead of defining the 2D vector everytime. So, go ahead and put the above line in your code.
note. Define all your functions in a namespace called algebra.
Now, lets discuss each functions and see how they should be implemented.
-
zeros implement this function so that it will create a
n x mmatrix with all elements equal to zero.Matrix zeros(size_t n, size_t m)
-
ones implement this function so that it will create a
n x mmatrix with all elements equal to one.Matrix ones(size_t n, size_t m)
-
random implement this function so that it will create a
n x mmatrix with all elements a random number betweenminandmax.Matrix random(size_t n, size_t m, double min, double max)
note. to generate a random number you are not allowed to use
randandsrandfunctions. instead, use the<random>library first introduced in c++11. -
show implement this function so that it will display the matrix in a beautiful way.
void show(const Matrix& matrix)
note. to display your matrices use the
<iomanip>library. when showing the numbers, each element of the matrix should have exactly 3 decimal places. -
multiply - scalar number
implement this function so that it multiplies the
matrixinto the constant scalarc.Matrix multiply(const Matrix& matrix, double c)
-
multiply - matrix
implement this function so that it multiplies the
matrix1intomatrix2. (this is not an element-wise multiplication)Matrix multiply(const Matrix& matrix1, const Matrix& matrix2)
-
sum - scalar number
implement this function so that it adds the constant number
cto every element ofmatrix.Matrix sum(const Matrix& matrix, double c)
-
sum - matrix
implement this function so that it adds 2 matrices to each other.
Matrix sum(const Matrix& matrix1, const Matrix& matrix2)
-
transpose implement this function so that it will generate the transpose matrix of the input
matrix.Matrix transpose(const Matrix& matrix)
-
minor implement this function so that it will create the minor of the input
matrixwith respect to nth row and mth column.Matrix minor(const Matrix& matrix, size_t n, size_t m)
note. the indices in c++ start from 0
not 1, for example:
-
determinant implement this function so that it calculates the determinant of the input
matrix.double determinant(const Matrix& matrix)
you should only use the minor approach to calculate the determinant, any other methods (such as upper-triangular or ...) is not allowed.
-
inverse implement this function so that it generates the
matrix's inverse.Matrix inverse(const Matrix& matrix)
-
concatenate implement this function so that it will concatenate
matrix1andmatrix2along the specified axis. (axis=0: on top of each other |axis=1: alongside each other).Matrix concatenate(const Matrix& matrix1, const Matrix& matrix2, int axis=0)
-
elementary row operations we want to implement elementary row operation (ERO) functionality for our library. as you know we have 3 EROs:
1)swapping two rows.2)multiplying a row into a constant number.3)multiplying a row into a constant number and add it to another row.So, lets define the following 3 functions to do this.
-
swap swaps r1th row with r2th.
Matrix ero_swap(const Matrix& matrix, size_t r1, size_t r2)
-
multiply multiplies every element in rth row with constant number
c.Matrix ero_multiply(const Matrix& matrix, size_t r, double c)
-
sum adds r1th x c into r2th row.
Matrix ero_sum(const Matrix& matrix, size_t r1, double c, size_t r2)
-
-
upper triangular implement this function so that it will calculate the upper triangular form of the
matrixusing the ERO operations.Matrix upper_triangular(const Matrix& matrix)
note. to make a upper triangular matrix you have to zero out all the elements which are below the main diagonal, using the elemnts on the main diagonal. consider the following example:
use the same trick to zero out
l, usingjlike the following.
bonus question what happens if we come across a zero on our main diagonal for example
aorjin the example above? solve this problem.The last unit-test is for the bonus question. don't worry too much if it fails.
- Whenever you are defining a function you should always consider every aspect of its usage. in this homework you are writing a library, so it can be used by others. so you should keep in mind they may not always use your functions properly. for example, they may try to calculate the invert of a non-singular matrix, or they may try to multiply two matrices with incorrect dimensions.
You should keep track of these misbehaviours that may happen in your functions and throw a
logic errorin these cases. if you are not familiar of how to throw errors just try to google it. don't worry it will be the simplest part of the homework 😜 - other than logic errors you should consider that the users may try to use empty matrices with your functions. (for example the determinant of an empty matrix is 1). keep this in mind in all your implementations.
As mentioned before, keep all your implementations in hw1.cpp and hw1.h. do not alter other files at all. In case you want to test your code you may only use the debug section of the main.cpp which will be explained in the TA class.
if (true) // make false to run unit tests
{
// debug section
}
else
{
::testing::InitGoogleTest(&argc, argv);
std::cout << "RUNNING TESTS ..." << std::endl;
int ret{RUN_ALL_TESTS()};
if (!ret)
std::cout << "<<<SUCCESS>>>" << std::endl;
else
std::cout << "FAILED" << std::endl;
}
return 0;GOOD LUCK