BayesRepDesign is an R package for Bayesian sample size calculation for replication studies. For information on the statistical framework underlying the package, have a look at the paper
Pawel, S., Consonni, G., Held, L. (2023). Bayesian approaches to designing replication studies. Psychological Methods. DOI:10.1037/met0000604
## development version from GitHub
remotes::install_github(repo = "SamCH93/BayesRepDesign")
## CRAN version
install.packages("BayesRepDesign")library("BayesRepDesign")
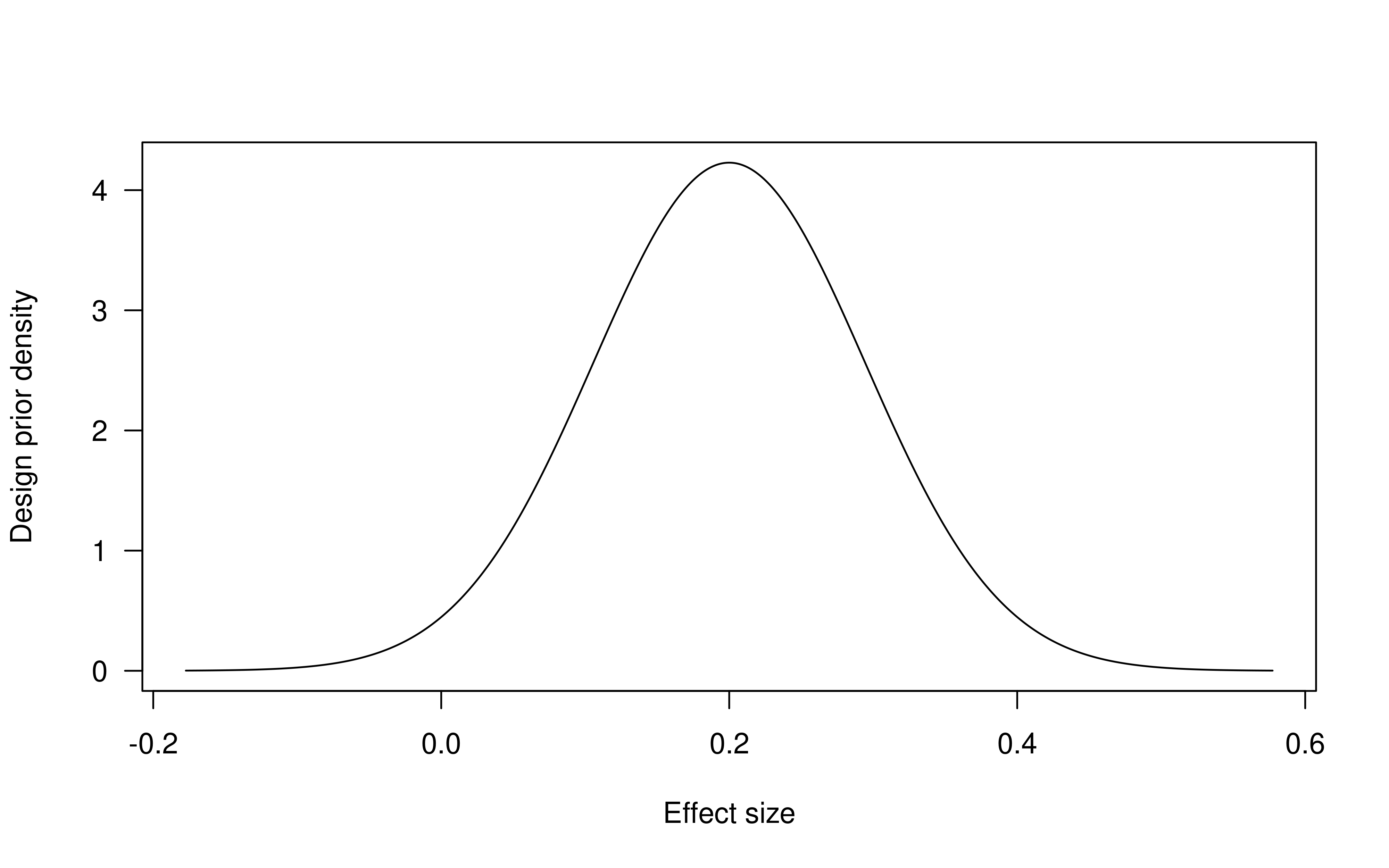
## design prior (flat initial prior for effect size + heterogeneity)
dp <- designPrior(to = 0.2, so = 0.05, tau = 0.08)
plot(dp)
## compute replication standard error for achieving significance at 2.5%
ssdSig(level = 0.025, dprior = dp, power = 0.8)
#> Bayesian sample size calculation for replication studies
#> ========================================================
#>
#> success criterion and computation
#> ------------------------------------------------------------------------
#> replication p-value <= 0.025 (exact computation)
#>
#> original data and initial prior for effect size
#> ------------------------------------------------------------------------
#> to = 0.2 : original effect estimate
#> so = 0.05 : standard error of original effect estimate
#> tau = 0.08 : assumed heterogeneity standard deviation
#> N(mean = 0, sd = Inf) : initial normal prior
#>
#> design prior for effect size
#> ------------------------------------------------------------------------
#> N(mean = 0.2, sd = 0.094) : normal design prior
#>
#> probability of replication success
#> ------------------------------------------------------------------------
#> PoRS = 0.8 : specified
#> PoRS = 0.8 : recomputed with sr
#>
#> required sample size
#> ------------------------------------------------------------------------
#> sr = 0.045 : required standard error of replication effect estimate
#> c = so^2/sr^2 ~= nr/no = 1.2 : required relative variance / sample size
## compute numerically via success region and method agnostic function
sregFun <- function(sr) {
## success region is [1.96*sr, Inf)
successRegion(intervals = cbind(qnorm(p = 0.975)*sr, Inf))
}
ssd(sregionfun = sregFun, dprior = dp, power = 0.8)
#> Bayesian sample size calculation for replication studies
#> ========================================================
#>
#> success criterion and computation
#> ------------------------------------------------------------------------
#> method agnostic success region (numerical computation)
#>
#> original data and initial prior for effect size
#> ------------------------------------------------------------------------
#> to = 0.2 : original effect estimate
#> so = 0.05 : standard error of original effect estimate
#> tau = 0.08 : assumed heterogeneity standard deviation
#> N(mean = 0, sd = Inf) : initial normal prior
#>
#> design prior for effect size
#> ------------------------------------------------------------------------
#> N(mean = 0.2, sd = 0.094) : normal design prior
#>
#> probability of replication success
#> ------------------------------------------------------------------------
#> PoRS = 0.8 : specified
#> PoRS = 0.8 : recomputed with sr
#>
#> required sample size
#> ------------------------------------------------------------------------
#> sr = 0.045 : required standard error of replication effect estimate
#> c = so^2/sr^2 ~= nr/no = 1.2 : required relative variance / sample size