Comparación de Métodos Estocásticos de estimación de IBNR

Este repositorio contiene una librería que estima los IBNR por el método Chain-Ladder de manera determinística y cinco metodologías para hacerlo de manera estocástica:

Mack (1993)
Bootstrap paramétrico normal
Boostrap paramétrico t
Boostrap no parmétrico
Boostrap no paramétrico suavizado

Además, en el presente MARKDOWN se implementa la librería para comparar los resultados arrojados por los cinco métodos previamente mencionados.

Carga de datos

# Cargar librerías
import IBNR
import numpy as np
import pandas as pd
import scipy.stats as st
import matplotlib.pyplot as plt

# Triángulo  - Tabla 1: Mack (1993) https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=c449e39e64fd29b9aac7dd9266b841aa7ebc17ac

tab1 = [
[357848, 1124788, 1735330, 2218270, 2745596, 3319994, 3466336, 3606286, 3833515, 3901463],
[352118, 1236139, 2170033, 3353322, 3799067, 4120063, 4647867, 4914039, 5339085, 0],
[290507, 1292306, 2218525, 3235179, 3985995, 4132918, 4628910, 4909315, 0, 0],
[310608, 1418858, 2195047, 3757447, 4029929, 4381982, 4588268, 0, 0, 0],
[443160, 1136350, 2128333, 2897821, 3402672, 3873311, 0, 0, 0, 0],
[396132, 1333217, 2180715, 2985752, 3691712, 0, 0, 0, 0, 0],
[440832, 1288463, 2419861, 3483130, 0, 0, 0, 0, 0, 0],
[359480, 1421128, 2864498, 0, 0, 0, 0, 0, 0, 0],
[376686, 1363294, 0, 0, 0, 0, 0, 0, 0, 0],
[344014, 0, 0, 0, 0, 0, 0, 0, 0, 0]
]

# Crear objeto
tr_acumulado = IBNR.Triangulo(triangulo = np.array(tab1),
                              años_desarrollo=range(1,11),
                              años_siniestro=range(1,11),tipo='Conteos')

tr = tr_acumulado.desacumular() # Desacumular triángulo original
tr

Año Desarrollo      1        2        3        4       5       6       7   \
Año Siniestro                                                               
1               357848   766940   610542   482940  527326  574398  146342   
2               352118   884021   933894  1183289  445745  320996  527804   
3               290507  1001799   926219  1016654  750816  146923  495992   
4               310608  1108250   776189  1562400  272482  352053  206286   
5               443160   693190   991983   769488  504851  470639       0   
6               396132   937085   847498   805037  705960       0       0   
7               440832   847631  1131398  1063269       0       0       0   
8               359480  1061648  1443370        0       0       0       0   
9               376686   986608        0        0       0       0       0   
10              344014        0        0        0       0       0       0   

Año Desarrollo      8       9      10  
Año Siniestro                          
1               139950  227229  67948  
2               266172  425046      0  
3               280405       0      0  
4                    0       0      0  
5                    0       0      0  
6                    0       0      0  
7                    0       0      0  
8                    0       0      0  
9                    0       0      0  
10                   0       0      0

# Aplicar funciones a los valores del triángulo
tr.apply(np.log)

C:\Users\SHSANCHE\OneDrive - Proteccion S.A\Procesos Actuaría\Practicante\2023-01\Proyecto IBNR\IBNR\s02_crear_triangulos.py:152: RuntimeWarning: divide by zero encountered in log





Año Desarrollo         1          2          3          4          5   \
Año Siniestro                                                           
1               12.787864  13.550164  13.322102  13.087648  13.175574   
2               12.771722  13.692236  13.747118  13.983808  13.007502   
3               12.579383  13.817308  13.738866  13.832027  13.528916   
4               12.646287  13.918293  13.562151  14.261734  12.515328   
5               13.001686  13.449059  13.807461  13.553481  13.132019   
6               12.889503  13.750529  13.650044  13.598644  13.467314   
7               12.996419  13.650201  13.938965  13.876859   0.000000   
8               12.792414  13.875333  14.182491   0.000000   0.000000   
9               12.839167  13.802028   0.000000   0.000000   0.000000   
10              12.748438   0.000000   0.000000   0.000000   0.000000   

Año Desarrollo         6          7          8          9          10  
Año Siniestro                                                          
1               13.261078  11.893702  11.849040  12.333714  11.126498  
2               12.679184  13.176480  12.491898  12.959953   0.000000  
3               11.897664  13.114315  12.543990   0.000000   0.000000  
4               12.771537  12.237019   0.000000   0.000000   0.000000  
5               13.061847   0.000000   0.000000   0.000000   0.000000  
6                0.000000   0.000000   0.000000   0.000000   0.000000  
7                0.000000   0.000000   0.000000   0.000000   0.000000  
8                0.000000   0.000000   0.000000   0.000000   0.000000  
9                0.000000   0.000000   0.000000   0.000000   0.000000  
10               0.000000   0.000000   0.000000   0.000000   0.000000

# Exportar a Excel
tr.to_excel('triangulo_acumulado_mack_1993.xlsx')

# Exportar a LaTeX
print(tr.df.to_latex())

\begin{tabular}{lrrrrrrrrrr}
\toprule
Año Desarrollo & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
Año Siniestro &  &  &  &  &  &  &  &  &  &  \\
\midrule
1 & 357848 & 766940 & 610542 & 482940 & 527326 & 574398 & 146342 & 139950 & 227229 & 67948 \\
2 & 352118 & 884021 & 933894 & 1183289 & 445745 & 320996 & 527804 & 266172 & 425046 & 0 \\
3 & 290507 & 1001799 & 926219 & 1016654 & 750816 & 146923 & 495992 & 280405 & 0 & 0 \\
4 & 310608 & 1108250 & 776189 & 1562400 & 272482 & 352053 & 206286 & 0 & 0 & 0 \\
5 & 443160 & 693190 & 991983 & 769488 & 504851 & 470639 & 0 & 0 & 0 & 0 \\
6 & 396132 & 937085 & 847498 & 805037 & 705960 & 0 & 0 & 0 & 0 & 0 \\
7 & 440832 & 847631 & 1131398 & 1063269 & 0 & 0 & 0 & 0 & 0 & 0 \\
8 & 359480 & 1061648 & 1443370 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
9 & 376686 & 986608 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
10 & 344014 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\bottomrule
\end{tabular}

Gráficos descriptivos

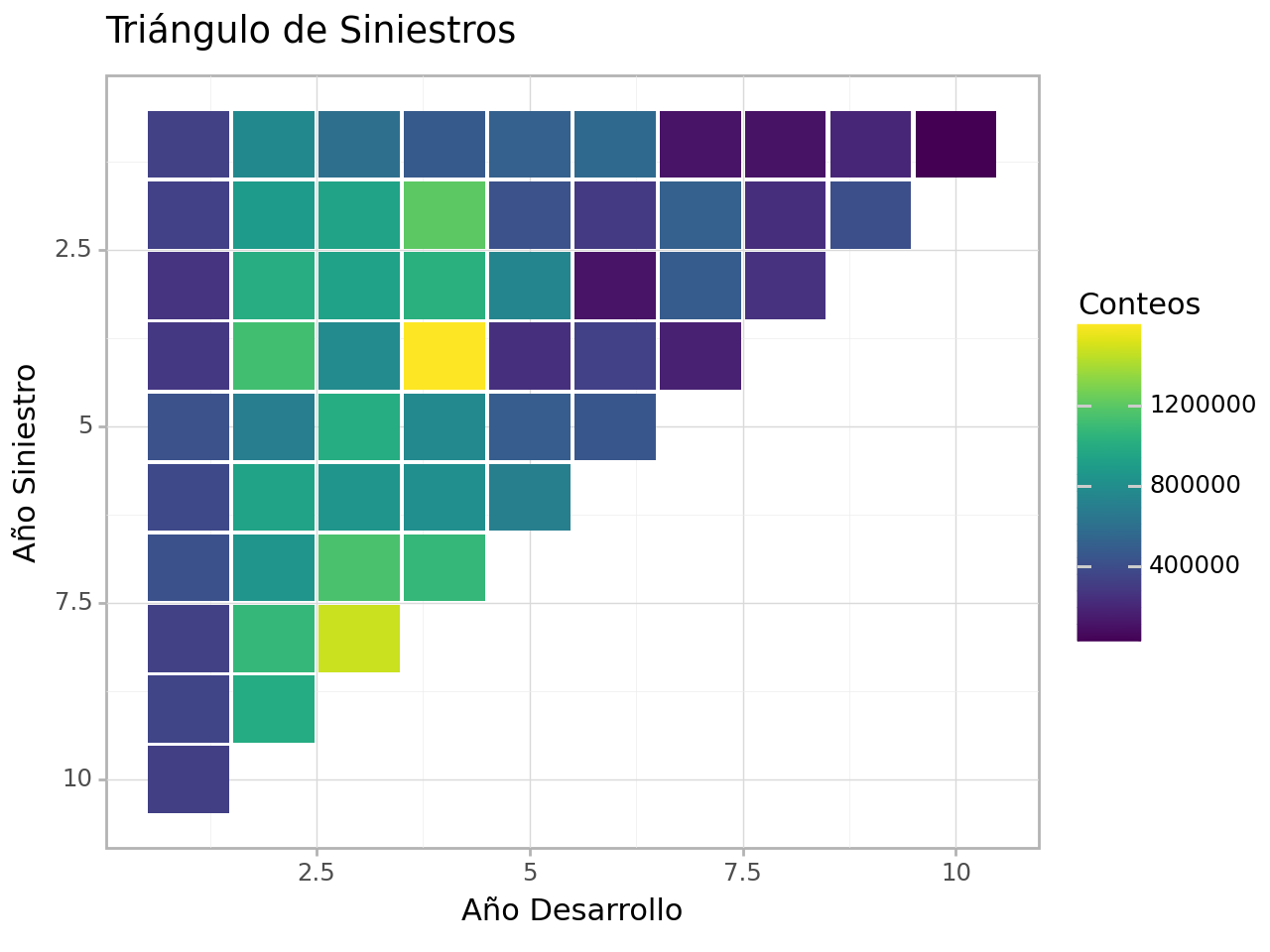
# Triángulo representado por medio de un mapa de calor
tr.heat_plot()

<Figure Size: (640 x 480)>

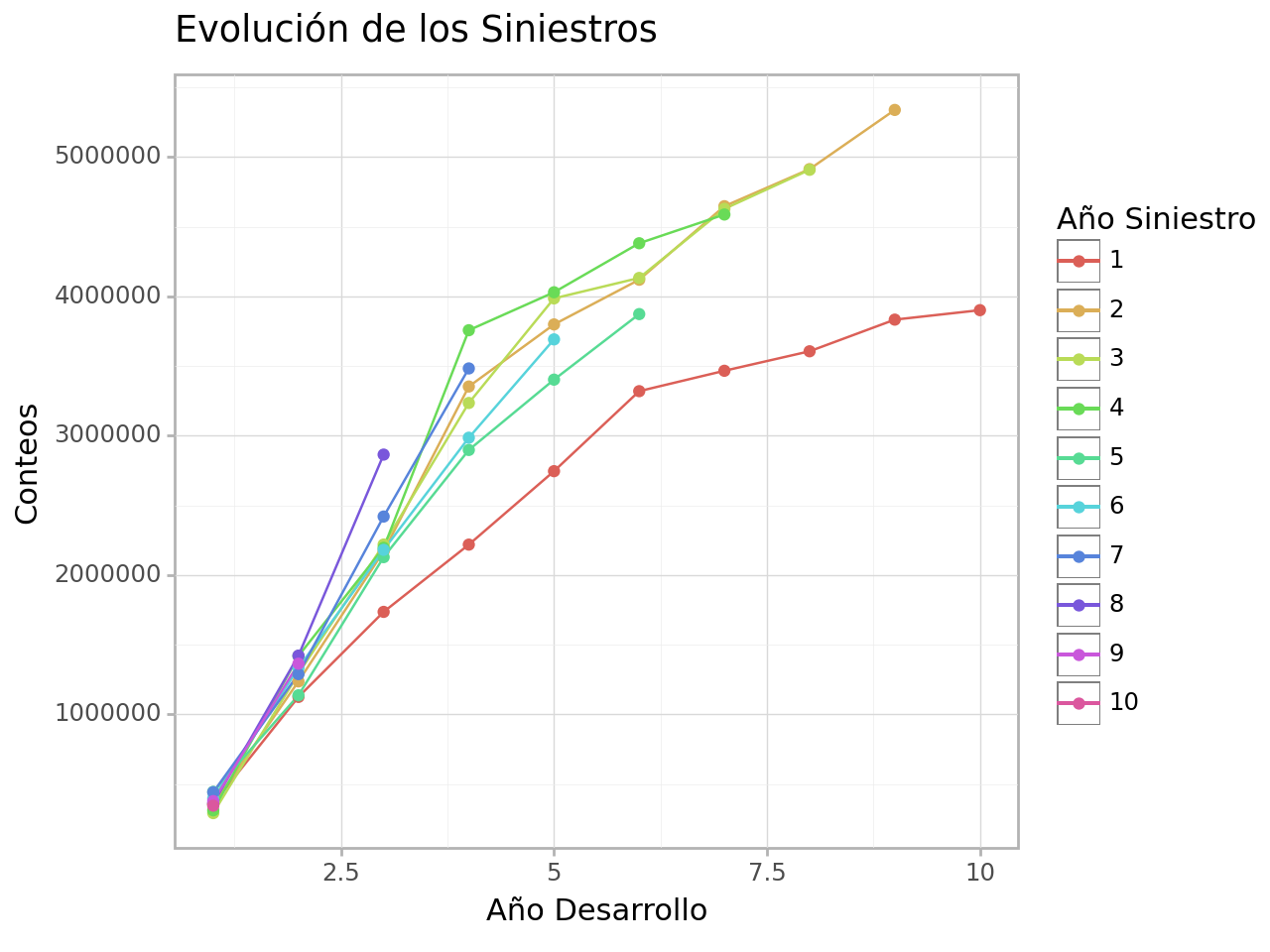
# Cantidad de siniestros reportados por año según el año de origen
tr.acumular().line_plot()

<Figure Size: (640 x 480)>

Chain-Ladder

# Factores de desarrollo
tr.factores_desarrollo()

[3.4906065479322863,
 1.7473326421004893,
 1.4574128360182361,
 1.1738517093997867,
 1.103823532244344,
 1.0862693644363943,
 1.0538743555048127,
 1.0765551783529383,
 1.017724725219544]

# Varianzas
tr.varianzas()

[160280.32748048689,
 37736.855047996374,
 41965.21301742404,
 15182.902680976436,
 13731.323891978891,
 8185.771620009633,
 446.616550105352,
 1147.3659684286617,
 446.616550105352]

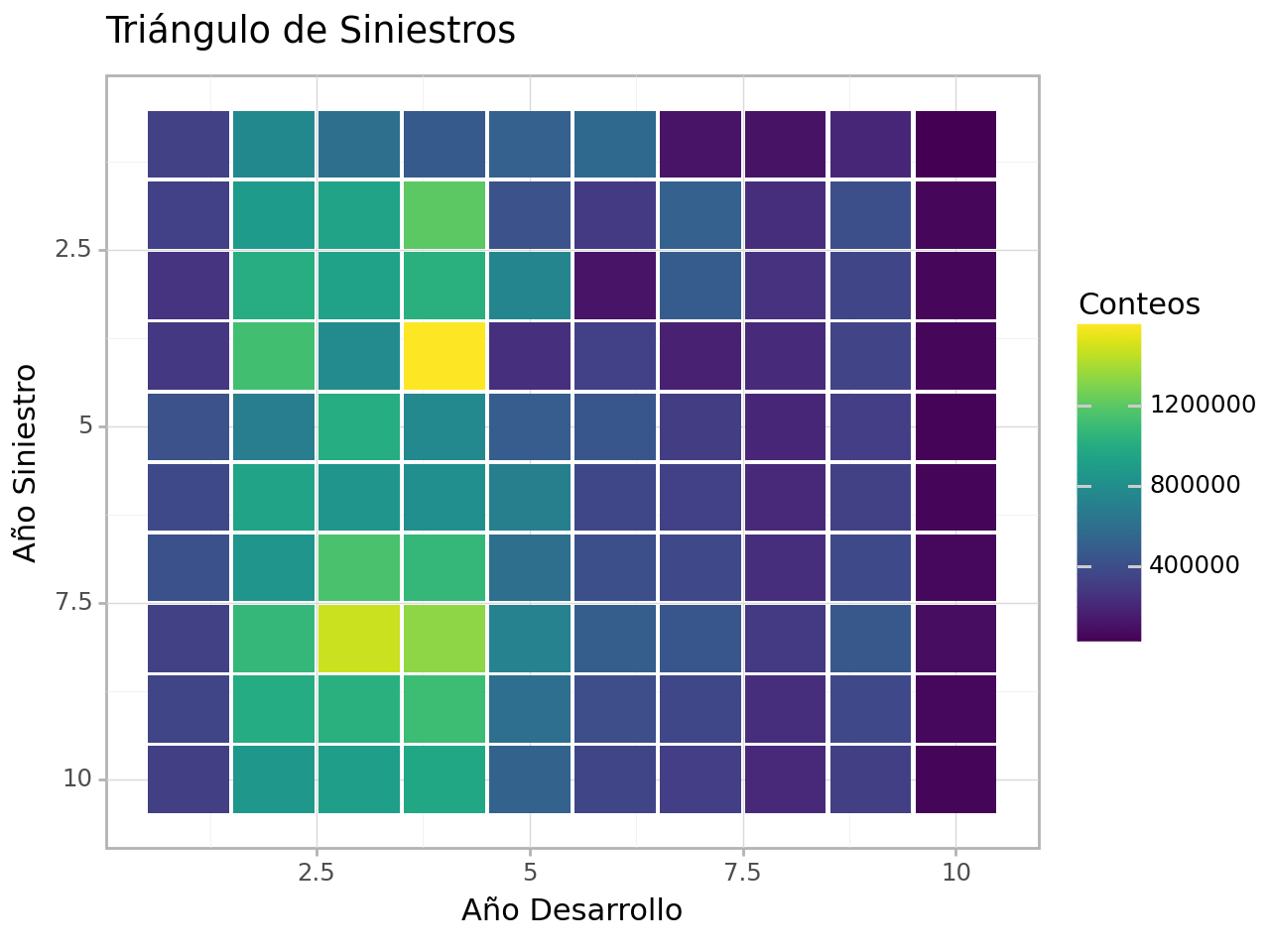
# Llenar triángulo con estimaciones
tr.fill()

Año Desarrollo      1        2        3        4       5       6       7   \
Año Siniestro                                                               
1               357848   766940   610542   482940  527326  574398  146342   
2               352118   884021   933894  1183289  445745  320996  527804   
3               290507  1001799   926219  1016654  750816  146923  495992   
4               310608  1108250   776189  1562400  272482  352053  206286   
5               443160   693190   991983   769488  504851  470639  334148   
6               396132   937085   847498   805037  705960  383286  351547   
7               440832   847631  1131398  1063269  605548  424500  389348   
8               359480  1061648  1443370  1310258  725788  508791  466659   
9               376686   986608  1018834  1089615  603568  423113  388076   
10              344014   856803   897409   959755  531635  372686  341825   

Año Desarrollo      8       9       10  
Año Siniestro                           
1               139950  227229   67948  
2               266172  425046   94633  
3               280405  375833   93677  
4               247189  370179   92268  
5               226674  339455   84610  
6               238477  357131   89016  
7               264120  395533   98588  
8               316565  474072  118164  
9               263257  394240   98265  
10              231882  347254   86554

tr.fill().heat_plot(solo_observado=False)

<Figure Size: (640 x 480)>

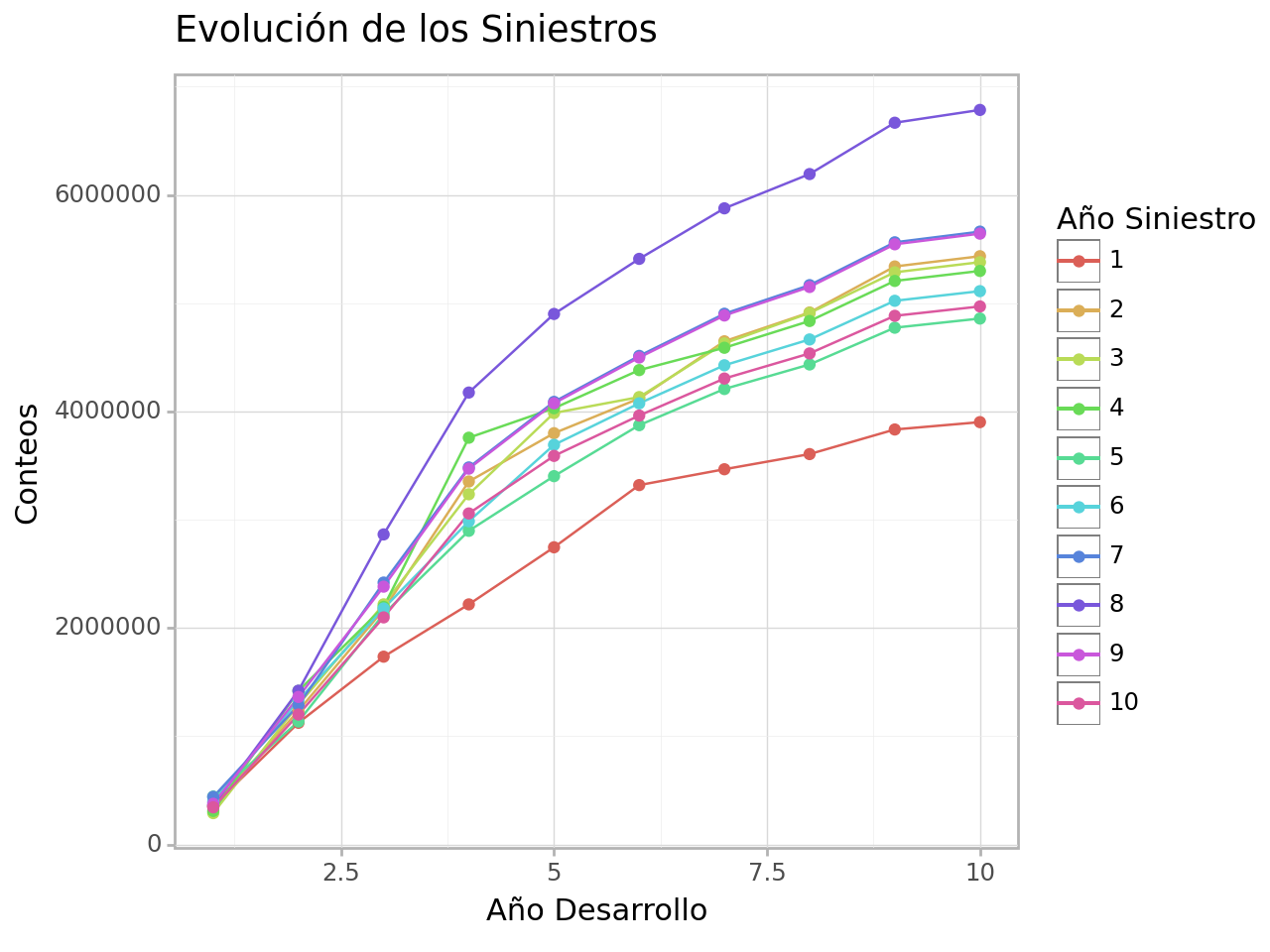
tr.fill().acumular(limpiar_tri_inferior=False).line_plot(solo_observado=False)

<Figure Size: (640 x 480)>

# Calcular estimación del total por año de desarrollo
tr.totales_año_siniestro()

Año Siniestro
1     3901463
2     5433718
3     5378825
4     5297904
5     4858198
6     5111169
7     5660767
8     6784795
9     5642262
10    4969817
Name: Conteos, dtype: int32

Métodos estocásticos

Mack

est_mack = tr.limite_superior_totales()
est_mack

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}

</style>

	Estimación Puntual	Error Estándar	Límite Superior
Año Siniestro
1	3901463	0	3.901463e+06
2	5433718	61420	5.534745e+06
3	5378825	108108	5.556647e+06
4	5297904	120710	5.496454e+06
5	4858198	252158	5.272961e+06
6	5111169	401095	5.770912e+06
7	5660767	546627	6.559888e+06
8	6784795	859056	8.197816e+06
9	5642262	958811	7.219366e+06
10	4969817	1352922	7.195176e+06
Total	53038918	2328132	5.686835e+07

Bootstrap

Paramétrico

# Residuales con distribución Normal
est_bt_par_norm = tr.bootstrap(parametrico=True,distribucion_parametrica='Normal')
est_bt_par_norm

[==================================================] 5000/5000

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}

</style>

	Estimación Puntual	Error Estándar	Límite Superior
Año Siniestro
1	3901463	1.184302e+06	7272655.20
2	5433718	1.194506e+06	7166172.85
3	5378825	1.057670e+06	6049189.10
4	5297904	1.095818e+06	6401729.95
5	4858198	1.327274e+06	8733218.40
6	5111169	1.230802e+06	7881980.60
7	5660767	1.234783e+06	8509389.20
8	6784795	1.053399e+06	6997681.90
9	5642262	9.765954e+05	7106063.70
10	4969817	4.144032e+05	5700470.50
Total	53038918	4.422593e+06	60836585.70

# Residuales con distribución t de Student
est_bt_par_t = tr.bootstrap(parametrico=True)
est_bt_par_t

[==================================================] 5000/5000

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}

</style>

	Estimación Puntual	Error Estándar	Límite Superior
Año Siniestro
1	3901463	1.225259e+06	7292054.55
2	5433718	1.195704e+06	7134433.85
3	5378825	1.080441e+06	6110840.05
4	5297904	1.134521e+06	6473687.75
5	4858198	1.349438e+06	8704490.00
6	5111169	1.248722e+06	7930195.05
7	5660767	1.306648e+06	8601035.45
8	6784795	1.075973e+06	7049736.35
9	5642262	1.014142e+06	7204075.65
10	4969817	4.213072e+05	5710403.80
Total	53038918	4.496274e+06	60942611.40

No paramétrico

# Función de distribución empírica
est_bt_npar = tr.bootstrap(suavizado=False)
est_bt_npar

[==================================================] 5000/5000

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}

</style>

	Estimación Puntual	Error Estándar	Límite Superior
Año Siniestro
1	3901463	1.194784e+06	7337137.20
2	5433718	1.167222e+06	7094851.55
3	5378825	1.046163e+06	6040221.35
4	5297904	1.085885e+06	6404389.35
5	4858198	1.303841e+06	8718231.95
6	5111169	1.205641e+06	7877555.95
7	5660767	1.226971e+06	8498999.25
8	6784795	1.037986e+06	7044096.35
9	5642262	9.747336e+05	7177121.70
10	4969817	3.998770e+05	5682028.40
Total	53038918	4.267568e+06	60639768.25

# Función de distribución empírica suavizada
est_bt_npar_suav = tr.bootstrap()
est_bt_npar_suav

[==================================================] 5000/5000

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}

</style>

	Estimación Puntual	Error Estándar	Límite Superior
Año Siniestro
1	3901463	1.369848e+06	7643879.20
2	5433718	1.317400e+06	7397655.10
3	5378825	1.208257e+06	6336944.45
4	5297904	1.237703e+06	6620871.75
5	4858198	1.491447e+06	9027322.25
6	5111169	1.357090e+06	8162928.95
7	5660767	1.414467e+06	8804822.10
8	6784795	1.185200e+06	7296835.30
9	5642262	1.128810e+06	7436971.40
10	4969817	4.651343e+05	5787567.65
Total	53038918	4.964007e+06	61766107.85

Exportar resultados

# Nombres abreviados de las metodologías
labs = ['Mack','BT P N', 'BT P T','BT NP','BT NP S']

with pd.ExcelWriter('resultado_comparación.xlsx') as writer:
    est_mack.to_excel(writer,sheet_name = labs[0])
    est_bt_par_norm.to_excel(writer,sheet_name = labs[1])
    est_bt_par_t.to_excel(writer,sheet_name = labs[2])
    est_bt_npar.to_excel(writer,sheet_name = labs[3])
    est_bt_npar_suav.to_excel(writer,sheet_name = labs[4])

Comparación de resultados

limites_superiores = {}
for lb in labs:
    limites_superiores[lb] = np.array(pd.read_excel('resultado_comparación.xlsx',
                                           sheet_name=lb)['Límite Superior'])
indices = pd.read_excel('resultado_comparación.xlsx',
                        sheet_name='Mack').set_index('Año Siniestro').index
df_limites = pd.DataFrame(limites_superiores,
                          index = indices).drop('Total')
df_limites

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}

</style>

	Mack	BT P N	BT P T	BT NP	BT NP S
Año Siniestro
1	3.901463e+06	7272655.20	7292054.55	7337137.20	7643879.20
2	5.534745e+06	7166172.85	7134433.85	7094851.55	7397655.10
3	5.556647e+06	6049189.10	6110840.05	6040221.35	6336944.45
4	5.496454e+06	6401729.95	6473687.75	6404389.35	6620871.75
5	5.272961e+06	8733218.40	8704490.00	8718231.95	9027322.25
6	5.770912e+06	7881980.60	7930195.05	7877555.95	8162928.95
7	6.559888e+06	8509389.20	8601035.45	8498999.25	8804822.10
8	8.197816e+06	6997681.90	7049736.35	7044096.35	7296835.30
9	7.219366e+06	7106063.70	7204075.65	7177121.70	7436971.40
10	7.195176e+06	5700470.50	5710403.80	5682028.40	5787567.65

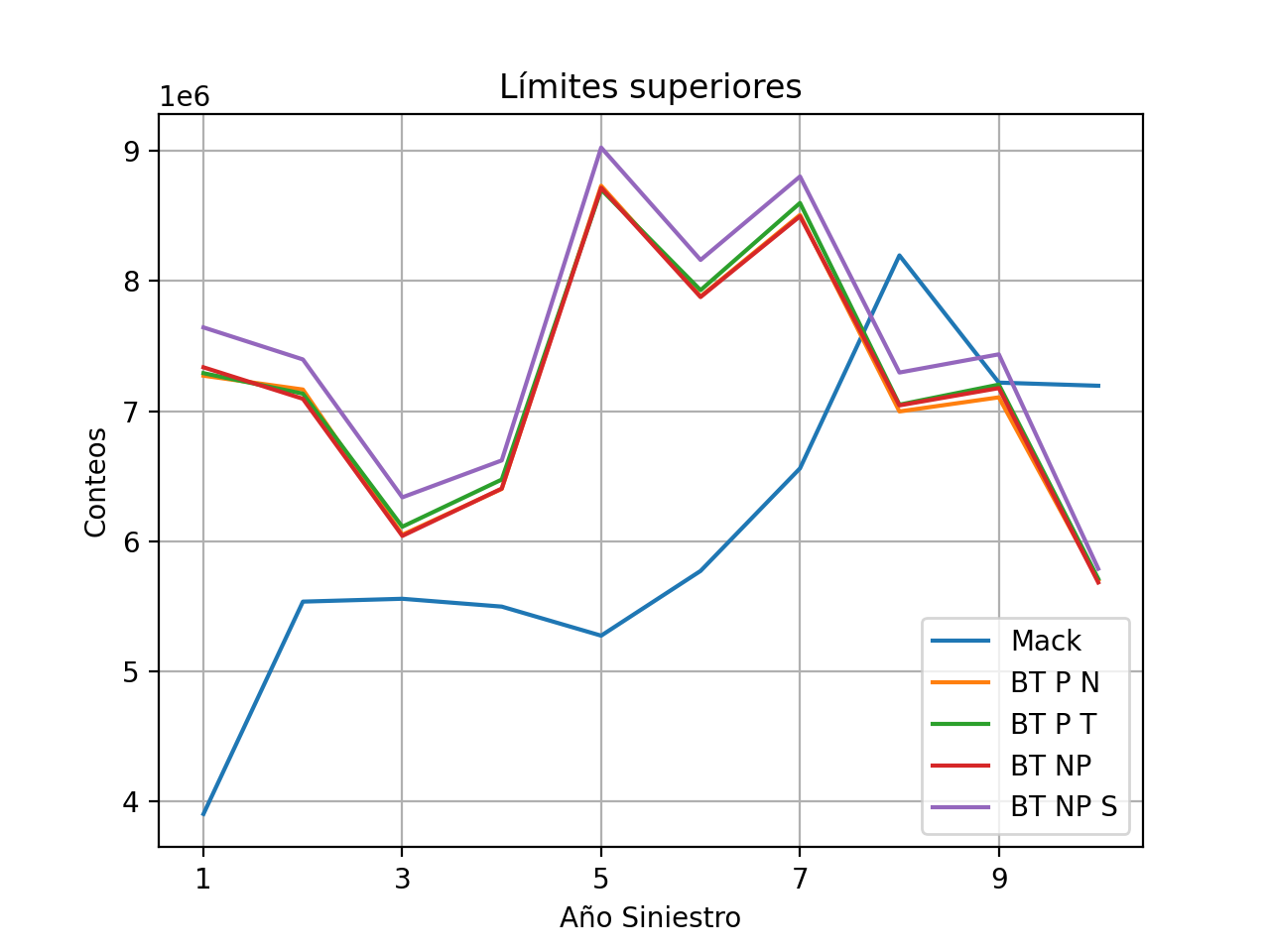
df_limites.plot(y = df_limites.columns,kind = 'line',
                title = 'Límites superiores',ylabel = tr.tipo)
plt.grid()
plt.show()

Reserva

tr.reserva(metodo = 'Mack')

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}

</style>

	Estimación Puntual	Error Estándar	Límite Superior
Año Siniestro
1	0	0	0.000000e+00
2	94633	61420	1.956599e+05
3	469510	108108	6.473318e+05
4	709636	120710	9.081863e+05
5	984887	252158	1.399650e+06
6	1419457	401095	2.079200e+06
7	2177637	546627	3.076758e+06
8	3920297	859056	5.333318e+06
9	4278968	958811	5.856072e+06
10	4625803	1352922	6.851162e+06
Total	18680828	2328132	2.251026e+07

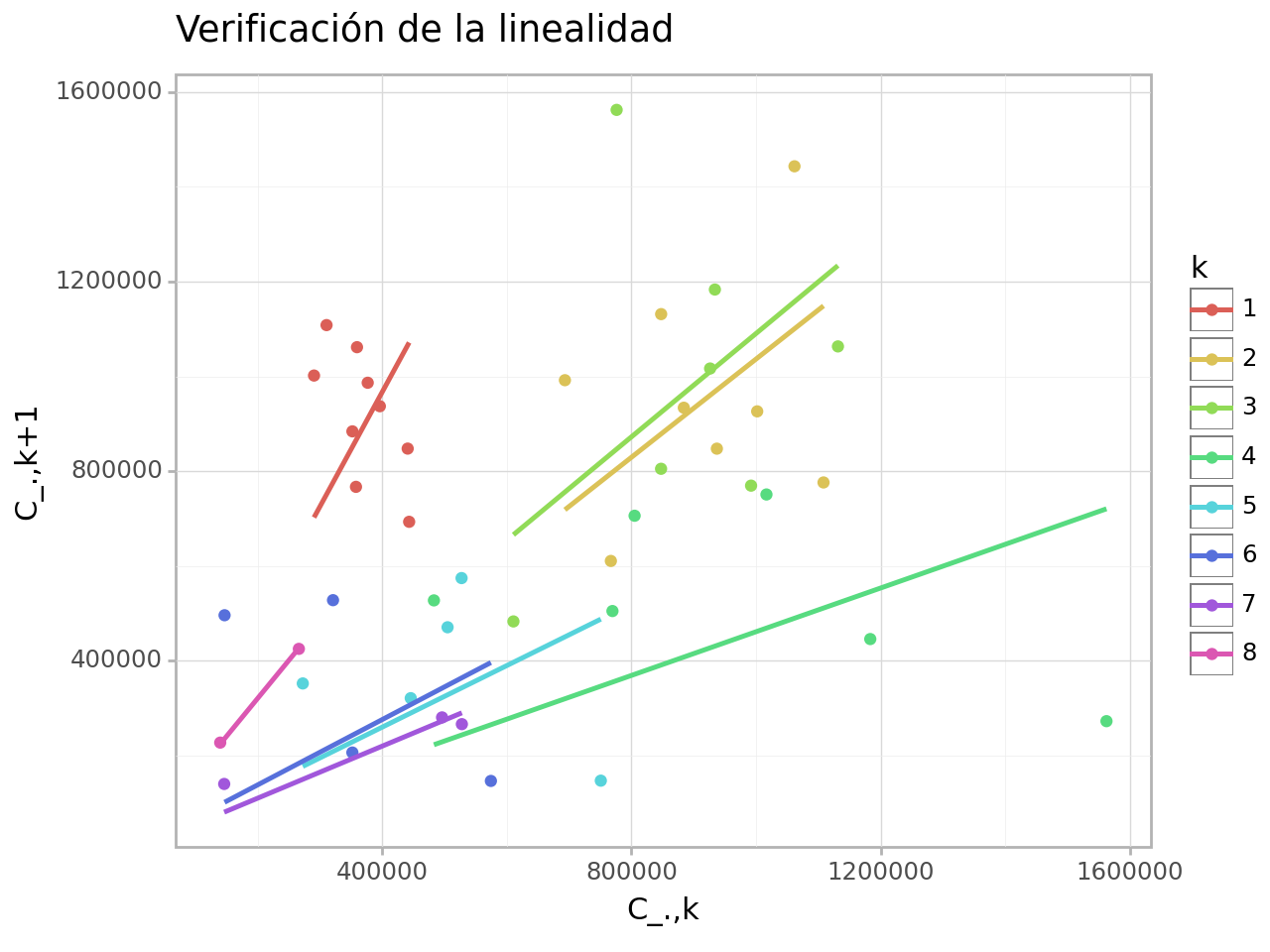
Revisión de residuales y supuestos

tr.grafico_linealidad()

<Figure Size: (640 x 480)>

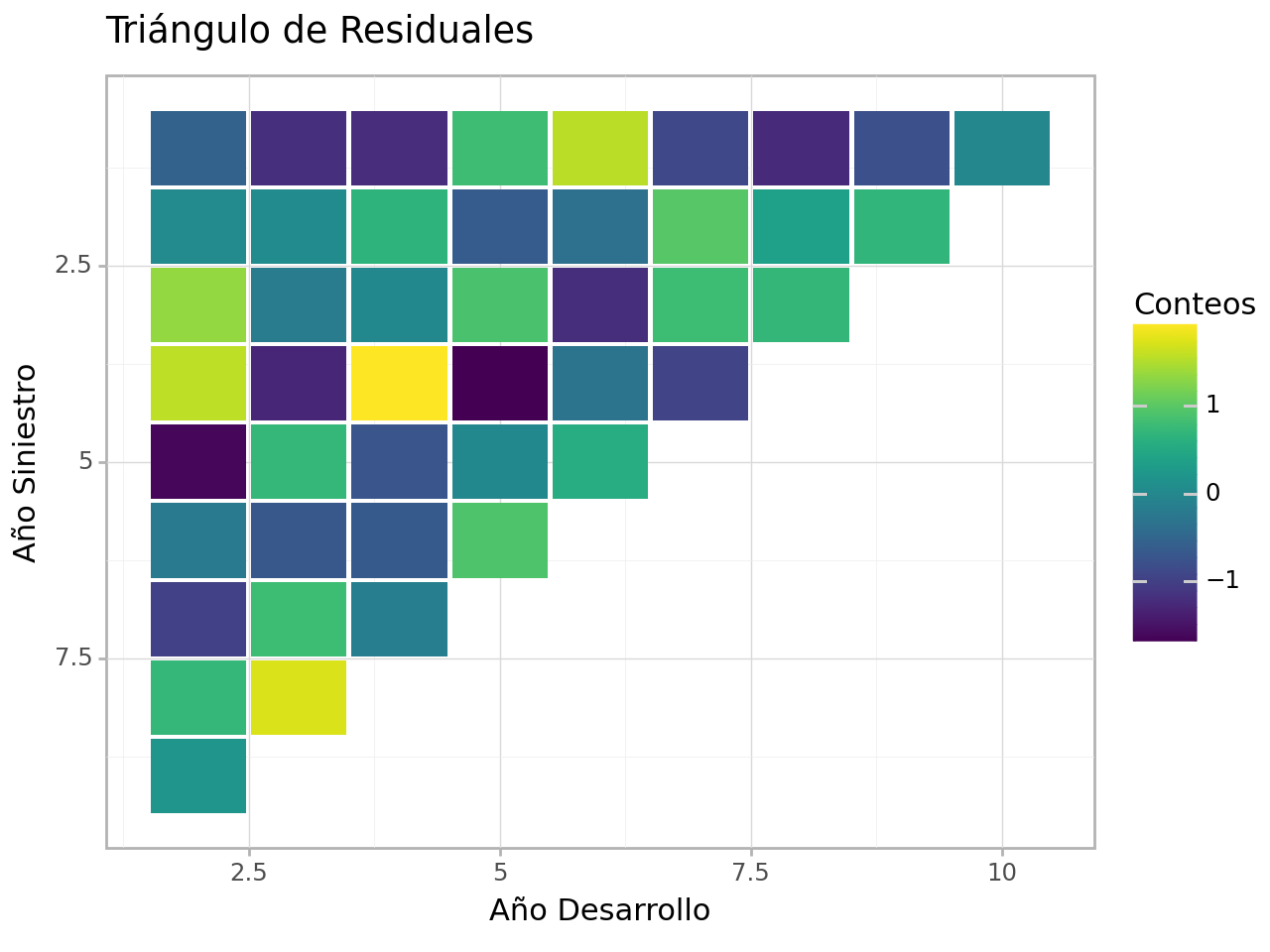
res_tr = tr.residuales(retornar_triangulo=True) # Calcular triángulo de residuales
res_tr.heat_plot(titulo = 'Triángulo de Residuales')

<Figure Size: (640 x 480)>

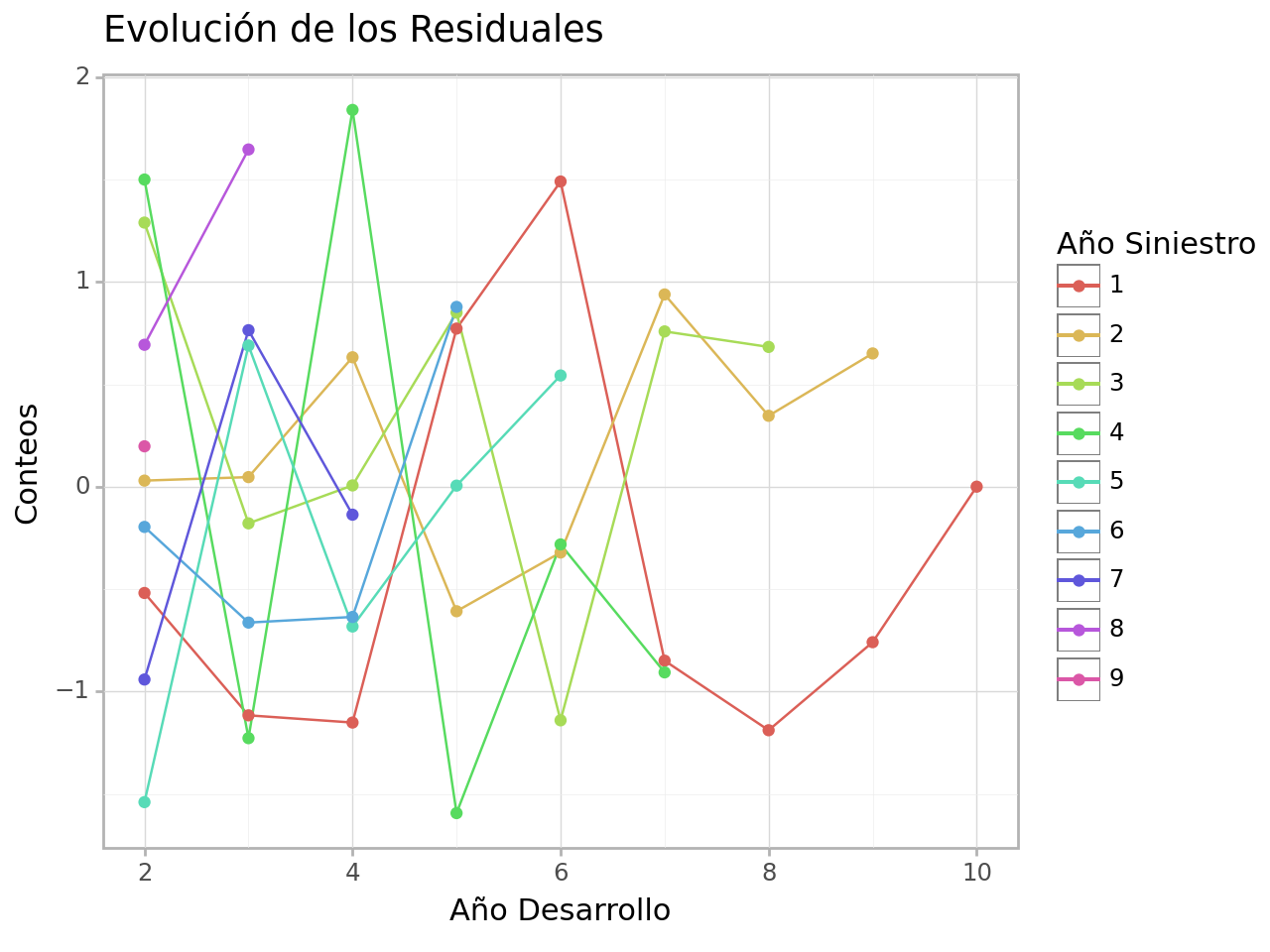
res_tr.line_plot(titulo = 'Evolución de los Residuales')

<Figure Size: (640 x 480)>

res = tr.residuales() # Extraer vector de residuales
# Graficar función de densidad
x_grid = np.linspace(-3.5,3.5,num = 500)
kde = st.gaussian_kde(res)
y_vals = kde(x_grid)
plt.plot(x_grid,y_vals,color = 'orange')
plt.fill_between(x_grid,y_vals,color = 'orange',alpha = 0.5)
plt.title('Estimación de la función de densidad de los residuales')
plt.ylabel('Densidad')
plt.grid()
plt.show()

# Prueba de normalidad
st.kstest(res,st.norm.cdf).pvalue

0.8092109489011762

# Otra prueba de normalidad
st.shapiro(res).pvalue

0.26435425877571106

# Prueba de distribución t
n_res = len(res)
n_par = 2*(len(tr.años_desarrollo) - 1)
st.kstest(res,lambda x: st.t.cdf(x,df = n_res - n_par)).pvalue

0.8355470703736473

Samuel-col/IBNR-python

Comparación de Métodos Estocásticos de estimación de IBNR

Carga de datos

Gráficos descriptivos

Chain-Ladder

Métodos estocásticos

Mack

Bootstrap

Paramétrico

No paramétrico

Exportar resultados

Comparación de resultados

Reserva

Revisión de residuales y supuestos