Diseño de Muestreo Óptimo

Esta función recibe un modelo de varigrama, un mapa (archivo .shp) y un conjunto de puntos en los que se quieren hacer predicciones y retorna los lugares en los que se deben tomar los registros para minimizar la varianza del error de predicción a través de kriging simple, ordinario o universal.

De acuerdo con Bohórquez (2022), un diseño óptimo $S_{n}^{*}$ se define como

$$S_{n}^{*}=\arg \max_{S_{n} \in \Xi_{n}} \Phi\left(\boldsymbol{\Theta}, S_{n}\right)$$

donde $\Phi\left(\boldsymbol{\Theta}, S_{n}\right)$ es el criterio de diseño y constituye cualquier medida escalar de información obtenida a partir de la configuración $S_{n}$ y que depende del vector de parámetros. Así, si se conoce el variograma de la variable de interés, entonces es posible optimizar el esquema de muestreo de modo que se minimice una función objetivo relacionada con el error de la predicción. En particular, la varianza del error de las predicciones en $m$ lugares no observados $S_{0}={s_{0}^{1}, ..., s_{0}^{m}}$ puede ser minimizada.

Kriging

El kriging espacial univariado puede ser de tres tipos: simple, ordinario y universal. Cada uno estima de forma distinta los coeficientes $\lambda$ que determinan la combinación lineal con la cual se va a predecir en un punto $s_0$ a partir de los puntos observados y, por lo tanto, cada uno tiene una expresión distinta para la varianza de su predicción.

Actualmente, esta función soporta kriging simple en términos de la covarianza, y kriging ordinario y universal en términos tanto de la covarianza como de la semivarianza. Se utilizan las siguientes fórmulas para la varianza de la predicción Cressie (1993):

En términos de la covarianza:

$$\sigma^2(s_0) = C(0) -2\lambda'c + \lambda'\Sigma\lambda$$

En términos de la semivarianza:

$$\sigma^2(s_0) = 2\lambda'\gamma - \lambda'\Gamma\lambda$$

donde:

$\sigma^2(s_0)$ es la varianza de predicción en el punto $s_0$.
$C(\cdot)$ es el modelo de covarianza.
$c$ es el vector de las covarianzas espaciales entre los puntos observados y $s_0$.
$\Sigma$ es la matriz de covarianzas espaciales entre los puntos observados.
$\gamma$ es el vector de semivarianzas espaciales entre los puntos observados y $s_0$.
$\Gamma$ es la matriz de semivarianzas espaciales entre los puntos observados.

Se busca entonces posicionar $k$ estaciones de tal manera que se minimice la varianza de predicción en los puntos pasados al argumento $s_0$. La minimización se hace con la función optim y el método L-BFGS-B con un máximo de 85 iteraciones que casi siempre resulta ser más que suficiente.

optimal_design <- function(k, s0, vgm_model = NULL,cov_model = NULL, 
                           krigingType = "simple",range = NULL,
                           psill = NULL, nugget = 0,
                           krig_formula = NULL,grid = NULL,map = NULL,
                           plt = T,...){

Dependencias

gstat (Sólo si se van a usar sus modelos de semivariograma).
ggplot2
sf
sp

Todos estos paquetes están disponibles en CRAN.

Argumentos

Argumento	Descripción
`k`	Número de estaciones a ubicar
`S0`	Objeto de tipo `matrix` o `data.frame` que contenga las coordenadas de las ubicaciones de interés (donde se desean hacer predicciones)
`vgm_model`	Objetode tipo `variogramModel` del paquete gstat que representa el modelo de semivarianza.
`cov_model`	Función que define un modelo de covarianza especificado por el usuario. Esta será utilizada si no se suministra el argumento `vgm_model`. Si se pasa este argumento, también se deben pasar los argumentos `range` y `psill`. Además, todos los argumentos adicionales que se pasen a la función `optimal_design` serán pasados a la función `cov_model`. Esto es útil cuando se tienen parámetros adicionales como `kappa` en el modelo Matern.
`krigingType`	Tipo de kriging a utilizar, e.g. "simple", "ordinary" o "universal".
`range`	Rango del modelo `cov_model`.
`psill`	Silla del modelo `cov_model`.
`nugget`	Pepita del modelo `cov_model`. Por defecto es cero.
`krig_formula`	Fórmula que define la variable dependiente como un modelo lineal de variables independientes, e.g. "x+y". Sólo se utiliza en el kriging universal. Es un objeto de tipo string que sólo contiene la parte independiente de la fórmula, es decir, en vez de "z ~ x + y" se debe suministrar "x + y".
`grid`	Objeto de tipo matrix o data.frame. Grilla de puntos en los cuales se pueden ubicar estaciones.
`map`	Objeto de tipo SpatialPolygonsDataFrame que limita el área geográfica donde las estaciones quieren ser ubicadas si no se pasa ningún objeto en el argumento `grid`.
`plt`	Booleano que determina se se debe generar un gráfico con el resultado obtenido o no.
`...`	Argumentos adicionales que se pasarán a la función `cov_model`.

Valor

Una lista con los siguientes objetos

Objeto	Descripción
`coords`	Objeto de tipo `matrix` y `array` que contiene las coordenadas óptimas para las estaciones.
`plot`	Gráfico del paquete `ggplot2` que presenta el resultado. En él, los puntos grises representan la grilla de puntos en la que se podían situar las estaciones.

Detalles

Ejemplo

Cargamos la librerías y scripts necesarios.

library(gstat)
library(rgdal)
library(ggplot2)
library(sf)
library(sp)

source("../src/optimal_design.r")
source("../src/gstat_model.r")
source("../src/own_model.r")

Ahora, cargamos el mapa y creamos el modelo de semivariograma con los cuales trabajaremos.

mapa <- rgdal::readOGR(dsn = "../data/Boyacá.shp")

modelo_svg <- vgm(psill = 5.665312,
                  model = "Exc",
                  range = 88033.33,
                  kappa = 1.62,
                  add.to = vgm(psill = 0.893,
                               model = "Nug",
                               range = 0,
                               kappa = 0))

my.CRS <- sp::CRS("+init=epsg:21899") # https://epsg.io/21899


mapa <- spTransform(mapa,my.CRS)

Ya podemos crear un conjunto de puntos en el mapa en los cuales queremos predecir de manera óptima y llamar a la función optimal_design.

target <- sp::spsample(mapa,n = 100, type = "random") # Puntos sobre los que queremos realizar una predicción de varianza mínima.

optimal_design(k = 10, s0 = target,vgm_model = modelo_svg,
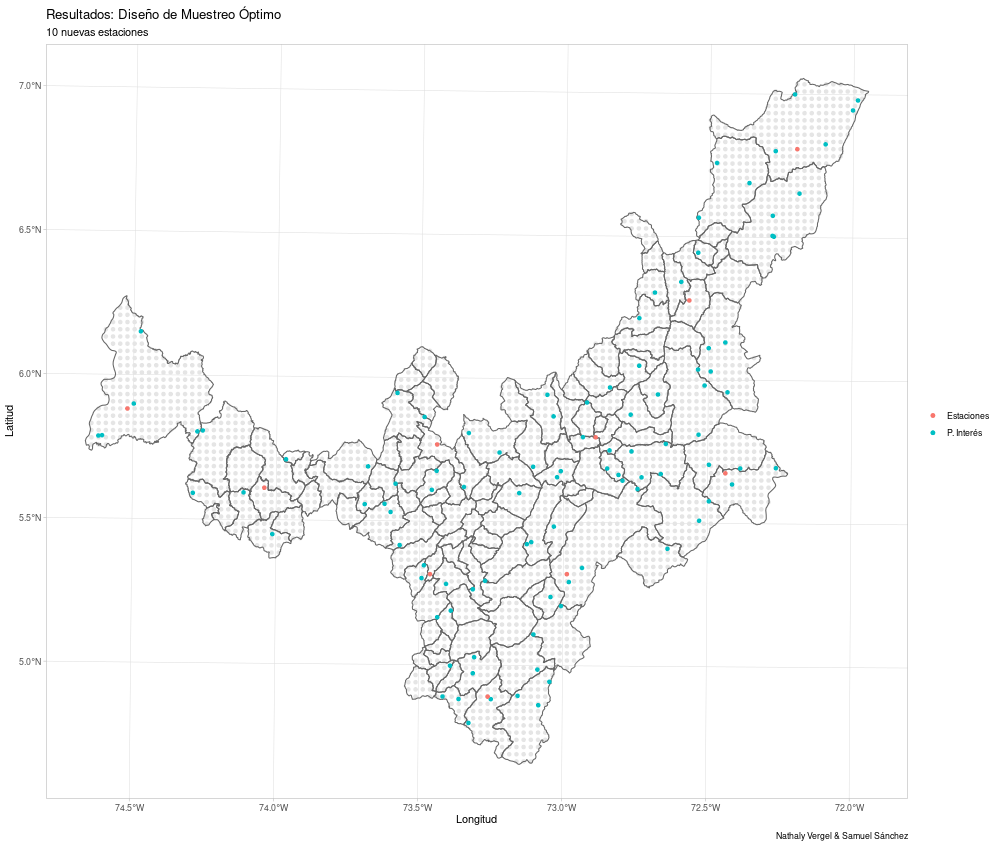
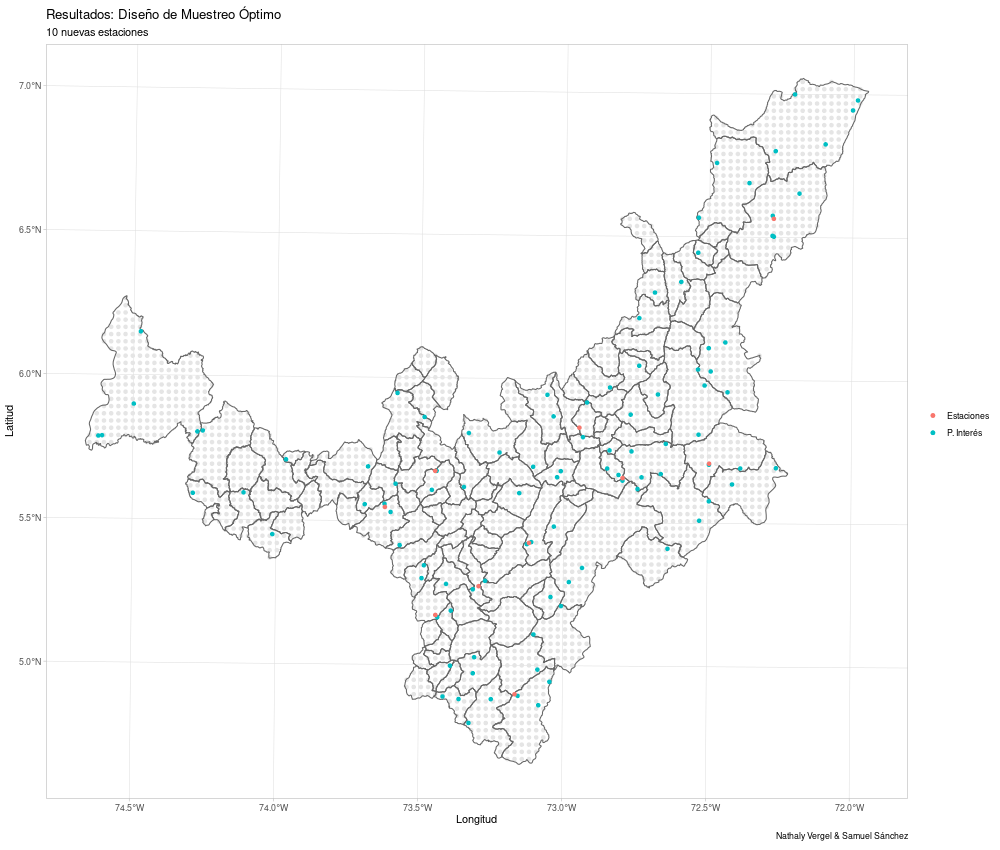
               krigingType = "simple",map = mapa) -> res1

res1

Las coordenadas óptimas son

##      x1       x2
## [1,] 516425.7 1121174
## [2,] 455101.3 1082149
## [3,] 404926.9 1132324
## [4,] 502488.3 1188073
## [5,] 544300.3 1246610
## [6,] 466251.2 1135111
## [7,] 424439.2 1034762
## [8,] 285065.7 1146261
## [9,] 338027.7 1115599
## [10,] 402139.4 1082149

El gráfico se muestra a continuación. Los puntos grises representan la grilla de puntos en los que se podían ubicar las estaciones.

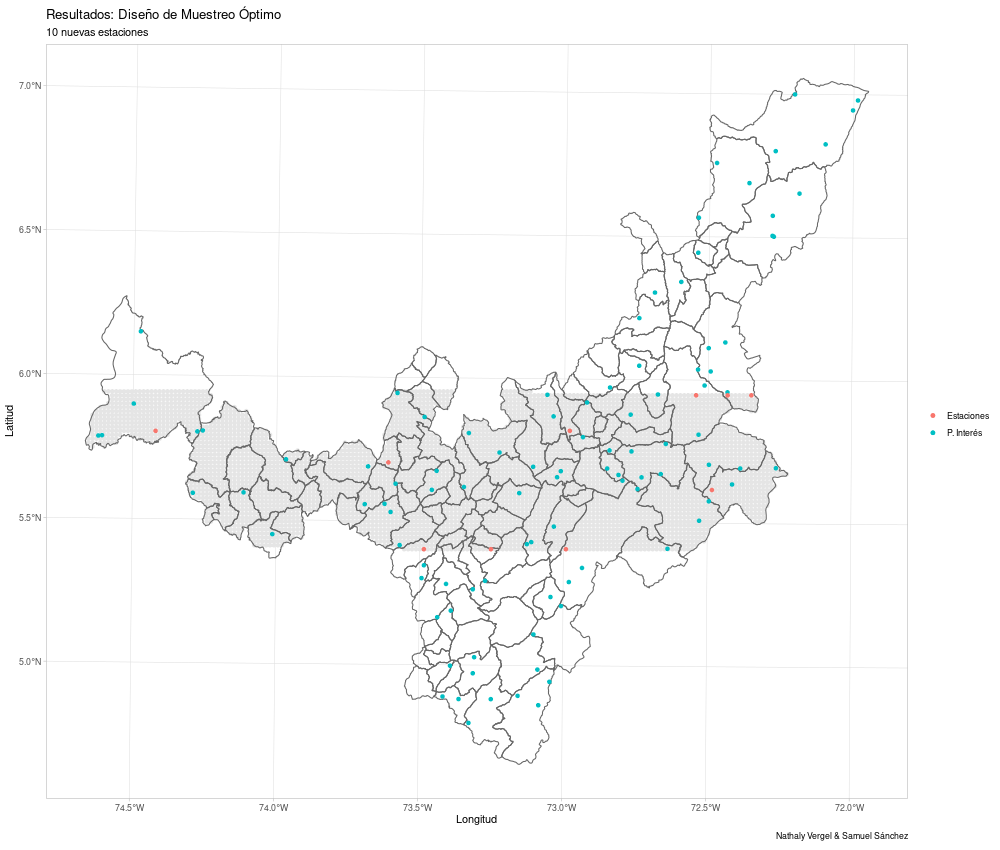
A continuación se muestran otros ejemplos para kriging ordinario y kriging universal suministrando una grilla específica de puntos en los que se pueden ubicar las estaciones y un modelo de semivarianza del paquete gstat.

mi.grilla <- sp::spsample(mapa,n=1e4,type = "regular")
mi.grilla <- mi.grilla[2e3:7e3]                          


optimal_design(k=10,s0 = target,model = modelo_svg,
               krigingType = "ordinary",
               grid = as.data.frame(mi.grilla)) -> res2

res2


optimal_design(k = 10, s0 = target, model = modelo_svg,
               krigingType = "universal", form = "x + I(x^2) + y",
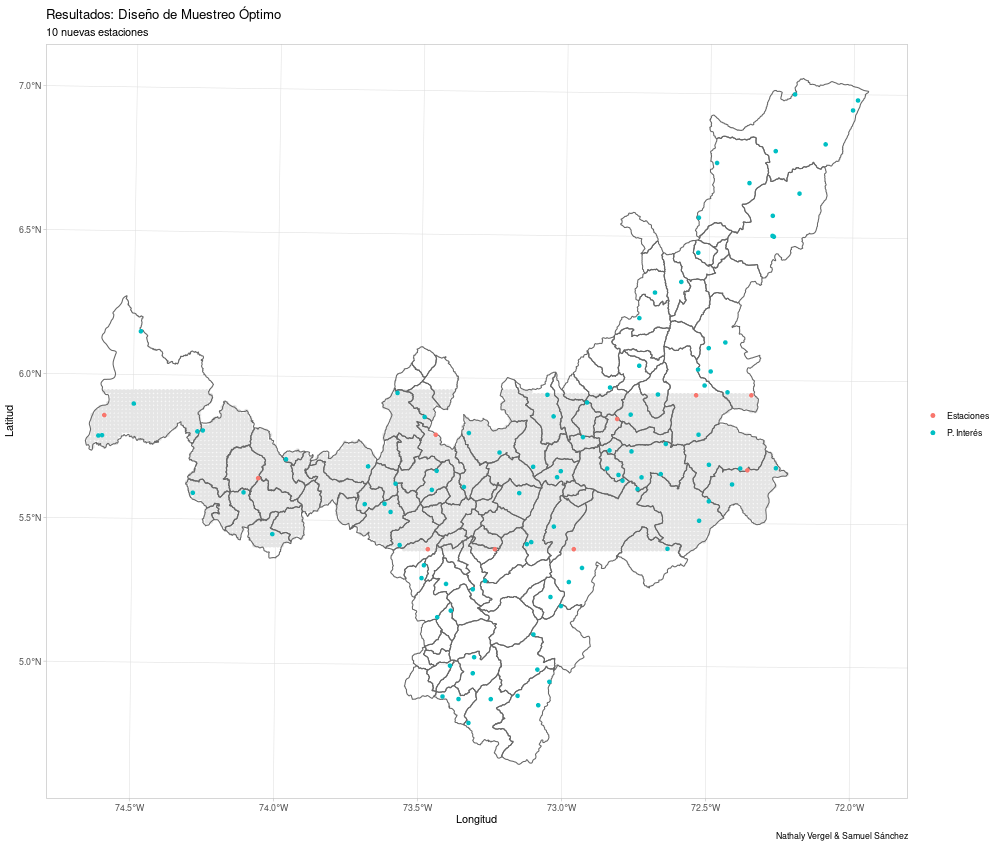
               grid = as.data.frame(mi.grilla)) -> res3

res3

Ahora presentaremos cuatro ejemplos suministrando un modelo de covarianza definido manualmentes y los distintos tipos de kriging.

my_cov_model <- function(h, range, psill, nugget = 0){
  ifelse(h == 0,
         nugget + psill,
         ifelse(h > 0,
                psill*(exp((-1)*h/range)),
                "Las distancias deben ser positivas"
         )
  )
}

# Parámetros
my_range = 20000
my_psill = 5
my_nugget = 1

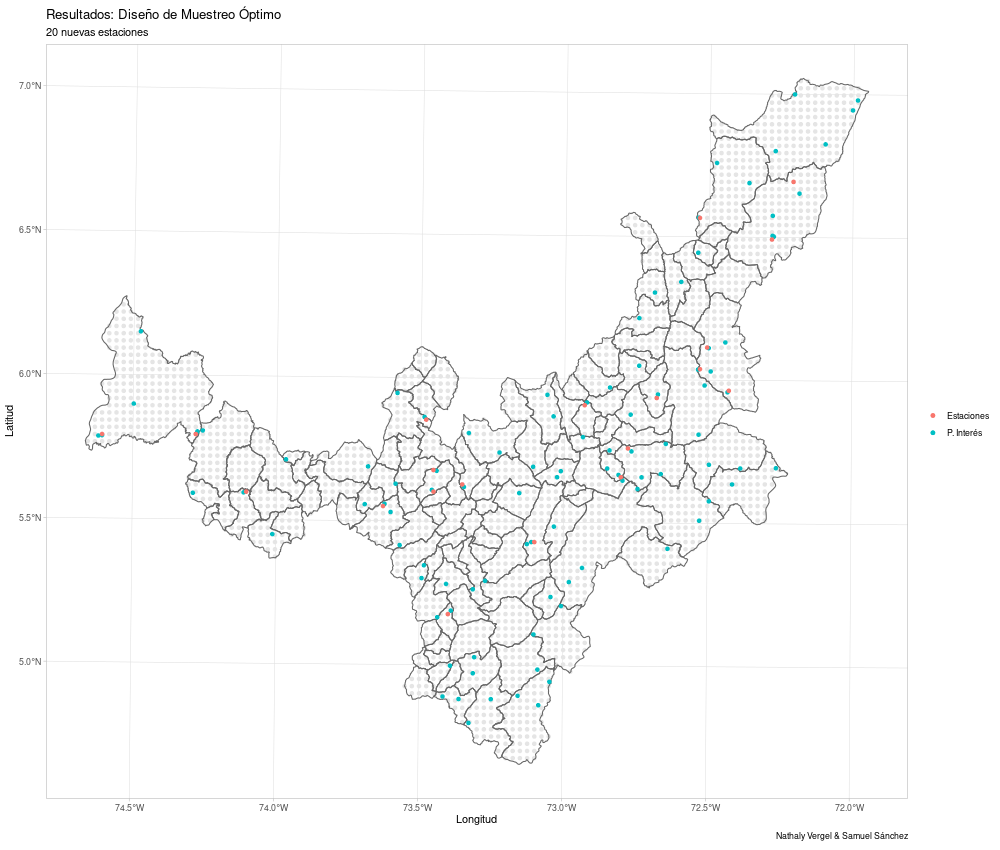
Se llama a la función optimal_design cuatro veces

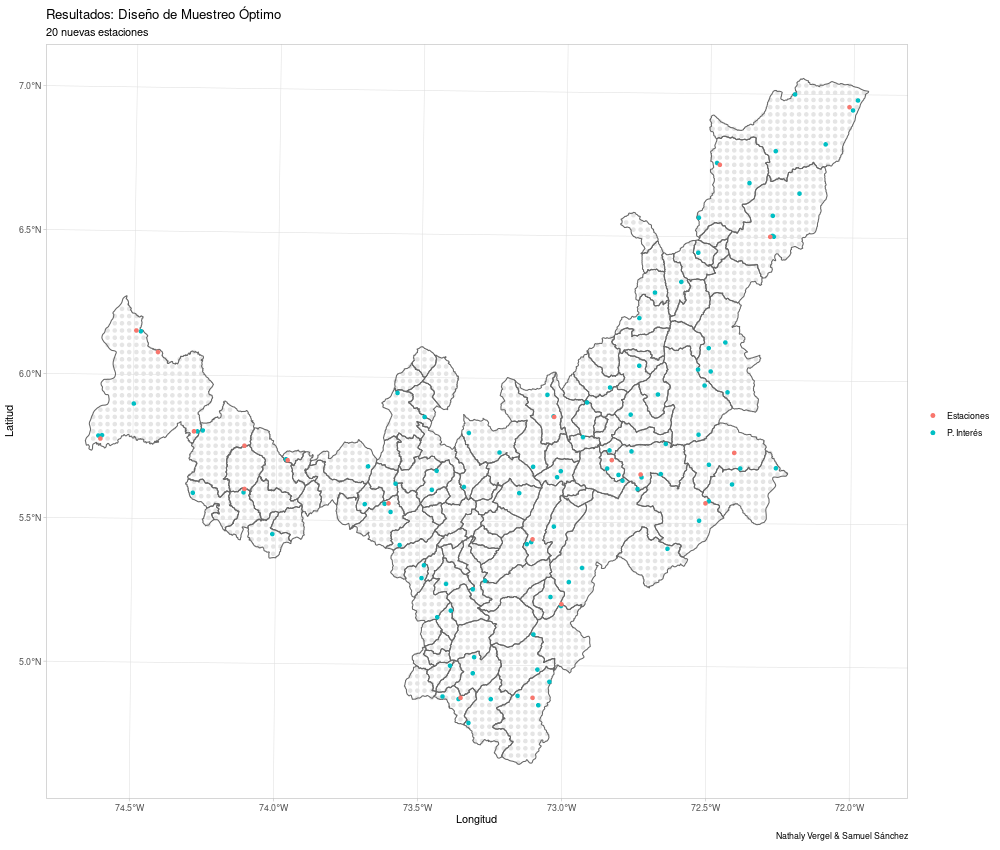
optimal_design(k = 20, s0 = as.data.frame(target), cov_model = my_cov_model,
               krigingType = "simple",map = mapa,
               range = my_range, psill = my_psill,
               nugget = my_nugget) -> res4

res4


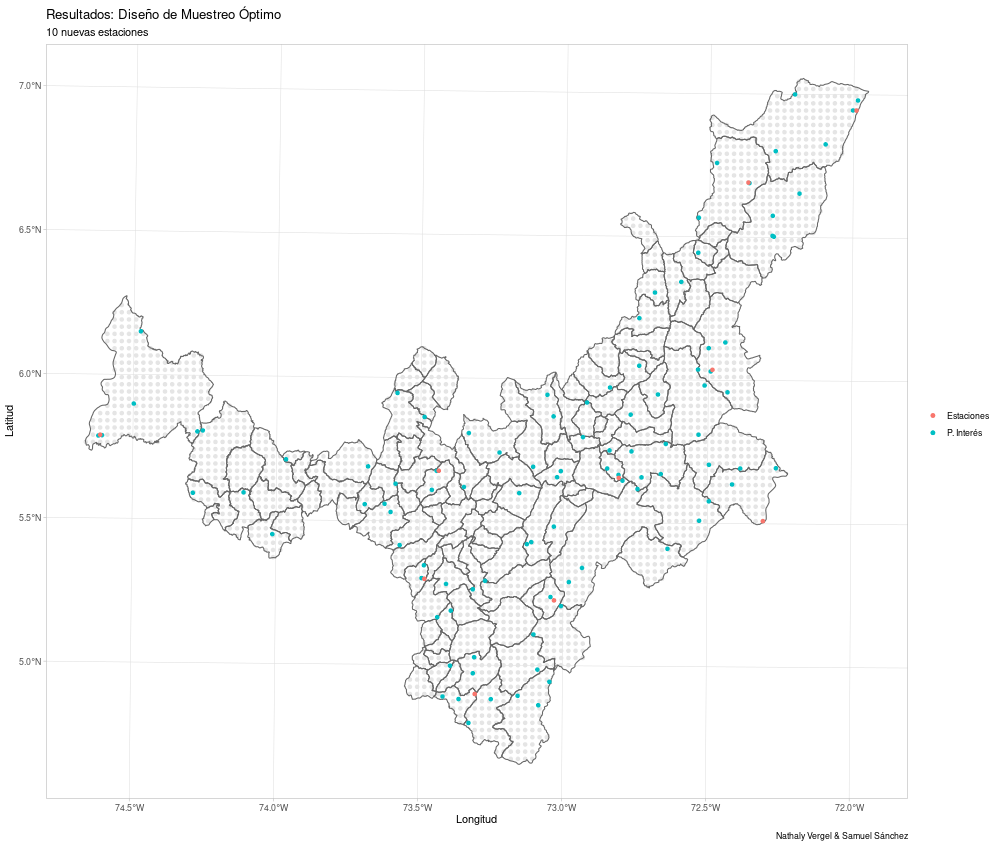
optimal_design(k = 10, s0 = as.data.frame(target), cov_model = my_cov_model,
               krigingType = "ordinary",map = mapa,
               range = my_range, psill = my_psill,
               nugget = my_nugget) -> res5

res5


optimal_design(k = 20, s0 = as.data.frame(target), cov_model = my_cov_model,
               krigingType = "universal",map = mapa,
               range = my_range, psill = my_psill,
               nugget = my_nugget,krig_formula = "x + y") -> res6

res6


optimal_design(k = 10, s0 = as.data.frame(target), cov_model = my_cov_model,
               krigingType = "universal",map = mapa,
               range = my_range, psill = my_psill,
               nugget = my_nugget,krig_formula = "x + sqrt(y)") -> res7

res7

Y se obtienen los respectivos resultados:

Referencias

Bohorquez, M. (2022). Estadística Espacial Espacio-Temporal para Campos Aleatorios Escalares y Funcionales. [Notas de Clase].
Cressie, N. (1993). Statistics for Spatial Data. John Wiley & Sons. Inc.

Creado por:

Nathaly Vergel (nvergel@unal.edu.co)
Samuel Sánchez (ssanchezgu@unal.edu.co)

Samuel-col/optimalSpatialDesign