Web app presenting some insights about the constant elasticity of substitution function.
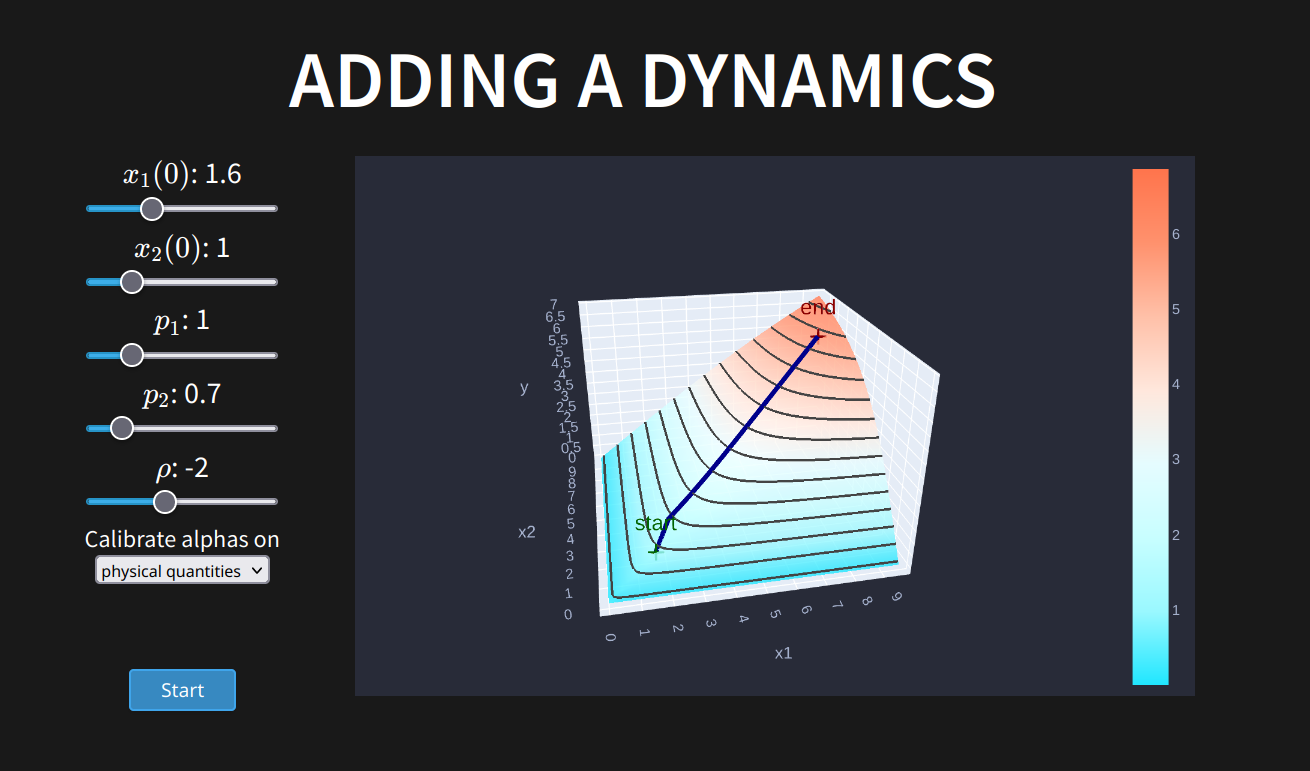
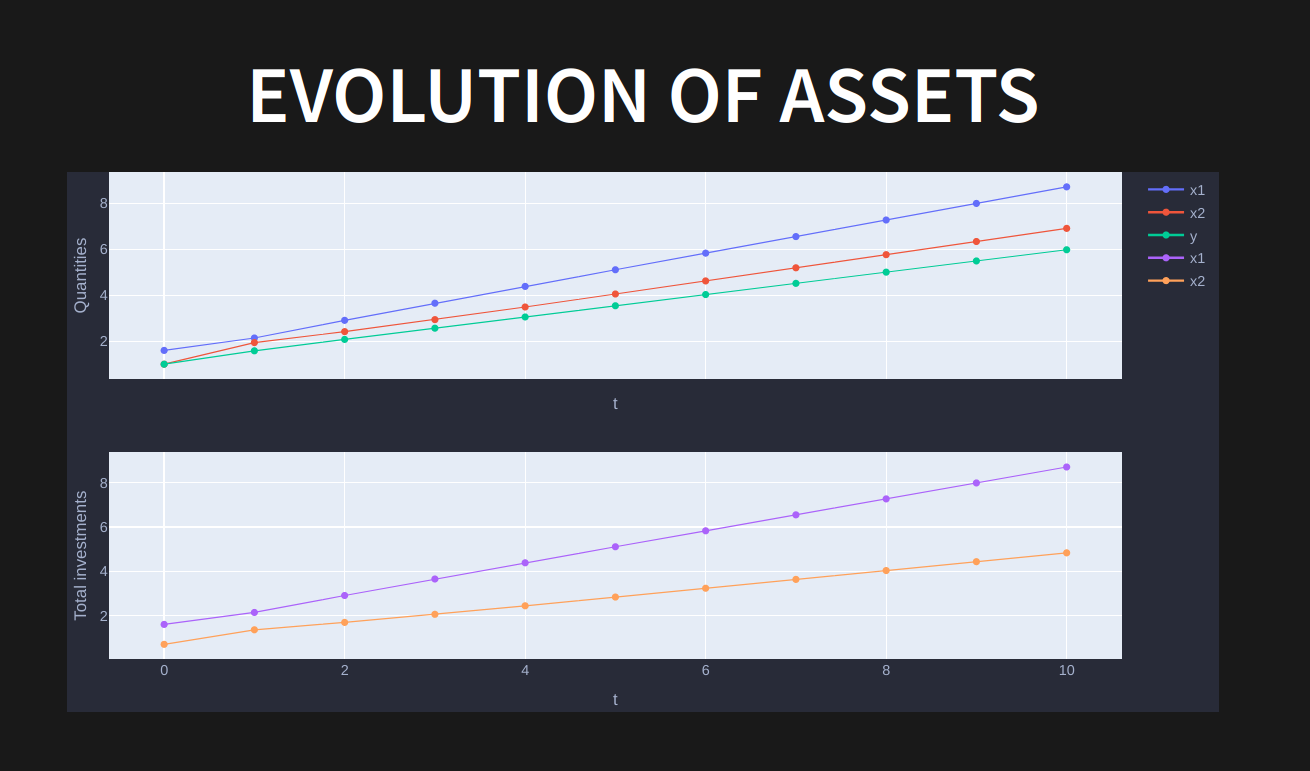
We first propose some plots of the function with intercative sliders. In a second part, we design and solve an optimal control problem consisting in maximizing a CES under a constraint on total investments.
This app is codes in Python (Flask), HTML, CSS and javascript. I used the Javascript framework Reveal.js that allows to build presentations with web languages.
First, pip install the requirements.txt. Then type the following line in your terminal
cd src
python flask_app.py